10.4 Test de Kruskal-Wallis

Les conditions d’application de l’ANOVA sont assez restrictives, en particuliers l’homoscédasticité et le normalité des résidus. Dans notre example, nous avons pu stabiliser la variance par une transformation puissance cinq, mais la distribution des résidus n’est pas optimale. Nous pouvons tout aussi bien décider de nous orienter vers la version non paramétrique équivalente : le test de Kruskal-Wallis.

Le raisonnement entre ANOVA (test paramétrique) et Kruska-Wallis (test non paramétrique) est le même qu’entre le test de Student ou celui de Wilcoxon. Lorsque les conditions sont remplies, l’ANOVA est un test plus puissant à utiliser en priorité. Nous le préfèrerons donc, sauf dans les cas impossibles où aucune transformation des données ne permet d’obtenir une distribution acceptable des résidus et des variances.

Le test de Kruskal-Wallis va comparer la localisation des points sur l’axe plutôt que les moyennes. Nous travaillons ici sur les rangs. La transformation en rangs consiste à ranger les observations de la plus petite à la plus grande et à remplacer les valeurs par leur position (leur rang) dans ce classement. Les ex-aequos reçoivent des rangs équivalents. Un petit exemple :

# Un échantillon
x <- c(4.5, 2.1, 0.5, 2.4, 2.1, 3.5)
# Tri par ordre croissant
sort(x)

# [1] 0.5 2.1 2.1 2.4 3.5 4.5

# Remplacement par les rangs
rank(sort(x))

# [1] 1.0 2.5 2.5 4.0 5.0 6.0

Donc 0,5 donne 1, 2,1 apparait deux fois en position 2 et 3, donc on leurs attribue à tous les deux le rang 2,5. 2,4 est remplacé par 4, 3,5 par 5 et enfin 4,5 est remplacé par 6.

Dans le test de Kruskal-Wallis, sous \(H_0\) nous avons le même rang moyen (noté \(mr\)) pour chaque groupe parmi \(k\). Sous \(H_1\), au moins deux groupes ont des rangs moyens différents.

\(H_0:mr_1 = mr_2 = ... = mr_k\)
\(H_1: \exists(i, j) \mathrm{\ tel\ que\ } mr_i \neq mr_j\)

Nous ne détaillons pas les calculs (mais voyez ici). Le calcul aboutit en fait à une valeur de \(\chi^2_{obs}\) à \(k - 1\) degrés de liberté lorsque k populations sont comparées. Ainsi, nous avons déjà un loi de distribution théorique pour le calcul de la valeur P. La zone de rejet est située à la droite de la distribution comme dans le cas de l’ANOVA et du test de \(\chi^2\).

Le test est réalisé dans R avec la fonction kruskal.test(). Notez que les arguments sont les mêmes que pour l’ANOVA à un facteur. Un “snippet” est disponible dans la SciViews Box (.hn pour hypothesis tests: nonparametric, ensuite Kruskal-Wallis test).

kruskal.test(data = crabs2, aspect ~ group)

# 
#   Kruskal-Wallis rank sum test
# 
# data:  aspect by group
# Kruskal-Wallis chi-squared = 139.68, df = 3, p-value < 2.2e-16

Ici, nous rejettons \(H_0\) au seuil \(\alpha\) de 5%. Nous pouvons dire qu’il y a au moins une différence significative entre les ratios au seuil \(\alpha\) de 5% (test Kruskal-Wallis, \(\chi^2\) = 140, ddl = 3, valeur P << 10^-3).

Conditions d’application

Le test de Kruskal-Wallis est naturellement moins contraignant que l’ANOVA.

échantillon représentatif (par exemple, aléatoire),
observations indépendantes,
variable dite réponse quantitative,
une variable dite explicative qualitative à trois niveaux ou plus,
les distributions au sein des différentes sous-population sont, si possible, similaires mais de forme quelconque.

10.4.1 Test “post hoc” non paramétrique

Nous devrions également réaliser des tests “pot hoc” lorsque nous rejettons \(H_0\) du Kruskal-Wallis. Les version non paramétriques des tests de comparaisons multiples sont moins connus. Nous pourrions effectuer des comparaisons deux à deux avec des tests de Wilcoxon en appliquant une correction de Bonferroni.

Une autre option consiste à utiliser une version non paramétrique du test de Tukey basée sur les rangs, dit test pot hoc non paramétrique asymptotique. Les explications assez techniques sont disponibles ici. Ce test est également disponible dans la SciViews Box depuis .hn, en sélectionnant l’entrée Kruskal-Wallis: multiple comparisons dans le menu déroulant.

summary(kw_comp. <- nparcomp::nparcomp(data = crabs2, aspect ~ group))

# 
#  #------Nonparametric Multiple Comparisons for relative contrast effects-----# 
#  
#  - Alternative Hypothesis:  True relative contrast effect p is less or equal than 1/2 
#  - Type of Contrast : Tukey 
#  - Confidence level: 95 % 
#  - Method = Logit - Transformation 
#  - Estimation Method: Pairwise rankings 
#  
#  #---------------------------Interpretation----------------------------------# 
#  p(a,b) > 1/2 : b tends to be larger than a 
#  #---------------------------------------------------------------------------# 
#  
# 
#  #------------Nonparametric Multiple Comparisons for relative contrast effects----------# 
#  
#  - Alternative Hypothesis:  True relative contrast effect p is less or equal than 1/2 
#  - Estimation Method: Global Pseudo ranks 
#  - Type of Contrast : Tukey 
#  - Confidence Level: 95 % 
#  - Method = Logit - Transformation 
#  
#  - Estimation Method: Pairwise rankings 
#  
#  #---------------------------Interpretation--------------------------------------------# 
#  p(a,b) > 1/2 : b tends to be larger than a 
#  #-------------------------------------------------------------------------------------# 
#  
#  #----Data Info-------------------------------------------------------------------------# 
#   Sample Size
# 1    B-F   50
# 2    B-M   50
# 3    O-F   50
# 4    O-M   50
# 
#  #----Contrast--------------------------------------------------------------------------# 
#           B-F B-M O-F O-M
# B-M - B-F  -1   1   0   0
# O-F - B-F  -1   0   1   0
# O-M - B-F  -1   0   0   1
# O-F - B-M   0  -1   1   0
# O-M - B-M   0  -1   0   1
# O-M - O-F   0   0  -1   1
# 
#  #----Analysis--------------------------------------------------------------------------# 
#       Comparison Estimator Lower Upper Statistic      p.Value
# 1 p( B-F , B-M )     0.017 0.004 0.070 -7.229567 1.618261e-12
# 2 p( B-F , O-F )     0.695 0.542 0.815  3.257267 5.905270e-03
# 3 p( B-F , O-M )     0.051 0.018 0.137 -7.014700 7.867484e-12
# 4 p( B-M , O-F )     0.990 0.949 0.998  7.210499 2.279288e-12
# 5 p( B-M , O-M )     0.654 0.501 0.781  2.606445 4.792701e-02
# 6 p( O-F , O-M )     0.027 0.008 0.088 -7.385440 4.057865e-13
# 
#  #----Overall---------------------------------------------------------------------------# 
#   Quantile      p.Value
# 1 2.593391 4.057865e-13
# 
#  #--------------------------------------------------------------------------------------#

plot(kw_comp.)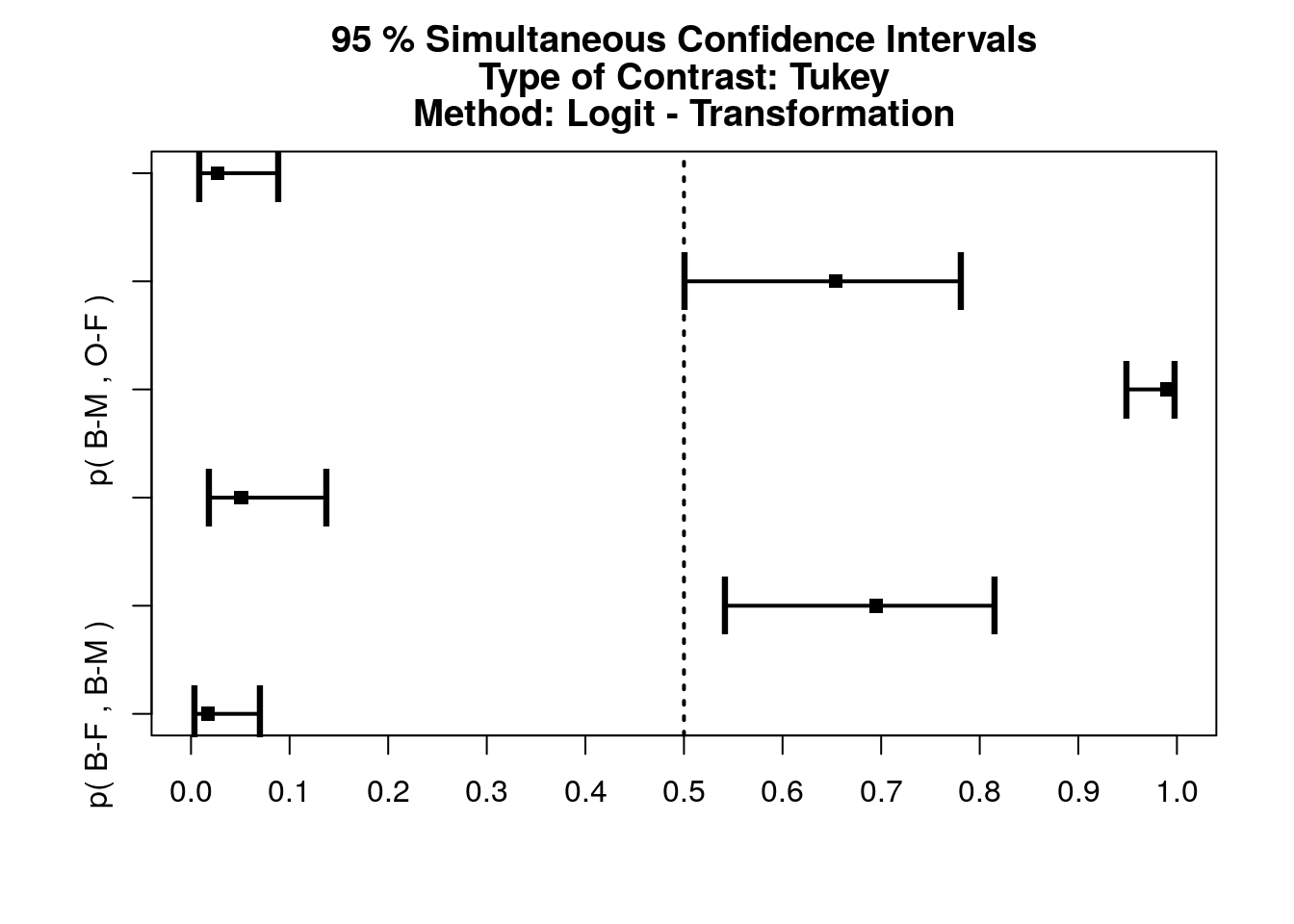

La présentation des résultats est plus détaillée que pour le HSD de Tukey. Le graphique est très imilaire. Ici, toutes les différences sont considérées comme significatives, même si la comparaison des mâles B-M - O-M avec une valeur P tout juste significative de 0,049 est à prendre avec des pincettes étant donné sa proximité du seuil.

Au final que conclure ? Lorsque l’ANOVA peut être utilisée, elle est à préférer. Ici avec une transformation puissance cinq, nous stabilisons la variance qui est le critère le plus sensible. De plus tant avec l’ANOVA qu’avec le Kruskal-Wallis, nous détectons des différences significatives. Les tests “post hoc” nous indiquent des différences significatives au seuil \(\alpha\) de 5% sauf peut-être pour les mâles (il faudrait prévoir des mesures supplémentaires pour confirmer ou infirmer à ce niveau).

A vous de jouer

Afin d’appliquer directement les concepts vu au cours dans ce module, ouvrez RStudio dans votre SciViews Box, puis exécutez l’instruction suivante dans la fenêtre console :

BioDataScience::run("10b_anova_kruskal")

Appliquez l’analyse de variances ou le test de Kruskal-Wallis dans vos projets portant sur la biométrie humaine et sur le zooplankton.