7.1 Probabilités

La vidéo suivante vous introduit la notion de probabilité et le calcul de probabilités d’une manière plaisante à partir d’un jeu de hasard proposé par un petit chat à ses amis…

Sachant qu’un événement en statistique est un fait qui se produit, la probabilité que cet événement se produise effectivement peut être quantifiée sur base de l’observation des réalisations passées. Ainsi si l’événement en question s’est produit, disons, 9 fois sur un total de 12 réalisations, on dira que la probabilité que cet événement se produise est de 9/12, soit 0,75. Notez qu’une probabilité est un nombre compris entre zéro (lorsqu’il ne se produit jamais) et un (lorsqu’il se produit toujours).

On écrira, pour la probabilité de l’événement E :

\[0 \leq \mathrm{P}(E) \leq 1\]

7.1.1 Dépistage

Voyons tout de suite une application plus proche de la biologie : le dépistage d’une maladie qui touche 8% de la population. Le test de dépistage mis en place détecte 95% des malades. De plus, le test se trompe dans 10% des cas pour les personnes saines. Comment connaitre le risque d’être malade si on est diagnostiqué positif par ce test ?

Pour résoudre ce problème, nous devons d’abord apprendre à combiner des probabilités. Ce n’est pas bien compliqué. Si on a affaire à des événements successifs indépendants (c’est-à-dire que l’occurrence de l’un ne dépend pas de l’occurrence de l’autre), la probabilité que les deux événements successifs indépendants se produisent tous les deux est la multiplication des deux probabiltés. On pourra écrire :

\[\mathrm{P}(E_1 \,\mathrm{et}\, E_2) = \mathrm{P}(E_1) * \mathrm{P}(E_2)\]

Vous pouvez dès lors calculer la probabilité que l’on teste un patient malade (probabilité = 0,08) et que le test soit positif (0,95) dans ce cas :

# Personne malade et détectée positive
(p_sick_positive <- 0.08 * 0.95)

# [1] 0.076

Ceci n’indique pas la probabilité que le test soit positif car il est également parfois (erronément) positif pour des patients sains. Mais au fait, quelle est la probabilité d’avoir un patient sain ? La probabilité que l’un parmi tous les événements possibles se produise vaut toujours un. Les seuls événements possibles ici sont que le patient soit sain ou malade. Donc,

\[\mathrm{P}(sain) + \mathrm{P}(malade) = 1 \rightarrow \mathrm{P}(sain) = 1 - \mathrm{P}(malade) = 0.92\]

Nous pouvons maintenant déterminer la probabilité que le test soit positif dans le cas d’une personne saine :

# Personne saine et détectée positive
(p_healthy_positive <- 0.92 * 0.10)

# [1] 0.092

Bon, il nous reste à combiner les probabilités que le test soit positif si la personne est malade et si la personne est saine. Mais comment faire ? Ici, on n’a pas affaire à des événements successifs, mais à des évènements mutuellement exclusifs. On les appellent des événements disjoints. Pour déterminer si l’un parmi deux événements disjoints se produit, il suffit d’additionner leurs probabilités respectives. Nous pouvons maintenant déterminer la probabilité que le test soit positif quelle que soit la personne testée :

# La probabilité que le test soit positif 
(p_positive <- p_sick_positive + p_healthy_positive)

# [1] 0.168

Nous nous trouvons ici face à un résultat pour le moins surprenant ! En effet, nous constatons que le test est positif dans 16,8% des cas, mais seulement 7,6% du temps, il sera correct (probabilité d’une personne malade détectée). Parmi tous les cas positifs au test, il y en a…

p_sick_positive / p_positive

# [1] 0.452381

… seulement 45,2% qui sont effectivement malades (on parle de vrais positifs) ! Ceci ne correspond pas du tout aux indications de départ sur les performances du test.

Dans le cas de deux faits successifs qui ne peuvent chacun que résulter en deux événements, nous avons seulement quatre situations possibles. Si l’un des cas est qualifié de positif et l’autre de négatif, nous aurons :

les vrais positifs (test positif alors que la personne est malade), ici 0.08 * 0.95
les faux positifs (test positif alors que la personne est saine), ici 0.92 * 0.10
les vrais négatifs (test négatif alors que la personne est saine), ici 0.92 * 0.90
les faux négatifs (test négatif alors que la personne est malade), ici 0.08 * 0.05

En fait, les performances finales du test de dépistage dépendent aussi de la prévalence de la maladie. Ainsi pour une maladie très commune qui affecterait 80% de la population, nous obtenons :

# Faux positifs
0.20 * 0.10

# [1] 0.02

# Vrais positifs
0.80 * 0.95

# [1] 0.76

# Total des positifs
0.20 * 0.10 + 0.80 * 0.95

# [1] 0.78

# Fractions de tests positifs qui sont corrects
(0.80 * 0.95) / (0.20 * 0.10 + 0.80 * 0.95)

# [1] 0.974359

Ouf ! Dans ce cas-ci le test positif est correct dans 97,4% des cas. Mais qu’en serait-il si la maladie est très rare (probabilité de 0,008) ?

# Faux positifs
0.992 * 0.10

# [1] 0.0992

# Vrais positifs
0.008 * 0.95

# [1] 0.0076

# Total des positifs
0.992 * 0.10 + 0.008 * 0.95

# [1] 0.1068

# Fractions de tests positifs qui sont corrects
(0.008 * 0.95) / (0.992 * 0.10 + 0.008 * 0.95)

# [1] 0.07116105

Dans ce cas, un test positif n’aura effectivement détecté un malade que dans … 7,1% des cas ! Les 92,9% autres cas positifs seront en fait des personnes saines.

Comme nous pouvons le constater ici, le calcul des probabilités est relativement simple. Mais en même temps, les résultats obtenus peuvent être complètement contre-intuitifs. D’où l’intérêt de faire ce genre de calcul justement.

7.1.2 Arbre des probabilités

Il se peut que tout cela vous paraisse très (trop) abstrait. Vous êtes peut-être quelqu’un de visuel qui comprend mieux les concepts en image. Dans ce cas, la méthode alternative de résolution des calculs de probabilités via les arbres de probabilités devrait vous éclairer. Le principe consiste à représenter un arbre constitué de nœuds (des faits qui se produisent). De ces nœuds, vous représentez autant de branches (des segments de droites) que d’événements possibles. La figure suivante est l’arbre des probabilités correspondant au cas du dépistage de la maladie qui touche 8% de la population.

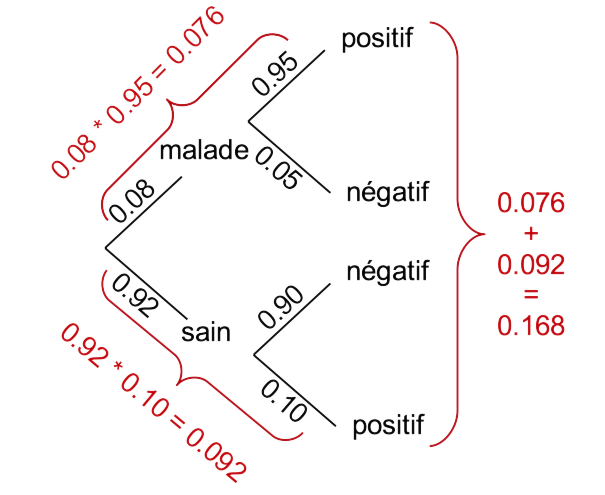
Arbre de probabilités permettant de déterminer la probabilité d’avoir un résultat positif au test.

Du premier nœud (le fait qu’une personne est atteinte ou non de la maladie), nous avons deux branches menant aux deux événements “malade” et “sain”. Chacune de ces deux situations est un nouveau nœud d’où deux événements sont possibles à chaque fois (2 fois 2 nouvelles branches) : un test “positif”, ou un test “négatif”. Les nœuds terminaux (les “négatifs” et “positifs” ici) sont aussi appelés les feuilles de l’arbre. L’arbre reprend donc tous les cas possibles depuis le nœud de départ (sa racine), jusqu’aux feuilles.

L’étape suivante consiste à aller indiquer le long des branches les probabilités associées à chaque événement : 0.08 pour “malade”, 0.95 pour un dépistage “positif” si la personne est malade, etc. A ce stade, une petite vérification peut être faite. La somme des probabilités aux feuilles doit toujours valoir un, et il en est de même de la somme de toutes les branches issues d’un même nœud.

Le calcul se fait ensuite comme suit. On repère tous les cas qui nous intéressent. Ici, il s’agit de toutes les trajectoires qui mènent à un test “positif”. Le calcul des probabilités se fait en multipliant les probabilités lorsqu’on passe d’un noeud à l’autre et en additionnant les probabilités ainsi calculées le long des feuilles terminales de l’arbre considéré. Donc, le chemin “malade” -> “positif” correspond à 0.08 * 0.95 = 0.076. Le chemin “sain” -> “positif” correspond à 0.92 * 0.10 = 0.092. Enfin, nous sommons les probabilités ainsi calculées pour toutes les feuilles de l’arbre qui nous intéressent. Ici, ce sont toutes les feuilles qui correspondent à un test “positif”, soit 0.076 + 0.092 = 0.168. Et voilà ! Nous avons répondu au problème : la probabilité d’avoir un résultat positif avec le test de dépistage dans un population dont 8% est atteint de la maladie est de 16.8%.

7.1.3 Théorème de Bayes

Nous devons introduire ici le concept de probabilité conditionnelle.

Une probabilité conditionnelle est la probabilité qu’un événement E2 se produise si et seulement si un premier événement E1 s’est produit (E1 et E2 sont deux événements successifs). La probabilité conditionnelle s’écrit \(\mathrm{P}(E2|E1)\).

Vous noterez que l’arbre des probabilités représente, en réalité, des probabilités conditionnelles à partir du second niveau (l’arbre peut être évidemment plus complexe).

Arbre de probabilités avec probabilités conditionnelles en rouge.

On pourra considérer, donc, la probabilité conditionnelle d’avoir un résultat positif au test, si la personne est malade \(\mathrm{P}(positif|malade)\). Vous l’avez indiquée plus haut dans l’arbre des probabilités, c’est 0.95. Maintenant, la probabilité qu’une personne soit malade si elle est positive au test \(\mathrm{P}(malade|positif)\) est une information capitale ici. Le lien entre les deux n’est pas facile à faire. C’est grâce aux travaux du révérend Thomas Bayes au 18^ème siècle que ce problème a été résolu. Les implications du théorème de Bayes sont énormes car cela permet de déterminer des probabilités dites a posteriori en fonction de connaissances a priori.

Si nous réanalysons le raisonnement qui est fait dans l’arbre de probabilités, on peut remarquer que le premier calcul (“malade” -> “positif”) correspond en fait à la probabilité que le test soit positif si le patient est malade \(\mathrm{P}(positif|malade)\) multipliée par la probabilité que le patient soit malade \(\mathrm{P}(malade)\), et ceci est aussi égal à \(\mathrm{P}(positif\, et\, malade)\). Donc,

\[\mathrm{P}(positif|malade) * \mathrm{P}(malade) = \mathrm{P}(positif\, et\, malade)\]

Par un raisonnement symétrique, on peut aussi dire que :

\[\mathrm{P}(malade|positif) * \mathrm{P}(positif) = \mathrm{P}(positif\, et\, malade)\]

Donc, nous avons aussi :

\[\mathrm{P}(malade|positif) * \mathrm{P}(positif) = \mathrm{P}(positif|malade) * \mathrm{P}(malade)\] … et en divisant les deux termes par \(\mathrm{P}(positif)\), on obtient :

\[\mathrm{P}(malade|positif) = \frac{\mathrm{P}(positif|malade) * \mathrm{P}(malade)}{\mathrm{P}(positif)}\]

De manière générale, le théorème de Bayes s’écrit :

\[\mathrm{P}(A|B) = \frac{\mathrm{P}(B|A) * \mathrm{P}(A)}{\mathrm{P}(B)}\]

Nous avons maintenant une façon simple de déterminer \(\mathrm{P}(malade|positif)\) à partir de \(\mathrm{P}(positif|malade)\), \(\mathrm{P}(malade)\), et \(\mathrm{P}(positif)\), c’est-à-dire des probabilités auxquelles nous avons facilement accès expérimentalement en pratique. Calculez comme exercice la probabilité qu’un patient soit malade s’il est positif au test via le théorème de Bayes, et comparez le résultat de votre calcul à ce que nous avions obtenu plus haut (45.2%).

A retenir

Probabilité d’un événement :

\[\mathrm{P}(E) = \frac{\mathrm{nbr\ occurences\ } E}{\mathrm{nbr\ total\ essais}}\]

Probabilité de deux événements successifs (cas général) :

\[\mathrm{P(A\, \mathrm{et}\, B)} = \mathrm{P}(B|A) * \mathrm{P(A)}\]

Probabilité qu’un parmi deux événements se produise (cas général) :

\[\mathrm{P(A\, \mathrm{ou}\, B)} = \mathrm{P}(A) + \mathrm{P(B)} - \mathrm{P}(A\, \mathrm{et}\, B)\]

Application vraiment utile du théorème de Bayes par xkcd.

Pour en savoir plus

Une autre explication du théorème de Bayes (en anglais).

7.1.4 Probabilités et contingence

Comme un tableau de contingence indique le nombre de fois que des événements ont pu être observés, il peut servir de base à des calculs de probabilités. Partons du dénombrement de fumeur en fonction du revenu dans une population.

tabac <- data.frame(
  revenu_faible = c(634,1846,2480),
  revenu_moyen = c(332, 1622,1954),
  revenu_eleve = c(247,1868,2115),
  total = c(1213, 5336, 6549))
rownames(tabac) <- c("fume", "ne fume pas",  "total")
knitr::kable(tabac)

	revenu_faible	revenu_moyen	revenu_eleve	total
fume	634	332	247	1213
ne fume pas	1846	1622	1868	5336
total	2480	1954	2115	6549

Quelle est la probabilité d’être un fumeur \(\mathrm{P}(fumeur)\) ? Rappelons-nous de la définition de probabilité : nombre de cas où l’événement se produit sur le nombre total de cas. Ici, on a 1213 fumeurs dans un effectif total de l’échantillon de 6549 personnes, soit :

1213 / 6549

# [1] 0.1852191

Quelle est la probabilité d’être fumeur si le revenu élevé \(\mathrm{P}(fumeur|revenu\_eleve)\) ? Le nombre de fumeurs à revenus élevés se monte à 247. Attention, ici l’échantillon de référence n’est plus la population totale, mais seulement ceux qui ont des revenus élevés, donc 2115 personnes :

247 / 2115

# [1] 0.1167849

Quelle est la probabilités d’avoir un revenu faible ou d’avoir un élevé ? Cette question peut s’écrire : \(\mathrm{P}(revenu\-faible\, ou\, revenu\_eleve)\).

2480 / 6549 + 2115 / 6549

# [1] 0.7016338

Il s’agit d’une somme de probabilités disjointes.

Quelle est la probabilités d’être fumeur ou d’avoir un revenu moyen ? Cette question peut s’écrire : \(\mathrm{P}(fumeur\, ou\, revenu\_moyen)\).

1213 / 6549 + 1954 / 6549 - 332 / 6549

# [1] 0.4328905

Il s’agit d’une somme de probabilités non disjointes³⁰.

7.1.4.1 Populations de taille infinie

Dans une population, voici les proportions de différents groupes sanguins :

44% O, 42% A, 10% B, 4% AB

Quelles est la probabilité d’obtenir 1 individu du groupe B ? Cette question peut s’écrire : \(\mathrm{P}(B)\).

0.10

# [1] 0.1

Quelle est la probabilité d’obtenir 3 individus du groupe B d’affilée ? Cette question peut s’écrire : \(\mathrm{P}(B\, et\, B\, et\, B)\).

0.10 * 0.10 * 0.10

# [1] 0.001

Nous avons ici 3 événements successifs indépendants. Donc, on multiplie leurs probabilités respectives.

7.1.4.2 Populations de taille finie

Dans une population de 100 personnes dont les proportions des différentes groupes sanguins sont identiques au cas précédent.

Quelles est la probabilité d’obtenir un échantillon de trois individus du groupe B issus de cette population³¹ ? Cette question peut s’écrire : \(\mathrm{P}(B\, et\, B\, et\, B)\).

10 / 100 * 9 / 99 * 8 / 98

# [1] 0.000742115

Il s’agit d’événements successifs non-indépendants. En effet, le retrait d’un individu de la population de taille finie modifie les proportions relatives des groupes sanguins dans le reste de la population, et donc, les probabilités aux tirages suivants. Ainsi pour le groupe B, nous n’avons plus que 9 individus de ce groupe dans une population de 99 individus après le premier tirage d’un individu du groupe B ! Autrement dit, \(\mathrm{P}(B|B) \neq \mathrm{P}(B|not\ B)\). On a donc, \(\mathrm{P}(B|B) = 9/99\) et ensuite \(\mathrm{P}(B|B\, \mathrm{et}\, B) = 8/98\).

A vous de jouer

Ouvrez RStudio dans votre SciViews Box, puis exécutez l’instruction suivante dans la fenêtre console :

BioDataScience::run("07a_proba")

Si E1 et E2 sont deux événements non disjoints, la probabilité que l’un de ces deux événements se produise est : \(\mathrm{P}(E1\, ou\, E2) = \mathrm{P}(E1) + \mathrm{P}(E2) - \mathrm{P}(E1\, et\, E2)\).↩
En statistique, on appelle cela un tirage au sort sans remise. Le résultat est très différent si le premier individu tiré au hasard était remis dans la population et pouvait être éventuellement pris à nouveau au second ou troisième tirage (tirage au sort avec remise). Notez aussi que, pour une population de taille infinie ou quasi-infinie, les deux types de tirage au sort sont équivalents à celui avec remise car enlever un individu d’une population infinie ne change pas fondamentalement son effectif, donc les probabilités ultérieures.↩