4.1 Graphique en barres
Le graphique en barres (on dit aussi graphique en bâtons) compare les effectifs pour différents niveaux (ou modalités) d’une variable qualitative ou facteur. La différence avec l’histogramme est donc subtile et tient au fait que, pour l’histogramme, nous partons d’une variable quantitative qui est découpée en classes.
4.1.1 Effectifs par facteur
La question du nombre et/ou de l’intervalle des classes ne se pose pas dans le cas du graphique en barres. Par défaut, les barres seront séparées les unes des autres par un petit espace vide pour bien indiquer visuellement qu’il n’y a pas continuité entre les classes (dans l’histogramme, les barres sont accolées les unes aux autres pour matérialiser justement cette continuité).
La formule que vous utiliserez, ici encore, ne fait appel qu’à une seule variable et s’écrira donc :
\[\sim variable \ facteur\]
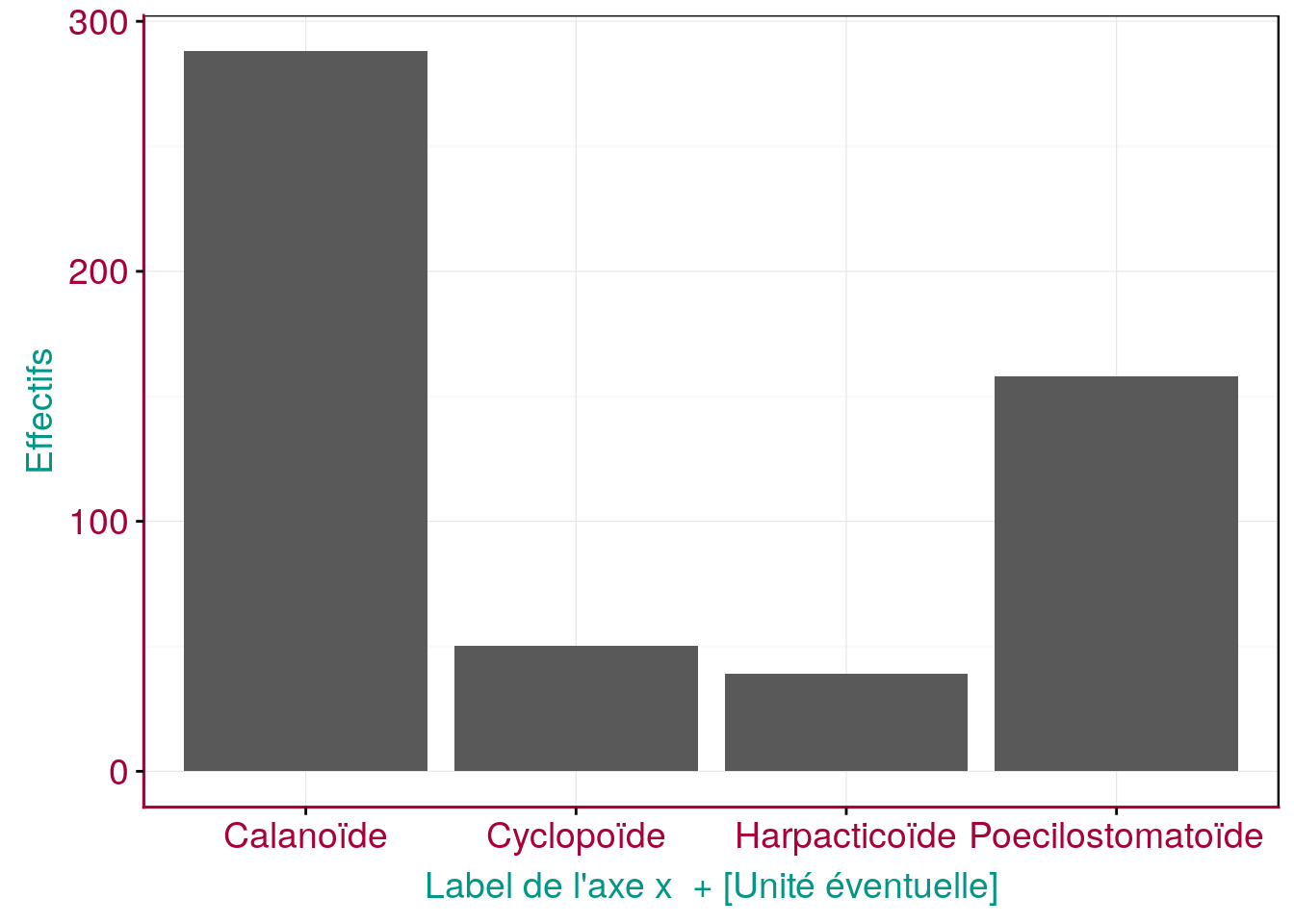
Figure 4.1: Exemple d’un graphique en barres montrant le dénombrement des niveaux d’une variable facteur, avec les éléments importants du graphique mis en évidence en couleurs.
Outre les barres elles-mêmes, prêtez toujours attention aux éléments suivants du graphique (ici mis en évidence en couleurs) :
- les axes avec les graduations (en rouge)
- les niveaux de la variable facteur (en rouge également)
- le label des axes (en bleu)
Les instructions dans R pour produire un graphique en barres à l’aide de la fonction chart() sont :
# Importation du jeu de données
(zooplankton <- read("zooplankton", package = "data.io", lang = "FR"))# # A tibble: 1,262 x 20
# ecd area perimeter feret major minor mean mode min max std_dev
# <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 0.770 0.465 4.45 1.32 1.16 0.509 0.363 0.036 0.004 0.908 0.231
# 2 0.700 0.385 2.32 0.728 0.713 0.688 0.361 0.492 0.024 0.676 0.183
# 3 0.815 0.521 4.15 1.33 1.11 0.598 0.308 0.032 0.008 0.696 0.204
# 4 0.785 0.484 4.44 1.78 1.56 0.394 0.332 0.036 0.004 0.728 0.218
# 5 0.361 0.103 1.71 0.739 0.694 0.188 0.153 0.016 0.008 0.452 0.110
# 6 0.832 0.544 5.27 1.66 1.36 0.511 0.371 0.02 0.004 0.844 0.268
# 7 1.23 1.20 15.7 3.92 1.37 1.11 0.217 0.012 0.004 0.784 0.214
# 8 0.620 0.302 3.98 1.19 1.04 0.370 0.316 0.012 0.004 0.756 0.246
# 9 1.19 1.12 15.3 3.85 1.34 1.06 0.176 0.012 0.004 0.728 0.172
# 10 1.04 0.856 7.60 1.89 1.66 0.656 0.404 0.044 0.004 0.88 0.264
# # … with 1,252 more rows, and 9 more variables: range <dbl>, size <dbl>,
# # aspect <dbl>, elongation <dbl>, compactness <dbl>, transparency <dbl>,
# # circularity <dbl>, density <dbl>, class <fct># Réduction du jeu de données
(copepoda <- filter(zooplankton,
class %in% c("Calanoïde", "Cyclopoïde", "Harpacticoïde", "Poecilostomatoïde")))# # A tibble: 535 x 20
# ecd area perimeter feret major minor mean mode min max std_dev
# <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 0.770 0.465 4.45 1.32 1.16 0.509 0.363 0.036 0.004 0.908 0.231
# 2 0.815 0.521 4.15 1.33 1.11 0.598 0.308 0.032 0.008 0.696 0.204
# 3 0.785 0.484 4.44 1.78 1.56 0.394 0.332 0.036 0.004 0.728 0.218
# 4 0.361 0.103 1.71 0.739 0.694 0.188 0.153 0.016 0.008 0.452 0.110
# 5 0.832 0.544 5.27 1.66 1.36 0.511 0.371 0.02 0.004 0.844 0.268
# 6 1.23 1.20 15.7 3.92 1.37 1.11 0.217 0.012 0.004 0.784 0.214
# 7 0.620 0.302 3.98 1.19 1.04 0.370 0.316 0.012 0.004 0.756 0.246
# 8 1.19 1.12 15.3 3.85 1.34 1.06 0.176 0.012 0.004 0.728 0.172
# 9 1.04 0.856 7.60 1.89 1.66 0.656 0.404 0.044 0.004 0.88 0.264
# 10 0.725 0.412 7.14 1.90 0.802 0.655 0.209 0.008 0.004 0.732 0.202
# # … with 525 more rows, and 9 more variables: range <dbl>, size <dbl>,
# # aspect <dbl>, elongation <dbl>, compactness <dbl>, transparency <dbl>,
# # circularity <dbl>, density <dbl>, class <fct># Réalisation du graphique
chart(data = copepoda, ~ class) +
geom_bar() +
ylab("Effectifs")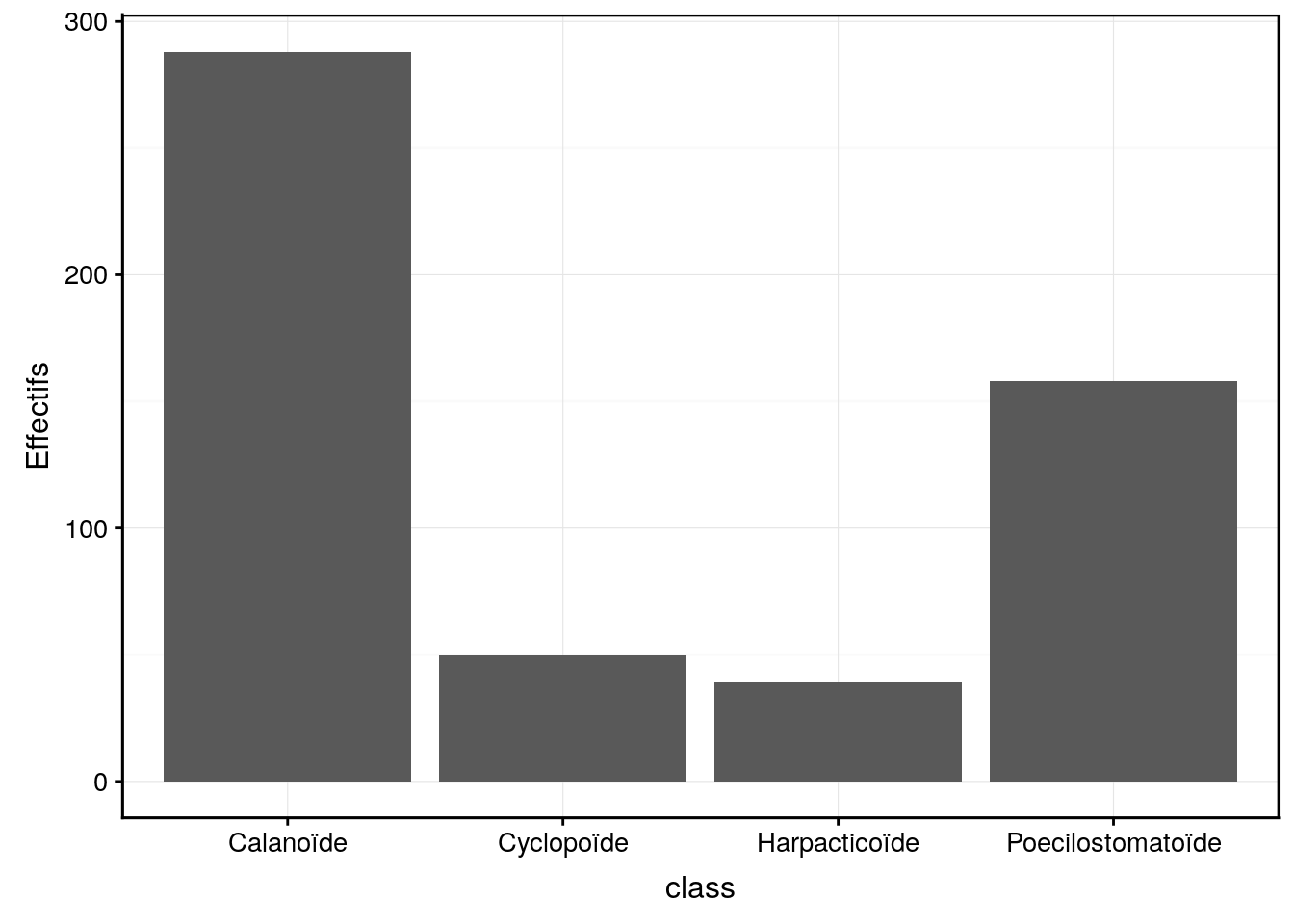
Figure 4.2: Abondances de quatres types de copépodes dans un échantillon de zooplancton.
La fonction geom_bar() se charge d’ajouter les barres verticales dans le graphique. La hauteur de ces barres correspond au nombre d’observations rencontrées dans le jeu de données pour chaque niveau (ou classe, ou groupe) de la variable facteur représentée.
4.1.2 Effectifs par 2 facteurs
# Importation des données biometry
(biometry <- read("biometry", package = "BioDataScience", lang = "FR"))# # A tibble: 395 x 7
# gender day_birth weight height wrist year_measure age
# <fct> <date> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 H 1995-03-11 69 182 15 2013 18
# 2 H 1998-04-03 74 190 16 2013 15
# 3 H 1967-04-04 83 185 17.5 2013 46
# 4 H 1994-02-10 60 175 15 2013 19
# 5 F 1990-12-02 48 167 14 2013 23
# 6 F 1994-07-15 52 179 14 2013 19
# 7 F 1971-03-03 72 167 15.5 2013 42
# 8 F 1997-06-24 74 180 16 2013 16
# 9 H 1972-10-26 110 189 19 2013 41
# 10 H 1945-03-15 82 160 18 2013 68
# # … with 385 more rows# Conversion de la variable year_measure de numérique à facteur
biometry$year_measure <- as.factor(biometry$year_measure)
label(biometry$year_measure) <- "Année de la mesure"Différentes représentations sont possibles pour observer des dénombrements tenant compte de plusieurs variables facteurs. Par défaut, l’argument position = a pour valeur par défaut stack (donc, lorsque cet argument n’est pas précisé dans geom_bar()).
a <- chart(data = biometry, ~ gender) +
geom_bar() +
ylab("Effectifs")
b <- chart(data = biometry, ~ gender %fill=% year_measure) +
geom_bar() +
ylab("Effectifs") +
scale_fill_viridis_d()
combine_charts(list(a, b), common.legend = TRUE)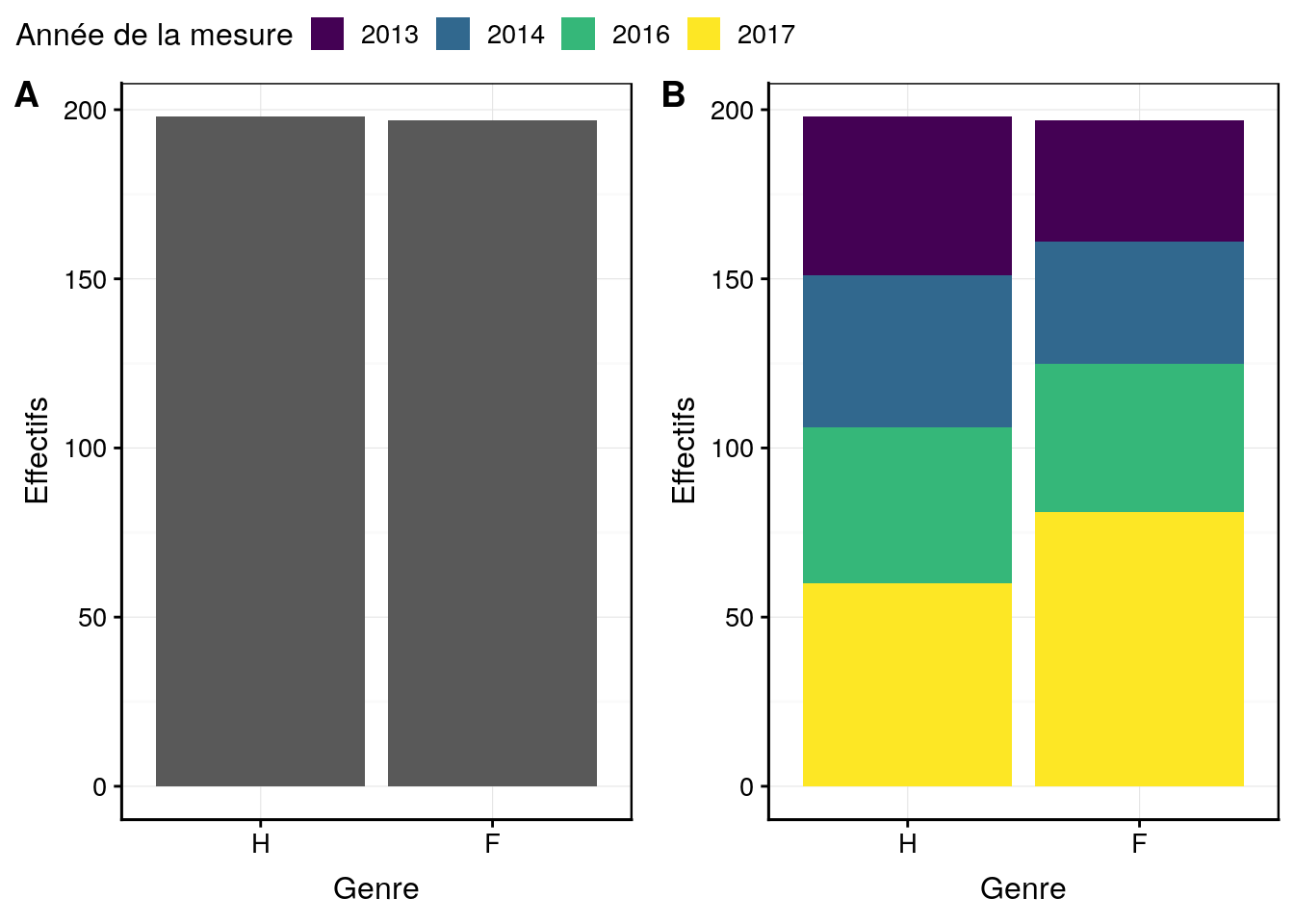
Figure 4.3: Dénombrement des hommes (H) et des femmes (F) dans l’étude sur l’obésité en Hainaut en tenant compte des années de mesure pour (B).
Il existe d’autres options en utilisant la valeur dodge ou fill pour l’argument position =.
a <- chart(data = biometry, ~ gender %fill=% year_measure) +
geom_bar(position = "stack") +
ylab("Effectifs") +
scale_fill_viridis_d()
b <- chart(data = biometry, ~ gender %fill=% year_measure) +
geom_bar(position = "dodge") +
ylab("Effectifs") +
scale_fill_viridis_d()
c <- chart(data = biometry, ~ gender %fill=% year_measure) +
geom_bar(position = "fill") +
ylab("Fractions") +
scale_fill_viridis_d()
combine_charts(list(a, b, c), common.legend = TRUE)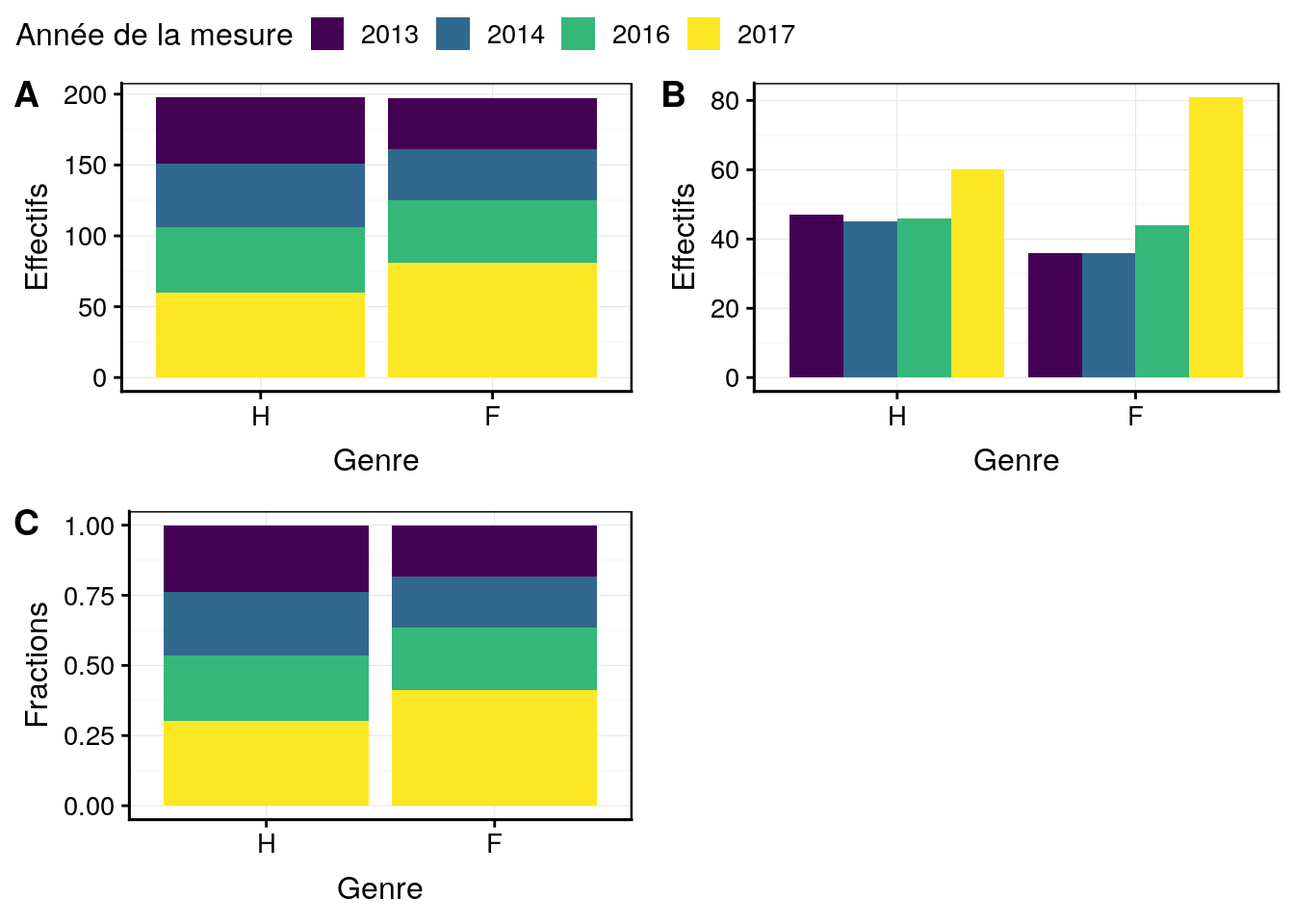
Figure 4.4: Dénombrement des hommes (H) et des femmes (F) dans l’étude sur l’obésité en Hainaut en tenant compte des années de mesure (différentes présentations).
Soyez vigilant à la différence entre l’argument position = stack et position = fill qui malgré un rendu semblable ont l’axe des ordonnées qui diffère (dans le cas de fill, il s’agit de la fraction par rapport au total qui est représentée, et non pas des effectifs absolus dénombrés).
Pièges et Astuces
Réordonner la variable facteur par fréquence
Vous pouvez avoir le souhait d’ordonner votre variable facteur afin d’améliorer le rendu visuel de votre graphique. Pour cela, vous pouvez employer la fonction fct_infreq().
chart(data = copepoda, ~ fct_infreq(class)) +
geom_bar() +
labs(x = "Classe", y = "Effectifs")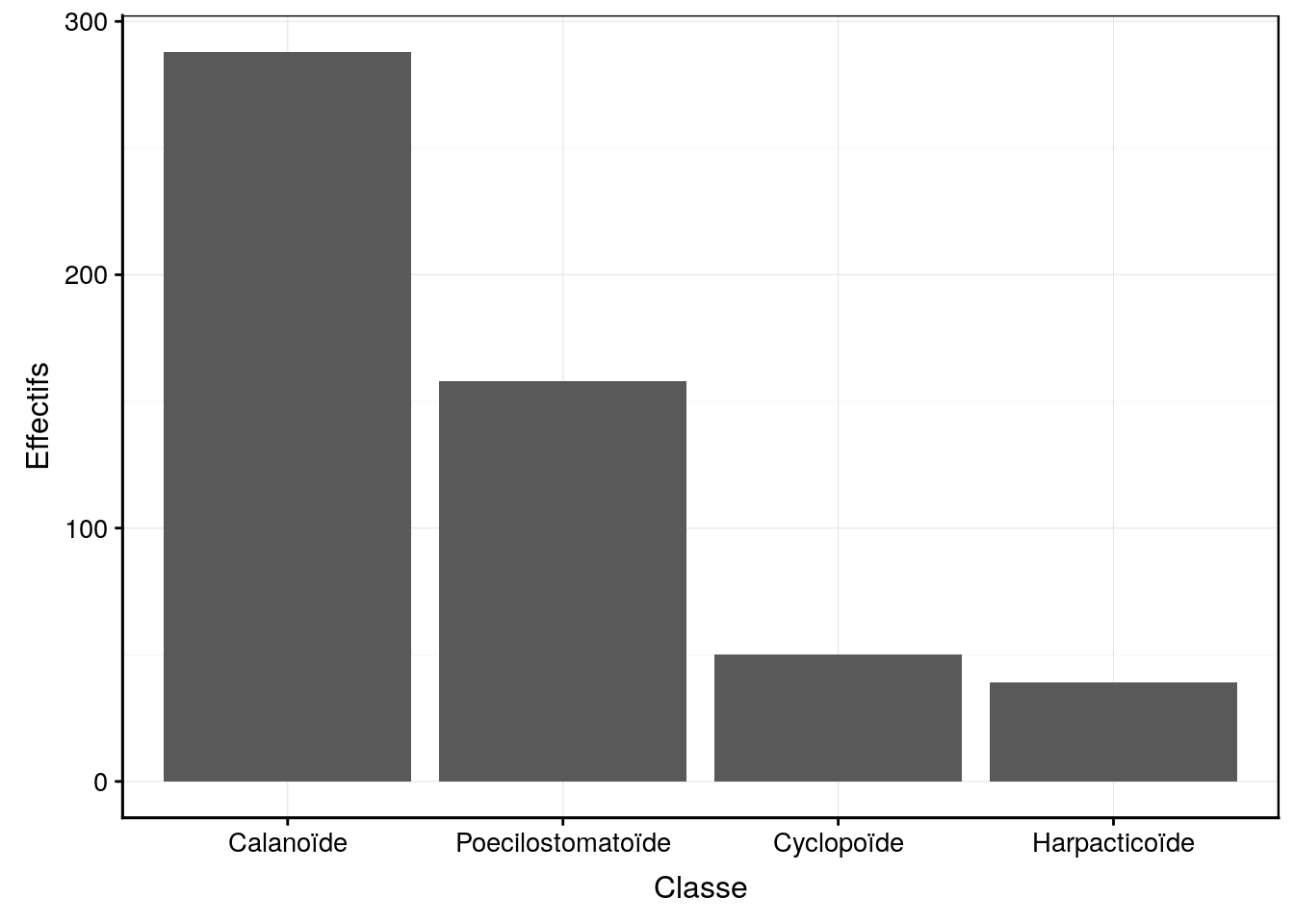
Figure 4.5: Dénombrement des classes de copépodes du jeu de données zooplankton.
Rotation des axes du graphique en barre
Lorsque les niveaux dans la variable étudiée sont trop nombreux, les légendes en abscisse risquent de se chevaucher, comme dans la Fig. 4.6
chart(data = zooplankton, ~ class) +
geom_bar() +
ylab("Effectifs")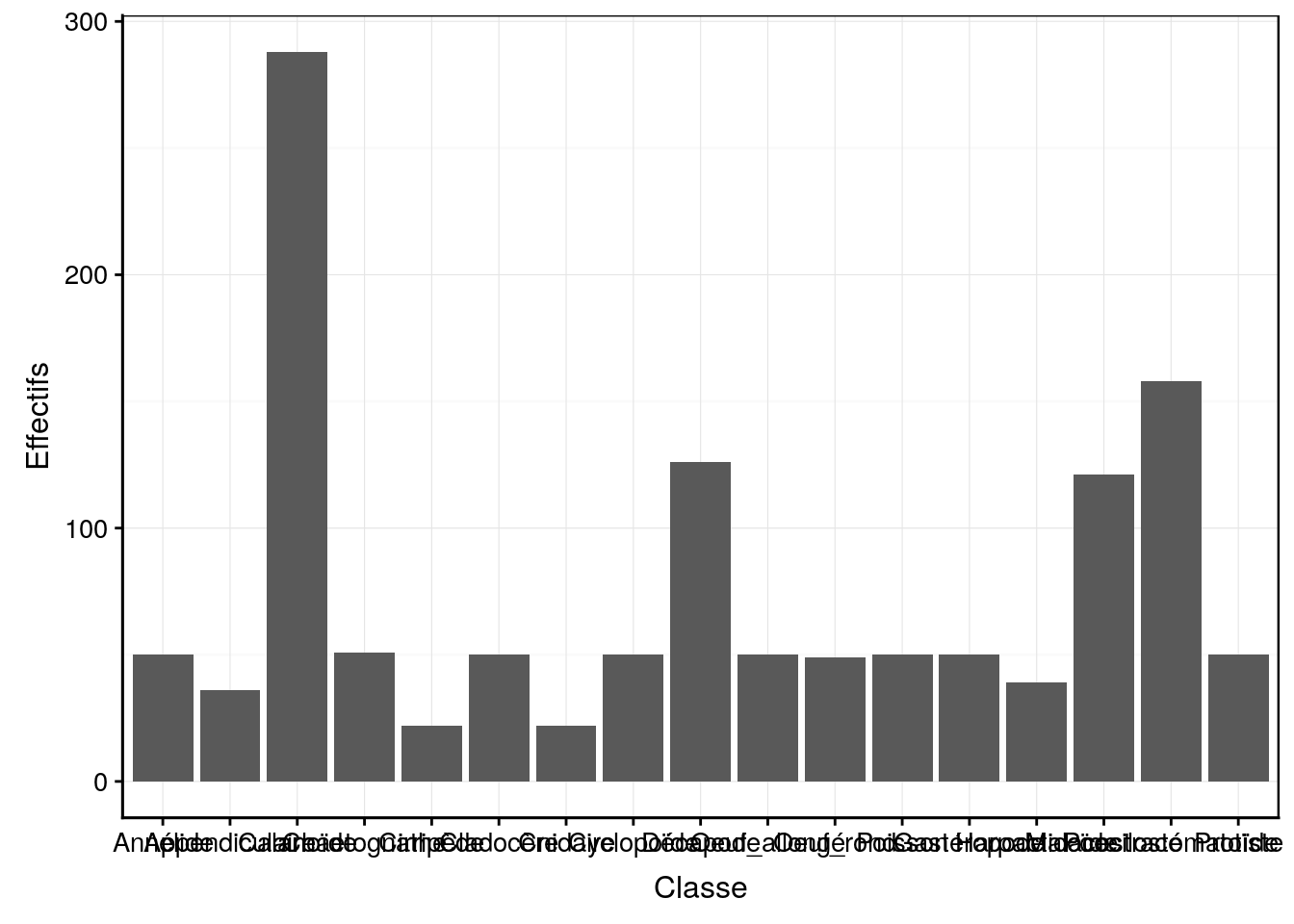
Figure 4.6: Dénombrement des classes du jeu de données zooplankton.
Avec la fonction coord_flip() ajoutée à votre graphique, vous pouvez effectuer une rotation des axes pour obtenir un graphique en barres horizontales. De plus, l’œil humain perçoit plus distinctement les différences de longueurs horizontales que verticales. Donc, de ce point de vue, le graphe en barres horizontal est considéré comme meilleur que le graphe en barres verticales.
chart(data = zooplankton, ~ class) +
geom_bar() +
ylab("Effectifs") +
coord_flip()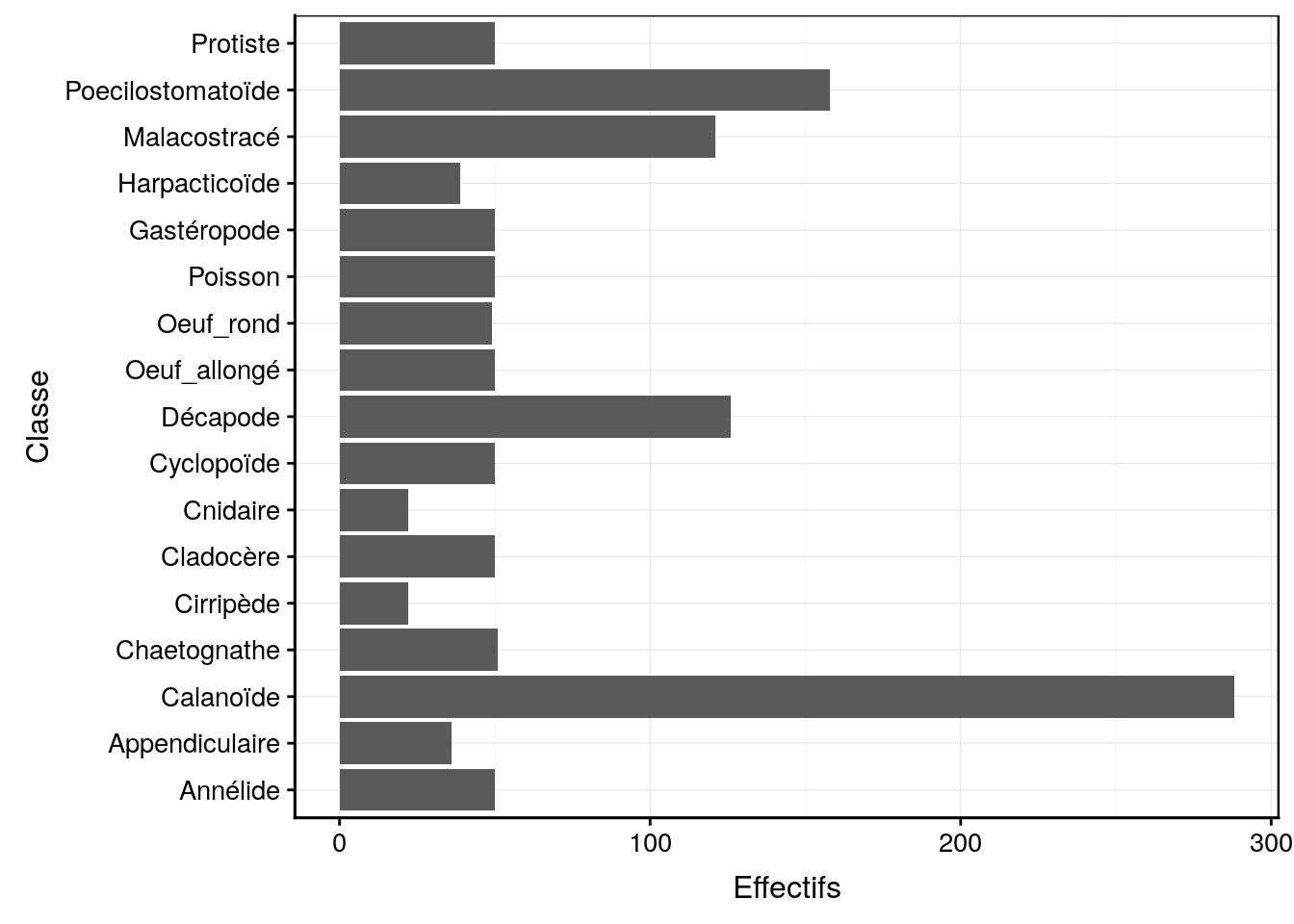
Figure 4.7: Dénombrement des classes du jeu de données zooplankton (version avec barres horizontales).
Pour en savoir plus
Graphes en barres à l’aide de ggplot2. Un tutoriel en français utilisant la fonction
ggplot(). L’annotation des barres est également présentée.Page d’aide de la fonction
geom_bar()en anglais.Autres exemples de graphes en barres à l’aide de `
ggplot().
4.1.3 Valeurs moyennes
Le graphique en barres peut être aussi employé pour résumer des données numériques via la moyenne. Il ne s’agit plus de dénombrer les effectifs d’une variable facteur mais de résumer des données numériques en fonction d’une variable facteur. On peut exprimer cette relation dans R sous la forme de
\[y \sim x\]
que l’on peut lire :
\[y \ en \ fonction \ de \ x\]
Avec y une variable numérique et x une variable facteur. Considérez l’échantillon suivant :
1, 71, 55, 68, 78, 60, 83, 120, 82 ,53, 26Calculez la moyenne sur base de la formule de la moyenne
\[\overline{y} = \sum_{i = 1}^n \frac{y_i}{n}\]
# Création du vecteur
x <- c(1, 71, 55, 68, 78, 60, 83, 120, 82, 53, 26)
# Calcul de la moyenne
mean(x)# [1] 63.36364Les instructions pour produire ce graphe en barres à l’aide de chart() sont :
chart(data = copepoda, size ~ class) +
stat_summary(geom = "col", fun.y = "mean")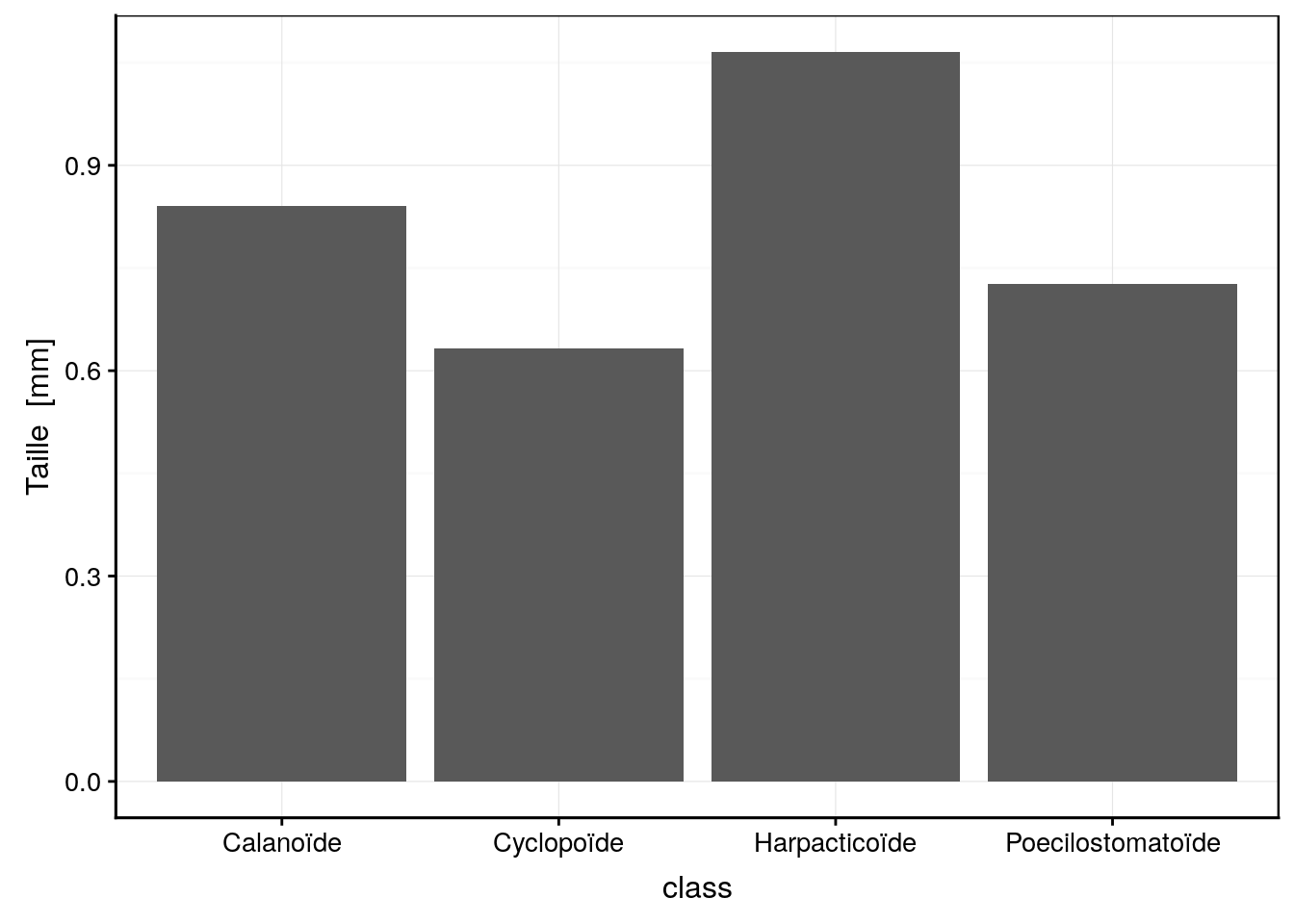
Figure 4.8: Exemple de graphique en barres représentant les moyennes de tailles par groupe zooplanctonique.
Ici, nous faisons appel à une autre famille de fonctions : celles qui effectuent des calculs sur les données avant de les représenter graphiquement.
Pour en savoir plus
Beware of dynamite. Démonstration de l’impact d’un graphe en barres pour représenter la moyenne (et l’écart type) = graphique en “dynamite”.
Dynamite plots : unmitigated evil? Une autre comparaison du graphe en dynamite avec des représentations alternatives qui montre que le premier peut avoir quand même quelques avantages dans des situations particulières.