4.3 Boite de dispersion

Vous souhaitez représenter graphiquement cette fois un résumé d’une variable numérique mesurée sur un nombre (relativement) important d’individus, soit depuis une dizaine jusqu’à plusieurs millions. Vous souhaitez également conserver de l’information sur la distribution des données, et voulez éventuellement comparer plusieurs distributions entre elles : soit différentes variables, soit différents niveaux d’une variable facteur. Nous avons déjà vu au module 3 les diagrammes en violon et en lignes de crêtes pour cet usage. Nous allons étudier ici les boites de dispersion (encore appelée boite à moustaches) comme option alternative intéressante. La boite de dispersion représentera graphiquement cinq descripteurs appelés les cinq nombres.

Considérez l’échantillon suivant :

1, 71, 55, 68, 78, 60, 83, 120, 82 ,53, 26

Ordonnez-le de la plus petite à la plus grande valeur :

# Créer du vecteur
x <- c(1, 71, 55, 68, 78, 60, 83, 120, 82, 53, 26)
# Ordonner le vecteur par ordre croissant
sort(x)

#  [1]   1  26  53  55  60  68  71  78  82  83 120

Le premier descripteur des cinq nombres est la médiane qui est la valeur se situant à la moitié des observations, donc, avec autant d’observations plus petites et d’observations plus grande qu’elle. La médiane sépare l’échantillon en deux.

median(x)

# [1] 68

Les quartiles séparent l’échantillon en quatre. Le premier quartile (Q1) sera la valeur pour laquelle 25% des observations seront plus petites. Elle se situe donc entre la valeur minimale et la médiane. Cette médiane est égale au second quartile (50% des observations plus petites). Le troisième quartile (Q3) est la valeur pour laquelle 75% des observations de l’échantillon sont plus petites¹³. Enfin, la valeur minimale et la valeur maximale observées dans l’échantillon complètent ces cinq nombres qui décrivent de manière synthétique la position et l’étendue des observations.

Les cinq nombres sont : la valeur minimale, le premier quartile, la médiane (ou deuxième quartile), le troisième quartile et la valeur maximale.

Voici comment on les calcules facilement dans R :

fivenum(x)

# [1]   1  54  68  80 120

La boite de dispersion est une représentation graphique codifiée de ces cinq nombres. La représentation de x sous forme de nuage de points n’est ni très esthétique, ni très lisible, surtout si nous avons affaire à des milliers ou des millions d’observations qui se chevauchent sur le graphique¹⁴.

Figure 4.12: Nuage de points univarié.

La boite de dispersion va remplacer cette représentation peu lisible par un objet géométrique qui représente les cinq nombres.

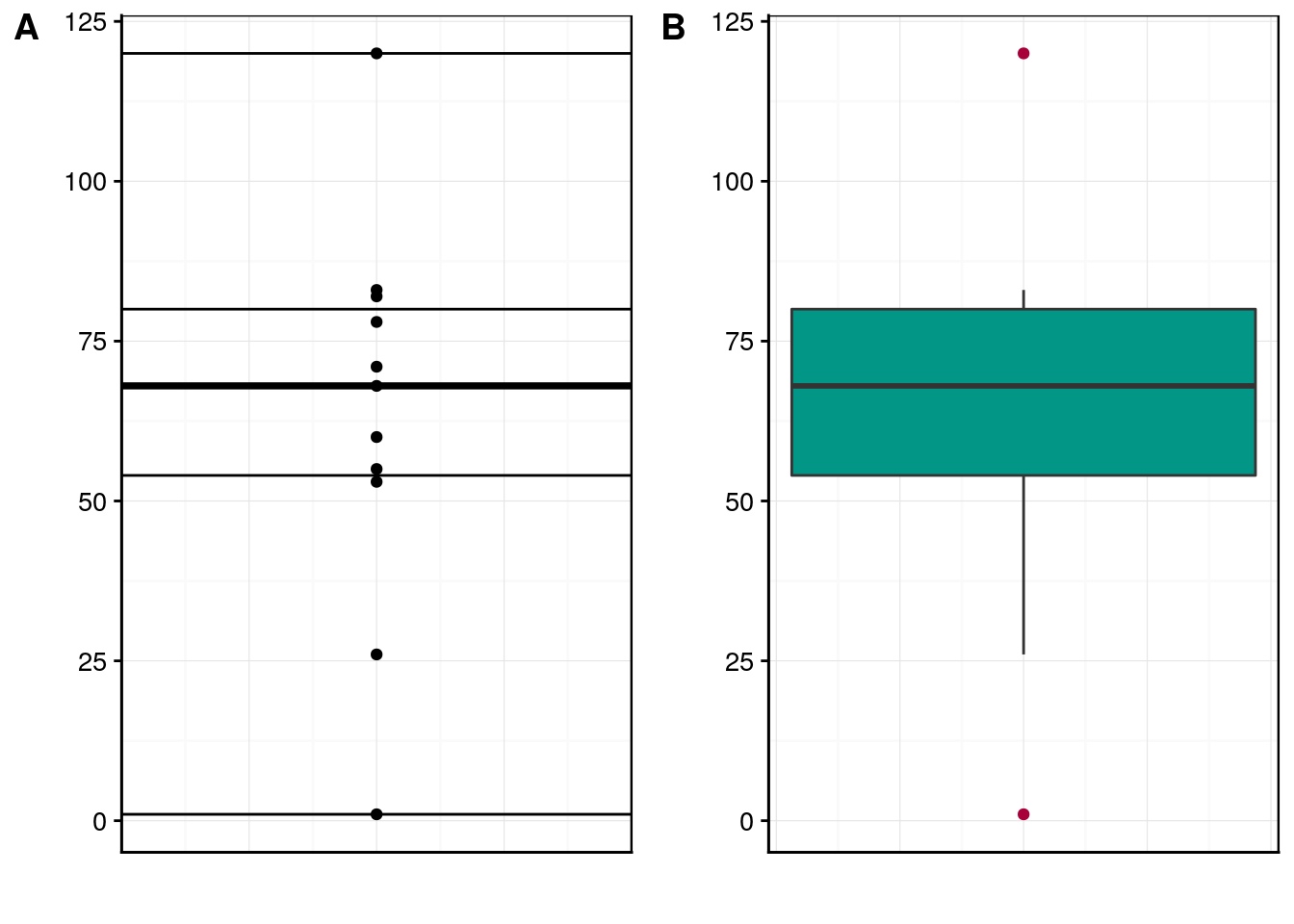
Figure 4.13: A) Nuage de points annoté avec les cinq nombres représentés par des traits horizontaux. B) Boite de dispersion obtenue pour les même données que A.

Vous observez à la Fig. 4.13 que certaines valeurs minimales et maximales ne sont pas reliées à la boite de dispersion, il s’agit de valeurs extrêmes.

Règle pour déterminer s’il y a des valeurs extrêmes avec une boite de dispersion : une valeur est considérée comme extrême si son écart par rapport à la boite est supérieur à une fois et demi la hauteur de la boite (encore appelée espace inter-quartile IQR correspondant à Q3 - Q1). Les tiges (ou “moustaches”) qui prolongent la boite de dispersion s’arrêtent donc aux dernières valeurs les plus petites et plus grandes, mais qui rentrent encore dans une fois et demi l’IQR. Les valeurs extrêmes sont ensuite représentées individuellement par un point au dessus et en dessous.

La boite de dispersion finale ainsi que sa description sont représentées à la Fig. 4.14 ci-dessous.

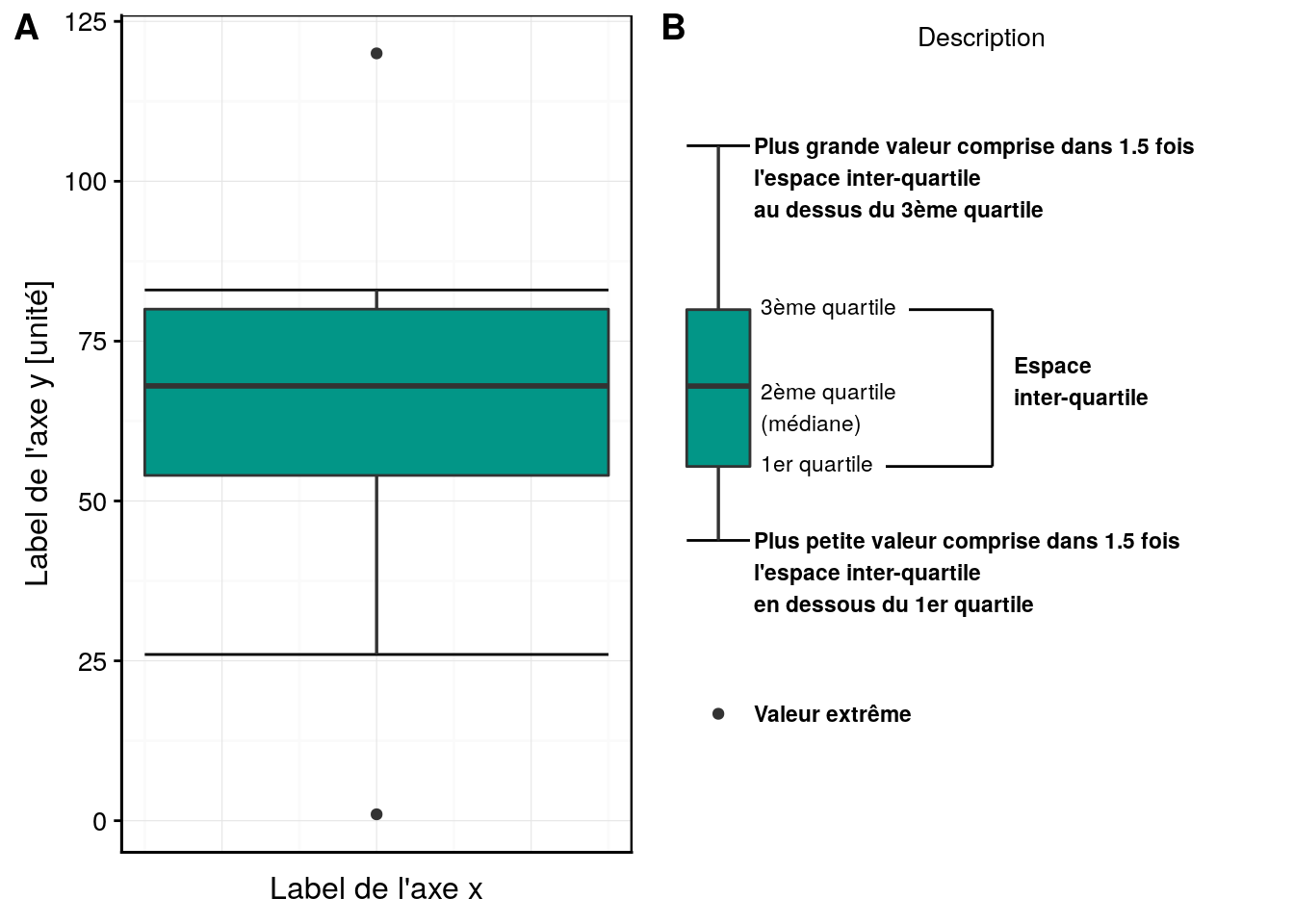
Figure 4.14: A) Boite de dispersion pour x et B) description des différents éléments constitutifs.

Les instructions dans R pour produire un graphique en boites de dispersion parallèles (comparaison de la distribution d’une variable numérique pour différents niveaux d’une autre variable facteur) sont :

chart(data = copepoda, size ~ class) +
  geom_boxplot()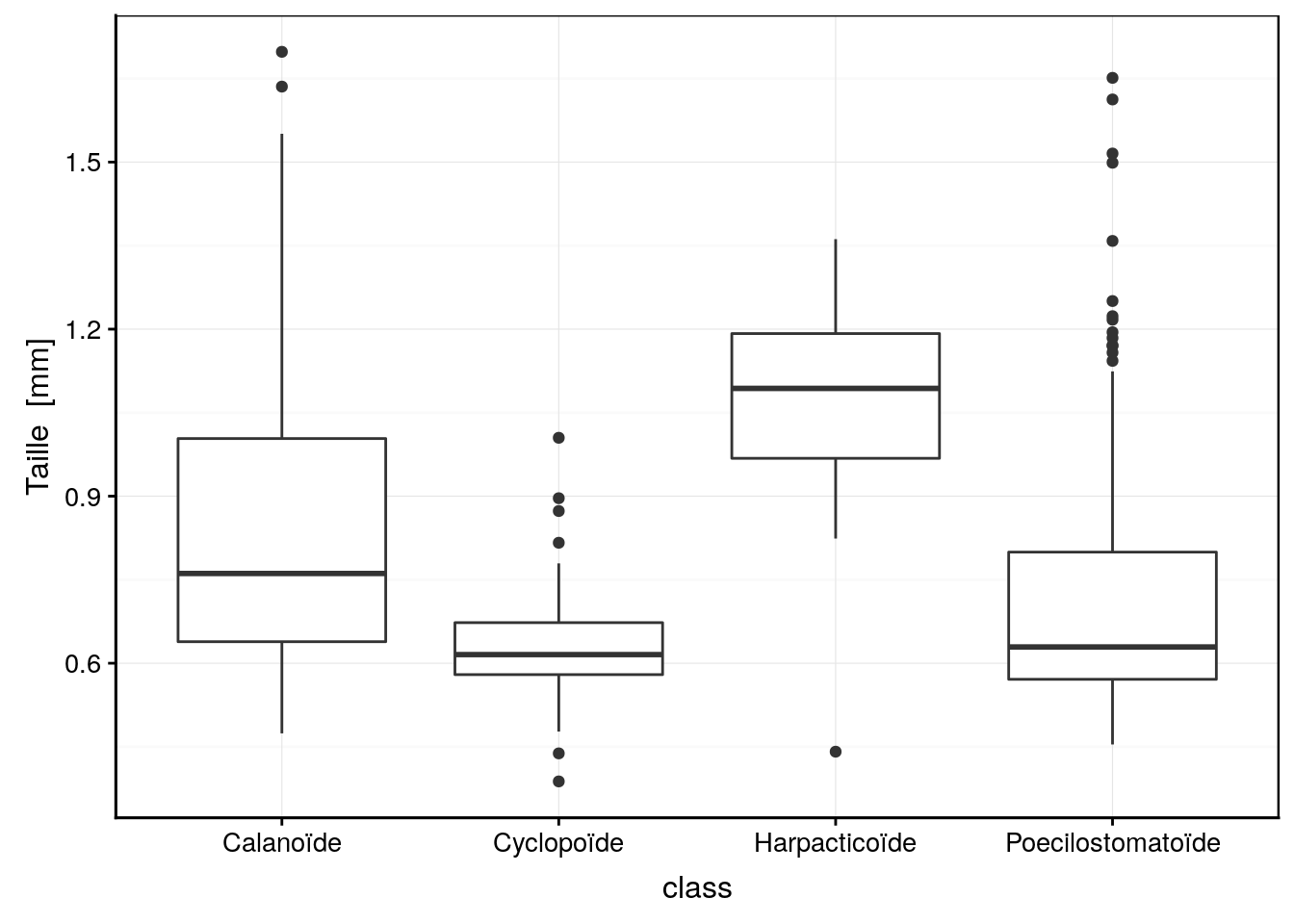

Figure 4.15: Distribution des tailles par groupes taxonomiques pour le zooplancton.

La formule à employer est YNUM (size) ~ XFACTOR (class). Ensuite, pour réaliser une boite de dispersion vous devez ajouter la fonction geom_boxplot().

4.3.1 Taille de l’échantillon

Lors de la réalisation de boites de dispersion, vous devez être vigilant au nombre d’observations qui se cachent sous chacune d’elles. En effet, réaliser une boite de dispersion à partir d’échantillons ne comportant que cinq valeurs ou moins n’a aucun sens !

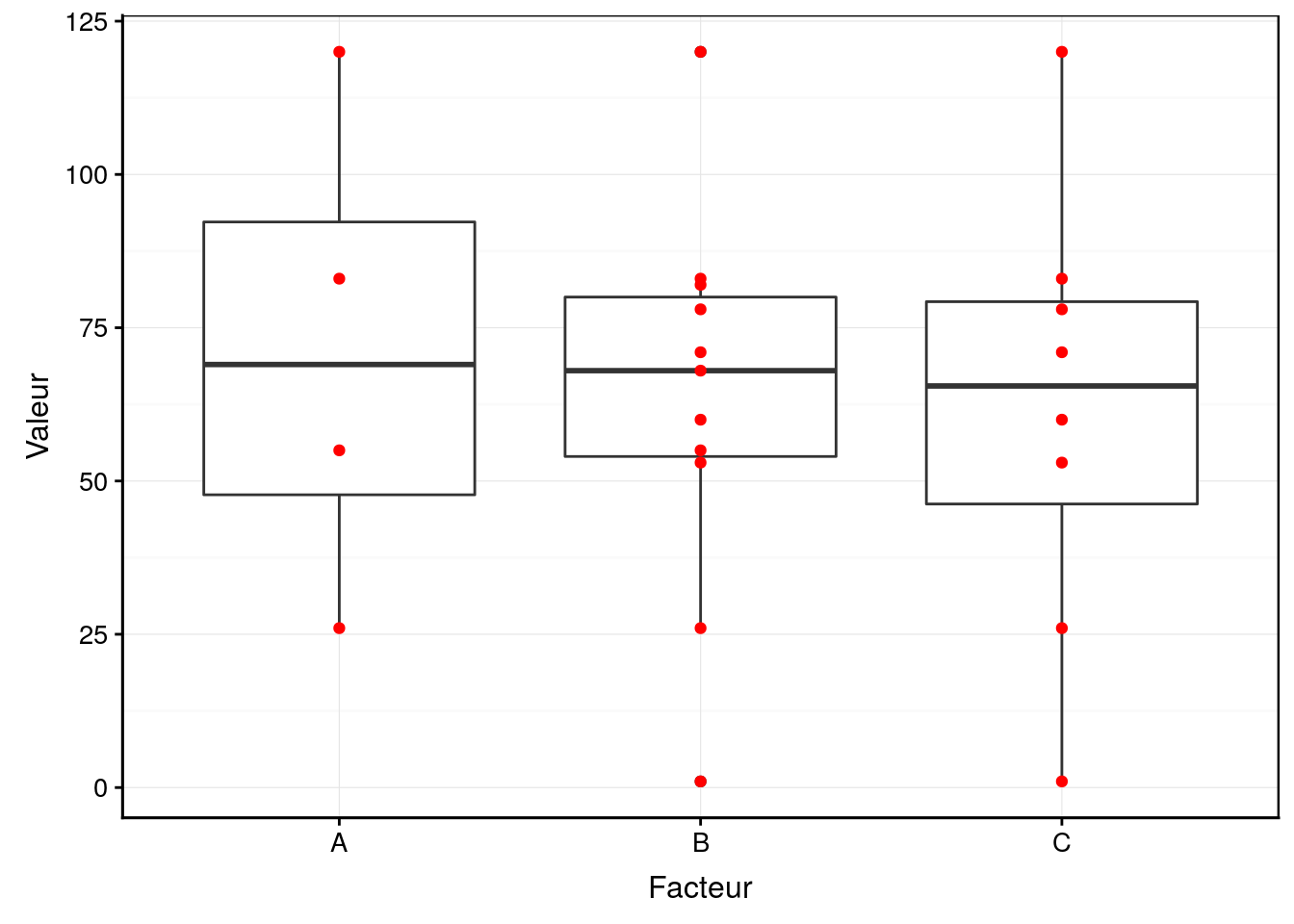
Figure 4.16: Piège des boites de dispersion : trop peu d’observations disponibles pour a.

La boite de dispersion A est calculée à partir de seulement quatre observations. C’est trop peu. Comme les points représentant les observations ne sont habituellement pas superposés à la boite, cela peut passer inaperçu et tromper le lecteur ! Une bonne pratique consiste à ajouter n, le nombre d’observations au-dessus de chaque boite. Cela peut se faire facilement avec les fonctions give_n() et stat_summary() ci-dessous.

give_n <- function(x)
  c(y = max(x) * 1.1, label = length(x)) 

chart(data = copepoda, size ~ class) +
  geom_boxplot() + 
  stat_summary(fun.data = give_n, geom = "text", hjust = 0.5)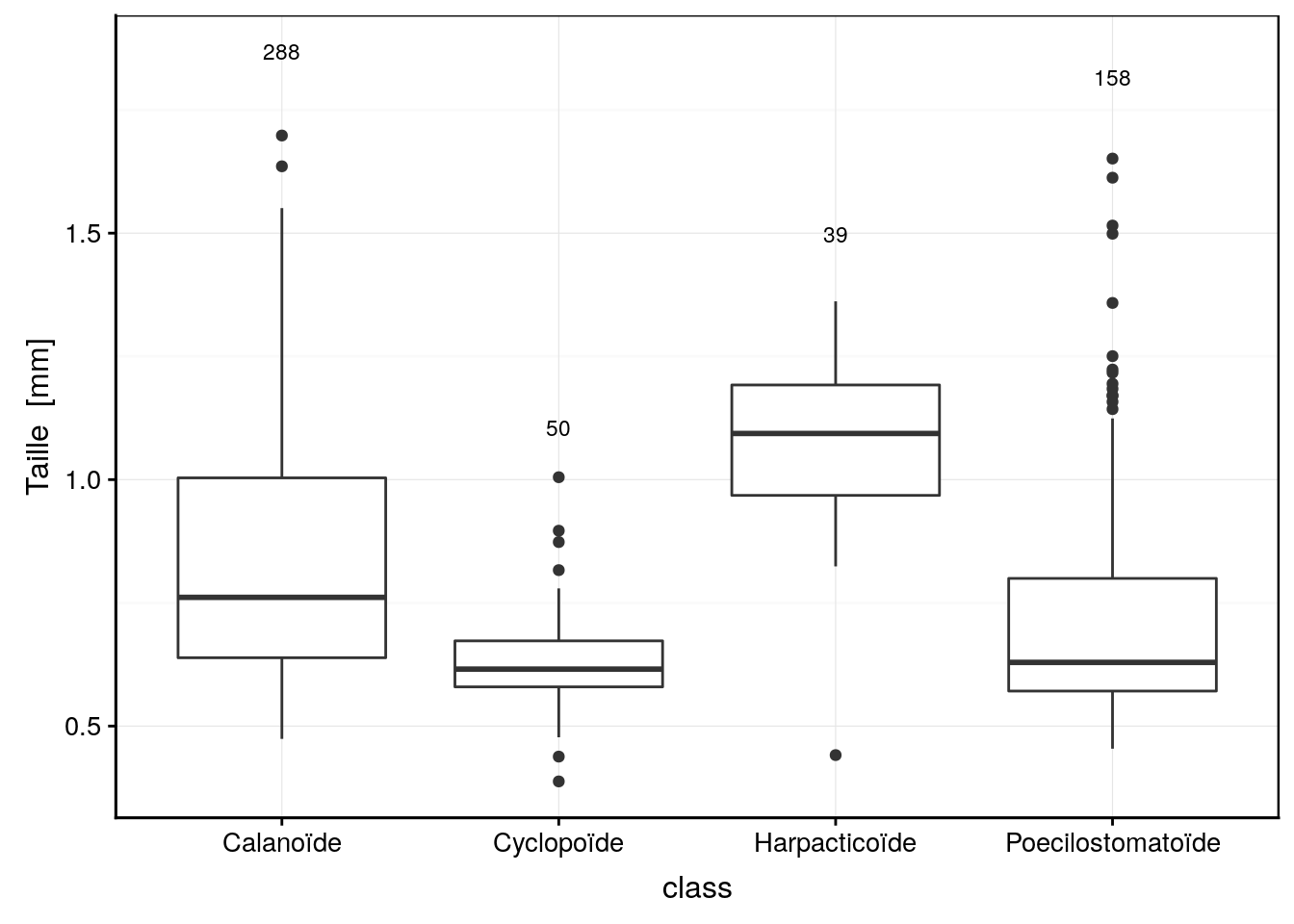

Figure 4.17: Taille de copépodes pour différents groupes taxonomiques (le nombre d’observations est indiqué au dessus de chaque boite).

4.3.2 En fonction de 2 facteurs

La Fig. 4.18 présente un graphique en boites de dispersion parallèles qui combine l’usage de deux variables facteurs différentes.

# Importation du jeu de données ToothGrowth
(tooth_growth <- read("ToothGrowth", package = "datasets"))

# # A tibble: 60 x 3
#      len supp   dose
#    <dbl> <fct> <dbl>
#  1   4.2 VC      0.5
#  2  11.5 VC      0.5
#  3   7.3 VC      0.5
#  4   5.8 VC      0.5
#  5   6.4 VC      0.5
#  6  10   VC      0.5
#  7  11.2 VC      0.5
#  8  11.2 VC      0.5
#  9   5.2 VC      0.5
# 10   7   VC      0.5
# # … with 50 more rows

# Remaniement et labelisation du jeu de données
tooth_growth$dose <- as.ordered(tooth_growth$dose)
tooth_growth <- labelise(tooth_growth, self = FALSE,
  label = list(
    len = "Longueur des dents",
    supp = "Supplémentation",
    dose = "Dose"
  ),
  units = list(
    len = "mm",
    supp = NA,
    dose = "mg/J"
  )
)
# Réalisation graphique
chart(data = tooth_growth, len ~ supp %fill=% dose) +
  geom_boxplot() +
  stat_summary(fun.data = give_n, geom = "text", hjust = 0.5,
    position = position_dodge(0.75))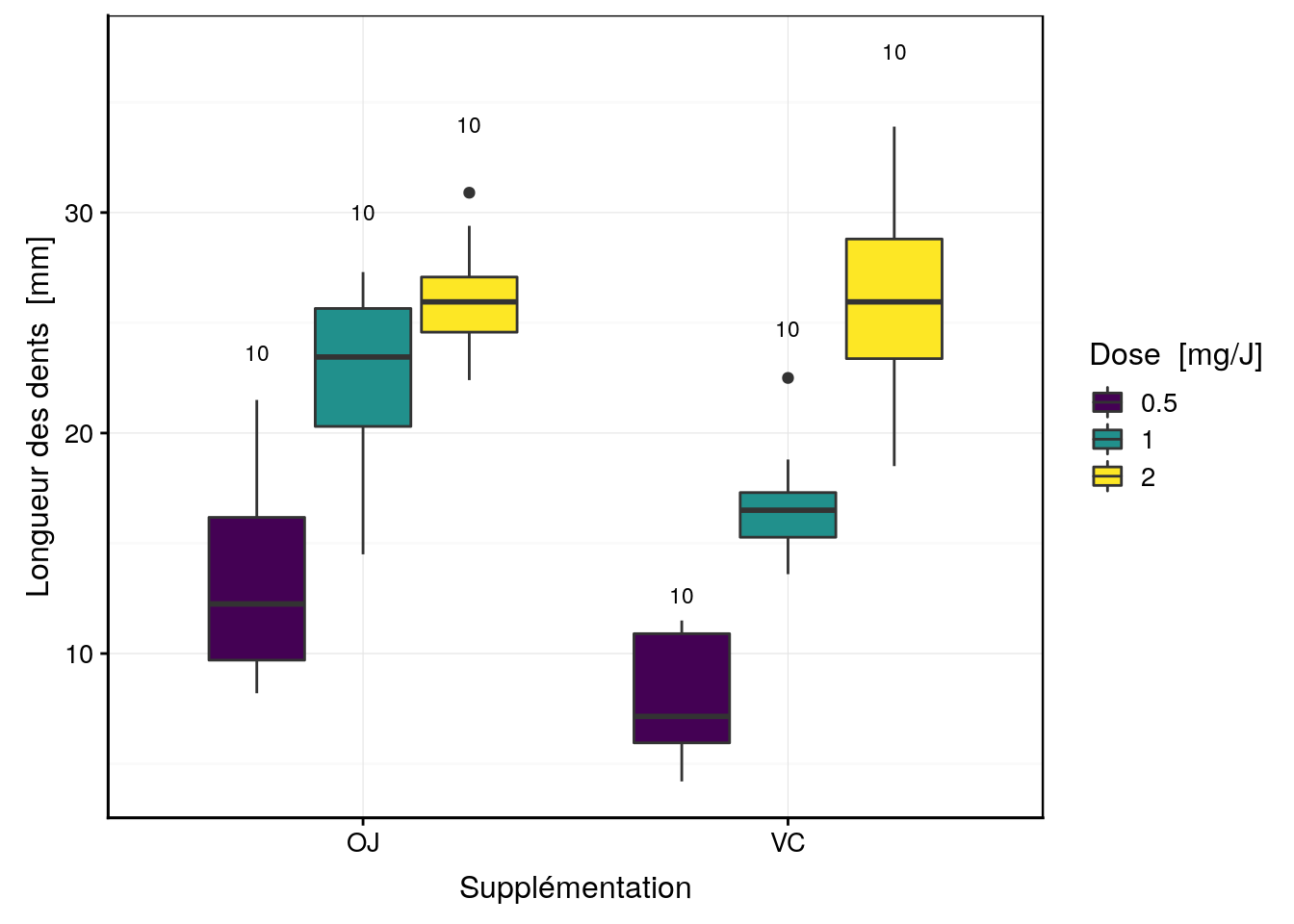

Figure 4.18: Croissance de dents de cochons d’Inde en fonction de la supplémentation (OJ = jus d’orange, VC = vitamine C) et de la dose administrée (n indiqué au dessus de chaque boite).

Pour en savoir plus

• Un tutoriel boites de dispersion à l’aide de ggplot() présentant encore bien d’autres variantes possibles.

• Box plots in ggplot2. Autre explication en anglais avec sortie utilisant plotly.

• Grouped box plots.

• Explication plus détaillée sur les cinq nombres, en anglais.

---

13. Notez que, lorsque la coupure tombe entre deux observations, une valeur intermédiaire est utilisée. Ici par exemple, le premier quartile est entre 53 et 55, donc, il vaut 54. Le troisième quartile se situe entre 78 et 82. Il vaut donc 80.↩

14. Il est possible de modifier la transparence des points et/ou de les déplacer légèrement vers la gauche ou vers la droite de manière aléatoire pour résoudre le problème de chevauchement des points sur un graphique en nuage de points univarié.↩