8.3 Métriques (étudiants de l’UMONS)
En matière de gestion des données, nous avons vu jusqu’ici comment encoder ses données dans un tableau cas par variables, comment importer des données dans R, et comment remanier les tableaux de données et les variables (numériques, tranformation en variable factor, encodage et gestion des valeurs manquantes, etc.) Toutes les variables présentes dans le tableau de départ à l’importation sont dites variables brutes… mais les possibilités ne sont pas seulement limitées à ces variables de départ.
En science des données, les variables brutes ne sont pas toujours les plus utiles par rapport aux questions que nous nous posons. Au delà de la simple transformation des données (logarithme, puissance, racine, inverse, …) pour linéariser un nuage de points, nous sommes amenés à élaborer des variables calculées ou métriques qui vont caractériser ou quantifier un aspect particulier présent dans les données.
8.3.1 Morphométrie de crabes
Partons d’un exemple concret. Le jeu de données crabs du package MASS rassemble des données relatives à la morphométrie de la carapace d’un crabe.
SciViews::R
crabs <- read("crabs", package = "MASS", lang = "fr")L’aide en ligne de ce jeu de données (voir .?crabs) nous indique qu’il s’agit de mesures réalisées sur des crabes de l’espèce Leptograpsus variegatus (Fabricius, 1793) collectés à Freemantle à l’ouest de l’Australie. Deux variétés co-existent (incorrectement libellées species dans le jeu de données) : la variété bleue (B) et la variété orange (O).

Crabe Leptograpsus variegatus variété bleue. Photo : Neville Coleman, license CC By 4.0 Museums Victoria.
Nous pouvons explorer ce jeu de données en vue de déterminer si des différences morphologiques de la carapace existent entre sexes (variable sex, soit M, soit F) ou entre variétés (variable species, soit B, soit O). Un tableau de contingence à deux entrées peut être obtenu à l’aide de la fonction table() :
table(crabs$species, crabs$sex)#
# F M
# B 50 50
# O 50 50Un snippet existe pour obtenir quelque chose de similaire (entrer ..., puis exploratory stats puis contingency, puis contingency table - 2 entries). La sortie n’est pas très belle, mais la réalisation d’un table mieux formattée nécessite pour l’instant plus de travail dans R (ne cherchez pas à retenir ce code) :
crabs %>.%
mutate(., # Changer les labels de species et sex pour des valeurs plus explicites
species = fct_recode(species, `**Variété bleue**` = "B", `**Variété orange**` = "O"),
sex = fct_recode(sex, `Femelle` = "F", Mâle = "M")
) %>.%
with(., table(species, sex)) %>.% # Tableau de contingence à 2 entrées
knitr::kable(., caption = "Nombre de crabes mesurés par variété et par sexe.",
align = "c", escape = FALSE)| Femelle | Mâle | |
|---|---|---|
| Variété bleue | 50 | 50 |
| Variété orange | 50 | 50 |
Notre échantillon est bien balancé entre les variétés et les sexes avec 100 individus pour chacun répartis en sous-groupes d’effectifs égaux (n = 50). On parle de plan balancé lorsqu’un échantillonnage stratifié a été réalisé pour s’assurer d’avoir le même nombre d’individus pour chaque niveau d’une ou plusieurs variables qualitatives, quelle que soit la proportion de ces différents niveaux dans la population de départ. C’est une situation optimale pour bien comparer les variétés et/ou les sexes ici.
Cinq mesures sont réalisées (toutes exprimées en mm) sur la carapace de ces crabes : front (taille du lobe frontal), rear (largeur à l’arrière), length (longueur), width (largeur à l’endroit le plus large) et depth (épaisseur). Il n’y a pas de valeurs manquantes dans le tableau. Aucune de ces variables morphométriques ne permet de discerner les deux variétés de couleur ou les sexes comme le montrent les cinq graphiques en violon ci-dessous.
chart(data = crabs, front ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75), trim = FALSE)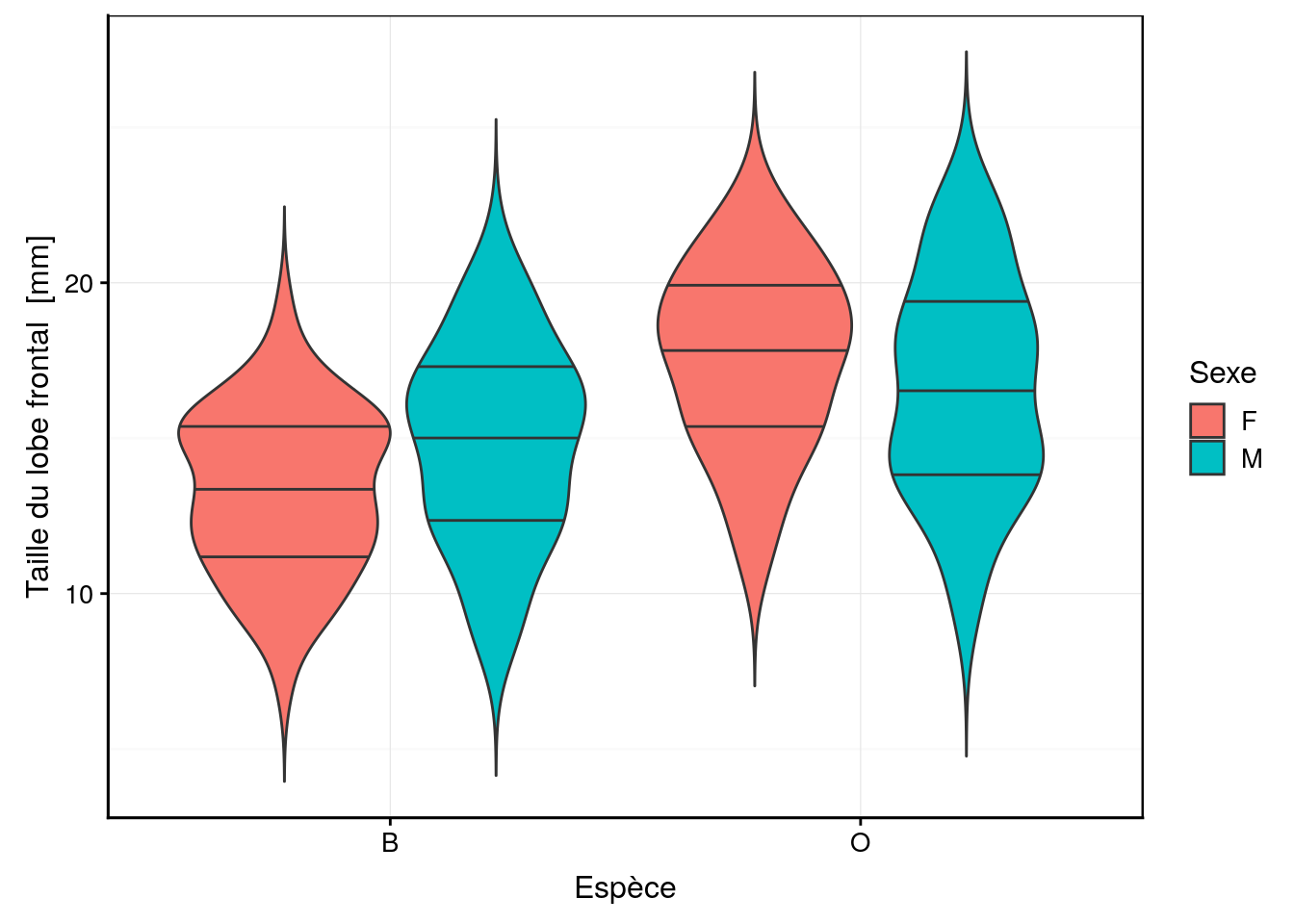
chart(data = crabs, rear ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75))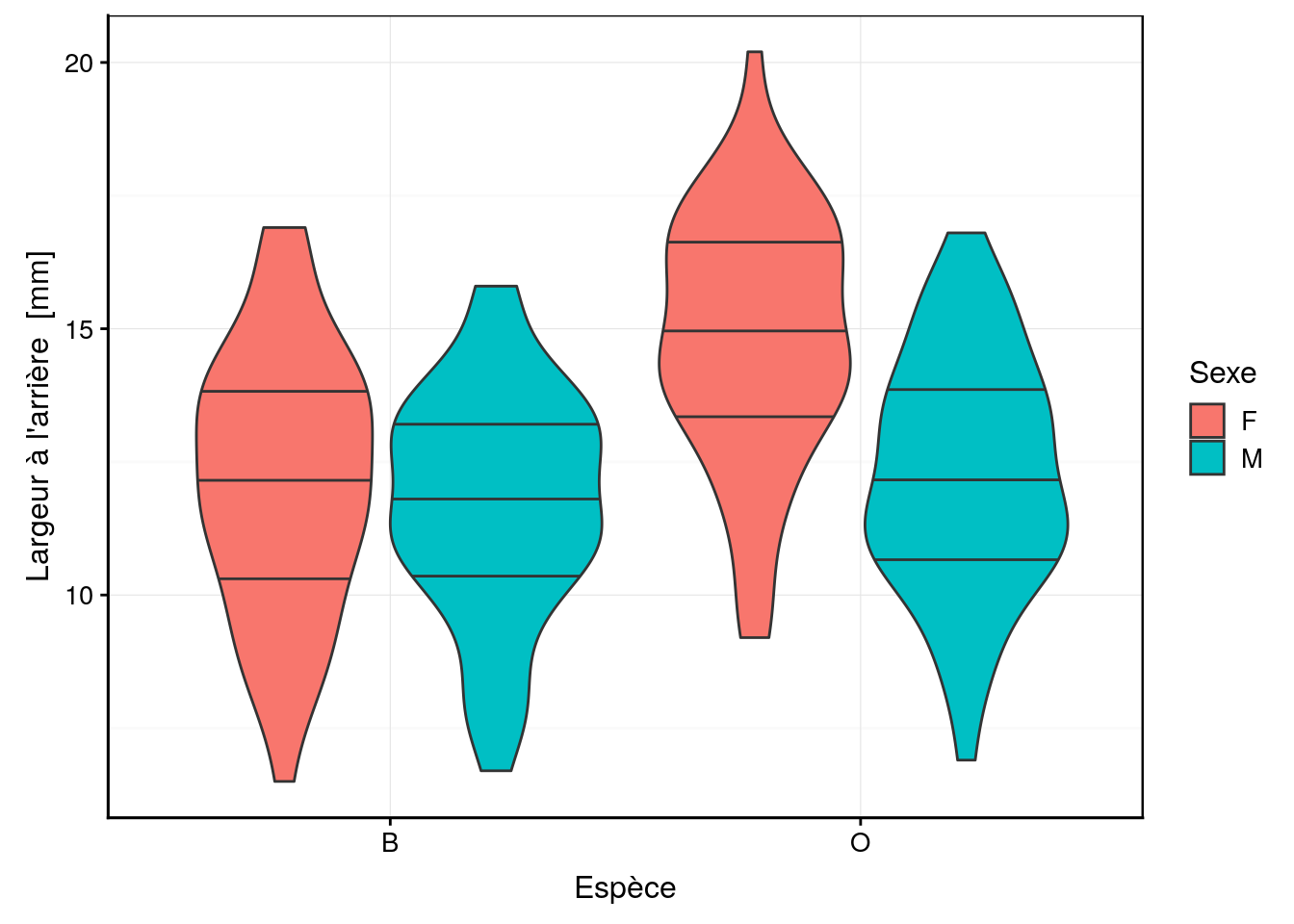
chart(data = crabs, length ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75))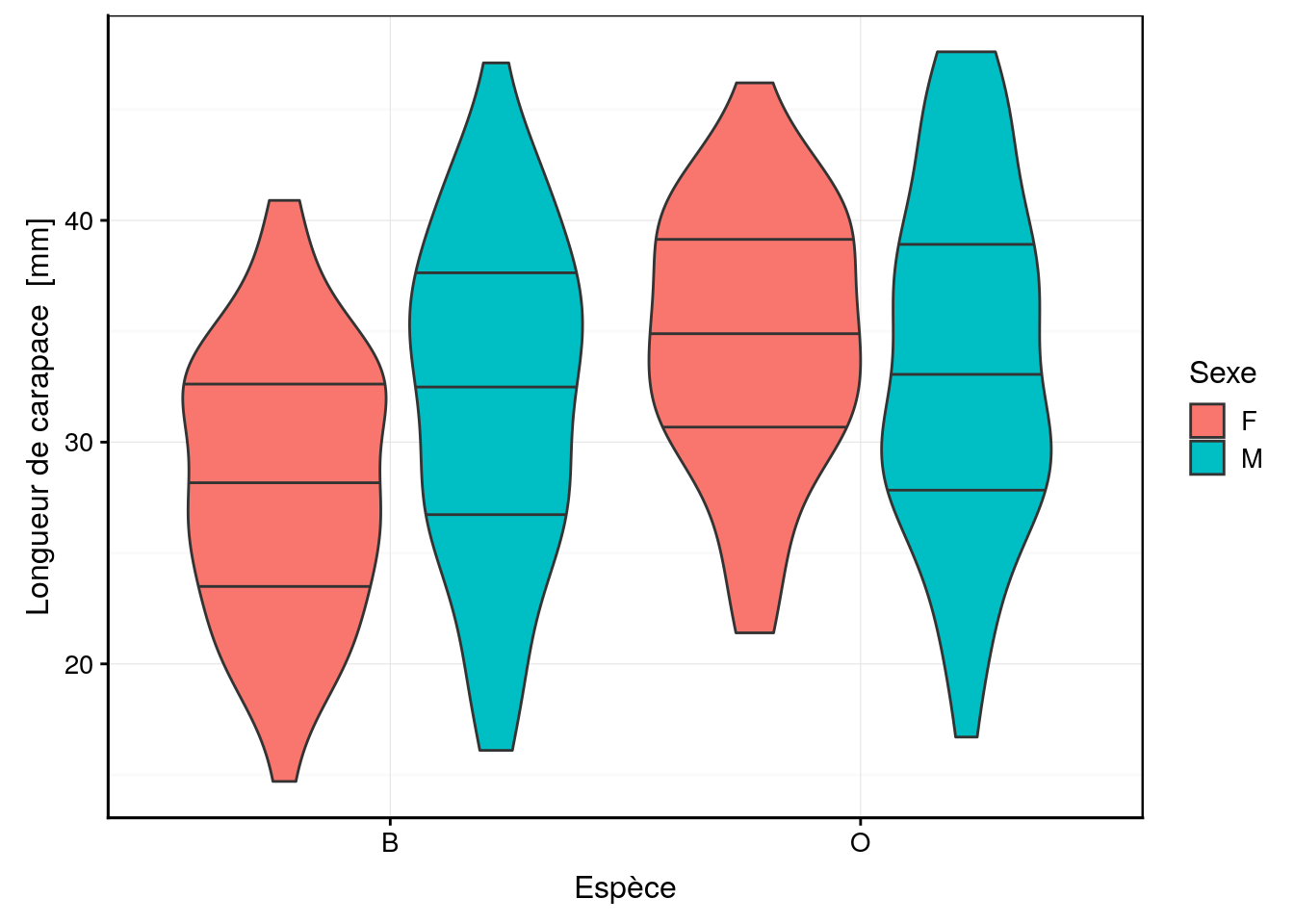
chart(data = crabs, width ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75))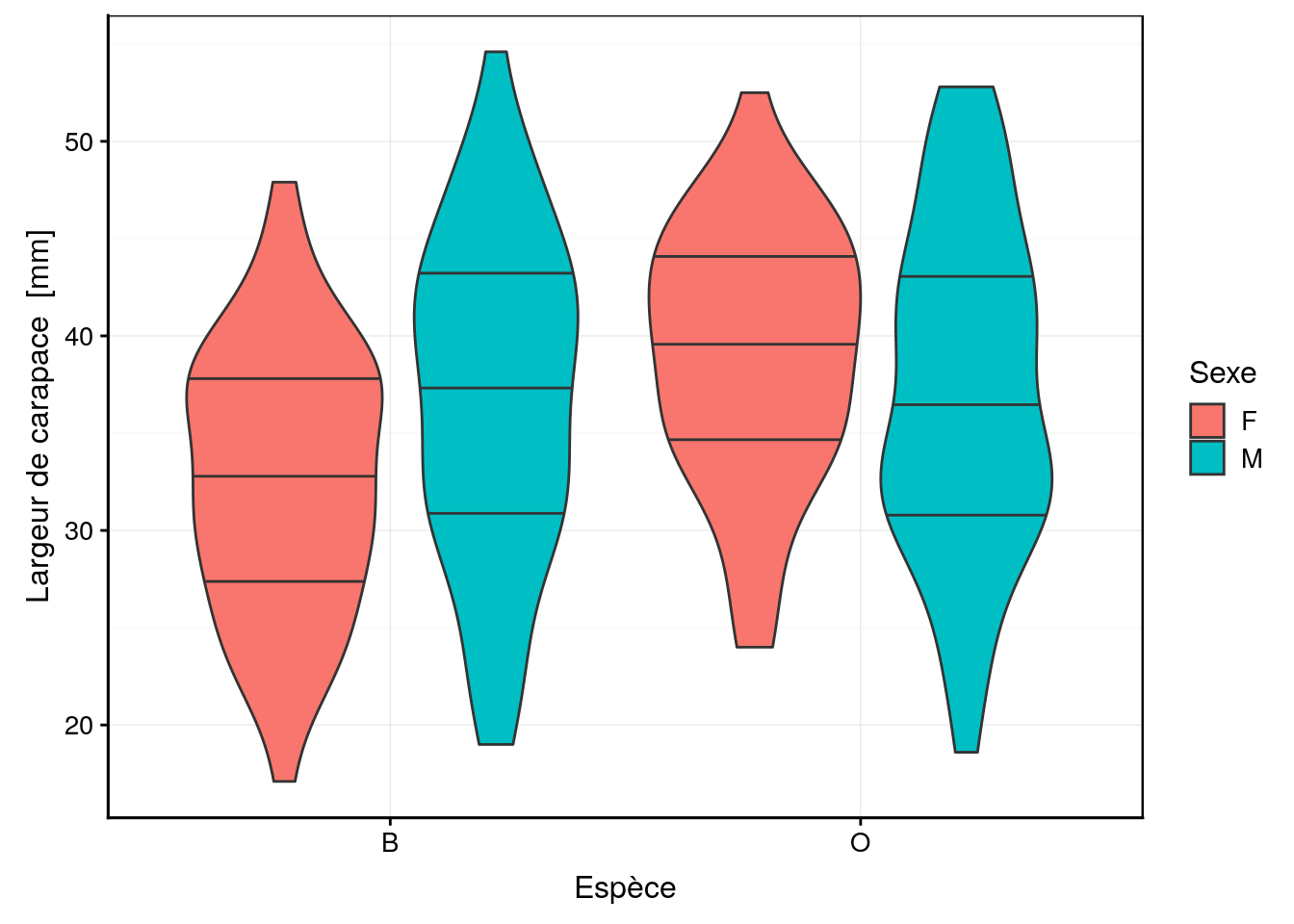
chart(data = crabs, width ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75))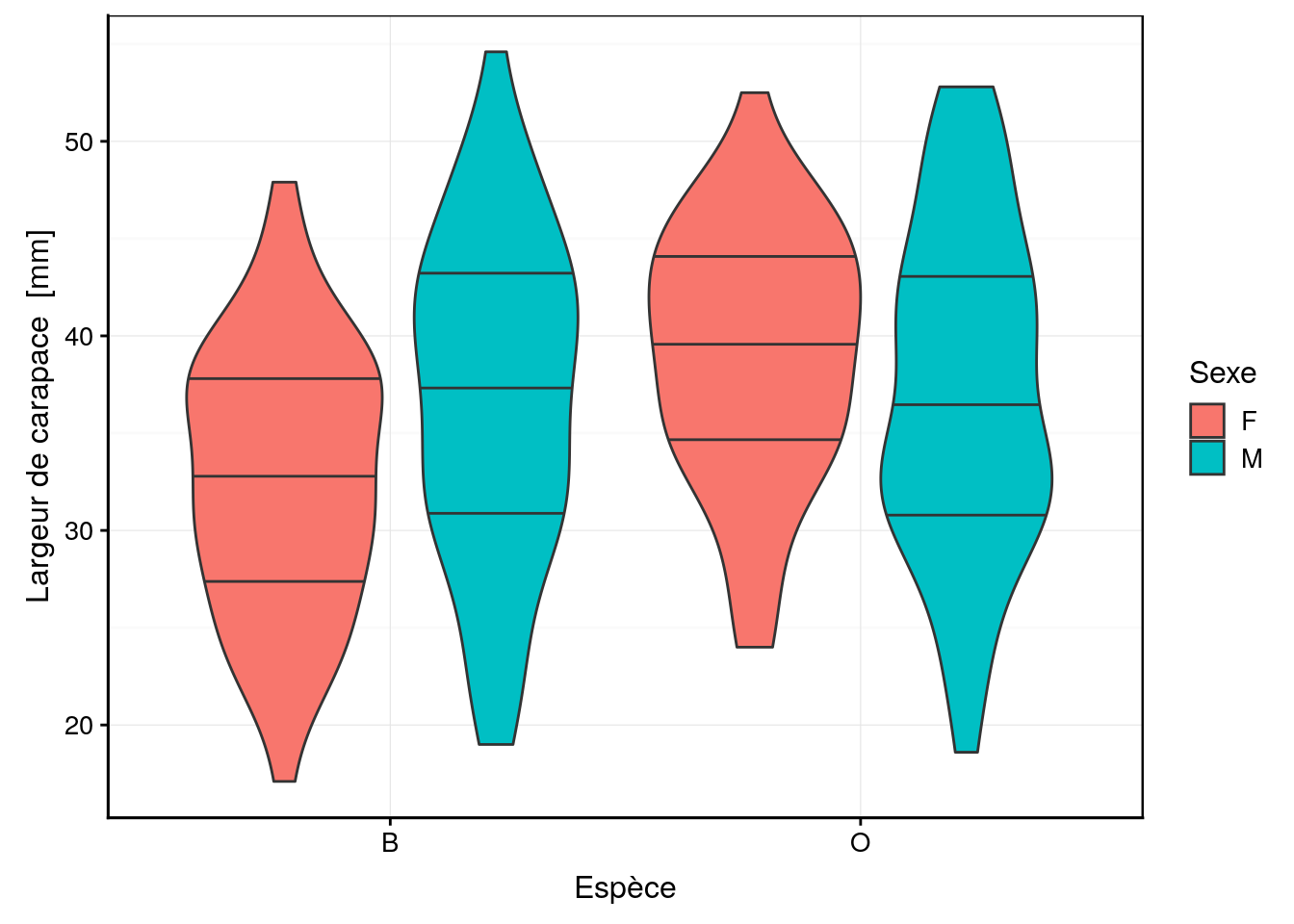
Des tendances générales peuvent être notées. Par exemple, le lobe frontal tend à être légèrement plus grand pour la variété orange, ou la largeur à l’arrière tend à être plus grande pour les femelles, surtout chez la variété orange. Cependant, aucun de ces critères ne peut être retenu pour différencier les variétés ou les espèces pour un individu en particulier car les distributions se chevauchent toutes très largement.
Nous pouvons aussi représenter des nuages de points afin de visualiser la variation d’une variable par rapport à une autre. Parmi tous les graphiques réalisables (toutes les combinaisons deux à deux des cinq variables morphologiques), examinons plus en détails les représentations suivantes :
chart(data = crabs, rear ~ length %shape=% species %col=% sex) +
geom_point()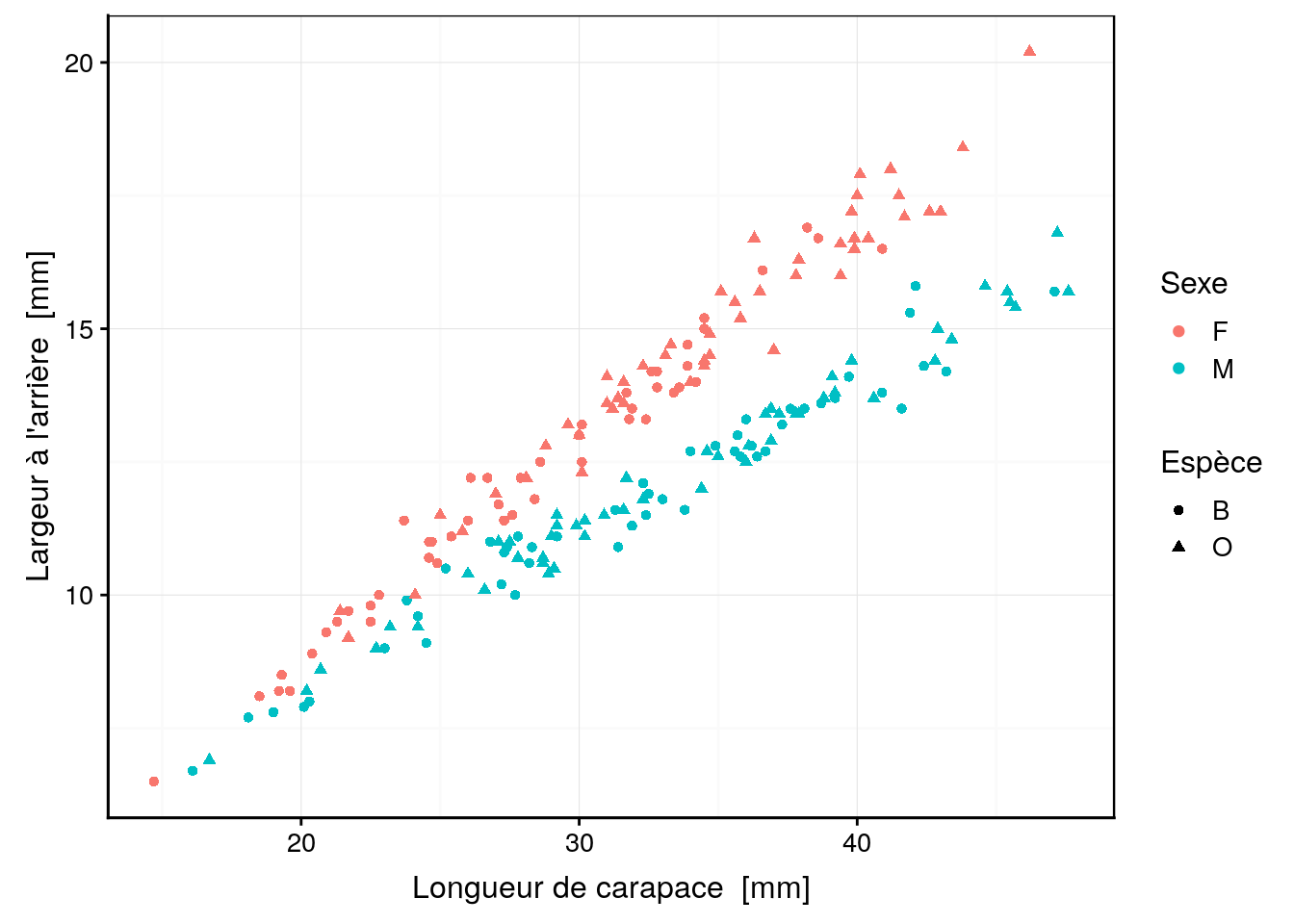
Ce graphique sépare relativement bien les mâles des femelles pour les deux variétés.
chart(data = crabs, front ~ width %shape=% species %col=% sex) +
geom_point()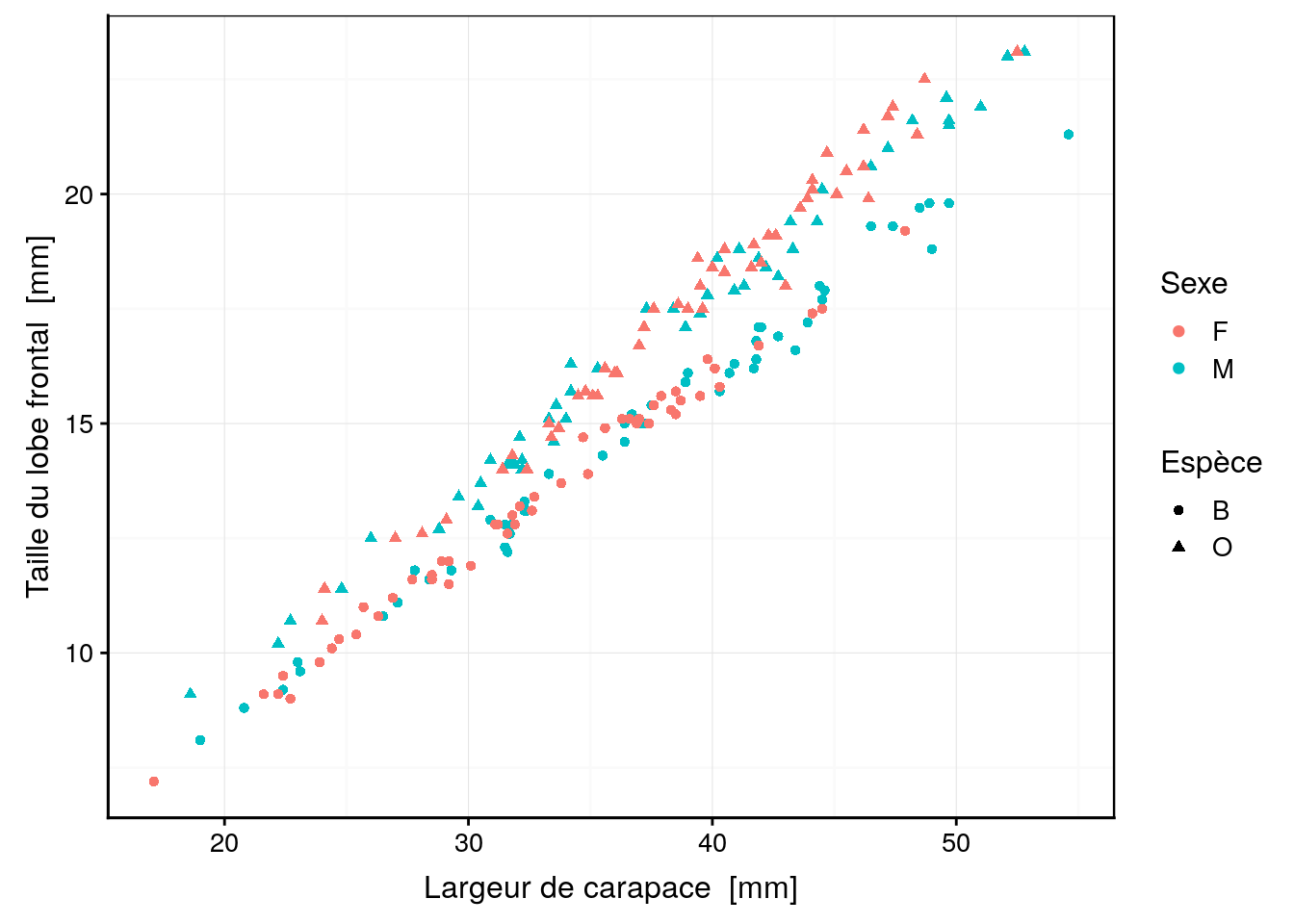
Ce graphique, en revanche, sépare les deux variétés, quel que soit leur sexe (la variété bleue en bas, et la varété orange en haut). Cela signifie donc que les données morphométriques contiennent une information permettant de discerner les sexes et les variétés, mais cette information n’est pas visible lorsqu’une seule variable quantitative est représentée en fonction des sous-populations comme dans les graphiques en violons.
En réalité, les différences de forme sont masquées sur les mesures individuelles par une variation encore plus grande liée à la taille des animaux. Comment pouvons-nous mettre en évidence un facteur de forme en faisant abstraction de la taille ? Pour expliquer cela simplement, considérons un cas facile. Imaginons que nous voulons classer un ensemble de quadrilatères à angles droits. Nous savons tous que ce sont des rectangles. Un cas particulier est le carré avec ses côtés égaux. Tant que nous représentons la longueur ou la largeur de nos quatrilatères à angles droits de toutes tailles, nous ne pouvons pas distinguer les carrés des rectangles. Par contre, si nous calculons le ratio longueur/largeur, nous faisons abstraction de la taille pour quantifier la forme (allongée ou pas). Tous les quadrilatères à angles droits dont le ratio longueur/largeur vaut un est un carré !
C’est exactement le même raisonnement que nous pouvons appliquer à nos données crabs : nous pouvons calculer des variables qui feront abstraction de la taille pour quantifier des facteurs de forme particuliers. Les femelles ayant une carapace plus large à l’arrière proportionnellement à leur taille, le ratio rear/length calculé et nommé rear_length donne ceci :
crabs %>.%
mutate(., rear_length = rear / length) %>.% # Calcul de rear_length
chart(data = ., rear_length ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75)) +
ylab("Ratio largeur arrière/longueur")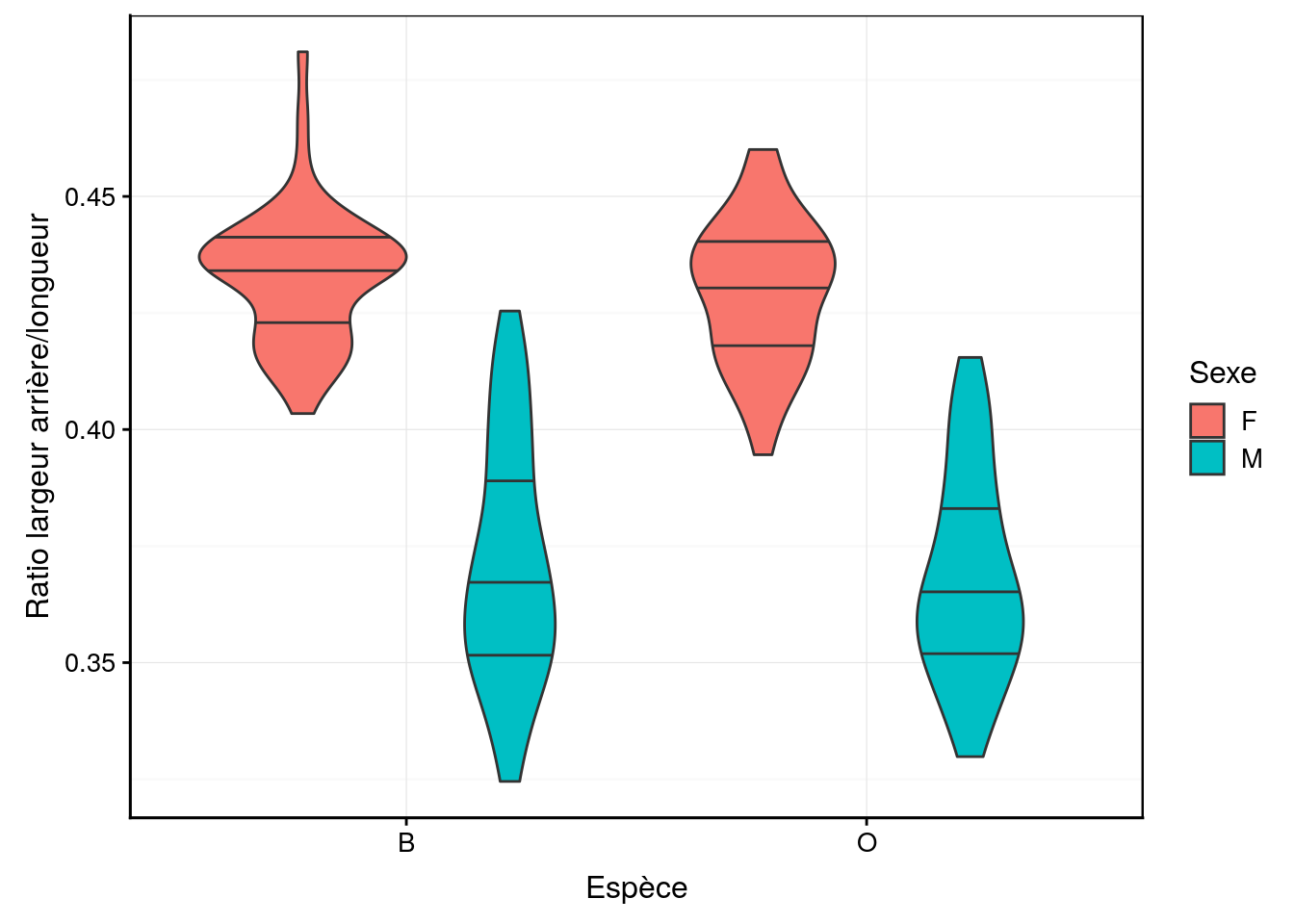
Notre métrique rear_length est naturellement ultra-simple. Elle ne permet pas de différencier tous les mâles de toutes les femelles, mais la séparation est déjà bien meilleure qu’en utilisant soit rear soit length seuls. A l’aide de techniques statistiques que vous étudierez au cours de science des données biologiques II l’an prochain, nous pouvons montrer qu’une meilleure métrique (ou indice) pour séparer les mâles des femelles est en réalité : rear / (0.3 * length + 2.4)41. La séparation entre les sexes n’est pas totale, mais s’en rapproche fortement, surtout pour la variété orange.
crabs %>.%
mutate(., rear_length2 = rear / (0.3 * length + 2.4)) %>.% # Calcul de rear_length2
chart(data = ., rear_length2 ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75)) +
ylab("Ratio largeur arrière/(0.3*longueur + 2.4)")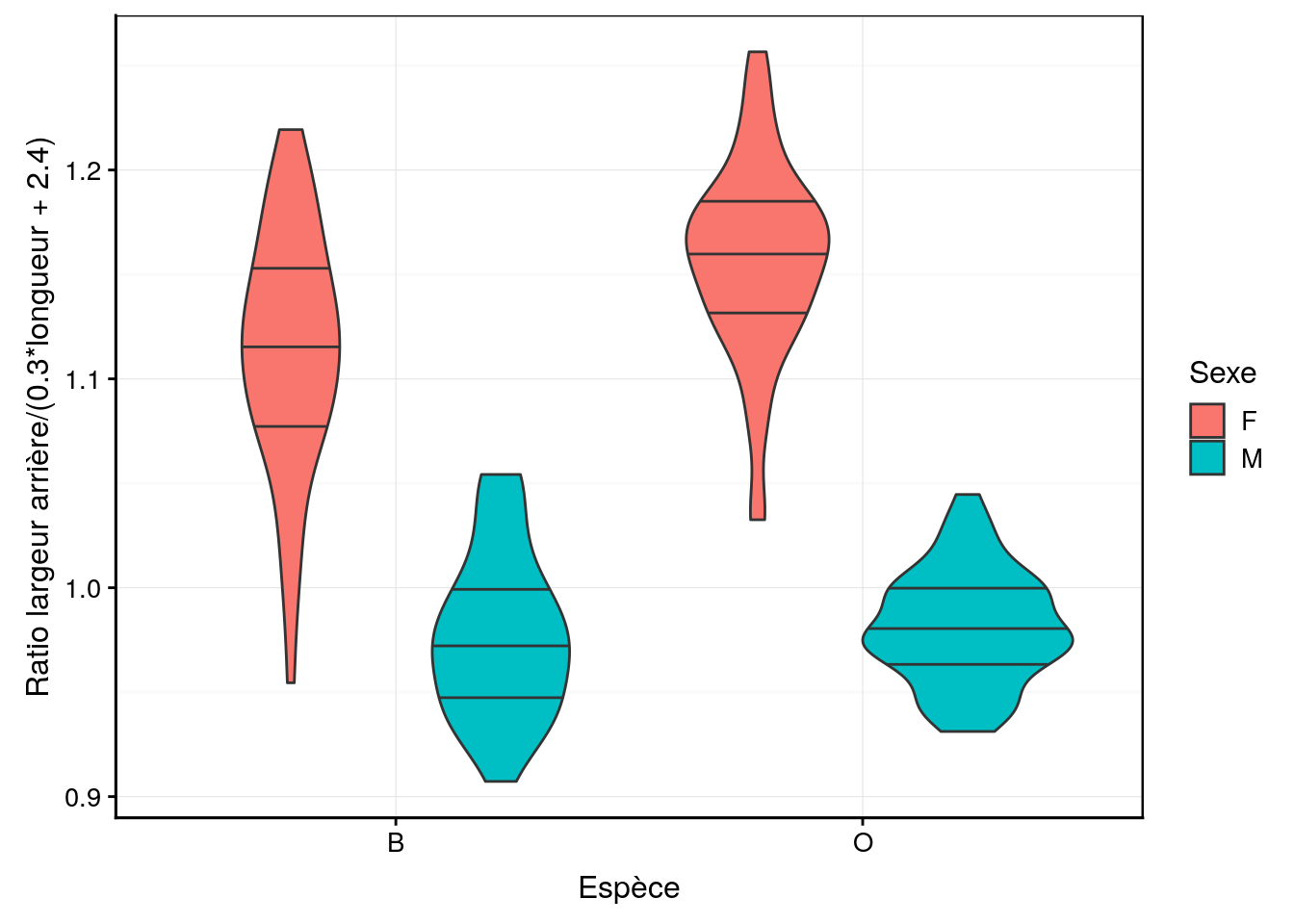
De même, nous pouvons utiliser l’indice front_width = front / (0.43 * width) pour séparer les variétés qui donne ceci :
crabs %>.%
mutate(., front_width = front / (0.43 * width)) %>.% # Calcul de front_width
chart(data = ., front_width ~ species %fill=% sex) +
geom_violin(draw_quantiles = c(0.25, 0.5, 0.75)) +
ylab("Ratio lobe frontal/(0.43*largeur)")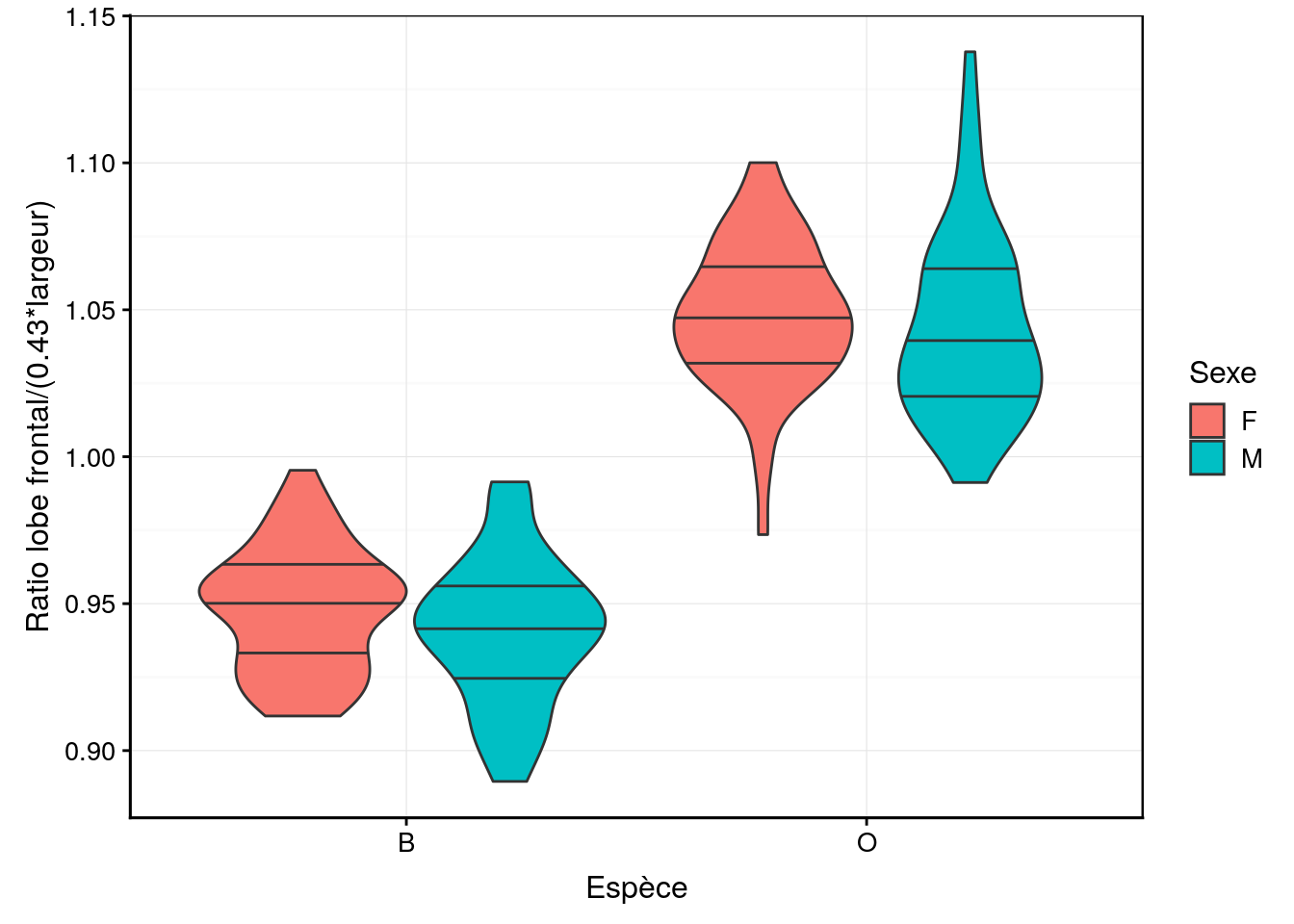
Avec cette nouvelle variable calculée, nous pouvons séparer pratiquement parfaitement les crabes de la variété orange de ceux de la variété bleue sur base uniquement de la forme de la carapace. Admettons que le critère de couleur ne soit pas fiable à 100% avec des individus pouvant arborer des colorations intermédiaires qui rendent la discrimination des variétés sur base uniquement du criètre de couleur hazardeuse. Si c’est le cas, notre indice front_width est très utile pour séparer ces variétés ou en tous cas, pour aider à le faire.
Les variables calculées transforment les données brutes pour les rendre plus utilisables dans le cadre d’analyses statistiques. C’est un processus utile et important. Elles permettent de calculer des indices, des ratios, des attributs, … qui mettent en évidence une partie de l’information contenue dans les données de départ, mais mal exprimée au niveau des variables brutes individuelles.
Les tranformations de variables (logarithme, puissances, racines, fonction inverse, …) constituent une “famille de calculs” que nous pouvons appliquer pour rendre les données plus facile à traiter, typiquement pour linéariser un nuage de points curvilinéaire, ou pour transformer une distribution log-Normale en distribution Normale.
Les métriques sont des variables issues de calculs plus complexes et qui visent à faire émerger une propriété particulièrement intéressante en rapport avec une question que nous nous posons. Bien définir et calculer des métriques est un art complexe, mais c’est aussi la clé d’une bonne analyse. La capacité à définir correctement ses métriques distingue un bon scientifique des données de quelqu’un qui utilise les outils statistiques de manière machinale sans réfléchir suffisamment à ce qu’il fait.
Devenez une/une bon(ne) scientifique des données : créez et utilisez des métriques adéquates le plus souvent possible.
8.3.2 Biométrie humaine
Le jeu de données sur la biométrie humaine que vous avez vous-mêmes réalisé est un fantastique terrain de jeu pour définir des métriques. La question centrale étant ici d’étudier la question de l’obésité, les métriques les plus importantes sont celles qui permettent de bien quantifier cela.
Rappelons nous que nous avons déjà utilisé une métrique avec l’imc et les différentes classes proposées par l’OMS.
Prenons le jeu de données biometry du package BioDataScience comme exemple.
biometry <- read("biometry", package = "BioDataScience", lang = "FR") %>.%
select(., height, weight)
biometry# # A tibble: 395 x 2
# height weight
# <dbl> <dbl>
# 1 182 69
# 2 190 74
# 3 185 83
# 4 175 60
# 5 167 48
# 6 179 52
# 7 167 72
# 8 180 74
# 9 189 110
# 10 160 82
# # … with 385 more rowsL’utilisation d’un nuage de points de la taille en fonction de la masse ne nous permet pas de quantifier l’obésité au sein de notre échantillon comme le montre le graphique ci-dessous :
chart(biometry, height ~ weight) +
geom_point()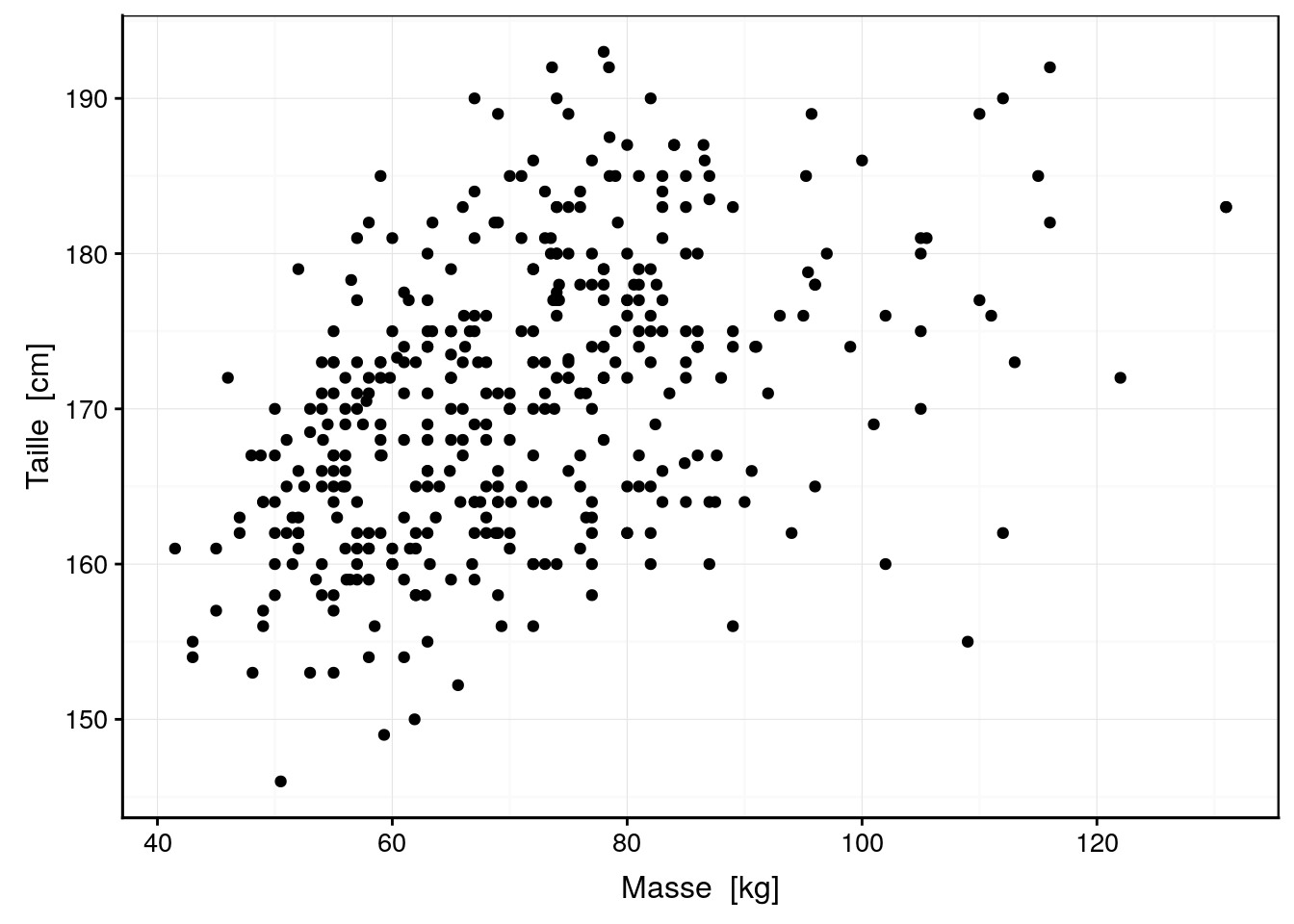
L’utilisation de l’IMC comme indice afin de quantifier l’obésité est bien plus intéressant.
biometry %>.%
mutate(.,
bmi = weight / (height / 100)^2,
bmi_schedule = case_when(
bmi < 18.5 ~ "sous-poids",
bmi >= 18.5 & bmi < 25 ~ "poids normal",
bmi >= 25 & bmi < 30 ~ "surpoids",
bmi >= 30 ~ "obèse"),
bmi_schedule = factor(
bmi_schedule,
levels = c("sous-poids", "poids normal", "surpoids", "obèse"),
ordered = TRUE)
) -> biometry
biometry# # A tibble: 395 x 4
# height weight bmi bmi_schedule
# <dbl> <dbl> <dbl> <ord>
# 1 182 69 20.8 poids normal
# 2 190 74 20.5 poids normal
# 3 185 83 24.3 poids normal
# 4 175 60 19.6 poids normal
# 5 167 48 17.2 sous-poids
# 6 179 52 16.2 sous-poids
# 7 167 72 25.8 surpoids
# 8 180 74 22.8 poids normal
# 9 189 110 30.8 obèse
# 10 160 82 32.0 obèse
# # … with 385 more rowsLe graphique en barres de l’imc est plus intéressant que le graphique précendent afin de mettre en avant les individus obèses.
chart(biometry, ~ bmi_schedule) +
geom_bar() +
labs(x = "Echelle de l'IMC", "Dénombrement")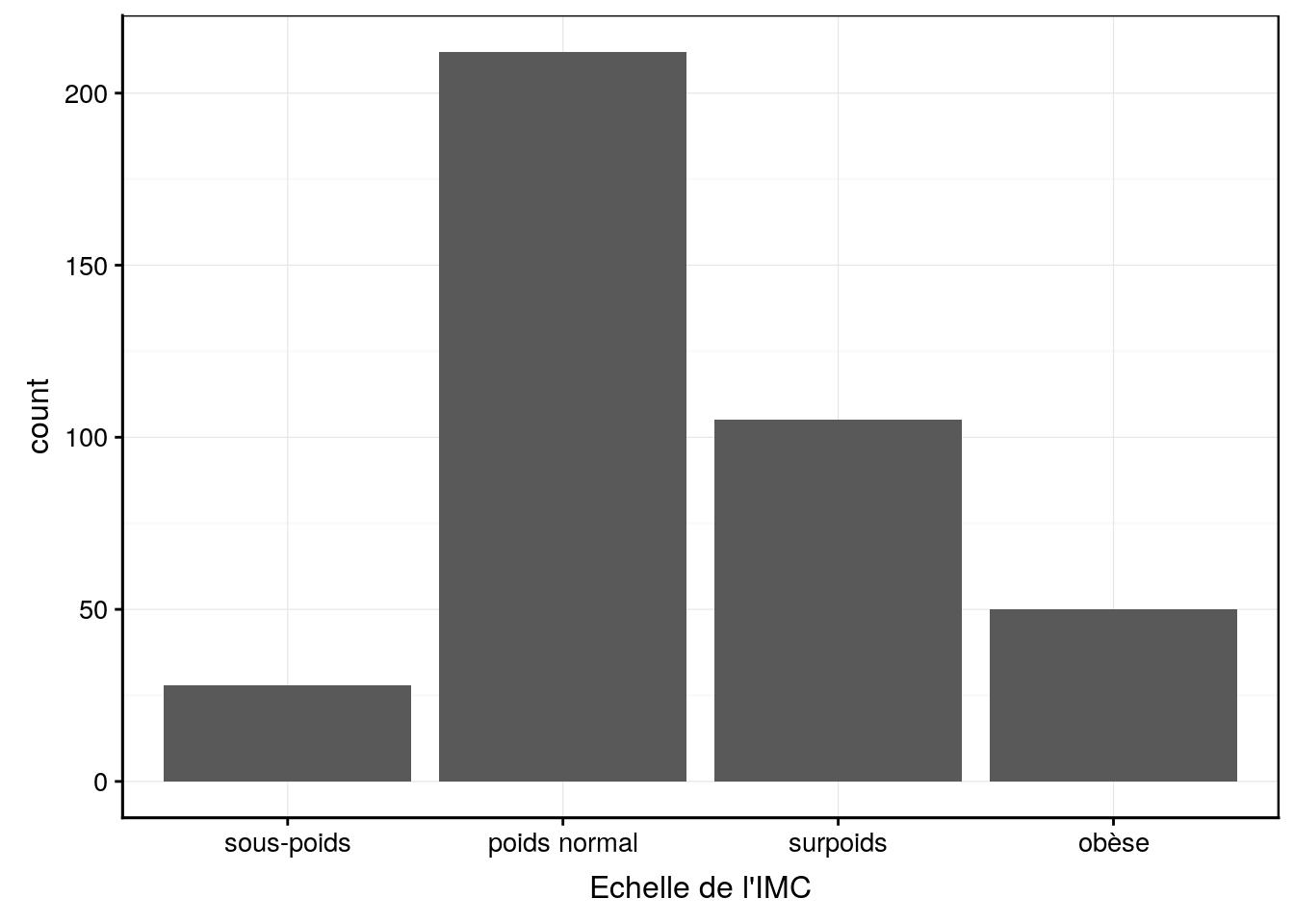
A vous de jouer !
Dans le projet portant sur le biométrie humaine, réalisez les instructions proposées via le lien suivant :
https://github.com/BioDataScience-Course/sdd_lesson/blob/2019-2020/sdd1_08/presentations/indices.md
Afin de vous aider dans la recherche d’indices intéressants et pertinents, des documents sont mis à votre disposition via le lien suivant:
https://github.com/BioDataScience-Course/sdd_lesson/tree/2019-2020/sdd1_08/biometry_doc_supp
Débutez votre recherche d’indice avec la lecture de l’article : Comment mesurer la corpulence et le poids idéal ? Histoire, intérêts et limites de l’indice de masse corporelle
Pour le lecteur plus avancé, il s’agit en fait de la droite de régression ajustée dans le nuage de points.↩