10.1 Le danger des tests multiples

Les tests t de Student et de Wilcoxon sont limités à la comparaison de deux populations. Poursuivons notre analyse des crabes L. variegatus. Rappelez-vous, nous avons deux variétés (variable species, B pour bleue et Opour orange). Si nous voulons comparer simultanément les mâles et les femelles des deux variétés, cela nous fait quatre sous-populations à comparer (nous utilisons ici la fonction paste() qui rassemble des chaînes de caractère avec trait comme caractère séparateur sep ="-" pour former une variable facteur à quatre niveaux, B-F, B-M, O-F, O-M). Nous transformaons cette variable en facteur à l’aide de factor() et nous ajoutons un label avec labelise().

crabs <- read("crabs", package = "MASS", lang = "fr")
crabs %>.%
  mutate(., group  = labelise(
    factor(paste(species, sex, sep = "-")),
    "Groupe espèce - sexe", units = NA)) ->
  crabs2

La Fig. 10.1 montre la largeur à l’arrière de la carapace chez les quatre groupes ainsi individualisés. Une représentation graphique adéquate avant de réaliser notre analyse ici lorsque le nombre de répliquats est important est le graphique en violon sur lequel nous superposons au moins les moyennes, et de préférence, les points également. Si le nombre de répliquats est plus faible, mais toujours supérieur à 7-8, nous pourrions utiliser le même type de graphique mais avec des boites de dispersion plutôt (voir plus loin, Fig. 10.4). Avec encore moins de répliquats nous présenterons les points et les moyennes uniquement.

chart(data = crabs2, rear ~ group) +
  geom_violin() +
  geom_jitter(width = 0.05, alpha = 0.5) +
  geom_point(data = group_by(crabs2, group) %>.%
    summarise(., means = mean(rear, na.rm = TRUE)),
    f_aes(means ~ group), size = 3, col = "red")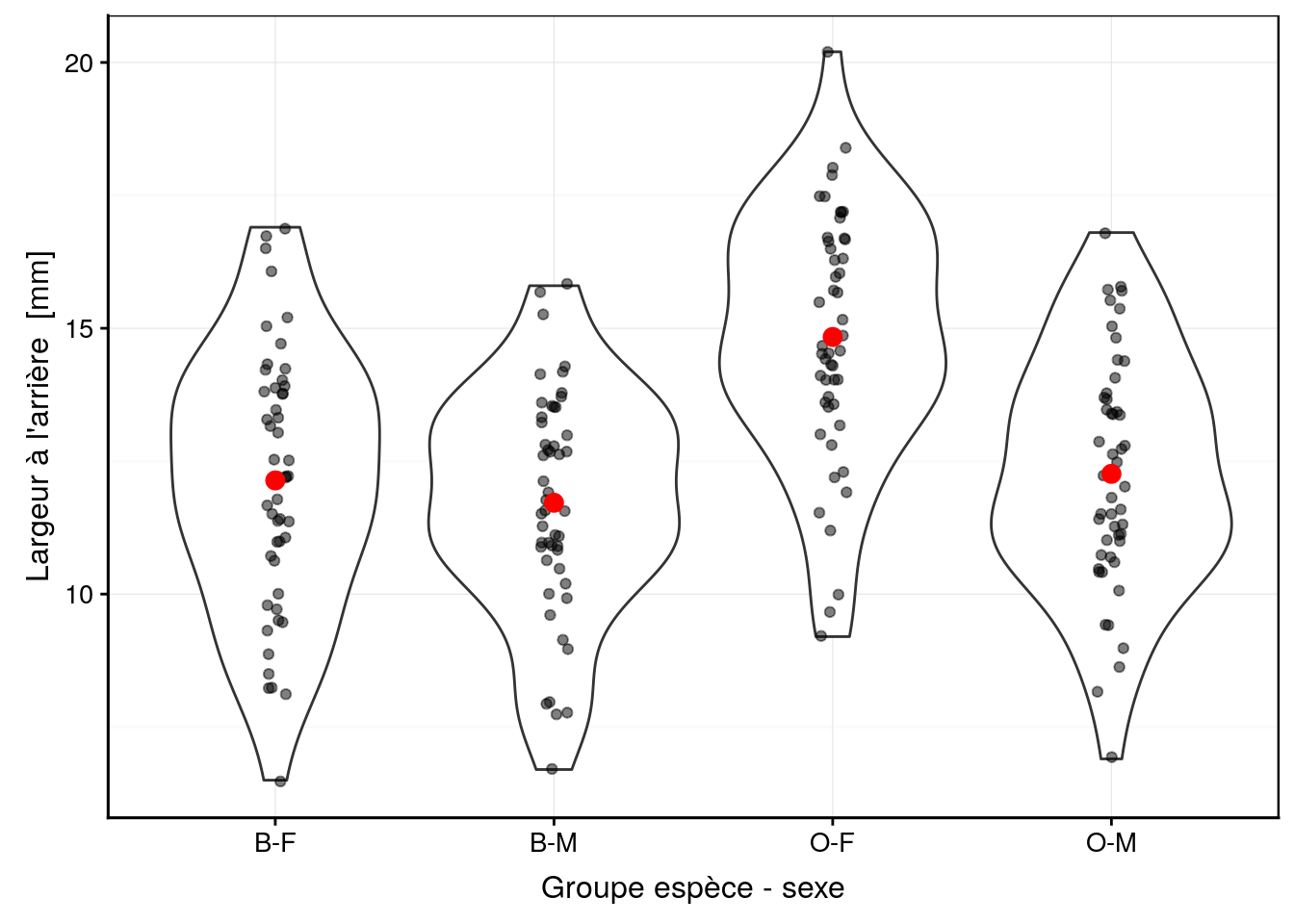
Largeur arrière en fonction du groupe de crabes *L. variegatus*. Graphique adéquat pour comparer les moyennes et distributions dans le cas d'un nombre important de répliquats (moyennes en rouge + observations individuelles en noir semi-transparent superposées à des graphiques en violon).

Figure 10.1: Largeur arrière en fonction du groupe de crabes L. variegatus. Graphique adéquat pour comparer les moyennes et distributions dans le cas d’un nombre important de répliquats (moyennes en rouge + observations individuelles en noir semi-transparent superposées à des graphiques en violon).

Nous en profitons également pour essayer l’astuce proposée au module précédent. Au lieu de travailler sur la variable rear seule, nous allons étudier l’aspect ratio entre largeur à l’arrière (rear) et largeur maximale (width) de la carapace afin de nous débarrasser d’une source de variabilité triviale qui est qu’un grand crabe est grand partout, et de même un petit crabe est petit pour toutes ses mesures. Nous prenons soin également de libeller cette nouvelle variable correctement avec labelise(). Enfin, nous ne conservons que les variables species, sex, group et aspect avec `select() :

crabs2 %>.%
  mutate(., aspect = labelise(
    as.numeric(rear / width),
    "Ratio largeur arrière / max", units = NA)) %>.%
  select(., species, sex, group, aspect) ->
  crabs2
skimr::skim(crabs2)
# Skim summary statistics
#  n obs: 200 
#  n variables: 4 
# 
# ── Variable type:factor ───────────────────────────────────────────────────────────────────────────────────────────────
#  variable missing complete   n n_unique                         top_counts
#     group       0      200 200        4 B-F: 50, B-M: 50, O-F: 50, O-M: 50
#       sex       0      200 200        2              F: 100, M: 100, NA: 0
#   species       0      200 200        2              B: 100, O: 100, NA: 0
#  ordered
#    FALSE
#    FALSE
#    FALSE
# 
# ── Variable type:numeric ──────────────────────────────────────────────────────────────────────────────────────────────
#  variable missing complete   n mean   sd   p0  p25  p50  p75 p100     hist
#    aspect       0      200 200 0.35 0.03 0.28 0.32 0.36 0.38 0.41 ▂▅▅▃▅▇▆▁

Nous avons 50 individus dans chacun des quatre groupes. Lorsqu’il y a le même nombre de réplicats dans tous les groupes, on appelle cela un plan balancé. C’est une situation optimale. Nous devons toujours essayer de nous en rapprocher le plus possible car, si le nombre d’individus mesurés diffère fortement d’un groupe à l’autre, nous aurons forcément moins d’information disponible dans le ou les groupes moins nombreux, ce qui déforcera notre analyse.

Nous voyons également que la variable aspect semble avoir une distribution bimodale d’après le petit histogramme représenté dans le résumé. La Fig. 10.2 avec aspect montre une différence plus qu'avecrear` seul, à la Fig. @ref(fig:crabs_rear).

chart(data = crabs2, aspect ~ group) +
  geom_violin() +
  geom_jitter(width = 0.05, alpha = 0.5) +
  geom_point(data = group_by(crabs2, group) %>.%
    summarise(., means = mean(aspect, na.rm = TRUE)),
    f_aes(means ~ group), size = 3, col = "red")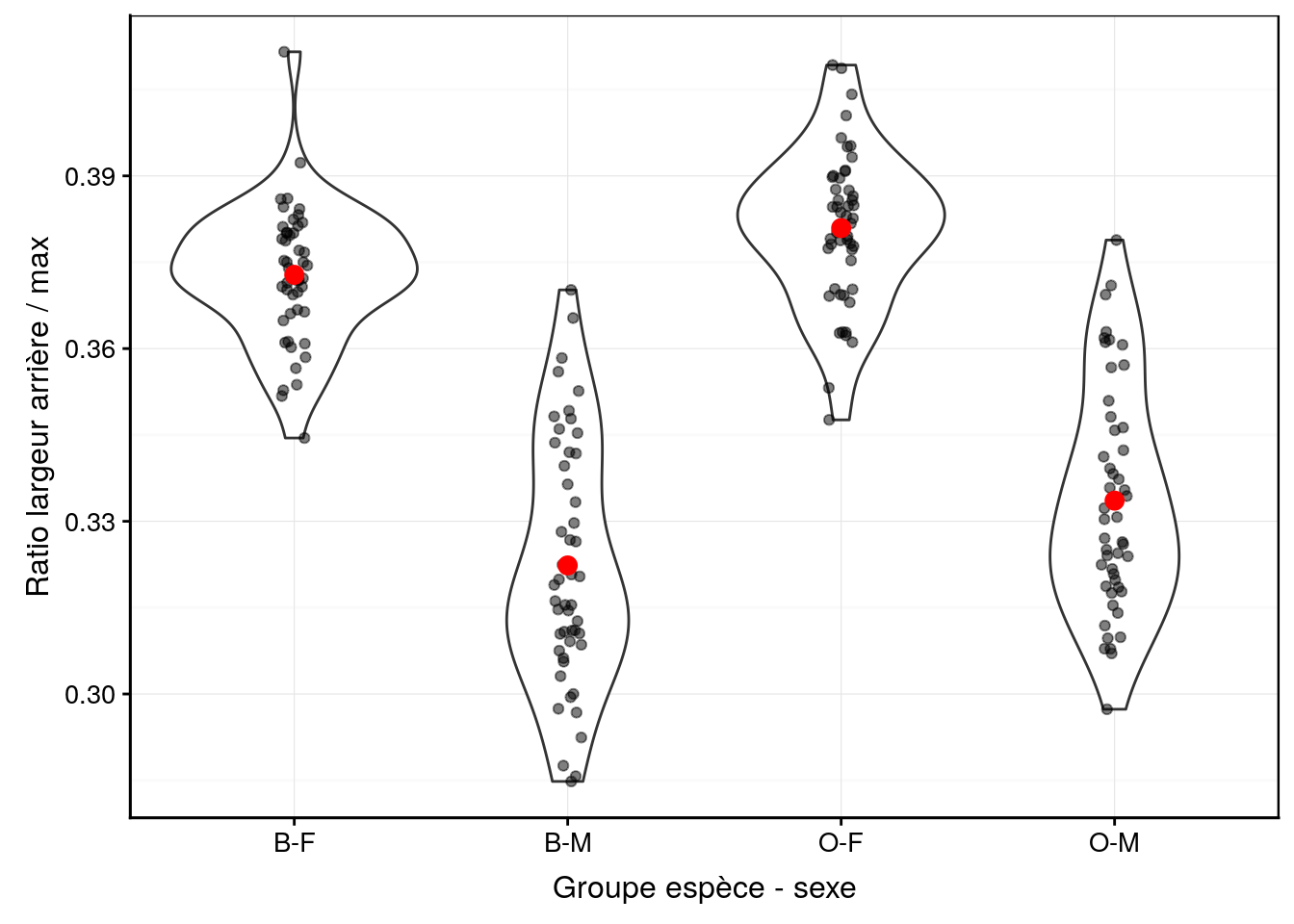
Ratio largeur arrière/largeur max en fonction du groupe de crabes *L. variegatus*. Graphique adéquat pour comparer les moyennes et distributions dans le cas d'un nombre important de répliquat (moyennes en rouge + observations individuelles en noir semi-transparent superposées à des graphiques en violon).

Figure 10.2: Ratio largeur arrière/largeur max en fonction du groupe de crabes L. variegatus. Graphique adéquat pour comparer les moyennes et distributions dans le cas d’un nombre important de répliquat (moyennes en rouge + observations individuelles en noir semi-transparent superposées à des graphiques en violon).

Nous voyons ici beaucoup mieux que la distribution bimodale est essentiellement dûe au dymorphiqme sexuel plutôt qu’à des différences entre les variétés, mais qu’en est-il plus précisément car si nous regardons attentivement, il semble que les moyennes pour les crabes bleus sont légèrement inférieures à ces des crabes oranges.

Comment comparer valablement ces quatre groupes ? Comme nous savons maintenant comparer deux groupes à l’aide d’un test t de Student, il est tentant d’effectuer toutes les comparaisons deux à deux et de résumer l’ensemble, par exemple, dans un tableau synthétique. Ca fait quant même beaucoup de comparaisons (B-F <-> B-M, B-F <-> O-F, B-F <-> O-M, B-M <-> O-F, B-M<-> O-M, et finalement O-F <-> O-M). Cela fait six comparaisons à réaliser.

N’oublions pas que, à chaque test, nous prenons un risque de nous tromper. Le risque de se tromper au moins une fois dans l’ensemble des tests est alors décuplé en cas de tests multiples. Prenons un point de vue naïf, mais qui suffira ici pour démontrer le problème qui apparaît. Admettons que le risque de nous tromper est constant, que nous rejettons ou non \(H_0\), et qu’il est de l’ordre de 10% dans chaque test individuellement49. La seule solution acceptable est que tous les tests soeijnt corrects. Considérant chaque interprétation indépendante, nous pouvons multiplier les probabilités d’avoir un test correct (90%) le nombre de fois que nous faisons le test, soit \(0,9 \times 0,9 \times 0,9 \times 0,9 \times 0,9 \times 0,9 = 0,9^6 = 0,53\). Tous les autres cas ayant au moins un test faux, nous constatons que notre analyse globale sera incorrecte \(1 - 0,53 = 47\%\) du temps50. Notre analyse sera incorrecte une fois sur deux environ.

De manière générale, le nombre de combinaisons deux à deux possibles dans un set de n groupes distincts sera calculé à l’aide du coefficient binomial que nous avions déjà rencontré avec la distribution du même nom, ici avec \(j\) valant deux.

\[C^j_n = \frac{n!}{j!(n-j)!}\]

Toujours avec notre approche naïve du risque d’erreur individuel pour un test \(r\) de 10%, le risque de se tromper au moins une fois est alors :

\[1 - (1 - r)^{C^2_n}\]

Voici ce que cela donne comme risque de se tromper dans au moins un des tests en fonction du nombre de groupes à comparer  :

Groupes comparés 2 à 2 2 3 4 6 8 10
Risque individuel = 10% 10% 27% 47% 79% 95% 99%

Clairement, on oublie cette façon de faire ! Prendre le risque de se tromper 99 fois sur 100 en comparant 10 groupes différents n’est pas du tout intéressante comme perspective.

Nous allons donc travailler différemment… Ci-après nous verrons qu’une simplification des hypothèses et l’approche par décomposition de la variance est une option bien plus intéressante (ANalysis Of VAriance ou ANOVA). Ensuite, nous reviendrons vers ces comparaisons multiples deux à deux, mais en prenant des précautions pour éviter l’inflation du risque global de nous tromper.

  1. Attention ! vous savez bien que c’est plus compliqué que cela. D’une part, le risque de se tromper est probablement différent si on rejette \(H_0\) (\(\alpha\)) ou non (\(\beta\)), et ces risques sont encore à moduler en fonction de la probabilité a priori, un cas similaire au dépistage d’une maladie plus ou moins rare, rappelez-vous, au module 7.↩

  2. Dans R, vous pouvez utiliser choose(n, j) pour calculer le coefficient binomial. Donc votre calcul du risque de se tromper au moins une fois dans un ensemble de n tests dont le risque individuel est r sera 1 - (1 - r)^choose(n, 2).↩