7.7 Distribution log-Normale
La loi log-Normale est utilisée pour représenter la distribution d’une variable aléatoire qui résulte de la multiplication d’un grand nombre de petits effets indépendants entre eux. C’est le cas en biologie et en chimie, par exemple, la taille d’un animal, la concentration d’une molécule en solution, la température d’un matériau, etc. Ces variables sont définies uniquement pour des valeurs nulles ou positives. Une taille et une concentration négatives ne sont pas possibles. De même pour une température en dessous du zéro absolu (attention, dans ce cas, la température doit être mesurée en Kelvin).
7.7.1 Transformée log
La distribution log-Normale devient Normale lorsque nous transformons la variable en son logarithme. Donc, si :
\[X \sim log{\text -}N(0, 0.5)\]
alors :
\[log(X) \sim N(0, 0.5)\]
Par facilité, on défini ses deux paramètres de manière relative à la moyenne \(\mu\) et à l’écart type \(\sigma\) qu’a la distribution Normale obtenue après transformation logarithmique. Voici à quoi ressemble la densité de probabilité de cette distribution (Fig 7.11). C’est une distribution asymétrique qui démarre du quantile zéro et est asymptotique à droite en \(+\infty\).
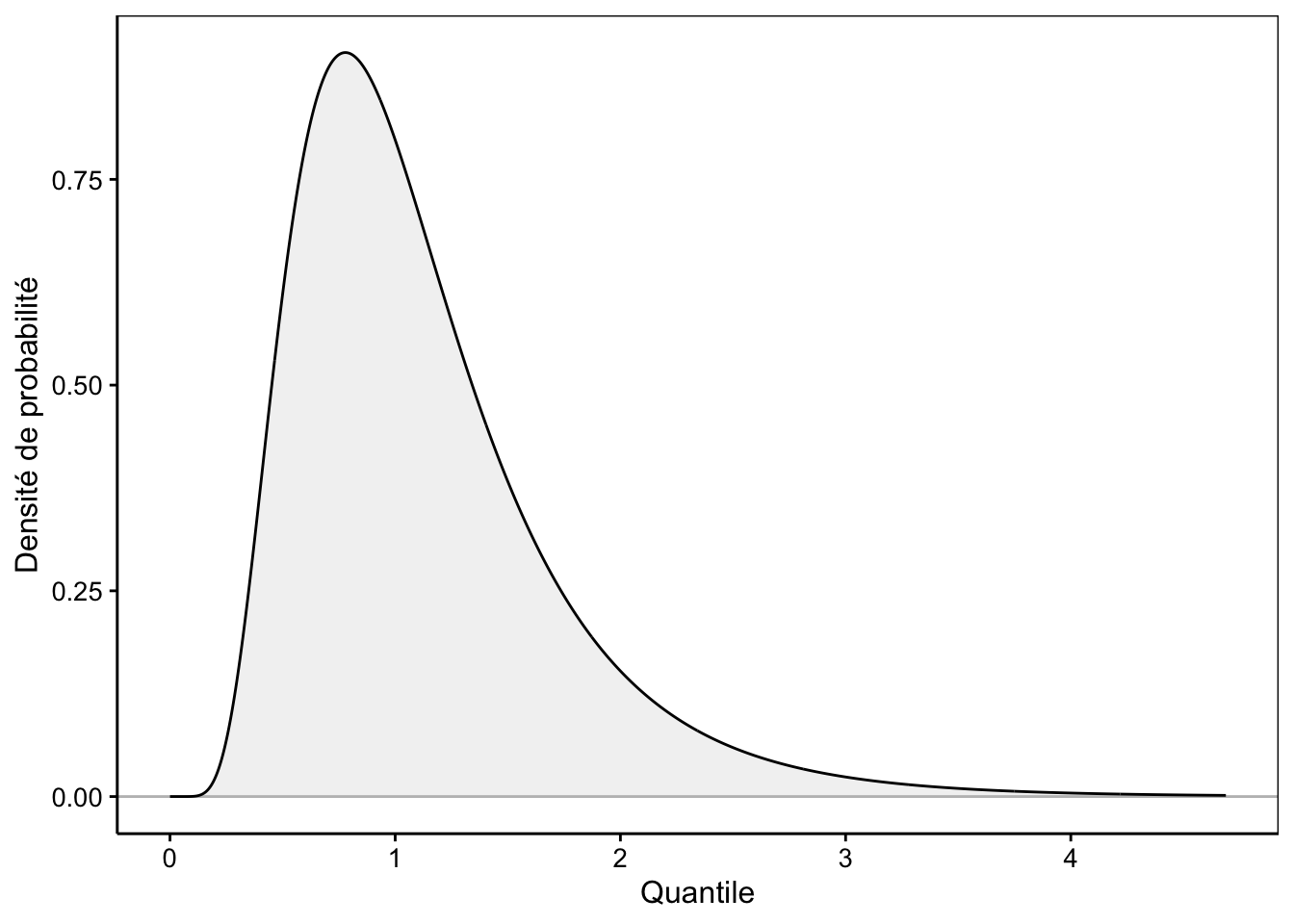
Figure 7.11: Un exemple de distribution log-Normale.
7.7.2 Snippets
Les fonctions relatives à la distribution log-Normale dans R sont <x>lnorm(). Le calcul de probabilités se fait à l’aide de plnorm(), les quantiles se déterminent à partir de qlnorm() et un échantillon pseudo-aléatoire se calcule en utilisant rlnorm(). Les snippets relatifs à la loi log-normale dans la SciViews Box sont accessibles à partir du menu (d)istributions: log-normal à partir de .il) :