10.2 ANOVA à un facteur

Au lieu de s’attaquer aux comparaisons deux à deux, nous pouvons aussi considérer une hypothèse unique que les moyennes de \(k\) populations (nos quatre groupes différents de crabes, par exemple) sont égales. L’hypothèse alternative sera qu’au moins une des moyennes diffère des autres. En formulation mathématique, cela donne :

\(H_0: \mu_1 = \mu_2 = ... = \mu_k\)
\(H_1: \exists(i, j) \mathrm{\ tel\ que\ } \mu_i \neq \mu_j\)

Notre hypothèse nulle est très restrictive, mais par contre, l’hypothèse alternative est très vague car nous ne savons pas où sont les différences à ce stade si nous rejetons \(H_0\), mais nous nous en occuperons plus tard.

Propriété d’additivité des parts de variance. La variance se calcule comme :

\[var_x = \frac{SCT}{ddl}\]

Avec \(SCT\), la somme des carrés totaux, soit \(\sum_{i = 1}^n (x_i - \bar{x})^2\), la somme des carrés des écarts à la moyenne générale. Les ddl sont les degrés de liberté déjà rencontrés à plusieurs reprises qui valent \(n - 1\) dans le cas de la variance d’un échantillon.

Cette variance peut être partitionnée. C’est-à-dire que, si la variance totale se mesure d’un point A à un point C, l’on peut mesurer la part de variance d’un point A à un point B, puis l’autre part d’un point B à un point C, et dans ce cas,

\[SCT = SC_{A-C} = SC_{A-B} + SC_{B-C}\]

Cette propriété, dite d’additivité des variances, permet de décomposer la variance totale à souhait tout en sachant que la somme des différentes composantes donne toujours la même valeur que la variance totale.

À vous de jouer !

10.2.1 Modèle de l’ANOVA

Mais qu’est-ce que cette propriété d’additivité des variances vient faire ici ? Nous souhaitons comparer des moyennes, non ? Effectivement, mais considérons le modèle mathématique suivant :

\[y_{ij} = \mu + \tau_j + \epsilon_i \mathrm{\ avec\ } \epsilon \sim N(0, \sigma)\]

Avec l’indice \(j = 1 .. k\) populations et l’indice \(i = 1 .. n\) observations du jeu de données. Chaque observation \(y_{ij}\) correspond à deux écarts successifs de la moyenne globale \(\mu\) : une constante “tau” par population \(\tau_j\) d’une part et un terme \(\epsilon_i\) que l’on appelle les résidus et qui est propre à chaque observation individuelle. C’est ce dernier terme qui représente la partie statistique du modèle avec une distribution normale centrée sur zéro et avec un écart type \(\sigma\) que nous admettrons constant et identique pour toutes les populations par construction.

Le graphique à la Fig. 10.3 représente une situation typique à trois sous-populations.

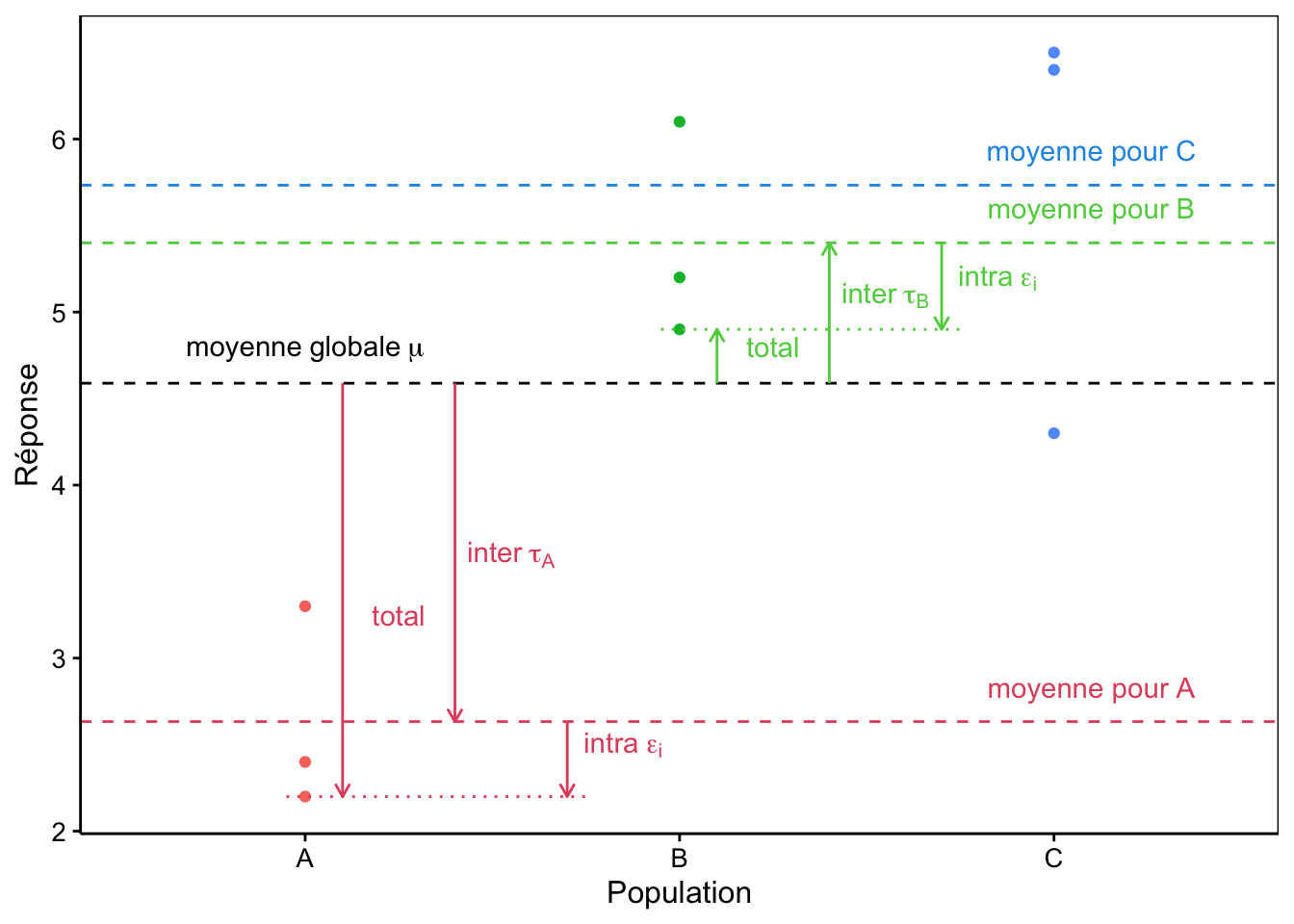
Figure 10.3: Décomposition de la variance dans un cas à trois populations A, B et C fictives.

Notons que ce modèle à trois termes représente bien la situation qui nous intéresse, mais aussi, qu’il décompose la variance totale (entre \(\mu\) et chaque point observé) en deux : ce que nous appellerons le terme inter représentant l’écart entre la moyenne globale \(\mu\) et la moyenne de la sous-population concernées (\(\tau_j\)) et le terme intra depuis cette moyenne de la sous-population jusqu’au point observé (\(\epsilon_i\)).

À vous de jouer !

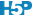
D’une part, nous nous trouvons dans une situation d’additivité de la variance si nous décidons de calculer ces “variance inter” et “variance intra”. D’autre part, sous \(H_0\) nous sommes sensés avoir toutes les moyennes égales à \(\mu\), et donc, tous les \(\tau_j = 0\). Donc, les valeurs non nulles de \(\tau_j\) ne doivent qu’être dus au hasard de l’échantillonnage et être par conséquent largement inférieurs à la variabilité entre les individus, ou variance intra \(\epsilon_i\). La Fig. 10.4 représente deux cas avec à gauche une situation où \(H_0\) est plausible, et à droite une situation où elle est très peu plausible. Notez qu’à gauche la variation entre les observations (intra) est bien plus grande que l’écart entre les moyennes (inter), alors qu’à droite c’est l’inverse.

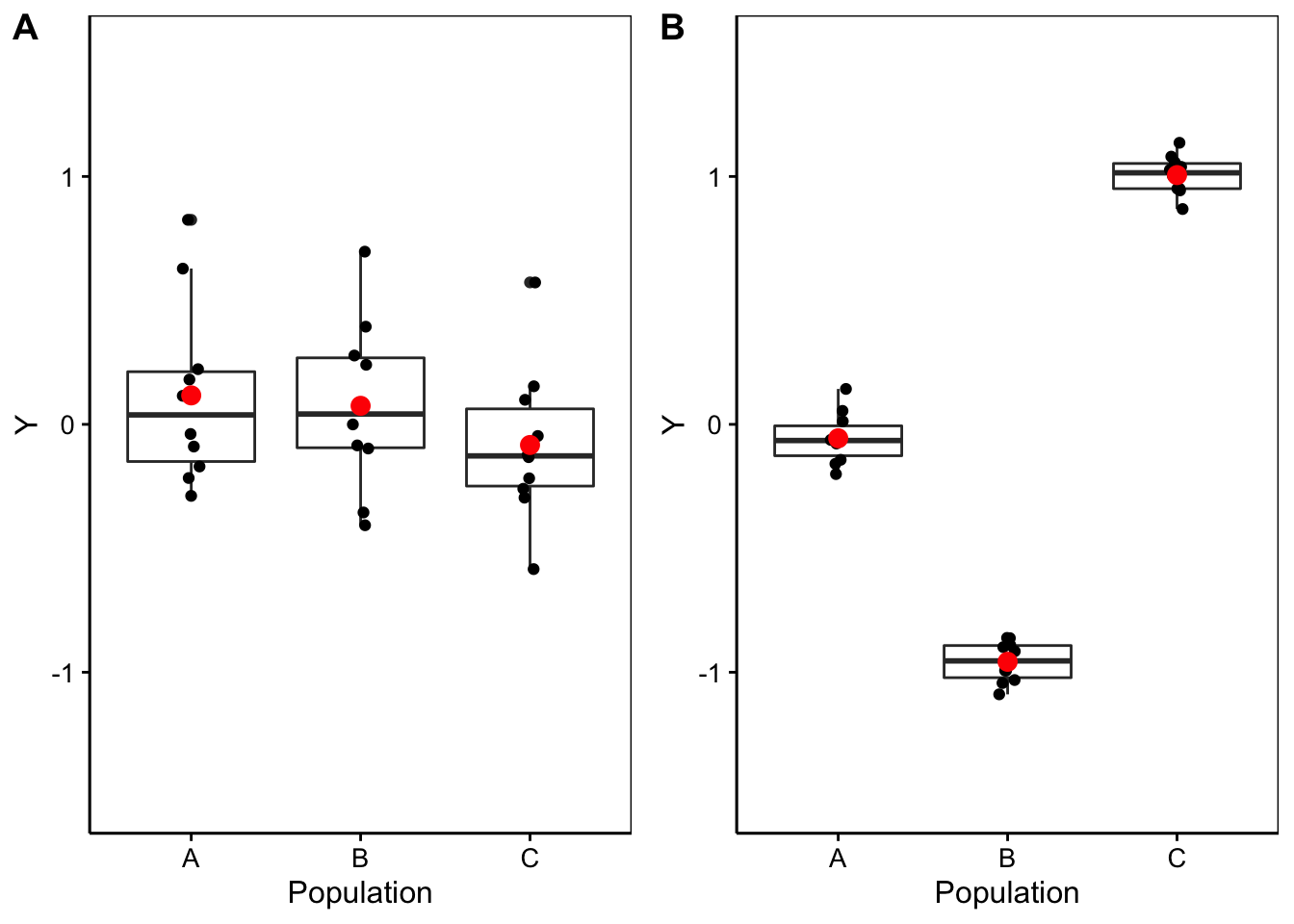
A. Cas fictif avec moyennes probablement égales entre populations (étalement des points bien plus large que l'écart entre les moyennes), B. cas où les moyennes sont probablement différentes (écart des moyennes "inter" bien plus grand que l'étalement des points en "intra"-population).

Figure 10.4: A. Cas fictif avec moyennes probablement égales entre populations (étalement des points bien plus large que l’écart entre les moyennes), B. cas où les moyennes sont probablement différentes (écart des moyennes “inter” bien plus grand que l’étalement des points en “intra”-population).

Intuitivement, une comparaison de “inter” et “intra” permet de différencier la situation de gauche de celle de droite dans la Fig. 10.4. Si cette comparaison est faite sous forme d’un ratio “inter”/“intra”, alors ce ratio sera faible et tendra vers zéro sous \(H_0\) (cas A), alors qu’il sera d’autant plus élevé que \(H_0\) devient de moins en moins plausible (cas B).

Calcul de l’ANOVA

Calcul des sommes des carrés (inter- et intragroupes). Considérant :

i = indice des observations au sein du jeu de données de 1 à n,
j = facteurs (sous-populations de 1 à k),
\(\bar{y}\) = moyenne générale de l’échantillon,
\(\bar{y_j}\) = moyenne de la j^ème population.

La somme des carrés inter \(SC_{inter}\) et la somme des carrés intra \(SC_{intra}\) se calculent comme suit :

\[ \begin{aligned} SC_{inter} = \sum_{i=1}^n{(\bar{y_j} - \bar{y})^2} && SC_{intra} = \sum_{i=1}^n{(y_{ij} - \bar{y_j})^2} \end{aligned} \]

A ces sommes des carrés, nous pouvons associer les degrés de liberté suivants :

k – 1 pour l’intergroupe
n – k pour l’intragroupe

Sachant que les parts de variances sont les \(\frac{SC}{ddl}\) et sont appelés “carrés moyens”, nous construisons ce qu’on appelle le tableau de l’ANOVA de la façon suivante :

Type	Ddl	Somme carrés	Carré moyen (CM)	Statistique F_obs	P (>F)
Inter (facteur)	k - 1	SC_inter	SC_inter/ddl_inter	CM_inter/CM_intra	…
Intra (résidus)	n - k	SC_intra	SC_intra/ddl_intra

La statistique F_obs est le rapport des carrés moyens inter/intra. Elle représente donc le ratio que nous avons évoqué plus haut comme moyen de quantifier l’écart par rapport à \(H_0\). Le test consiste à calculer la valeur P associée à cette statistique. Pour cela, il nous faut une distribution statistique théorique de F sous \(H_0\). C’est un biologiste - statisticien célèbre nommé Ronald Aylmer Fisher qui l’a calculée. C’est la distribution F de Fisher.

À vous de jouer !

10.2.2 Distribution F

La distribution F est une distribution asymétrique n’admettant que des valeurs nulles ou positives, d’une allure assez similaire à la distribution du \(\chi^2\) que nous avons étudiée au module 8. Elle est appelée loi de Fisher, ou encore, loi de Fisher-Snedecor. Elle a une asymptote horizontale à \(+\infty\). La distribution F admet deux paramètres, respectivement les degrés de liberté au numérateur (inter) et au dénominateur (intra). La Fig. 10.5 représente la densité de probabilité d’une loi F typique⁴⁸.

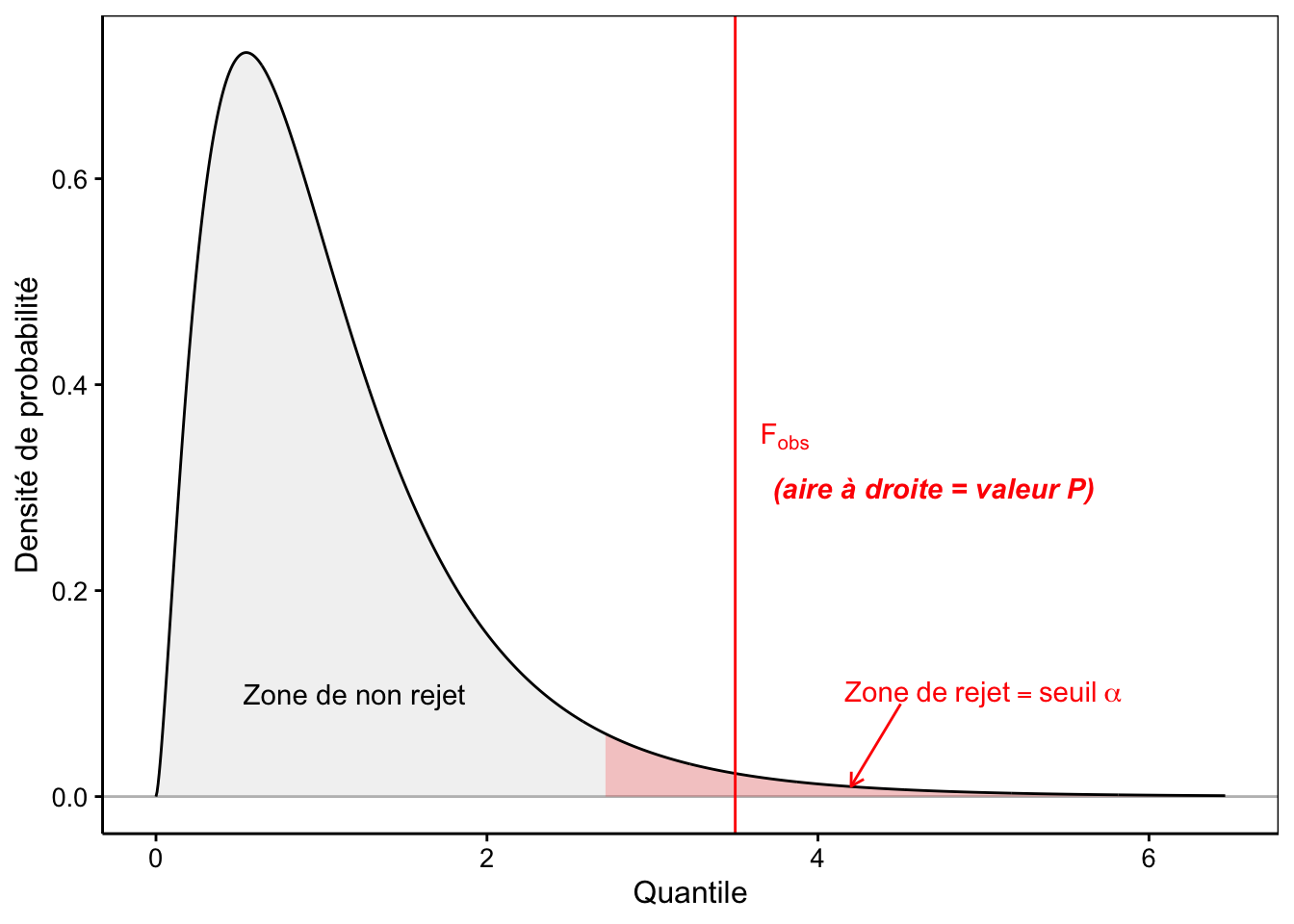
Allure typique de la densité de probabilité de la distribution F (ici ddl inter = 5 et ddl intra = 20). Plus *F~obs* est grand, plus l'hypothèse nulle est suspecte. La zone de rejet est donc positionnée à droite (en rouge).

Figure 10.5: Allure typique de la densité de probabilité de la distribution F (ici ddl inter = 5 et ddl intra = 20). Plus F~obs est grand, plus l’hypothèse nulle est suspecte. La zone de rejet est donc positionnée à droite (en rouge).

Nous commençons à avoir l’habitude maintenant. La valeur P est calculée comme l’aire à droite du quantile correspondant à F_obs. Enfin, nous rejetterons \(H_0\) seulement si la valeur P est inférieure au seuil \(\alpha\) qui a été choisi préalablement au test. Ceci revient à constater que, graphiquement, F_obs vient se positionner dans la zone de rejet en rouge comme sur la Fig. 10.5.

Conditions d’application

échantillon représentatif (par exemple, aléatoire),
observations indépendantes,
variable dite réponse quantitative,
une variable dite explicative qualitative à trois niveaux ou plus,
distribution normale des résidus \(\epsilon_i\),
homoscédasticité (même variance intragroupes, “homoscedasticity” en anglais, opposé à hétéroscédasticité = variance différente entre les groupes).

Les deux dernières conditions d’applications doivent être vérifiées. La normalité des résidus doit être rencontrée aussi bien que possible. Un graphique quantile-quantile des résidus permet de se faire une idée, comme sur la Fig. 10.6. Néanmoins, le test étant relativement robuste à des petites variations par rapport à la distribution normale, surtout si ces variations sont symétriques, nous ne seront pas excessivement stricts ici.

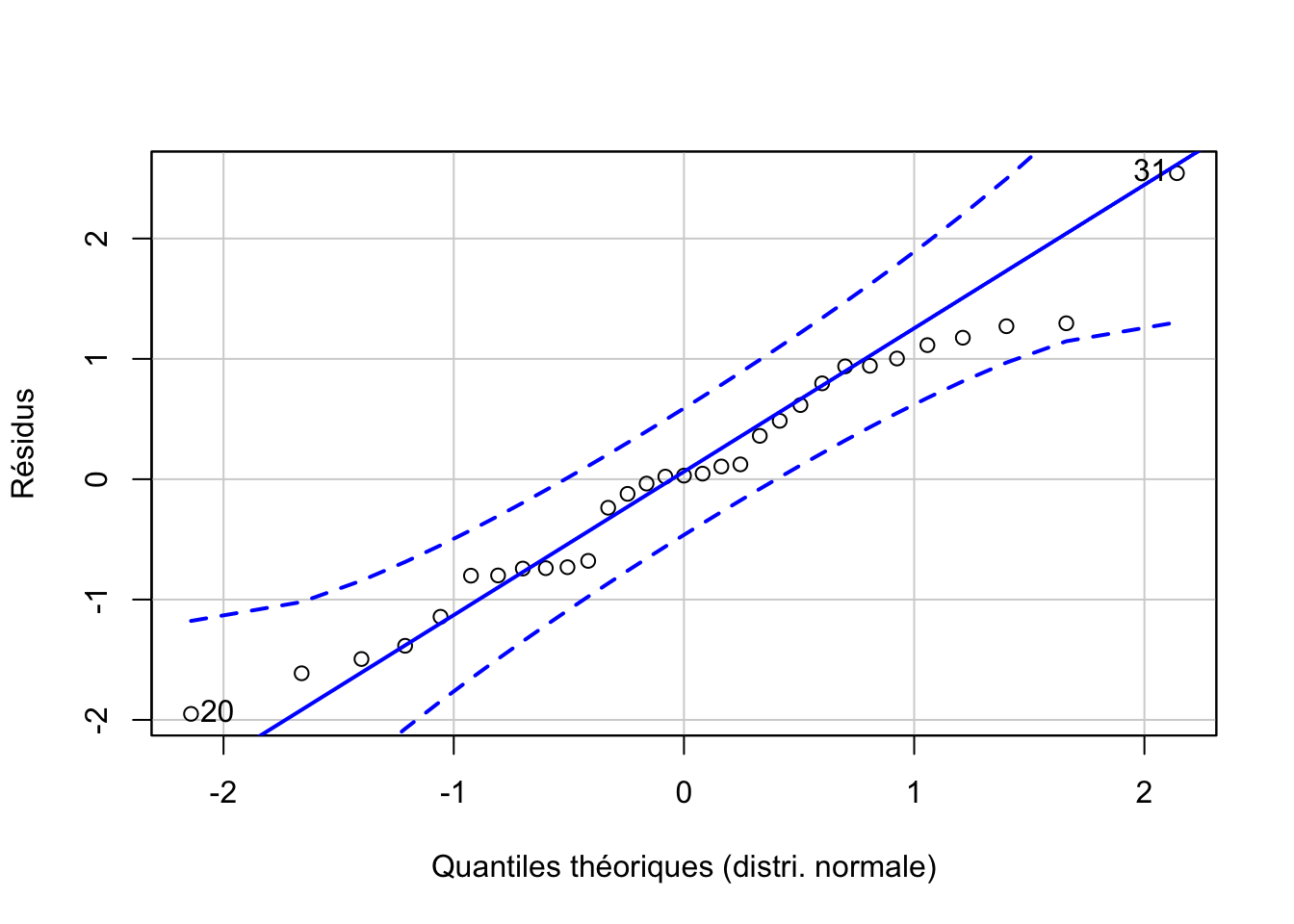
Figure 10.6: Graphique quantile-quantile appliqué aux résidus d’une ANOVA pour déterminer si leur distribution se rapproche d’un loi normale.

La condition d’homoscédasticité est plus sensible. Elle mérite donc d’être vérifiée systématiquement et précisément. Différents tests d’hypothèse existent pour le vérifier, comme le test de Batlett, le test de Levene, etc. Nous vous proposons ici d’utiliser le test de Batlett. Ses hypothèses sont :

\(H_0: var_1 = var_2 = ... = var_k\) (homoscédasticité)
\(H_1: \exists(i, j) \mathrm{\ tel\ que\ } var_i \neq var_j\) (hétéroscédasticité)

Si la valeur P est inférieure au seuil \(\alpha\) fixé au préalable, nous devrons rechercher une transformation des variables qui stabilisera la variance. La première transformation à essayer en biologie et la transformation logarithmique surtout si les valeurs négatives de la variable réponse ne sont pas possibles, signe d’une distribution qui peut être plutôt de type log-normale pour cette variable. Si aucune transformation ne stabilise la variance, nous devrons nous rabattre vers un test non paramétrique équivalent, le test de Kruskal-Wallis que nous aborderons plus loin dans ce module.

La SciViews Box propose des snippets pour accéder à ces différentes analyses. Dans le menu hypothesis tests: variances ou .hv nous trouvons trois tests dont celui de Bartlett. Dans le menu hypothesis tests: means ou .hm se trouvent les templates pour l’ANOVA, ainsi que les graphiques d’analyse des résidus dont le graphique quantile-quantile.

À vous de jouer !

Résolution de notre exemple

Nous commençons par déterminer si nous avons homoscédasticité. Considérons un seuil \(\alpha\) de 5% pour tous nos tests. Ensuite :

bartlett.test(data = crabs2, aspect ~ group)

# 
#   Bartlett test of homogeneity of variances
# 
# data:  aspect by group
# Bartlett's K-squared = 24.532, df = 3, p-value = 1.935e-05

Nous rejetons \(H_0\). Il n’y a pas homoscédasticité. Calculons par exemple le logarithme népérien de aspect et réessayons :

crabs2 %>.%
  mutate(., log_aspect = ln(aspect)) ->
  crabs2
bartlett.test(data = crabs2, log_aspect ~ group)

# 
#   Bartlett test of homogeneity of variances
# 
# data:  log_aspect by group
# Bartlett's K-squared = 37.891, df = 3, p-value = 2.981e-08

Ici cela ne fonctionne pas. Cela fait pire qu’avant. La transformation inverse (exp()) peut être essayée mais ne stabilise pas suffisamment la variance. Après divers essais, il s’avère qu’une transformation puissance cinq stabilise bien la variance.

crabs2 %>.%
  mutate(., aspect5 = aspect^5) ->
  crabs2
bartlett.test(data = crabs2, aspect5 ~ group)

# 
#   Bartlett test of homogeneity of variances
# 
# data:  aspect5 by group
# Bartlett's K-squared = 1.7948, df = 3, p-value = 0.6161

La Fig. 10.7 montre la distribution dans les différents groupes de la variable transformée.

chart(data = crabs2, aspect5 ~ group) +
  geom_violin() +
  geom_jitter(width = 0.05, alpha = 0.5) +
  geom_point(data = group_by(crabs2, group) %>.%
    summarise(., means = mean(aspect5, na.rm = TRUE)),
    f_aes(means ~ group), size = 3, col = "red") +
  ylab("(ratio largeur arrière/max)^5")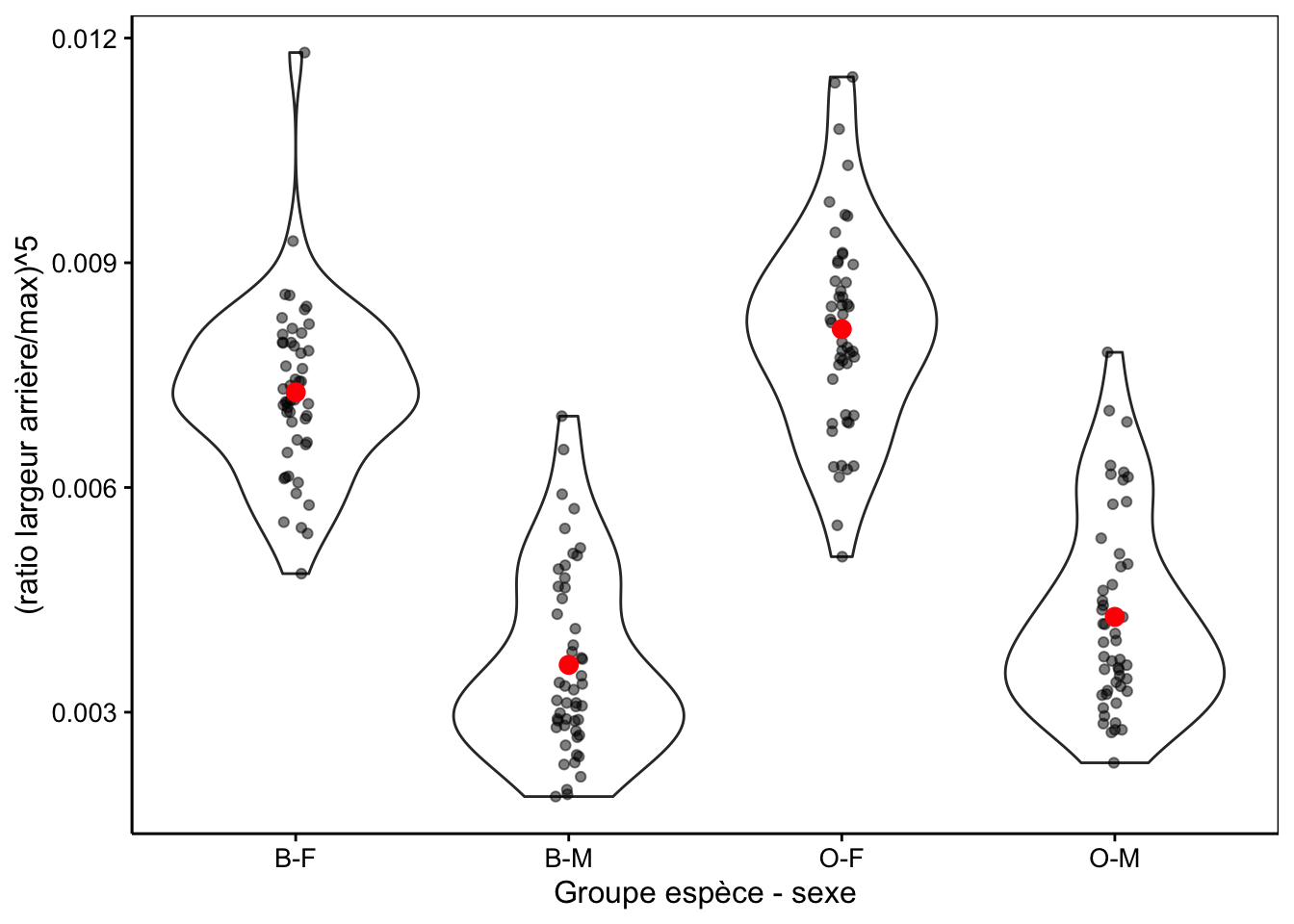

Figure 10.7: Transformation puissance cinq du ratio largeur arrière/largeur max en fonction du groupe de crabes L. variegatus.

Nous poursuivons sur une description des données utile pour l’ANOVA⁴⁹ :

crabs2 %>.%
  group_by(., group) %>.%
  summarise(.,
    mean  = mean(aspect5),
    sd    = sd(aspect5),
    count = sum(!is.na(aspect5)))

# # A tibble: 4 x 4
#   group    mean      sd count
#   <fct>   <dbl>   <dbl> <int>
# 1 B-F   0.00727 0.00115    50
# 2 B-M   0.00363 0.00124    50
# 3 O-F   0.00811 0.00138    50
# 4 O-M   0.00427 0.00130    50

Ensuite l’ANOVA proprement dite :

anova(anova. <- lm(data = crabs2, aspect5 ~ group))

# Analysis of Variance Table
# 
# Response: aspect5
#            Df     Sum Sq    Mean Sq F value    Pr(>F)    
# group       3 0.00072741 2.4247e-04  150.53 < 2.2e-16 ***
# Residuals 196 0.00031572 1.6110e-06                      
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nous retrouvons ici le tableau de l’ANOVA. La valeur P est très faible et inférieure à \(\alpha\). Nous rejetons \(H_0\). Nous pouvons dire que le ratio largeur arrière / max à la puissance cinq diffère significativement entre les groupes (ANOVA, F = 150, ddl = 3 & 196, valeur P << 10^-3).

Ce n’est qu’une fois l’ANOVA réalisée que nous pouvons calculer et visionner la distribution des résidus (Fig. 10.8). Cette distribution s’éloigne aux extrêmes de la distribution normale. Nous sommes dans un cas un peu limite. Soit nous considérons que l’écart est suffisamment léger pour ne pas trop influer sur l’ANOVA, soit nous devons passer à un test non paramétrique. Nous ferons les deux ici à des fins de comparaison.

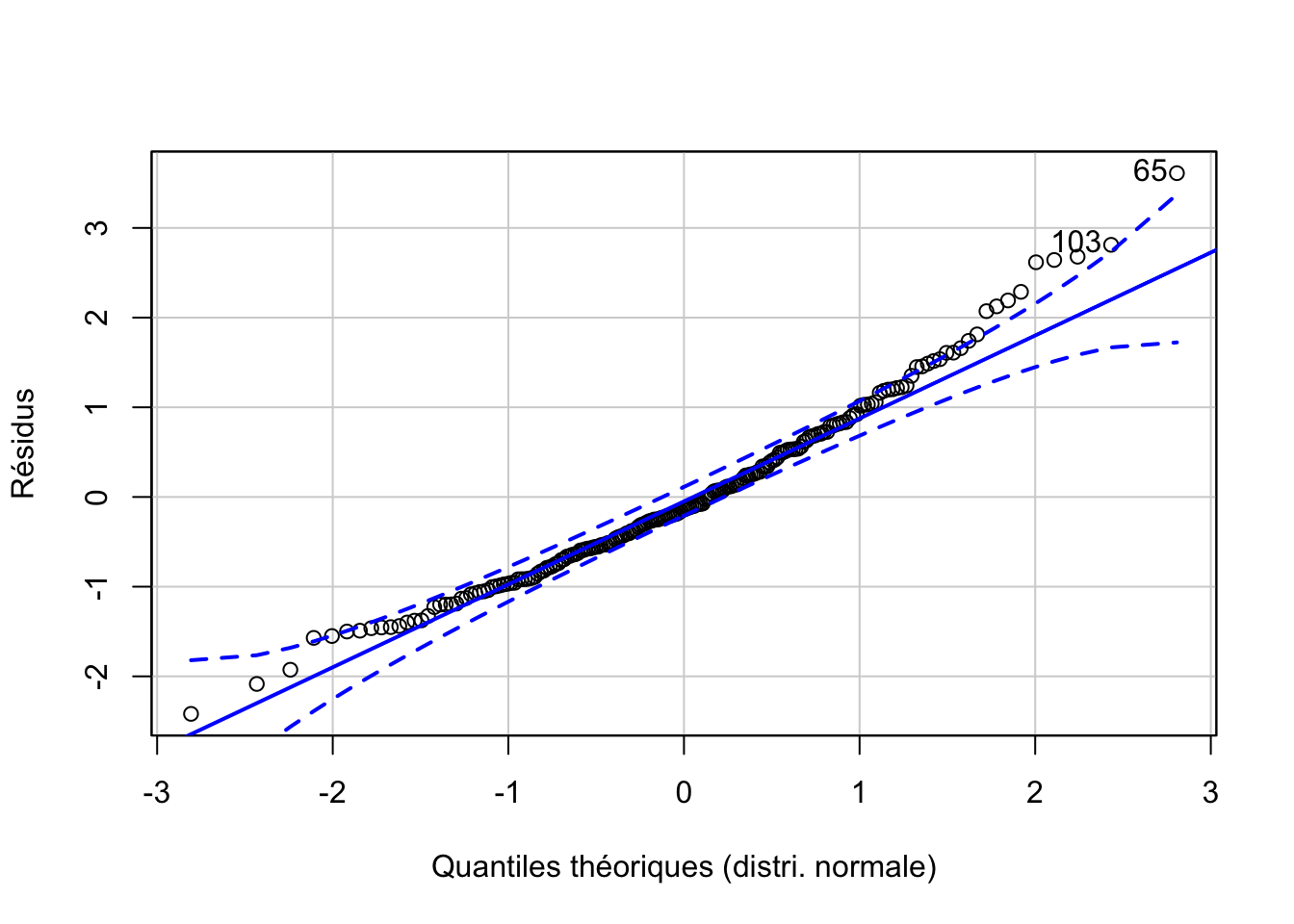
Figure 10.8: Graphique quantile-quantile des résidus pour l’analyse de aspect^5.

# [1]  65 103

Pour en savoir plus

L’ANOVA expliquée en trois minutes
Introduction to ANOVA (en anglais). Part I, part II, part III, part IV, and part V.
Explication de l’analyse de variance en détaillant le calcul par la Kahn academy. Partie I, partie II et partie III. Assez long : près de 3/4h en tout. Ne regardez que si vous n’avez pas compris ce que sont les sommes des carrés.