6.5 Test de corrélation

C’est bien beau de pouvoir quantifier une corrélation, mais à partir de quand est-elle significative au sens statistique du terme? En d’autres termes, nous voudrions déterminer si l’allongement du nuage de points peut être fortuit (par le biais de l’échantillonnage aléatoire) ou non. Il existe un test d’hypothèse qui répond à cette question. La section suivante présente traite de l’échantillonnage, du travail préliminaire ainsi que la définition d’un test d’hypothèse.

6.5.1 Échantillonnage

Nous avons déjà abordé cette question dans le chapitre 5. Si nous pouvions mesurer tous les individus d’une population à chaque fois, nous n’aurions pas besoin des statistiques. Mais ce n’est pratiquement jamais possible. Tout d’abord, le nombre d’individus est potentiellement très grand. Le travail nécessaire risque alors d’être démesuré. Afin de limiter les mesures à un nombre raisonnable de cas, nous effectuons un échantillonnage qui consiste à prélever un petit sous-ensemble de taille $N$ donné depuis la population de départ. Il existe différentes stratégies d’échantillonnage, que nous avons déjà abordées.

À vous de jouer !

Nous n’avons pas forcément accès à tous les individus d’une population. Dans ce cas, nous devons la limiter à un sous-ensemble raisonnable. Par exemple, il est impossible de mesurer toutes les souris. Par contre, nous pouvons décider d’étudier la ou les souches de souris disponibles dans l’animalerie, ou chez nos fournisseurs.

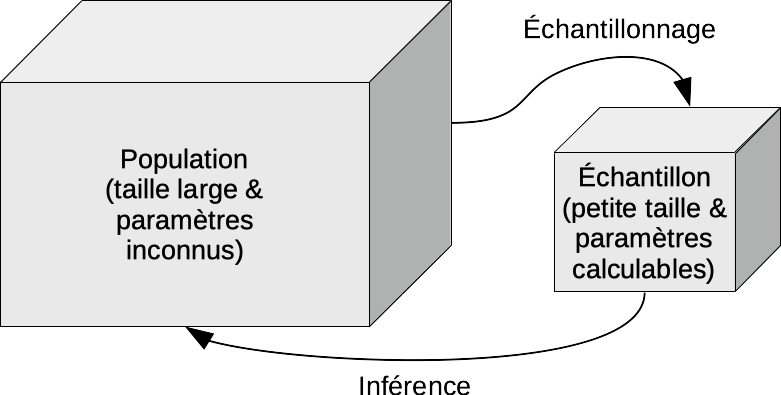
Quoi qu’il en soit, l’échantillon n’est qu’un petit sous-ensemble, si possible sélectionné par un mécanisme faisant intervenir le hasard. Donc, deux échantillons issus de la même population ont une très forte probabilité d’être différents l’un de l’autre. Il en va également de même des statistiques calculées sur ces échantillons, comme les effectifs observés pour chaque niveau de variables qualitatives ou les valeurs moyennes pour les variables quantitatives, par exemple. Cette variabilité d’un échantillon à l’autre ne nous intéresse pas, car elle n’apporte pas d’information sur la population elle-même. Ce qui nous intéresse, c’est d’estimer au mieux les grandeurs (effectifs par niveaux, moyennes, etc.) qui caractérisent la population toute entière.

L’estimation de paramètres d’une population par le biais de calculs sur un échantillon représentatif issu de cette population s’appelle l’inférence statistique. Rappelez-vous le schéma qui relie population et échantillon via l’échantillonnage d’une part, et l’inférence d’autre part.

À vous de jouer !

Travail préliminaire

Avant de vous lancer dans l’inférence statistique, assurez-vous d’avoir effectué soigneusement les trois étapes suivantes :

Vous comprenez bien la question posée, en termes biologiques. Vous connaissez ou vous vous êtes documenté sur l’état de l’art en la matière (bibliographie). Que sait-on déjà du phénomène étudié ? Quels sont les aspects encore inconnus ou à l’état de simples hypothèses ?
Vous avez vérifié que la façon dont les mesures ont été prises permettra effectivement de répondre à la question posée. En particulier, vous avez vérifié que l’échantillonnage a été réalisé dans les règles pour qu’il soit représentatif de la population étudiée. En outre, vous cernez clairement quelle est la population effectivement étudiée. C’est important pour éviter plus tard de surgénéraliser les résultats obtenus (les attribuer à une population plus large que celle effectivement étudiée).
Vous avez effectué une analyse exploratoire des données. Vous avez représenté les données à l’aide de graphiques appropriés et vous avez interprété ces graphiques afin de comprendre ce que le jeu de données contient. Vous avez également résumé les données sous forme de tableaux synthétiques et vous avez, si nécessaire, remanié et nettoyé vos données.

6.5.2 Test d’hypothèse

Le test d’hypothèse ou test statistique est l’outil le plus simple pour répondre à une question par l’inférence statistique. Il s’agit ici de réduire la question à sa plus simple expression en la réduisant à deux hypothèses contradictoires (en gros, la réponse à la question est soit “oui”, soit “non” et rien d’autre).

L’hypothèse nulle, notée $H_0$ est l’affirmation de base ou de référence que l’on cherchera à réfuter,
L’hypothèse alternative, notée $H_1$ ou $H_a$ représente une autre affirmation qui doit nécessairement être vraie si $H_0$ est fausse.

Les deux hypothèses ne sont pas symétriques. Notre intention est de rejeter $H_0$. Dans ce cas, nous pourrons considérer que $H_1$ est vraie avec un certain degré de certitude que nous pourrons également quantifier. Si nous n’y arrivons pas, nous dirons que nous ne pouvons pas rejeter $H_0$, mais nous ne pourrons jamais dire que nous l’acceptons, car dans ce cas, deux explications resteront possibles : (1) $H_0$ est effectivement vraie, ou (2) $H_0$ est fausse mais nous n’avons pas assez de données à disposition pour le démontrer avec le niveau de certitude recherché.

À vous de jouer !

Revenons à notre réflexion qui a initié la réalisation d’un test d’hypothèse. À partir de quand une corrélation entre deux variables est-elle significative ? Il existe un test d’hypothèse qui répond à cette question, avec une version pour chacun des trois coefficients de corrélation : r de Pearson, $\rho$ de Spearman et $\tau$ de Kendall. Pour r de Pearson, nous aurons les hypothèses suivantes :

$H_0\ :\ r = 0$
$H_1\ :\ r \neq 0$

Il existe aussi des variantes unilatérales à gauche ($H_1\ :\ r < 0$, dans r less) ou à droite ($H_1\ :\ r > 0$, dans r greater) dans le cas où nous aurions des indications que l’association ne peut qu’être de type proportionnalité inverse ou directe, respectivement.

Prenons l’exemple de r pour les deux variables les plus corrélées dans trees : diameter et volume. Notez la forme particulière de la formule à utiliser. Comme les deux variables sont sur le même pied d’égalité, il n’y a pas de raison d’en placer une à gauche du signe ~ dans la formule. On l’écrit alors ~ var1 + var2.

cor.test(data = trees, ~ diameter + volume, alternative = "greater")

# 
#   Pearson's product-moment correlation
# 
# data:  diameter and volume
# t = 20.44, df = 29, p-value < 2.2e-16
# alternative hypothesis: true correlation is greater than 0
# 95 percent confidence interval:
#  0.9394172 1.0000000
# sample estimates:
#       cor 
# 0.9670023

L’exécution de ce code nous donne un rapport avec :

Un titre qui précise le test d’hypothèse effectué (test de corrélation de Pearson avec des probabilités sous $H_0$)
Les variables employées pour ce test
L’hypothèse alternative du test
La dernière ligne donne la valeur précise de la corrélation entre les deux variables
Le résultat du test se trouve au niveau de la valeur de P à la troisième ligne. L’interprétation se fait en fonction de la valeur P. En fonction d’un seuil choisi avant de faire le test, et appelé seuil $\alpha$. La décision est prise comme suit :
- Si la valeur P est inférieure à $\alpha$, nous rejetons l’hypothèse $H_0$, considérée comme trop peu probable,
- Si la valeur P est supérieure ou égale à $\alpha$, nous ne rejetons pas $H_0$, et considérons que notre échantillon ne nous permet pas de considérer cette hypothèse nulle comme suffisamment improbable (soit elle est effectivement correcte, soit l’effectif $N$ de notre échantillon est insuffisant pour démontrer qu’elle ne l’est pas au seuil $\alpha$ choisi).

Souvent en biologie, on choisi $\alpha$ = 5%, mais dans les cas où nous souhaitons avoir plus de “certitude” dans notre réponse, nous pouvons aussi choisir un seuil plus restrictif de 1%, voire de 0,1%. Encore une fois, les explications sont détaillées ci-dessous.

Prenons la valeur courante en biologie afin d’intepréter ce test. Le test réalisé est un test unilatéral à droite avec alternative = "greater" puisque le volume de bois ne peut qu’augmenter avec le diamètre de l’arbre (relation inverse non crédible ici).

On peut utiliser la fonction tabularise() afin d’obtenir un tableau bien formaté pour un carnet de notes.

cor.test(data = trees, ~ diameter + volume, alternative = "greater") |> tabularise()

# Warning in set2(resolve(...)): The object is read-only and cannot be modified.
# If you have to modify it for a legitimate reason, call the method $lock(FALSE)
# on the object before $set(). Using $lock(FALSE) to modify the object will be
# enforced in future versions of knitr and this warning will become an error.

Test de corrélation de Pearson unilatéral à droite
Coefficent de Pearson r (IC:95%)	Valeur de tobs.	Ddl	Valeur sous H0	Valeur de p
1.0 (0.9-1.0)	20.4	29	0	4.55·10-19	***
0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Comme la valeur p est inférieure à $\alpha$, nous pouvons rejeter $H_0$ et conclure que le coefficient de corrélation entre le diamètre et le volume est significativement positif au seuil $\alpha$ de 5% (r = 0.967, ddl = 29, valeur p << 0.001).

On s’en doutait avec un coefficient aussi proche de 1. Mais qu’en est-il pour l’association entre le diamètre et la hauteur ?

cor.test(data = trees, ~ diameter + height, alternative = "greater") |> tabularise()

# Warning in set2(resolve(...)): The object is read-only and cannot be modified.
# If you have to modify it for a legitimate reason, call the method $lock(FALSE)
# on the object before $set(). Using $lock(FALSE) to modify the object will be
# enforced in future versions of knitr and this warning will become an error.

Test de corrélation de Pearson unilatéral à droite
Coefficent de Pearson r (IC:95%)	Valeur de tobs.	Ddl	Valeur sous H0	Valeur de p
0.5 (0.3-1.0)	3.27	29	0	0.0014	**
0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Elle est, elle aussi, significative au seuil $\alpha$ de 5%. La valeur p vaut ici un peu plus de 0,1%. Que donnerait un test de Spearman sur ces mêmes variables ?

cor.test(data = trees, ~ diameter + height,
  alternative = "greater", method = "spearman") |> tabularise()

# Warning in cor.test.default(x = mf[[1L]], y = mf[[2L]], ...): Cannot compute
# exact p-value with ties

# Warning in set2(resolve(...)): The object is read-only and cannot be modified.
# If you have to modify it for a legitimate reason, call the method $lock(FALSE)
# on the object before $set(). Using $lock(FALSE) to modify the object will be
# enforced in future versions of knitr and this warning will become an error.

Test de corrélation de Spearman unilatéral à droite
Coefficent de Spearman $\rho$	Valeur de Sobs.	Valeur sous H0	Valeur de p
0.441	2773	0	0.00653	**
0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Le test nous avertit qu’en présence d’ex aequo, le calcul n’est qu’approchant. Ici aussi, nous rejetons $H_0$. Enfin, pour comparaison (en pratique, on ne fait pas systématiquement tous les tests, mais on choisit celui qui est le plus adéquat), que donnerait un test de Kendall ?

cor.test(data = trees, ~ diameter + height,
  alternative = "greater", method = "kendall") |> tabularise()

# Warning in cor.test.default(x = mf[[1L]], y = mf[[2L]], ...): Cannot compute
# exact p-value with ties

# Warning in set2(resolve(...)): The object is read-only and cannot be modified.
# If you have to modify it for a legitimate reason, call the method $lock(FALSE)
# on the object before $set(). Using $lock(FALSE) to modify the object will be
# enforced in future versions of knitr and this warning will become an error.

Test de corrélation de Kendall unilatéral à droite
Coefficient de Kendall $\tau$	Valeur de Zobs.	Valeur sous H0	Valeur de p
0.317	2.46	0	0.007	**
0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Même remarque concernant les ex aequo et valeur p très similaire ici à celle du test de Spearman.

Nous venons de réaliser nos premiers tests d’hypothèses. Dans les prochains modules, nous approfondirons la compréhension des tests d’hypothèses.

À vous de jouer !

Effectuez maintenant les exercices du tutoriel A06Lc_correlation (Association de deux variables).

BioDataScience1::run("A06Lc_correlation")

Réalisez le travail A06Ia_correlation, partie I.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques I : inférence à l’UMONS à terminer avant le 2025-05-19 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie I.