7.4 Graphique quantile-quantile
Il n’est pas toujours facile de déterminer quelle est la loi de distribution qui correspond le mieux à la population étudiée. Par contre, une comparaison est possible entre une distribution observée (sur base d’un échantillon, donc, d’un jeu de données) et une distribution théorique (sur base d’une loi théorique). Nous pouvons calculer les quantiles d’un échantillon via une méthode similaire à celle que nous avons employée pour calculer les quartiles et tracer la boite de dispersion dans le module 3.
Un quantile divise des données quantitatives en deux sous-groupes de telle manière que le groupe contenant les observations plus petites que ce quantile représente un effectif équivalent à la fraction considérée. Donc, un quantile 10% correspondra à la valeur qui sépare le jeu de données en 10% des observations les plus petites et 90% des observations les plus grandes.
Ce quantile dit observé est comparable au quantile dit théorique que nous pouvons calculer sur base d’une probabilité équivalente à la fraction considérée. Prenons un exemple simple pour fixer les idées. Dans les données relatives au plancton, nous avons 50 œufs allongés mesurés. Nous nous demandons si leur taille mesurée ici par la surface (variable area) de la particule à l’image suit une distribution log-normale. Dans ce cas, il est plus facile de transformer les données en logarithme et de comparer les valeurs ainsi recalculées à une distribution normale.
read("zooplankton", package = "data.io") %>.%
sfilter(., class == "Egg_elongated") %>.%
smutate(., log_area = log10(area)) %>.%
sselect(., area, log_area) ->
eggs
summary(eggs)# area log_area
# Min. :0.4121 Min. :-0.3850
# 1st Qu.:0.4714 1st Qu.:-0.3266
# Median :0.4950 Median :-0.3054
# Mean :0.5100 Mean :-0.2950
# 3rd Qu.:0.5347 3rd Qu.:-0.2719
# Max. :0.6718 Max. :-0.1728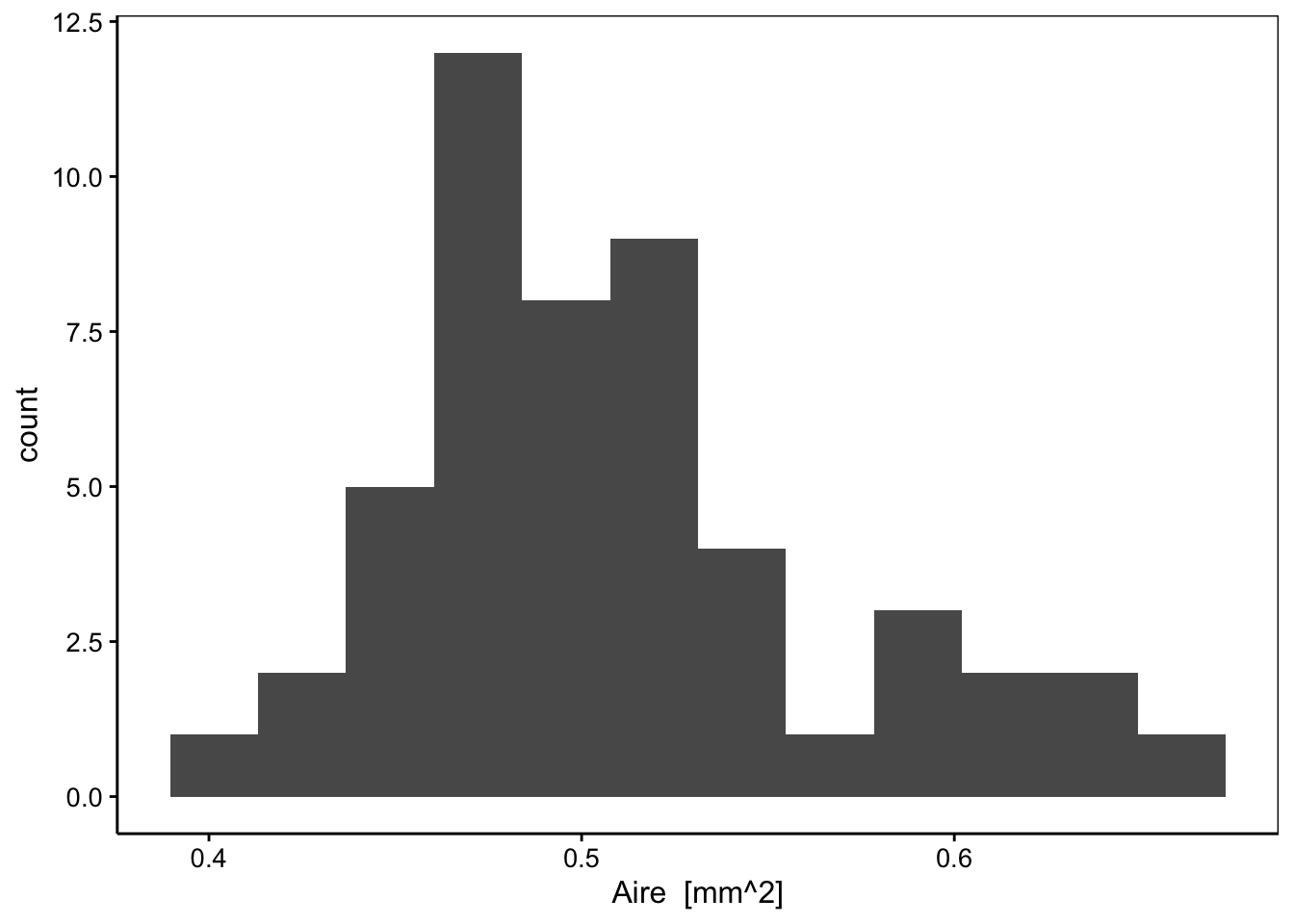
Sur base de l’histogramme, nous voyons bien que la distribution est soit unimodale et asymétrique, soit bimodale. L’histogramme des données transformées log devrait être plus symétrique si les données originelles suivent bien une distribution log-normale unimodale.
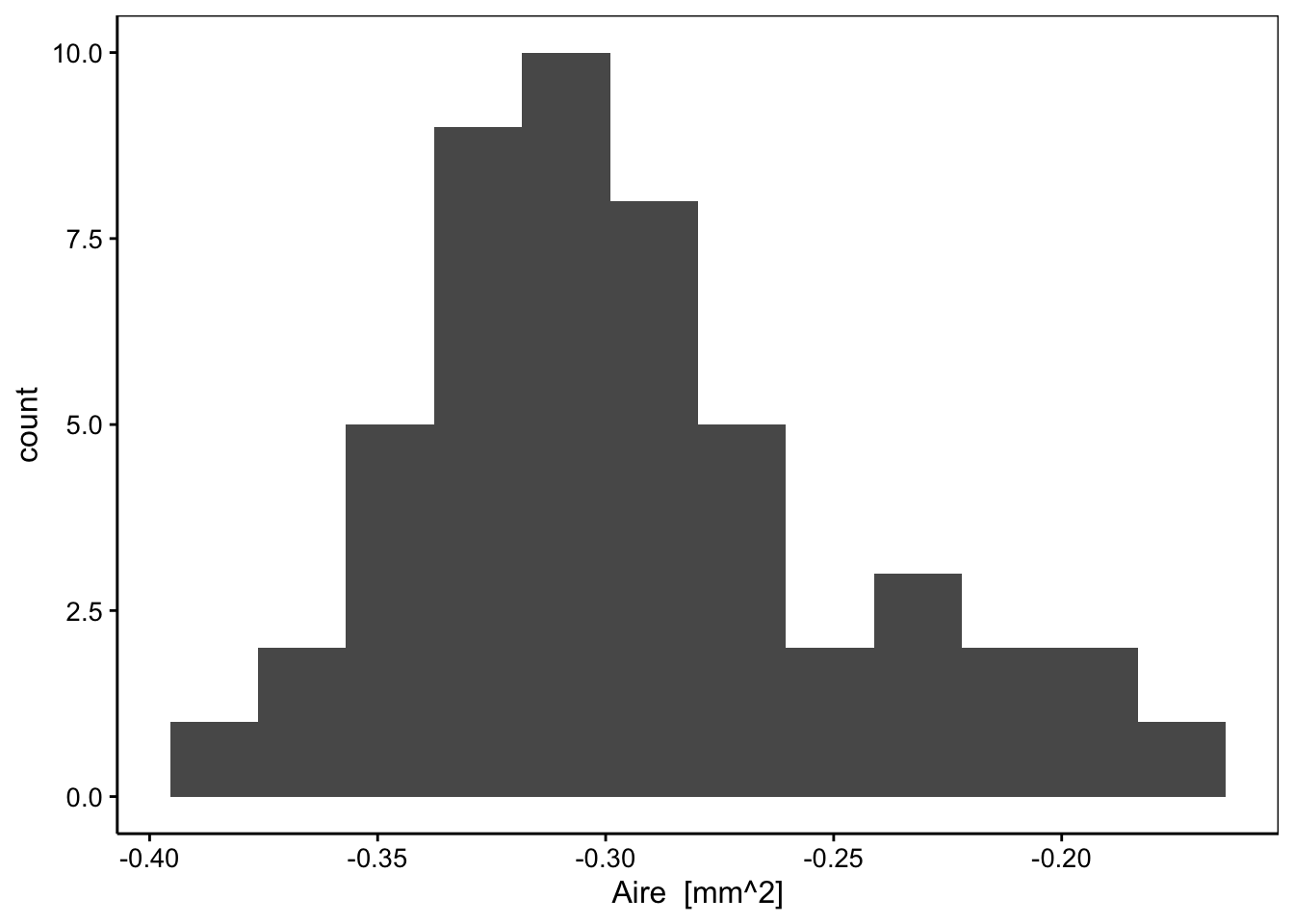
C’est légèrement mieux, mais la distribution ne parait pas parfaitement symétrique, voire peut-être encore bimodale (pas flagrant toutefois). L’histogramme est un bon outil pour visualiser globalement une distribution, mais le graphique quantile-quantile offre une représentation plus précise pour comparer deux distributions. Comme nous avons 50 observations à disposition, nous pouvons calculer les quantiles tous les 2% à l’aide de la fonction quantile(). De même, nous pouvons utiliser qnorm() pour calculer les quantiles théoriques selon une distribution normale réduite. Cela donne :
# [1] 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 0.20 0.22 0.24 0.26 0.28 0.30
# [16] 0.32 0.34 0.36 0.38 0.40 0.42 0.44 0.46 0.48 0.50 0.52 0.54 0.56 0.58 0.60
# [31] 0.62 0.64 0.66 0.68 0.70 0.72 0.74 0.76 0.78 0.80 0.82 0.84 0.86 0.88 0.90
# [46] 0.92 0.94 0.96 0.98# Quantiles observés dans l'échantillon
q_obs <- quantile(eggs$log_area, probs = probas)
# quantiles theoriques selon la distribution normale réduite
q_theo <- qnorm(probas, mean = 0, sd = 1)
qq <- dtx(q_obs = q_obs, q_theo = q_theo)
qq# q_obs q_theo
# <num> <num>
# 1: -0.3728814 -2.05374891
# 2: -0.3670666 -1.75068607
# 3: -0.3506297 -1.55477359
# 4: -0.3479900 -1.40507156
# 5: -0.3461128 -1.28155157
# 6: -0.3433854 -1.17498679
# 7: -0.3427930 -1.08031934
# 8: -0.3358312 -0.99445788
# 9: -0.3332840 -0.91536509
# 10: -0.3318941 -0.84162123
# 11: -0.3288629 -0.77219321
# 12: -0.3271749 -0.70630256
# 13: -0.3259333 -0.64334541
# 14: -0.3250031 -0.58284151
# 15: -0.3242584 -0.52440051
# 16: -0.3202637 -0.46769880
# 17: -0.3183681 -0.41246313
# 18: -0.3180753 -0.35845879
# 19: -0.3166605 -0.30548079
# 20: -0.3149042 -0.25334710
# 21: -0.3140506 -0.20189348
# 22: -0.3112096 -0.15096922
# 23: -0.3088567 -0.10043372
# 24: -0.3070501 -0.05015358
# 25: -0.3054387 0.00000000
# 26: -0.3028376 0.05015358
# 27: -0.2977052 0.10043372
# 28: -0.2930208 0.15096922
# 29: -0.2900899 0.20189348
# 30: -0.2882954 0.25334710
# 31: -0.2863555 0.30548079
# 32: -0.2849369 0.35845879
# 33: -0.2839382 0.41246313
# 34: -0.2834226 0.46769880
# 35: -0.2810512 0.52440051
# 36: -0.2767086 0.58284151
# 37: -0.2750341 0.64334541
# 38: -0.2697260 0.70630256
# 39: -0.2672149 0.77219321
# 40: -0.2632906 0.84162123
# 41: -0.2569700 0.91536509
# 42: -0.2460171 0.99445788
# 43: -0.2332825 1.08031934
# 44: -0.2318994 1.17498679
# 45: -0.2272695 1.28155157
# 46: -0.2135894 1.40507156
# 47: -0.2118190 1.55477359
# 48: -0.1989886 1.75068607
# 49: -0.1883088 2.05374891
# q_obs q_theoSi les deux distributions sont compatibles, nous devrions avoir une proportionnalité entre les quantiles théoriques et les quantiles observés. Cela devrait donc se marquer par un alignement des points sur un graphique des quantiles observés en fonction des quantiles théoriques (Fig. 7.5).
chart(data = qq, q_obs ~ q_theo) +
geom_point() +
labs(x = "Quantiles théoriques", y = "Quantiles observés")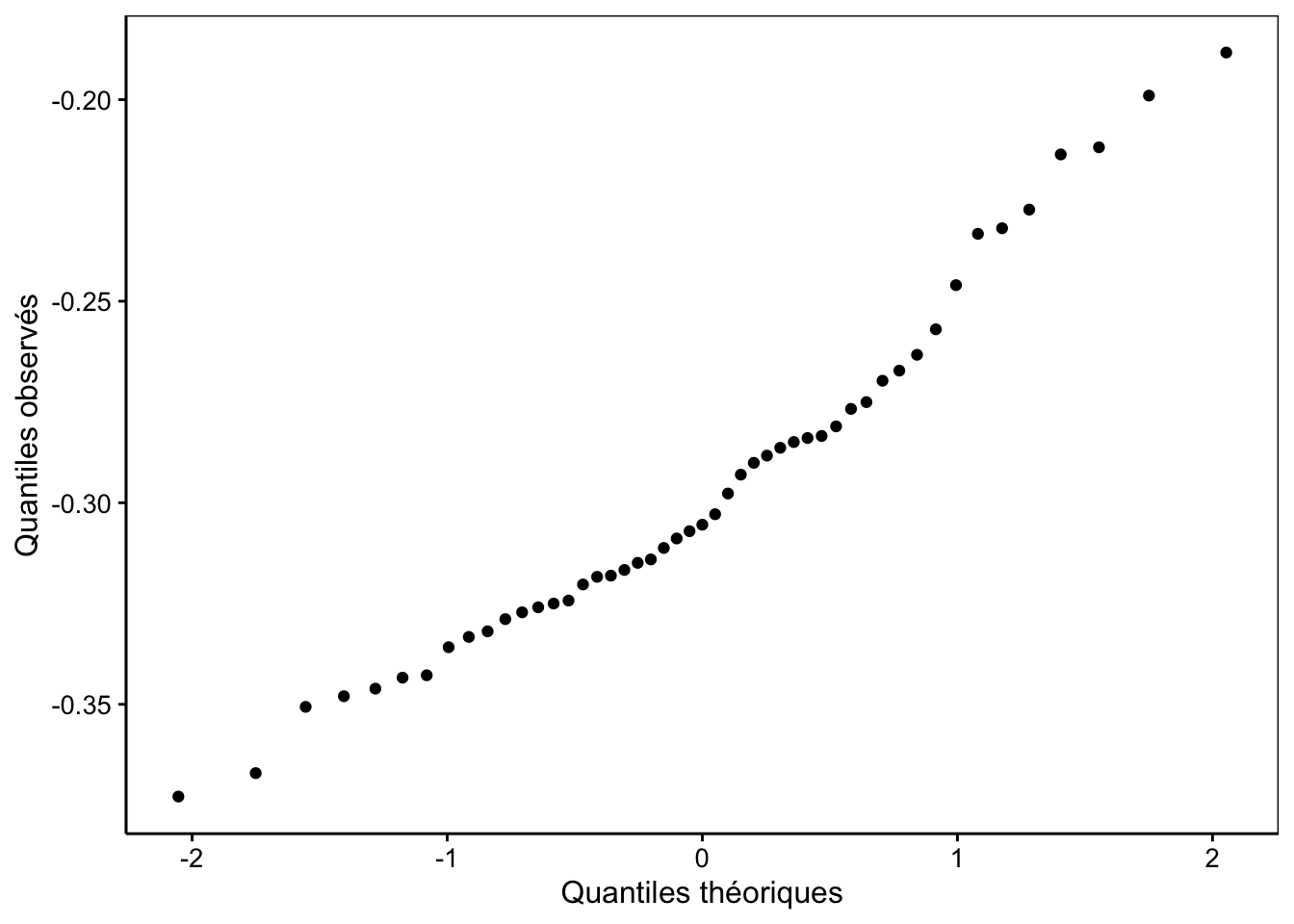
Figure 7.5: Graphique quantile-quantile construit à la main.
Cet alignement n’est pas flagrant. Le graphique proposé par la fonction car::qqPlot() (Fig. 7.6) est le même, mais il ajoute différents éléments qui aident à l’interprétation :
- Une droite (ligne continue bleue) selon laquelle les points devraient s’aligner en cas de concordance parfaite entre les deux distributions
- Une enveloppe de confiance (lignes pointillées bleues) qui tient compte de la variabilité aléatoire d’un échantillon à l’autre pour inclure une enveloppe de tolérance avec une fiabilité de 95%. Cela signifie que 95% des points doivent, en principe, se trouver à l’intérieur de l’enveloppe.
- Une individualisation des points les plus suspects éventuels, en indiquant le numéro de la ligne dans le jeu de donnée de chaque point suspect.
car::qqPlot(eggs[["log_area"]], distribution = "norm",
envelope = 0.95, col = "Black", ylab = "log(area [mm^2])")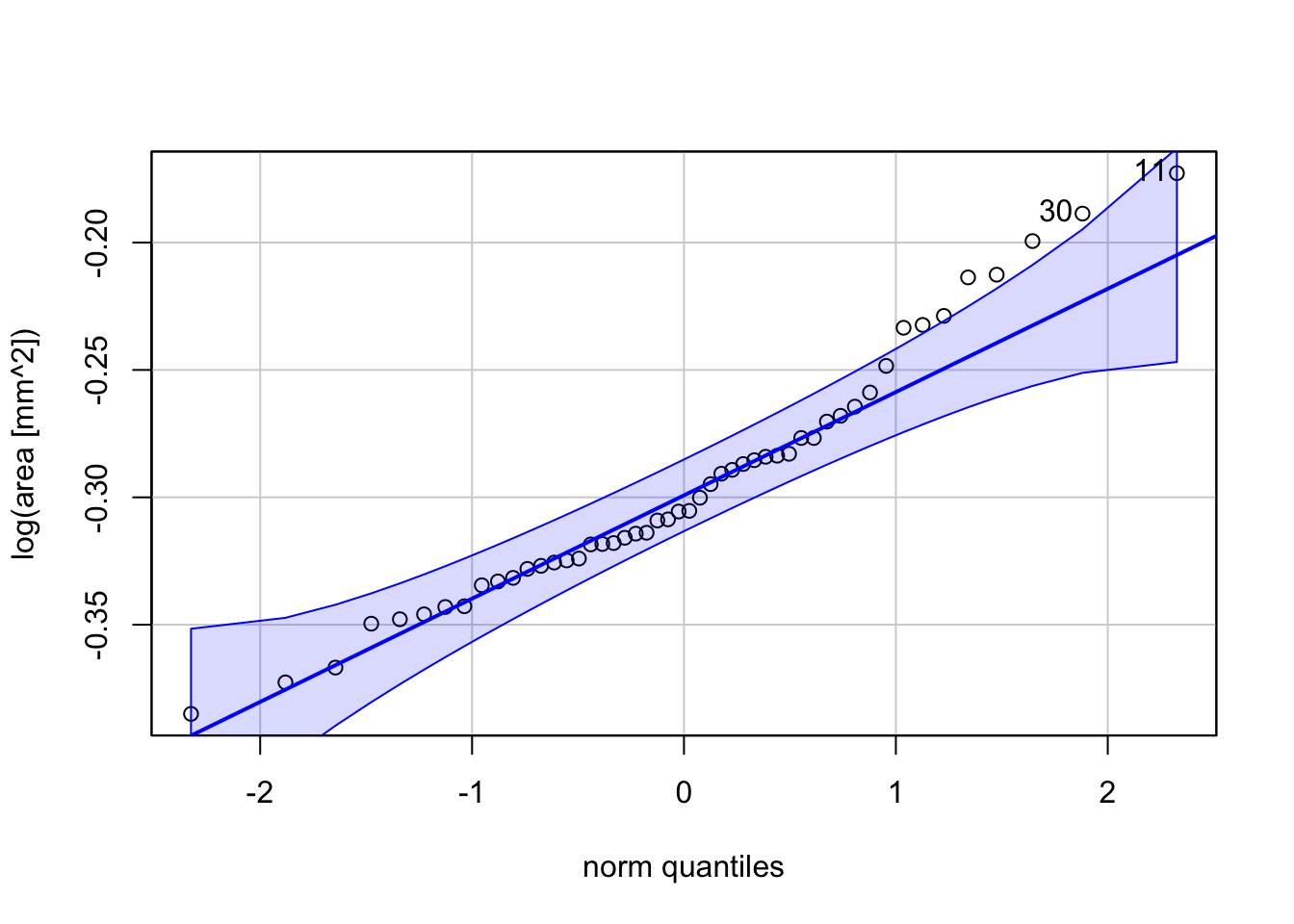
Figure 7.6: Graphique quantile-quantile comparant le log(area) en fonction d’une distribution normale obtenu à l’aide de car::qqPlot().
Interprétation
Si quasiment tous les points sont compris dans l’enveloppe de confiance à 95%, le graphique indique que les deux distributions ne sont pas fondamentalement différentes. Ici les points correspondants aux valeurs les plus élevées sortent de l’enveloppe pour un certain nombre d’entre eux d’affilée, et les points 11 et 30 sont considérés comme suspects. Ceci indique que les effectifs observés dans l’échantillon sont plus nombreux en queue droite de distribution que ce que la distribution normale prédit en théorie. Ceci confirme l’impression de distribution asymétrique et/ou bimodale. Il est probable qu’on ait au moins deux types d’œufs allongés différents dans l’échantillon, avec le second type moins nombreux, mais représenté par des œufs plus gros, ce qui enfle la partie droite de la distribution.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel A07La_distri2 (Distributions (suite)).
BioDataScience1::run("A07La_distri2")