9.2 ANOVA à un facteur

Au lieu de nous attaquer aux comparaisons deux à deux, nous pouvons considérer une hypothèse unique que les moyennes de \(k\) populations (nos quatre groupes différents de crabes, par exemple) sont toutes égales. L’hypothèse alternative sera qu’au moins une des moyennes diffère des autres (sans préciser laquelle). En formulation mathématique, cela donne :

\(H_0: \mu_1 = \mu_2 = ... = \mu_k\)
\(H_1: \exists(i, j) \mathrm{\ tel\ que\ } \mu_i \neq \mu_j\)

Notre hypothèse nulle est très restrictive, mais par contre, l’hypothèse alternative est très vague, car nous ne savons pas où sont les différences à ce stade si nous rejetons \(H_0\). Nous nous en occuperons plus tard.

Propriété d’additivité des parts de variance. La variance se calcule comme :

\[var_x = \frac{SCT}{ddl}\]

Avec \(SCT\), la somme des carrés totaux, soit \(\sum_{i = 1}^n (x_i - \bar{x})^2\), la somme des carrés des écarts à la moyenne générale. Les ddl sont les degrés de liberté déjà rencontrés à plusieurs reprises qui valent \(n - 1\) dans le cas de la variance d’un échantillon.

Cette variance peut être partitionnée. C’est-à-dire que, si la variance totale se mesure d’un point A à un point C, l’on peut mesurer la part de variance d’un point A à un point B, puis d’autre part, d’un point B à un point C, et dans ce cas,

\[SCT = SC_{A-C} = SC_{A-B} + SC_{B-C}\]

Cette propriété, dite d’additivité des variances, permet de décomposer la variance totale à souhait tout en sachant que la somme des différentes composantes donne toujours la même valeur que la variance totale.

À vous de jouer !

9.2.1 Modèle de l’ANOVA

Mais qu’est-ce que cette propriété d’additivité des variances vient faire ici ? Nous souhaitons comparer des moyennes, non ? Effectivement, mais considérons le modèle mathématique suivant :

\[y_{ij} = \mu + \tau_j + \epsilon_i \mathrm{\ avec\ } \epsilon \sim N(0, \sigma^2)\]

Avec l’indice \(j = 1 .. k\) populations et l’indice \(i = 1 .. n\) observations du jeu de données. Chaque observation \(y_{ij}\) correspond à deux écarts successifs de la moyenne globale \(\mu\) : une constante “tau” par population \(\tau_j\) d’une part et un terme \(\epsilon_i\) que l’on appelle les résidus et qui est propre à chaque observation individuelle. C’est ce dernier terme qui représente la partie statistique du modèle avec une distribution normale centrée sur zéro et avec une variance \(\sigma^2\) que nous admettrons constante et identique pour toutes les populations par construction.

Le graphique à la Fig. 9.3 représente une situation typique à trois sous-populations.

# Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
# ℹ Please use `linewidth` instead.
# This warning is displayed once every 8 hours.
# Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
# generated.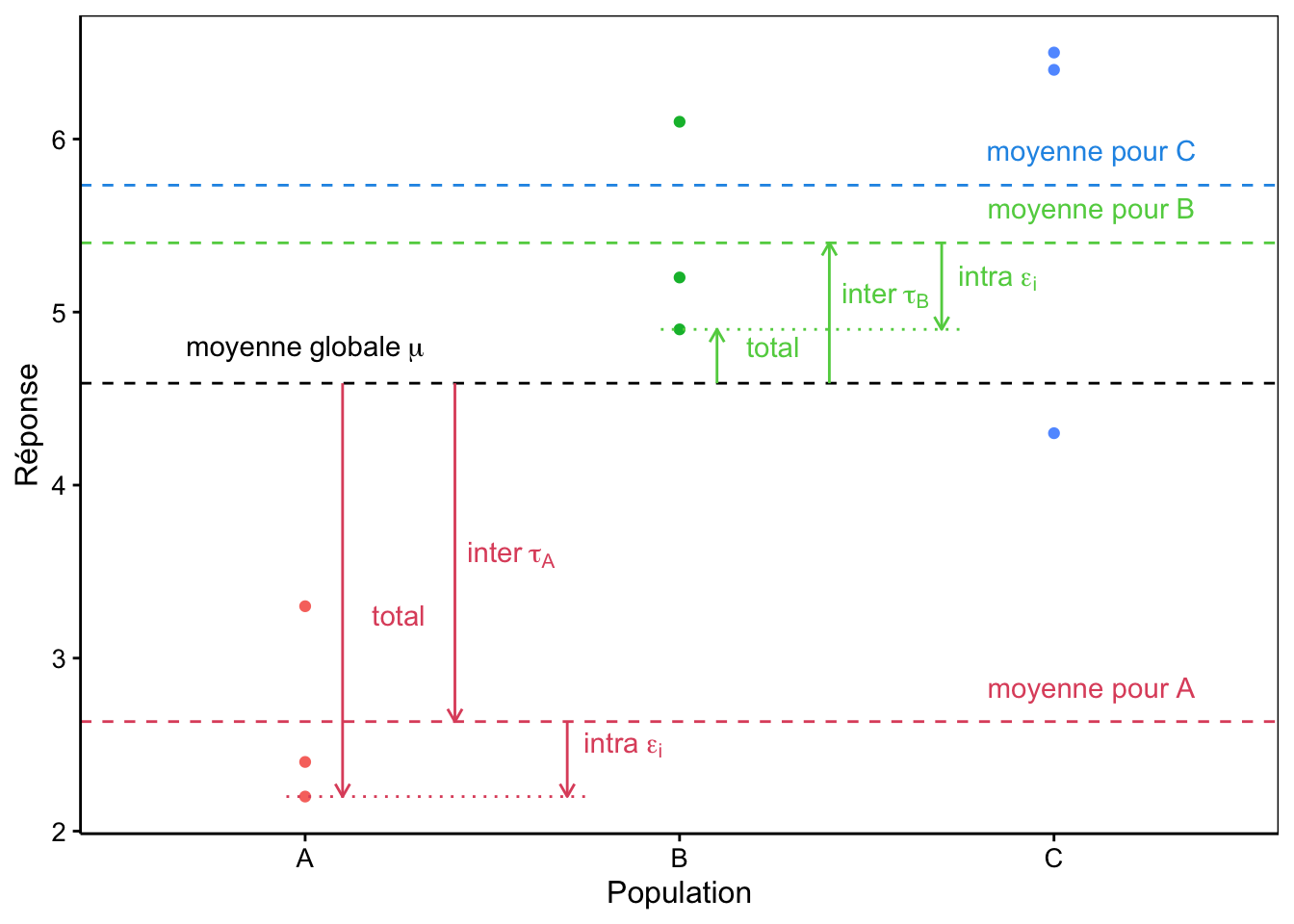

Figure 9.3: Décomposition de la variance dans un cas à trois populations A, B et C fictives.

Notons que ce modèle à trois termes représente bien la situation qui nous intéresse, mais aussi, qu’il décompose la variance totale (entre \(\mu\) et chaque point observé) en deux : ce que nous appellerons le terme inter représentant l’écart entre la moyenne globale \(\mu\) et la moyenne de la sous-population concernée (\(\tau_j\)) et le terme intra depuis cette moyenne de la sous-population jusqu’au point observé (\(\epsilon_i\)).

À vous de jouer !

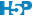
D’une part, nous nous trouvons dans une situation d’additivité de la variance si nous décidons de calculer ces “variance inter” et “variance intra”. D’autre part, sous \(H_0\) nous sommes sensés avoir toutes les moyennes égales à \(\mu\), et donc, tous les \(\tau_j = 0\). Donc, les valeurs non nulles de \(\tau_j\) ne doivent qu’être dues au hasard de l’échantillonnage et être par conséquent largement inférieures à la variabilité entre les individus, ou variance intra \(\epsilon_i\). La Fig. 9.4 représente deux cas avec à gauche une situation où \(H_0\) est plausible, et à droite une situation où elle est très peu plausible. Notez qu’à gauche la variation entre les observations (intra) est bien plus grande que l’écart entre les moyennes (inter), alors qu’à droite c’est l’inverse.

A. Cas fictif avec moyennes probablement égales entre populations (étalement des points bien plus large que l'écart entre les moyennes), B. cas où les moyennes sont probablement différentes (écart des moyennes "inter" bien plus grand que l'étalement des points en "intra"-population).

Figure 9.4: A. Cas fictif avec moyennes probablement égales entre populations (étalement des points bien plus large que l’écart entre les moyennes), B. cas où les moyennes sont probablement différentes (écart des moyennes “inter” bien plus grand que l’étalement des points en “intra”-population).

Intuitivement, une comparaison de “inter” et “intra” permet de différencier la situation de gauche de celle de droite dans la Fig. 9.4. Si cette comparaison est faite sous forme d’un ratio “inter”/“intra”, alors ce ratio sera faible et tendra vers zéro sous \(H_0\) (cas A), alors qu’il sera d’autant plus élevé que \(H_0\) devient de moins en moins plausible (cas B).

Calcul de l’ANOVA

Calcul des sommes des carrés (inter- et intragroupes). Considérant :

i = indice des observations au sein du jeu de données de 1 à n,
j = facteurs (sous-populations de 1 à k),
\(\bar{y}\) = moyenne générale de l’échantillon,
\(\bar{y_j}\) = moyenne de la j^ème population.

La somme des carrés inter \(SC_{inter}\) et la somme des carrés intra \(SC_{intra}\) se calculent comme suit :

\[ \begin{aligned} SC_{inter} = \sum_{i=1}^n{(\bar{y_j} - \bar{y})^2} && SC_{intra} = \sum_{i=1}^n{(y_{ij} - \bar{y_j})^2} \end{aligned} \]

À ces sommes des carrés, nous pouvons associer les degrés de liberté suivants :

k – 1 pour l’intergroupe
n – k pour l’intragroupe

Sachant que les parts de variances sont les \(\frac{SC}{ddl}\) et sont appelés “carrés moyens”, nous construisons ce qu’on appelle le tableau de l’ANOVA de la façon suivante :

Type	Ddl	Somme carrés	Carré moyen (CM)	Statistique F_obs	P (>F)
Inter (facteur)	k - 1	SC_inter	SC_inter/ddl_inter	CM_inter/CM_intra	…
Intra (résidus)	n - k	SC_intra	SC_intra/ddl_intra

La statistique F_obs est le rapport des carrés moyens inter/intra. Elle représente donc le ratio que nous avons évoqué plus haut comme moyen de quantifier l’écart par rapport à \(H_0\). Le test consiste à calculer la valeur P associée à cette statistique. Pour cela, il nous faut une distribution statistique théorique de F sous \(H_0\). C’est un biologiste - statisticien célèbre nommé Ronald Aylmer Fisher qui l’a calculée. Pour cette raison, elle s’appelle la distribution F de Fisher.

À vous de jouer !

9.2.2 Distribution F

La distribution F est une distribution asymétrique n’admettant que des valeurs nulles ou positives, d’une allure assez similaire à la distribution du \(\chi^2\) que nous avons étudié au module 7.5. Elle est appelée loi de Fisher, ou encore, loi de Fisher-Snedecor. Elle a une asymptote horizontale à \(+\infty\). La distribution F admet deux paramètres, respectivement les degrés de liberté au numérateur (inter) et au dénominateur (intra). La Fig. 9.5 représente la densité de probabilité d’une loi F typique⁵¹.

# Scale for x is already present.
# Adding another scale for x, which will replace the existing scale.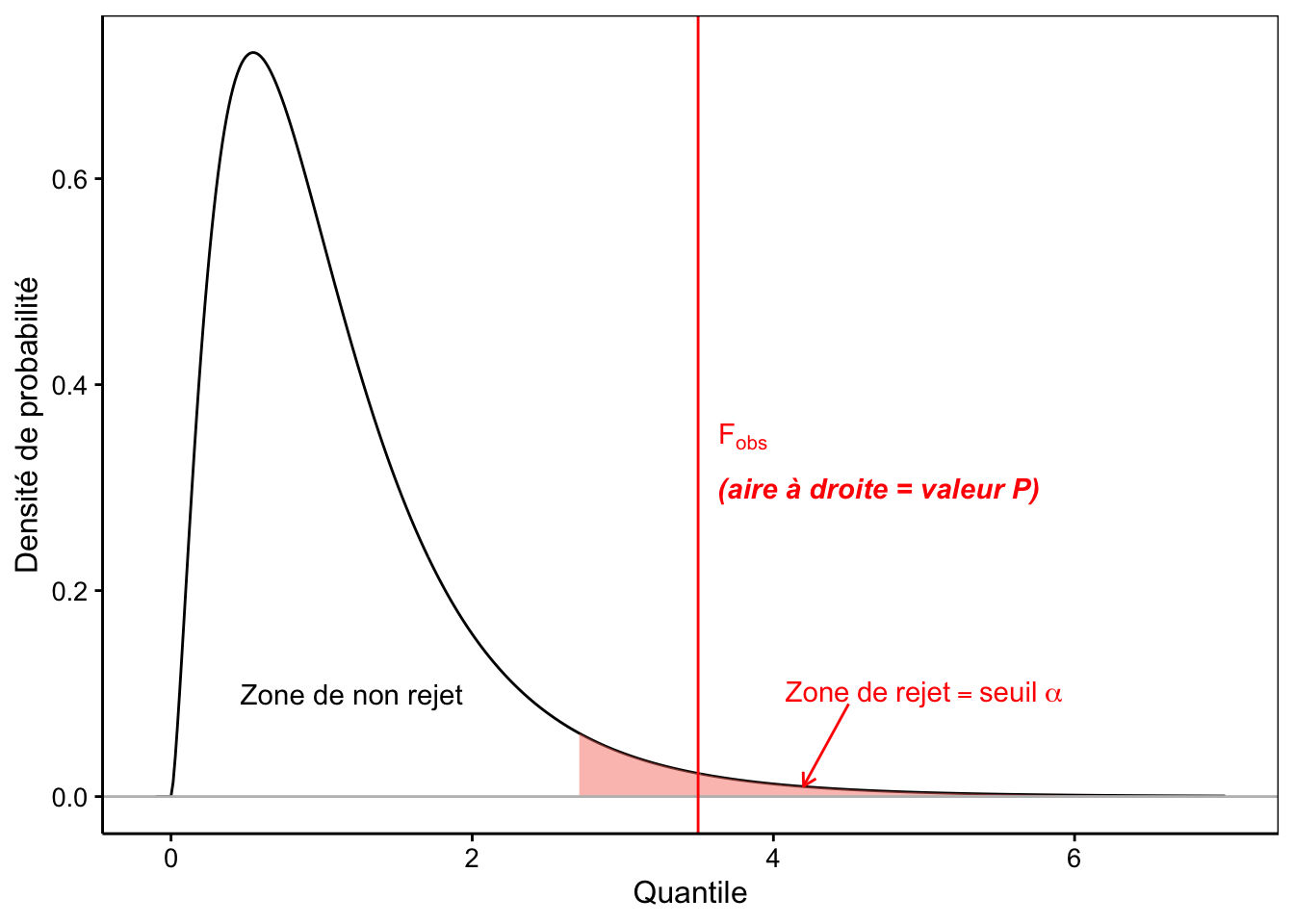

Allure typique de la densité de probabilité de la distribution F (ici ddl inter = 5 et ddl intra = 20). Plus *F~obs* est grand, plus l'hypothèse nulle est suspecte. La zone de rejet est donc positionnée à droite (en rouge).

Figure 9.5: Allure typique de la densité de probabilité de la distribution F (ici ddl inter = 5 et ddl intra = 20). Plus F~obs est grand, plus l’hypothèse nulle est suspecte. La zone de rejet est donc positionnée à droite (en rouge).

Nous commençons à avoir l’habitude maintenant. La valeur P est calculée comme l’aire à droite du quantile correspondant à F_obs. Enfin, nous rejetterons \(H_0\) seulement si la valeur P est inférieure au seuil \(\alpha\) qui a été choisi préalablement au test. Ceci revient à constater que, graphiquement, F_obs vient se positionner dans la zone de rejet en rouge comme sur la Fig. 9.5.

Lorsque nous réalisons une ANOVA, nous travaillons avec deux variables. La variable qualitative sert à découper l’échantillon en plusieurs sous-populations, alors que la variable quantitative est utilisée pour calculer les moyennes. Leurs rôles diffèrent donc, et elles ne sont bien évidemment pas interchangeables. En statistique, nous parlerons de variable réponse pour la variable qui mesure l’effet étudié et variable explicative pour la variable qui permet d’expliquer la réponse observée (et dans le cas de l’ANOVA, c’est le découpage en sous-populations).

Si le modèle est représenté par une formule dans R, la variable réponse sera à la gauche de la formule, et la (ou les) variable(s) explicative(s) à droite : var_réponse ~ var_explicative.

Conditions d’application

échantillon représentatif (par exemple, aléatoire),
observations indépendantes,
variable dite réponse quantitative,
une variable dite explicative qualitative à trois niveaux ou plus,
distribution normale des résidus \(\epsilon_i\),
homoscédasticité (même variance intragroupes, “homoscedasticity” en anglais, opposé à hétéroscédasticité = variance différente entre les groupes).

Les deux dernières conditions d’applications doivent être vérifiées. La normalité des résidus doit être rencontrée aussi bien que possible. Un graphique quantile-quantile des résidus permet de se faire une idée, comme sur la Fig. 9.6. Néanmoins, le test étant relativement robuste à des petites variations par rapport à la distribution normale, surtout si ces variations sont symétriques, nous ne serons pas excessivement stricts ici.

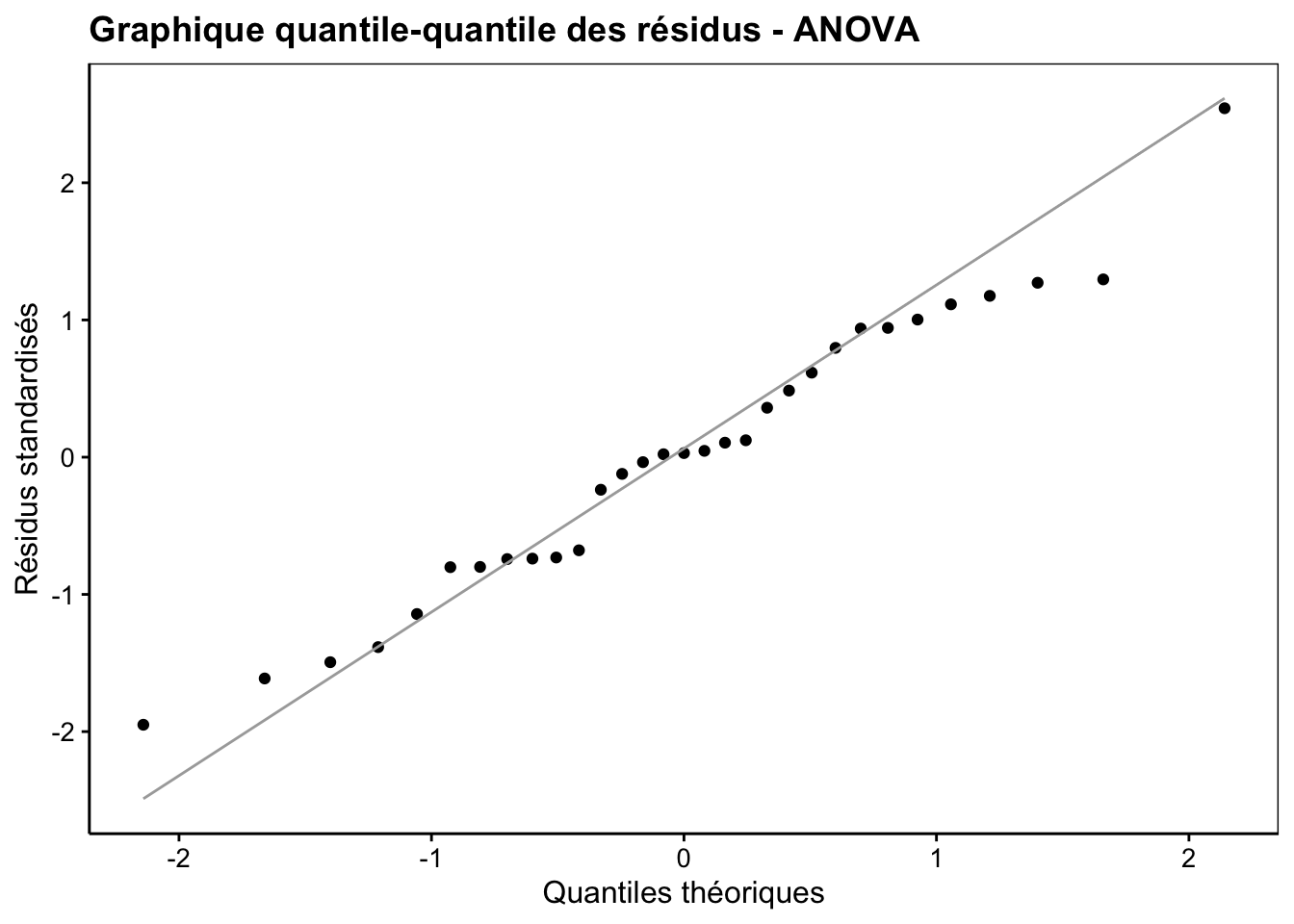
Figure 9.6: Graphique quantile-quantile appliqué aux résidus d’une ANOVA pour déterminer si leur distribution se rapproche d’un loi normale.

Pour rappel, ce graphique s’interprète comme suit : si les points s’alignent plutôt bien sur la droite, nous pouvons considérer que la distribution des résidus (ici la version standardisée, donc avec moyenne nulle et variance de un) est compatible avec la distribution théorique comparée qui est ici la distribution normale.

La condition d’homoscédasticité est plus sensible. Elle mérite donc d’être vérifiée systématiquement et précisément. Différents tests d’hypothèse existent pour le vérifier, comme le test de Bartlett, le test de Levene, etc. Nous vous proposons ici d’utiliser le test de Bartlett. Ses hypothèses sont :

\(H_0: var_1 = var_2 = ... = var_k\) (homoscédasticité)
\(H_1: \exists(i, j) \mathrm{\ tel\ que\ } var_i \neq var_j\) (hétéroscédasticité)

Si la valeur P est inférieure au seuil \(\alpha\) fixé au préalable, nous devrons rechercher une transformation des variables qui stabilisera la variance. La première transformation à essayer en biologie et la transformation logarithmique surtout si les valeurs négatives de la variable réponse ne sont pas possibles, signe d’une distribution qui est peut être plutôt de type log-normale pour cette variable. Si aucune transformation ne stabilise la variance, nous devrons nous rabattre vers un test non paramétrique équivalent, le test de Kruskal-Wallis que nous aborderons plus loin dans ce module. Il n’existe pas d’équivalent de l’ANOVA avec variances inégales, comme le test de Welch vs test t de Student classique dans le cas de la comparaison de deux moyennes.

À vous de jouer !

Résolution de notre exemple

Nous commençons par déterminer si nous avons une homoscédasticité. Considérons un seuil \(\alpha\) de 5% pour tous nos tests. Ensuite, nous utilisons bartlett.test() avec une formule qui représente bien la variable réponse en fonction de (le tilde ~) la variable explicative, soit ici, aspect ~ group :

bartlett.test(data = crabs2, aspect ~ group)

# 
#   Bartlett test of homogeneity of variances
# 
# data:  aspect by group
# Bartlett's K-squared = 24.532, df = 3, p-value = 1.935e-05

Nous rejetons \(H_0\). Il n’y a pas homoscédasticité. Calculons par exemple le logarithme népérien de aspect et réessayons :

crabs2 <- smutate(crabs2, log_aspect = ln(aspect))
bartlett.test(data = crabs2, log_aspect ~ group)

# 
#   Bartlett test of homogeneity of variances
# 
# data:  log_aspect by group
# Bartlett's K-squared = 37.891, df = 3, p-value = 2.981e-08

Ici cela ne fonctionne pas. Cela fait pire qu’avant. La transformation inverse (exp()) peut être essayée, mais ne stabilise pas suffisamment la variance. Après divers essais, il s’avère qu’une transformation puissance cinq stabilise bien la variance.

crabs2 <- smutate(crabs2, aspect5 = aspect^5)
bartlett.test(data = crabs2, aspect5 ~ group)

# 
#   Bartlett test of homogeneity of variances
# 
# data:  aspect5 by group
# Bartlett's K-squared = 1.7948, df = 3, p-value = 0.6161

La Fig. 9.7 montre la distribution dans les différents groupes de la variable transformée.

chart(data = crabs2, aspect5 ~ group) +
  geom_violin() +
  geom_jitter(width = 0.05, alpha = 0.5) +
  stat_summary(geom = "point", fun = "mean", color = "red", size = 3) +
  ylab("(ratio largeur arrière/max)^5")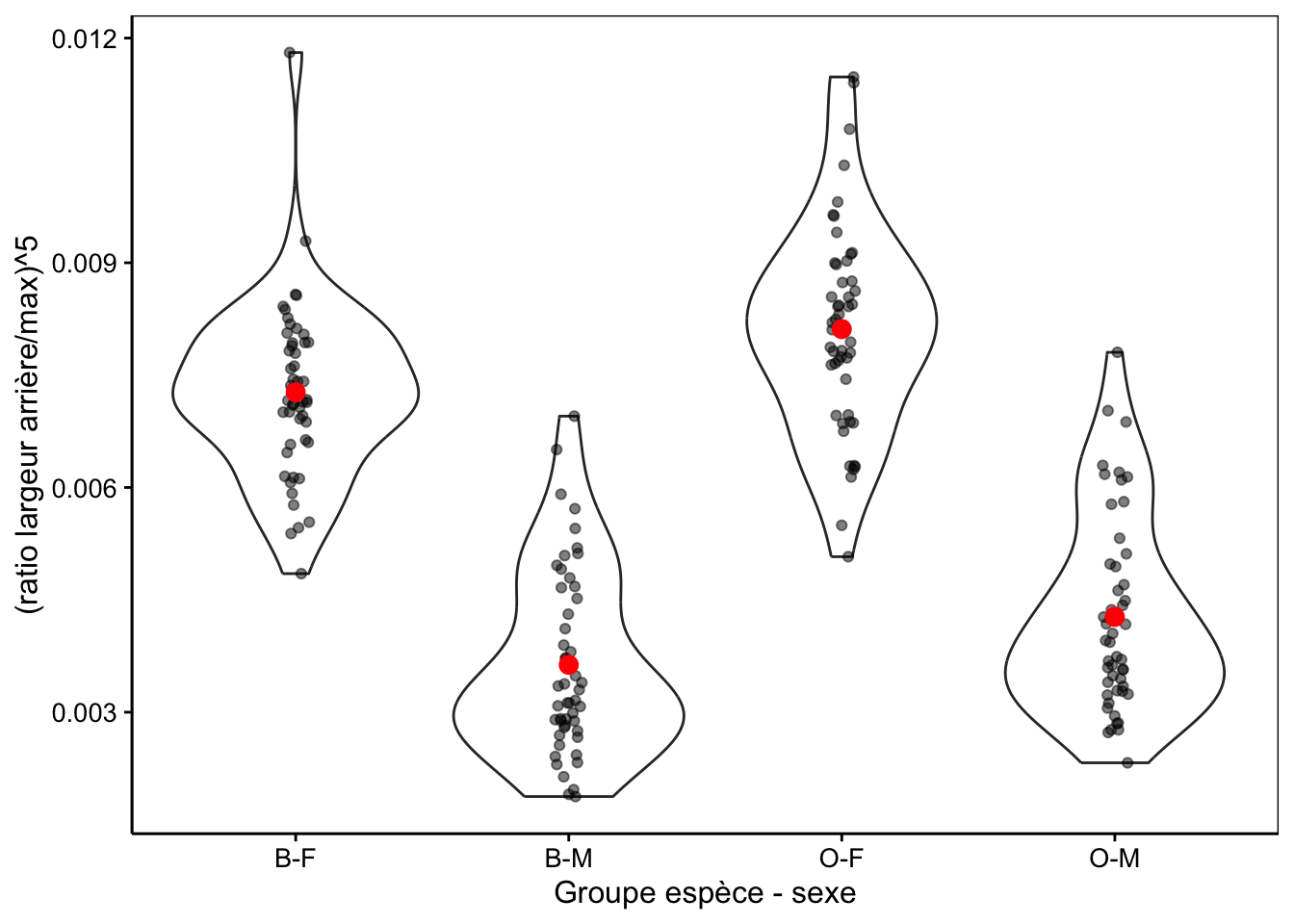

Figure 9.7: Transformation puissance cinq du ratio largeur arrière/largeur max en fonction du groupe de crabes L. variegatus.

Nous poursuivons sur une description des données utile pour l’ANOVA :

crabs2 %>.%
  sgroup_by(., group) %>.%
  ssummarise(.,
    mean  = fmean(aspect5),
    sd    = fsd(aspect5),
    count = fsum(!is.na(aspect5)))

#     group        mean          sd count
#    <fctr>       <num>       <num> <int>
# 1:    B-F 0.007270262 0.001148896    50
# 2:    B-M 0.003632440 0.001235495    50
# 3:    O-F 0.008114409 0.001384515    50
# 4:    O-M 0.004272370 0.001296139    50

Ensuite l’ANOVA proprement dite se réalise en deux étapes : (1) lm() calcule le modèle sur base d’une formule de type var_réponse ~ var_explicative (ici, aspect5 ~ group) et nous récupérons le résultat de ce calcul dans crabs2_anova pour utilisation ultérieure, et (2) la fonction anova() appliquée sur cet objet nous produit le tableau de l’ANOVA. Pour une version plus propre de ce tableau, nous utilisons enfin tabularise() :

anova(crabs2_anova <- lm(data = crabs2, aspect5 ~ group)) |> tabularise()

# Warning in set2(resolve(...)): The object is read-only and cannot be modified.
# If you have to modify it for a legitimate reason, call the method $lock(FALSE)
# on the object before $set(). Using $lock(FALSE) to modify the object will be
# enforced in future versions of knitr and this warning will become an error.

Analyse de la variance Réponse : aspect5
Terme	Ddl	Somme des carrés	Carrés moyens	Valeur de Fobs.	Valeur de p
group	3	0.000727	2.42·10-04	151	< 2·10-16	***
Résidus	196	0.000316	1.61·10-06
0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Nous observons dans le tableau de l’ANOVA que la valeur P est très faible et inférieure à \(\alpha\). Nous rejetons \(H_0\). Nous pouvons dire que le ratio largeur arrière / max à la puissance cinq diffère significativement entre les groupes (ANOVA, F = 150, ddl = 3 & 196, valeur P << 10^-3).

Ce n’est qu’une fois l’ANOVA réalisée que nous pouvons calculer et visionner la distribution des résidus à partir de notre objet crabs2_anova (Fig. 9.8).

chart$qqplot(crabs2_anova, lang = "fr")

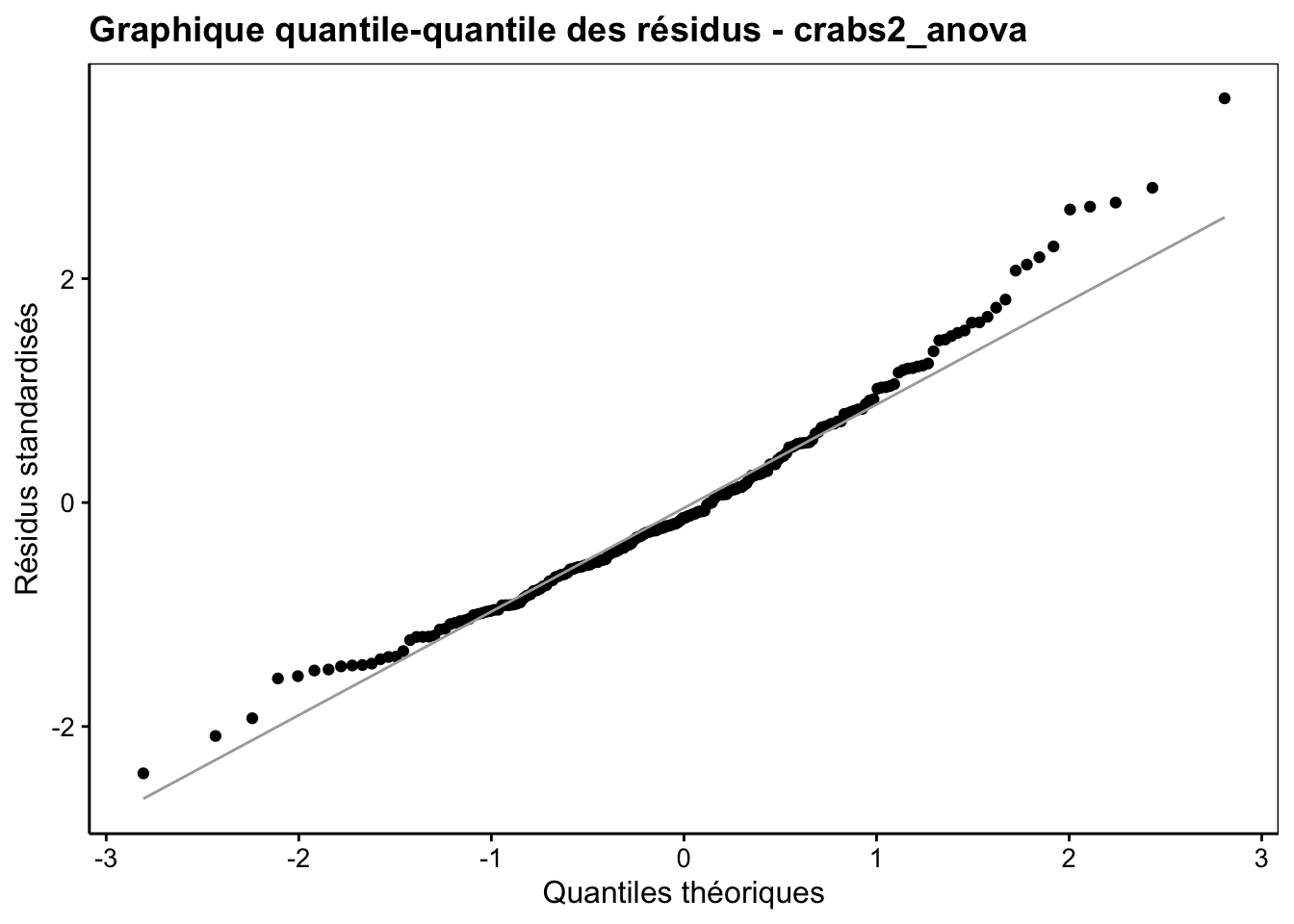
Figure 9.8: Graphique quantile-quantile des résidus pour l’analyse de aspect^5.

Cette distribution s’éloigne un peu aux extrêmes de la distribution normale. Nous sommes dans un cas un peu limite. Soit nous considérons que l’écart est suffisamment léger pour ne pas trop influer sur l’ANOVA, soit nous devons passer à un test non paramétrique. Nous ferons les deux ici à des fins de comparaison.

Pour en savoir plus

L’ANOVA expliquée en trois minutes
Introduction to ANOVA (en anglais). Part I, part II, part III, part IV, and part V.
Explication de l’analyse de variance en détaillant le calcul par la Kahn Academy. Partie I, partie II et partie III. Assez long : près de 3/4h en tout. Ne regardez que si vous n’avez pas compris ce que sont les sommes des carrés.

Les fonctions qui permettent les calculs relatifs à la distribution F dans R sont <q|p|r|d>f(). En outre, dist_f() génère un objet permettant d’en tracer facilement le graphique. Leur utilisation est similaire à celle des distributions vues au module 6.1.↩︎