9.3 Test “post-hoc”
Avec l’ANOVA, lorsque nous rejetons \(H_0\) comme dans le cas de notre exemple, nous savons qu’il y a au moins deux moyennes qui diffèrent l’une de l’autre, mais nous ne savons toujours pas lesquelles à ce stade. Notre analyse n’est pas terminée. Nous allons revisiter les tests de comparaison multiples deux à deux, mais en prenant des précautions particulières pour éviter l’inflation du risque d’erreur.
Tout d’abord, nous mettons en place un garde-fou. Nous effectuons toujours une ANOVA en premier lieu, et nous n’envisageons les comparaisons multiples que lorsque \(H_0\) est rejetée. Cela évite beaucoup de faux positifs. On appelle cela des tests “post hoc” car ils ne sont pas planifiés d’emblée, mais suivent un conclusion préalable (ici, le rejet de \(H_0\) dans un test ANOVA).
À vous de jouer !
Une approche simple consisterait à modifier notre seuil \(\alpha\) pour chaque test individuel vers le bas afin que le risque de se tromper dans au moins un des tests ne dépasse pas la valeur de \(/alpha\) que nous nous sommes fixée. C’est la correction de Bonferroni. Elle consiste à diviser la valeur de \(/alpha\) par le nombre de tests simultanés nécessaires, et d’utiliser cette valeur corrigée comme seuil \(\alpha\) de chaque test de Student individuel. Dans le cas de quatre populations, nous avons vu qu’il y a six comparaisons multiples deux à deux. Donc, en appliquant un seuil corrigé de \(\alpha/6 = 0,05 / 6 = 0,00833\) pour chaque test, on aura la probabilité suivante pour \(1 - \alpha\) :
\[(1 - 0,05/6)^6 = 0,951\]
Donc, le risque global pour l’ensemble des six tests est bien de 1 - 0,951 = 0,049, soit 5%. Si elle a le mérite d’être simple, cette façon de faire n’est pas considérée comme la plus efficace. Actuellement, la méthode HSD de Tukey est préférée. HSD veut dire “Honest Significant Difference”. La technique consiste à calculer l’écart minimal des moyennes pour considérer qu’elles sont significativement différentes l’une de l’autre. Ensuite, pour chaque comparaison deux à deux, l’écart entre les moyennes est comparé à cette valeur de référence52. Dans R, le test peut se visualiser soit sous une forme textuelle, soit sous une version graphique qui résume les comparaisons. Le code est un peu plus complexe et fait intervenir le package {multcomp}. Inspirez-vous de ce code dans vos projets.
# Version textuelle avec summary()
summary(crabs2_posthoc <- confint(multcomp::glht(crabs2_anova,
linfct = multcomp::mcp(group = "Tukey"))))#
# Simultaneous Tests for General Linear Hypotheses
#
# Multiple Comparisons of Means: Tukey Contrasts
#
#
# Fit: lm(formula = aspect5 ~ group, data = crabs2)
#
# Linear Hypotheses:
# Estimate Std. Error t value Pr(>|t|)
# B-M - B-F == 0 -0.0036378 0.0002538 -14.331 < 0.001 ***
# O-F - B-F == 0 0.0008441 0.0002538 3.326 0.00603 **
# O-M - B-F == 0 -0.0029979 0.0002538 -11.810 < 0.001 ***
# O-F - B-M == 0 0.0044820 0.0002538 17.657 < 0.001 ***
# O-M - B-M == 0 0.0006399 0.0002538 2.521 0.05948 .
# O-M - O-F == 0 -0.0038420 0.0002538 -15.136 < 0.001 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# (Adjusted p values reported -- single-step method)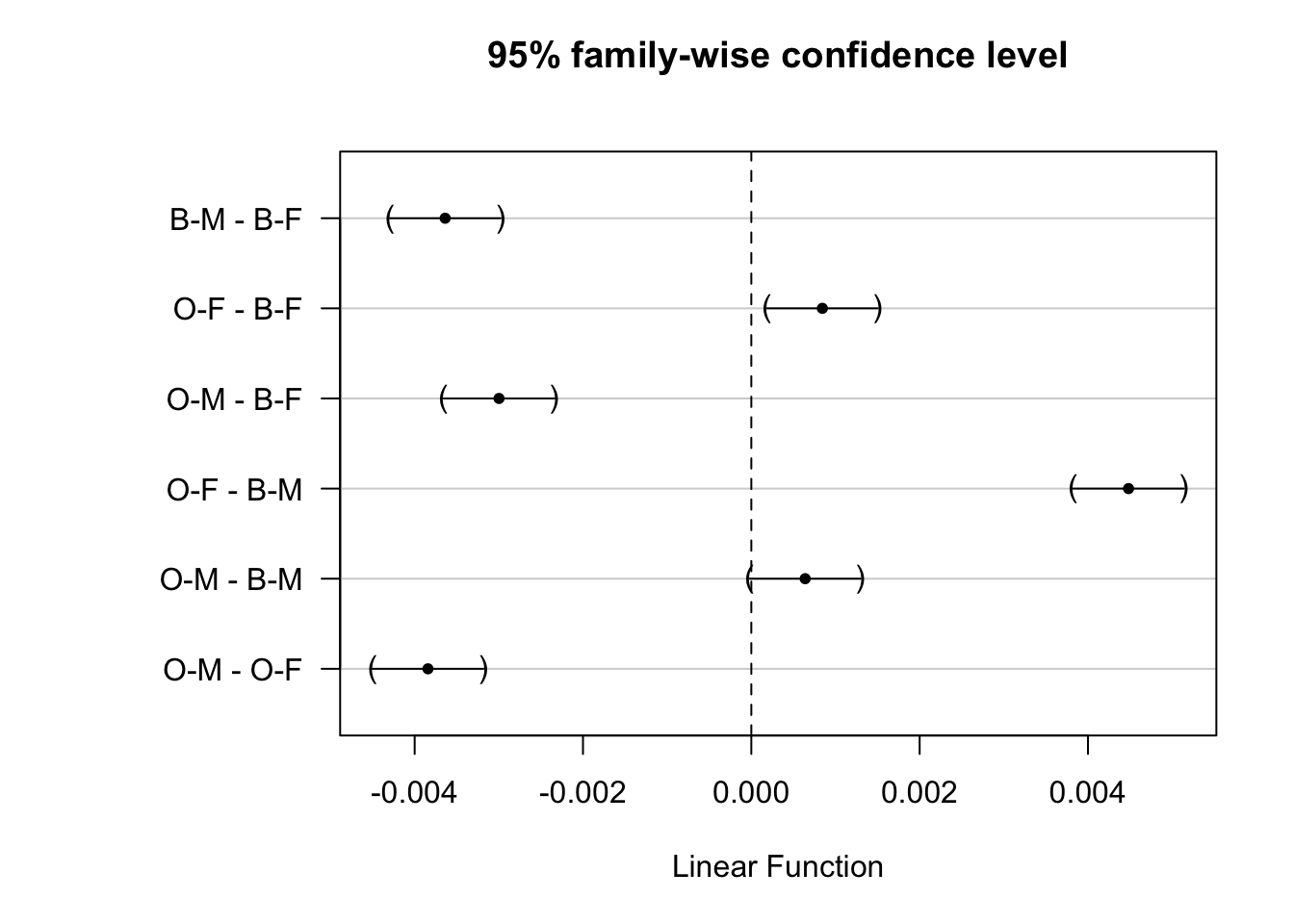
Avec la version textuelle, nous comparons comme à notre habitude les valeurs p renseignées dans la dernière colonne du tableau (nommée Pr(>|t|)) au seuil \(\alpha\) avec la règle habituelle de rejet si p < \(\alpha\) (donc, différence des moyennes de cette paire significative au seuil \(\alpha\) choisi). La comparaison se fait pour chaque ligne du tableau.
Avec la version graphique, les barres d’erreurs horizontales représentent les intervalles de confiance à \(1 - \alpha\) autour de la différence des moyennes pour la paire considérée (indiquée en libellé de l’axe des ordonnées). Si cet intervalle de confiance ne contient pas zéro (par ailleurs mis en évidence par un trait vertical pointillé sur le graphique), nous pourrons considérer que les deux moyennes diffèrent de manière significative au seuil \(\alpha\) choisi. Ici aussi, l’interprétation se fait ligne après ligne, c’est à dire, paire après paire.
Si nous gardons notre seuil \(\alpha\) de 5%, seuls les mâles ne diffèrent (tout juste) pas entre eux (ligne O-M - B-M dans la version textuelle et dans le graphique) avec une valeur p de 6%. Toutes les autres comparaisons deux à deux sont significativement différentes.
En conclusion, tous les groupes diffèrent de manière significative sauf les mâles (test HSD de Tukey, valeur p < 5%).
Conditions d’application
Les conditions d’application pour le test post hoc de Tukey sont les mêmes que pour l’ANOVA.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel A09La_anova (ANOVA et tests post-hoc).
BioDataScience1::run("A09La_anova")Réalisez le travail A09Ia_acidification.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques I : inférence à l’UMONS à terminer avant le 2025-03-31 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.