4.1 Observations dépendantes du temps
Démarrons tout de suite notre étude des séries chronologiques par plusieurs exemples concrets qui vont nous emmener dans les plaines enneigées du Grand Nord canadien, au sommet d’un volcan à Hawaï, dans le cerveau d’un patient épileptique ou au large de la mer Méditerranée.
Afin de configurer R pour utiliser le dialecte SciViews et charger les packages supplémentaires nécessaires à l’analyse de séries spatio-temporelles, vous entrez l’instruction suivante en début de script R, ou dans le chunk de “setup” d’un document R Markdown (aussi pour utiliser le français là où les traductions existent) :
4.1.1 Lynx
Vous vous intéressez au Lynx du Canada (Lynx canadensis) du point de vue de la dynamique de population à long terme de l’espèce. Afin de réaliser une étude rétrospective, vous recherchez la meilleure façon de déterminer la variation interannuelle de cette espèce à l’époque où elle était encore abondante (au 19e siècle et au début du 20e siècle).

Il apparaît que le nombre de lynx capturés par les trappeurs de l’époque est la meilleure information que vous puissiez obtenir (observations indirectes, ou “proxy” dans le jargon statisticien). La compilation de données de captures entre 1821 et 1934 en nombre d’individus donne ceci4 :
# [1] "tbl_ts" "tbl_df" "tbl" "data.frame"# # A tsibble: 114 x 2 [1Y]
# time trapping
# <dbl> <dbl>
# 1 1821 269
# 2 1822 321
# 3 1823 585
# 4 1824 871
# 5 1825 1475
# 6 1826 2821
# 7 1827 3928
# 8 1828 5943
# 9 1829 4950
# 10 1830 2577
# # ℹ 104 more rowsLe tableau brut des données n’est pas très parlant. Avec les séries chronologiques, c’est la représentation graphique qui révèle le mieux ce qu’il contient. Comme il y a continuité dans le temps entre les observations, le graphique le plus approprié ici utilise geom_line() au lieu du geom_point() auquel nous sommes habitués. Les traits entre les observations figurent cette continuité temporelle. Par convention, le temps se déroule de gauche à droite sur l’axe des abscisses. Cela donne ceci :
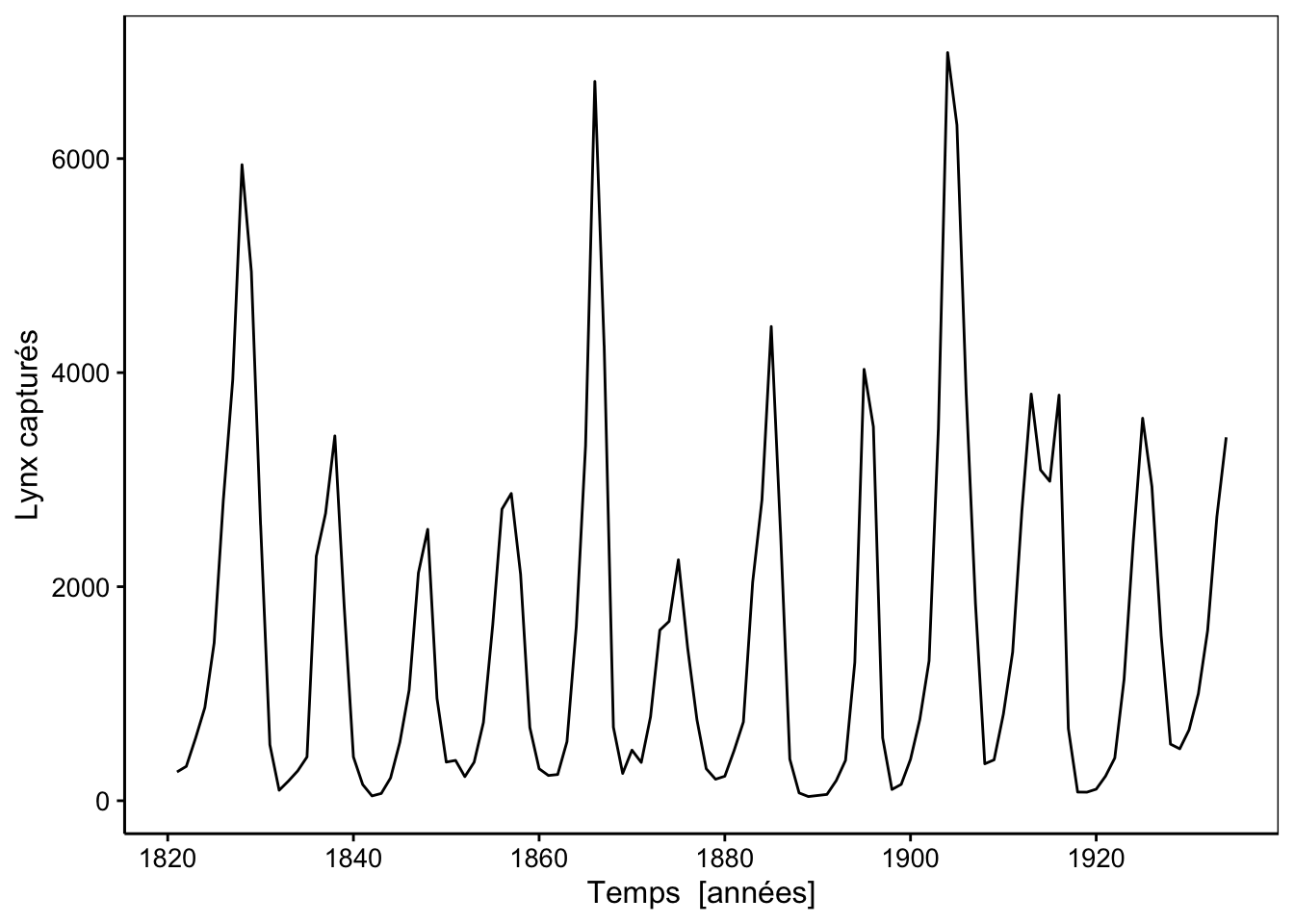
Nous sommes tout de suite surpris par la variation importante dans les captures d’une année à l’autre. Il semble que les années de captures abondantes reviennent à intervalle régulier. Mais comment analyser plus à fond ces données ? Notons d’emblée que l’unité d’échantillonnage (territoire Canadien) est la même pour chaque mesure. Donc, il n’y a pas indépendance des observations les unes par rapport aux autres. Intuitivement, nous pouvons d’ailleurs facilement imaginer cela. Connaissant les captures à une année, nous pouvons considérer que celles l’année d’avant ou l’année d’après ne sont pas complètement indépendantes, puisqu’il s’agit de la même population de lynx qui est échantillonnée. Cette continuité dans le temps doit être figurée sur le graphique en reliant les points. C’est donc une erreur de représenter une telle série chronologique à l’aide d’un nuage de points classique qui, quant à lui, figure des points séparés les uns des autres pour des observations indépendantes. Plus précisément, relier les points indique à la fois qu’il y a variation continue et aussi qu’il y a probablement un certain degré de dépendance entre les observations.
4.1.2 CO2 à Hawaï
Nous sommes en période de grands changements climatiques et de réchauffement planétaire, ce n’est plus un secret pour personne. Une des causes identifiées de ces changements est l’augmentation du CO2 dans l’atmosphère suite à la combustion massive d’énergie fossile (charbon, gaz et pétrole). Ces changements ont des effets bien visibles sur le vivant. En biologie, nous devons souvent confronter nos observations par rapport aux changements du milieu, et donc, nous manipulons fréquemment des séries chronologiques de données physico-chimiques. Le CO2 (en ppm ou parties par million) a été mesuré dans l’atmosphère au laboratoire NOAA situé en haut du volcan Mauna Loa à Hawaï.

co2.Cet observatoire est situé dans une zone suffisamment éloignée des principales sources industrielles de production de CO2, en plein milieu de l’Océan Pacifique, pour que les mesures n’en soient pas affectées directement, ou de manière négligeable. Les données suivantes présentent l’évolution du CO2 atmosphérique entre 1959 et 1998 :
# [1] "ts"# Jan Feb Mar Apr May Jun Jul Aug Sep Oct
# 1959 315.42 316.31 316.50 317.56 318.13 318.00 316.39 314.65 313.68 313.18
# 1960 316.27 316.81 317.42 318.87 319.87 319.43 318.01 315.74 314.00 313.68
# 1961 316.73 317.54 318.38 319.31 320.42 319.61 318.42 316.63 314.83 315.16
# 1962 317.78 318.40 319.53 320.42 320.85 320.45 319.45 317.25 316.11 315.27
# 1963 318.58 318.92 319.70 321.22 322.08 321.31 319.58 317.61 316.05 315.83
# 1964 319.41 320.07 320.74 321.40 322.06 321.73 320.27 318.54 316.54 316.71
# 1965 319.27 320.28 320.73 321.97 322.00 321.71 321.05 318.71 317.66 317.14
# 1966 320.46 321.43 322.23 323.54 323.91 323.59 322.24 320.20 318.48 317.94
# 1967 322.17 322.34 322.88 324.25 324.83 323.93 322.38 320.76 319.10 319.24
# 1968 322.40 322.99 323.73 324.86 325.40 325.20 323.98 321.95 320.18 320.09
# 1969 323.83 324.26 325.47 326.50 327.21 326.54 325.72 323.50 322.22 321.62
# 1970 324.89 325.82 326.77 327.97 327.91 327.50 326.18 324.53 322.93 322.90
# 1971 326.01 326.51 327.01 327.62 328.76 328.40 327.20 325.27 323.20 323.40
# 1972 326.60 327.47 327.58 329.56 329.90 328.92 327.88 326.16 324.68 325.04
# 1973 328.37 329.40 330.14 331.33 332.31 331.90 330.70 329.15 327.35 327.02
# 1974 329.18 330.55 331.32 332.48 332.92 332.08 331.01 329.23 327.27 327.21
# 1975 330.23 331.25 331.87 333.14 333.80 333.43 331.73 329.90 328.40 328.17
# 1976 331.58 332.39 333.33 334.41 334.71 334.17 332.89 330.77 329.14 328.78
# 1977 332.75 333.24 334.53 335.90 336.57 336.10 334.76 332.59 331.42 330.98
# 1978 334.80 335.22 336.47 337.59 337.84 337.72 336.37 334.51 332.60 332.38
# 1979 336.05 336.59 337.79 338.71 339.30 339.12 337.56 335.92 333.75 333.70
# 1980 337.84 338.19 339.91 340.60 341.29 341.00 339.39 337.43 335.72 335.84
# 1981 339.06 340.30 341.21 342.33 342.74 342.08 340.32 338.26 336.52 336.68
# 1982 340.57 341.44 342.53 343.39 343.96 343.18 341.88 339.65 337.81 337.69
# 1983 341.20 342.35 342.93 344.77 345.58 345.14 343.81 342.21 339.69 339.82
# 1984 343.52 344.33 345.11 346.88 347.25 346.62 345.22 343.11 340.90 341.18
# 1985 344.79 345.82 347.25 348.17 348.74 348.07 346.38 344.51 342.92 342.62
# 1986 346.11 346.78 347.68 349.37 350.03 349.37 347.76 345.73 344.68 343.99
# 1987 347.84 348.29 349.23 350.80 351.66 351.07 349.33 347.92 346.27 346.18
# 1988 350.25 351.54 352.05 353.41 354.04 353.62 352.22 350.27 348.55 348.72
# 1989 352.60 352.92 353.53 355.26 355.52 354.97 353.75 351.52 349.64 349.83
# 1990 353.50 354.55 355.23 356.04 357.00 356.07 354.67 352.76 350.82 351.04
# 1991 354.59 355.63 357.03 358.48 359.22 358.12 356.06 353.92 352.05 352.11
# 1992 355.88 356.63 357.72 359.07 359.58 359.17 356.94 354.92 352.94 353.23
# 1993 356.63 357.10 358.32 359.41 360.23 359.55 357.53 355.48 353.67 353.95
# 1994 358.34 358.89 359.95 361.25 361.67 360.94 359.55 357.49 355.84 356.00
# 1995 359.98 361.03 361.66 363.48 363.82 363.30 361.94 359.50 358.11 357.80
# 1996 362.09 363.29 364.06 364.76 365.45 365.01 363.70 361.54 359.51 359.65
# 1997 363.23 364.06 364.61 366.40 366.84 365.68 364.52 362.57 360.24 360.83
# Nov Dec
# 1959 314.66 315.43
# 1960 314.84 316.03
# 1961 315.94 316.85
# 1962 316.53 317.53
# 1963 316.91 318.20
# 1964 317.53 318.55
# 1965 318.70 319.25
# 1966 319.63 320.87
# 1967 320.56 321.80
# 1968 321.16 322.74
# 1969 322.69 323.95
# 1970 323.85 324.96
# 1971 324.63 325.85
# 1972 326.34 327.39
# 1973 327.99 328.48
# 1974 328.29 329.41
# 1975 329.32 330.59
# 1976 330.14 331.52
# 1977 332.24 333.68
# 1978 333.75 334.78
# 1979 335.12 336.56
# 1980 336.93 338.04
# 1981 338.19 339.44
# 1982 339.09 340.32
# 1983 340.98 342.82
# 1984 342.80 344.04
# 1985 344.06 345.38
# 1986 345.48 346.72
# 1987 347.64 348.78
# 1988 349.91 351.18
# 1989 351.14 352.37
# 1990 352.69 354.07
# 1991 353.64 354.89
# 1992 354.09 355.33
# 1993 355.30 356.78
# 1994 357.59 359.05
# 1995 359.61 360.74
# 1996 360.80 362.38
# 1997 362.49 364.34Notez bien qu’ici, les données sont dans un autre format, un objet de classe ts. Ce sont les données de séries temporelles régulières de R de base. Nous pouvons appliquer la fonction R de base plot() pour en faire le graphique (et cette fonction relie les points automatiquement comme vous pouvez le constater) :
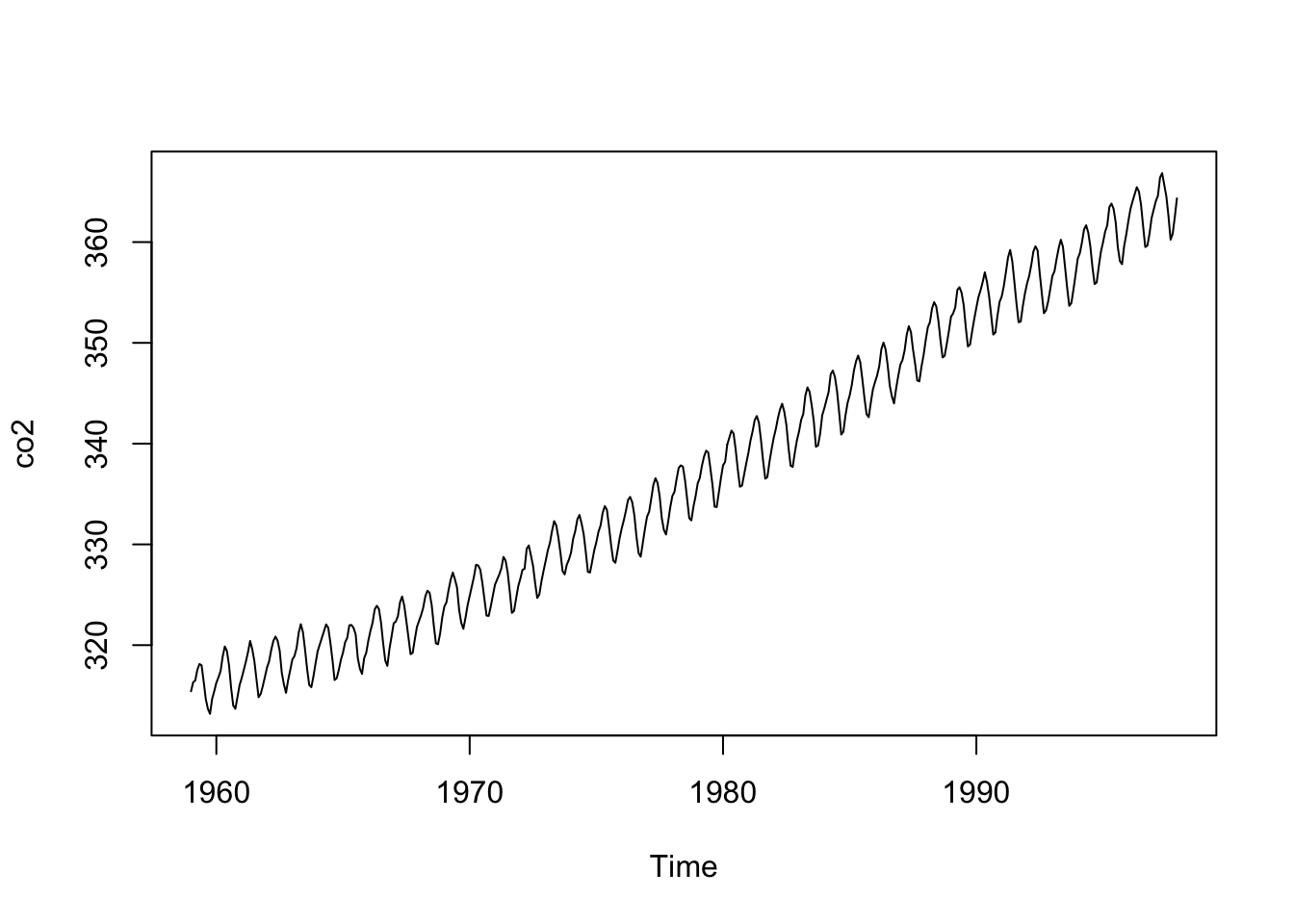
Les libellés des axes ne sont pas parfaits, mais les arguments xlab = et ylab = de la fonction plot() nous permettons de les redéfinir. Ici, nous en profitons pour découvrir qu’il est possible de formater ce texte à l’aide de expression(). Pour mettre le “2” en indice dans “CO2”, on écrira CO[2]. Pour tous les autres formatages possibles, voir ?plotmath.
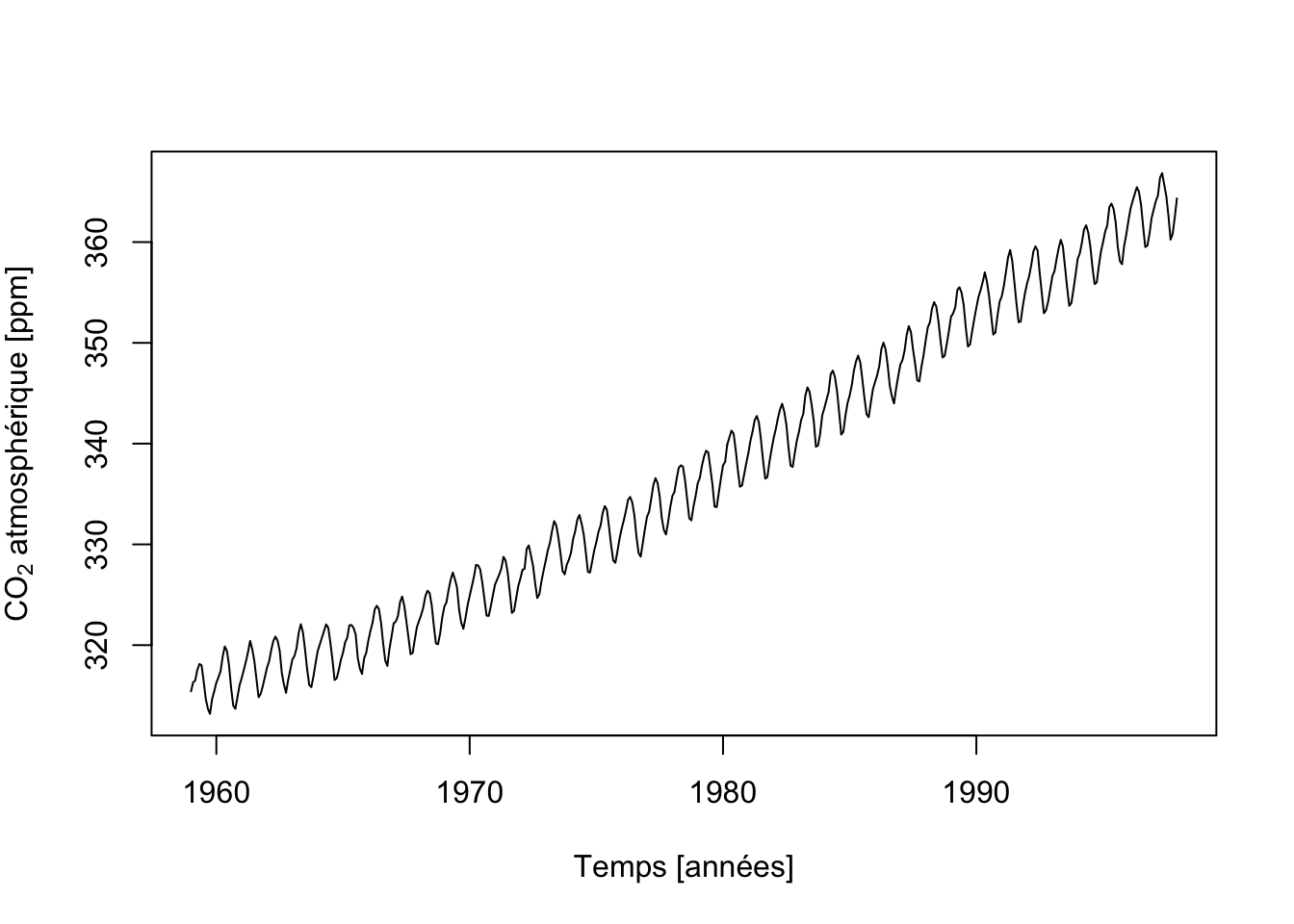
Si nous voulons utiliser chart(), il nous faut d’abord transformer nos données en tsibble à l’aide de tsibble::as_tsibble() :
# # A tsibble: 468 x 2 [1M]
# index value
# <mth> <dbl>
# 1 1959 Jan 315.
# 2 1959 Feb 316.
# 3 1959 Mar 316.
# 4 1959 Apr 318.
# 5 1959 May 318.
# 6 1959 Jun 318
# 7 1959 Jul 316.
# 8 1959 Aug 315.
# 9 1959 Sep 314.
# 10 1959 Oct 313.
# # ℹ 458 more rowsNotez que sans en changer le nom (pour lynx, nous avions du code qui le faisait et rajoutait aussi les labels des variables de manière transparente), les colonnes sont par défaut :
- index pour la colonne du temps
- value pour la colonne des données observées.
De plus, la date est un objet yearmonth que chart() n’apprécie pas trop. Donc, nous le transformons en Date avec as.Date().
chart(co2_tsbl, value ~ as.Date(index)) +
geom_line() +
labs(x = "Temps [années]", y = expression(paste(CO[2], " atmosphérique [ppm]")))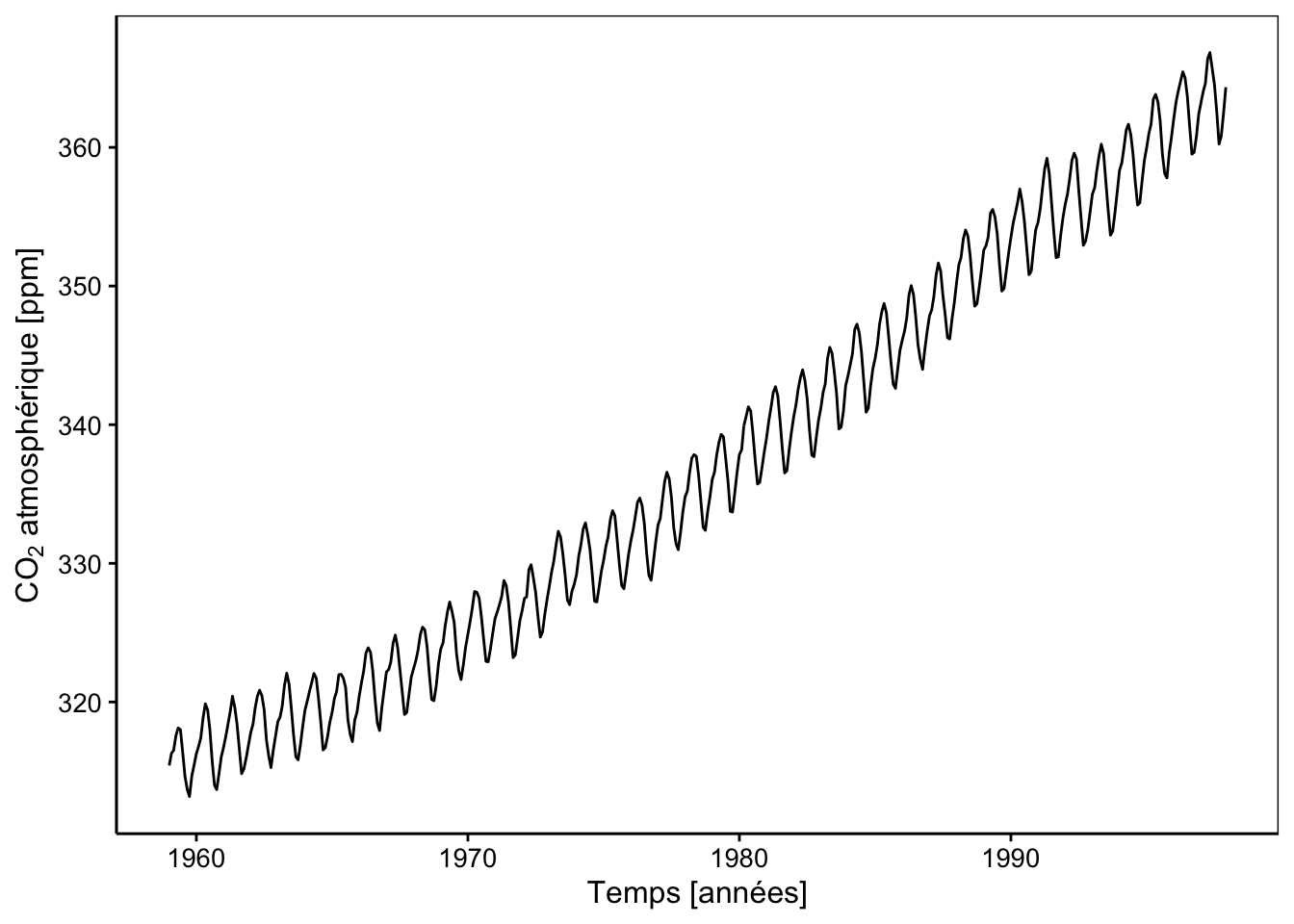
Ici aussi, nous observons très clairement des variations qui se répètent à intervalle régulier, probablement des variations saisonnières. Mais par-dessus ces fluctuations, une augmentation à plus long terme est effectivement particulièrement visible. Une fois de plus, les différentes observations ont toutes été réalisées au même endroit et une forte interdépendance est à suspecter entre les observations successives.
4.1.3 EEG
L’électro-encéphalogramme consiste à mesurer de manière non invasive l’activité électrique de notre cerveau. L’épilepsie est un dérèglement majeur du fonctionnement cérébral qui se marque particulièrement bien au niveau de l’EEG.
Le graphique suivant montre à quoi ressemble un signal enregistré par un EEG pendant une crise d’épilepsie (sachant qu’il y a autant de signaux différents que d’électrodes utilisées) :
# [1] "ts"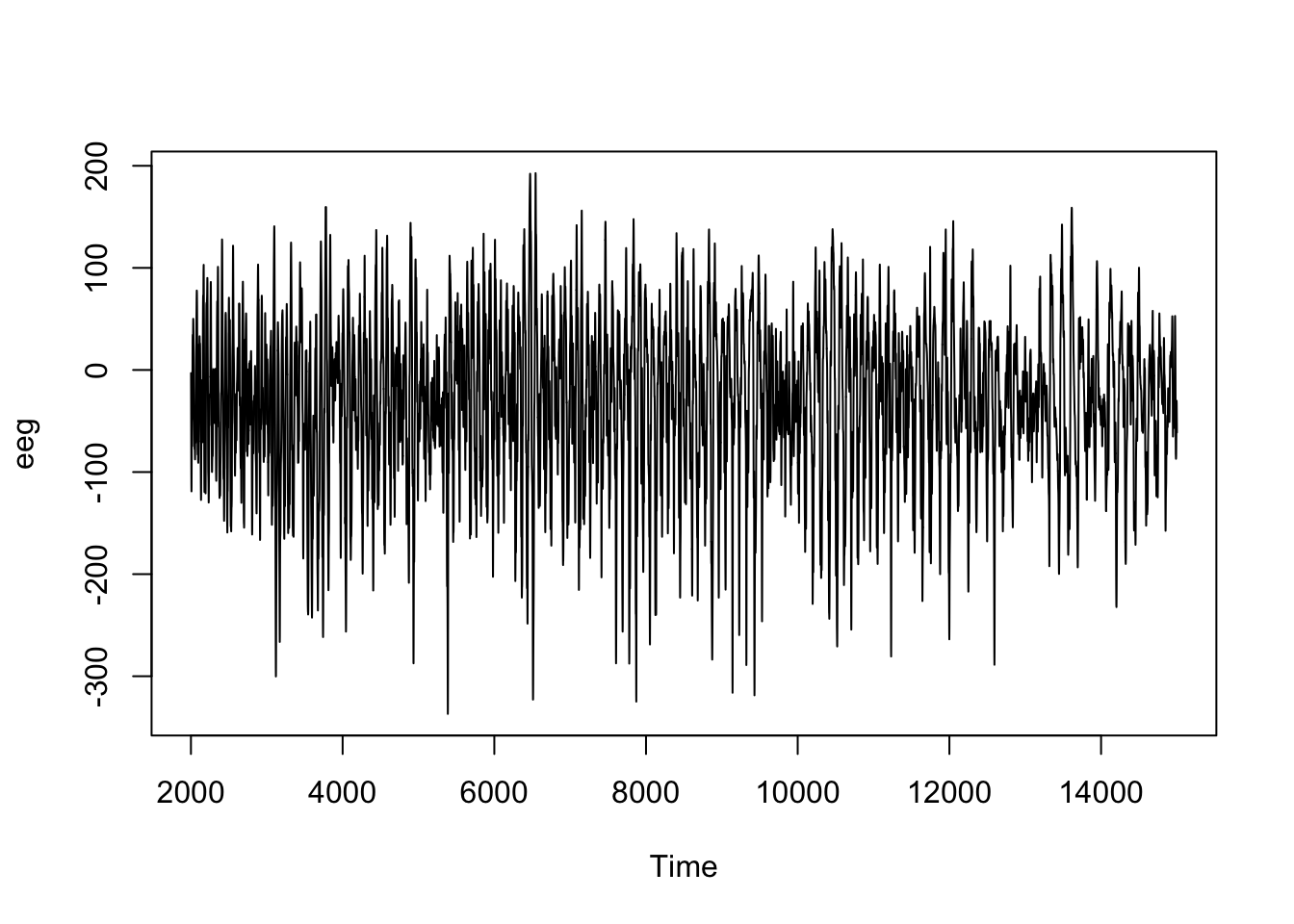
Cette série chronologique est comptabilisée sur l’axe du temps simplement avec le numéro de la mesure commençant par 2001, mais en réalité, 256 mesures sont réalisées par seconde ici. Dans cette série, les fluctuations sont importantes, mais apparaissent difficiles à interpréter sur le graphique brut.
4.1.4 Plancton méditerranéen
Les séries chronologiques sont aussi appelées séries spatio-temporelles, car sous certaines conditions, elles peuvent aussi servir à représenter des évènements qui varient spatialement, voir dans l’espace et le temps simultanément. Mais attention, quand nous parlons de variation spatiale, il ne peut s’agir que de variation unidimensionnelle, par exemple, le long d’un transect (tracé rectiligne ou non entre deux points et le long duquel les mesures sont réalisées). Un bon exemple d’une telle variation spatio-temporelle est représenté par l’étude du plancton en mer Méditerranée entre Nice et la Corse.
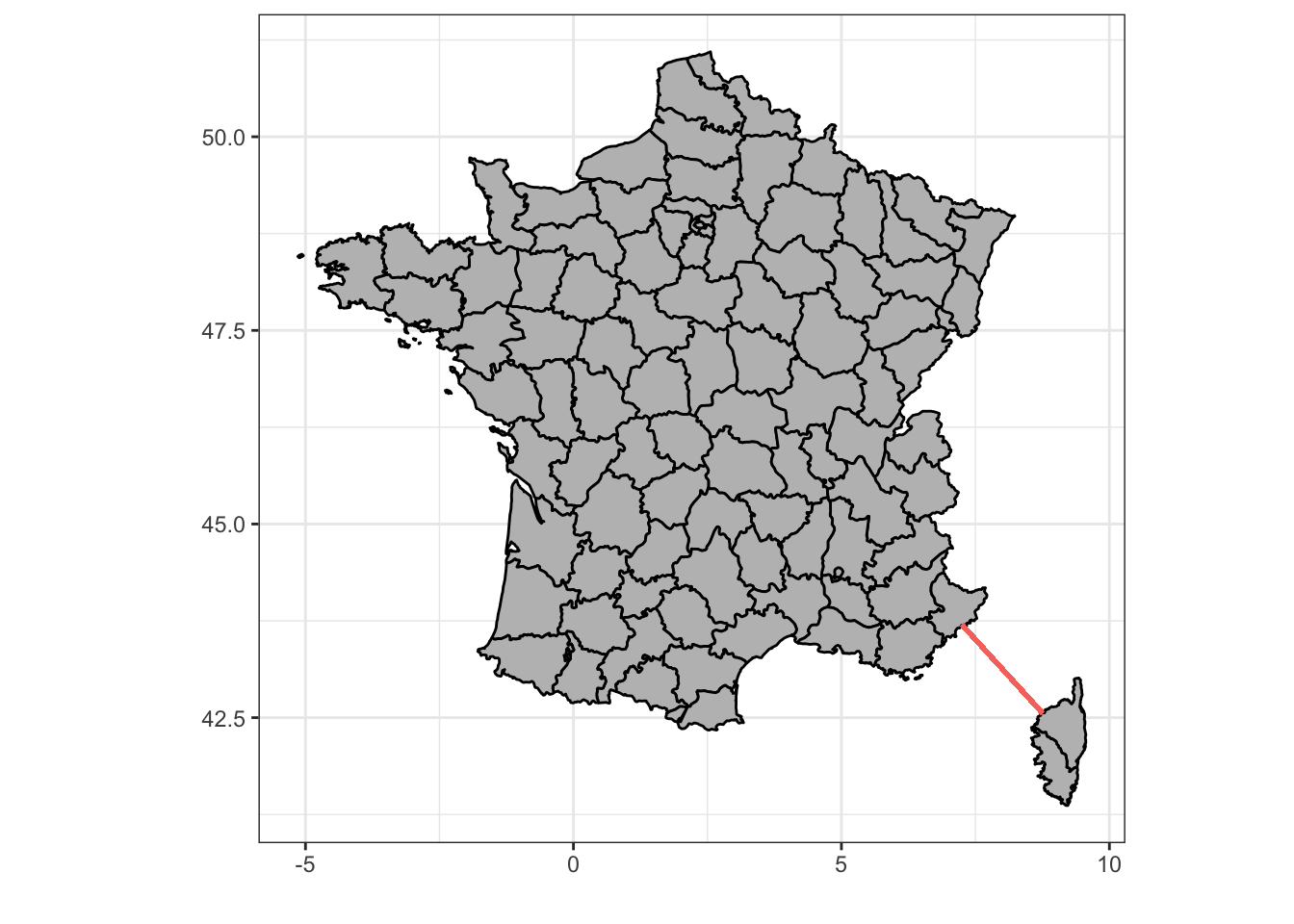
Figure 4.1: Une séries de 68 stations équiréparties le long d’un transect entre Nice et la Corse (trait rouge) sont échantillonnées pour la physico-chimie (marphy) et le plancton (marbio).
Nous avons ici effectivement un axe qui varie spatialement le long du transect, mais en même temps dans le temps, car les 68 stations ne sont pas échantillonnées simultanément, mais successivement dans le temps au fur et à mesure que le navire océanographique fait route entre Nice et Calvi en Corse. Nous avons déjà utilisé ces données au cours SDD II pour illustrer les analyses multivariées. Voyons ce que donnent les paramètres physico-chimiques sous forme de séries spatio-temporelles (notez que, comme marphy est un objet data.table, nous utilisons la fonction tsibble::as_tsibble() ou ts() pour le transformer en séries spatio-temporelles, plus de détails sur ces dernières fonctions seront donnés plus loin ; ici la colonne Station doit être créée d’abord et indiquée comme étant l’index à tsibble::as_tsibble()) :
read("marphy", package = "pastecs") %>.%
smutate(., Station = 1:nrow(.)) %>.%
tsibble::as_tsibble(., index = Station) %->%
marphy_tsbl
marphy_tsbl# # A tsibble: 68 x 5 [1]
# Temperature Salinity Fluorescence Density Station
# <dbl> <dbl> <dbl> <dbl> <int>
# 1 13.1 38.2 0.958 28.8 1
# 2 13.1 38.2 0.931 28.8 2
# 3 13.1 38.2 0.844 28.8 3
# 4 13.1 38.2 0.755 28.8 4
# 5 13.1 38.1 0.742 28.8 5
# 6 13.1 38.1 0.874 28.8 6
# 7 13.0 38.1 1.05 28.8 7
# 8 13.0 38.1 0.974 28.8 8
# 9 13.0 38.2 1.10 28.9 9
# 10 13.1 38.2 0.945 28.9 10
# # ℹ 58 more rows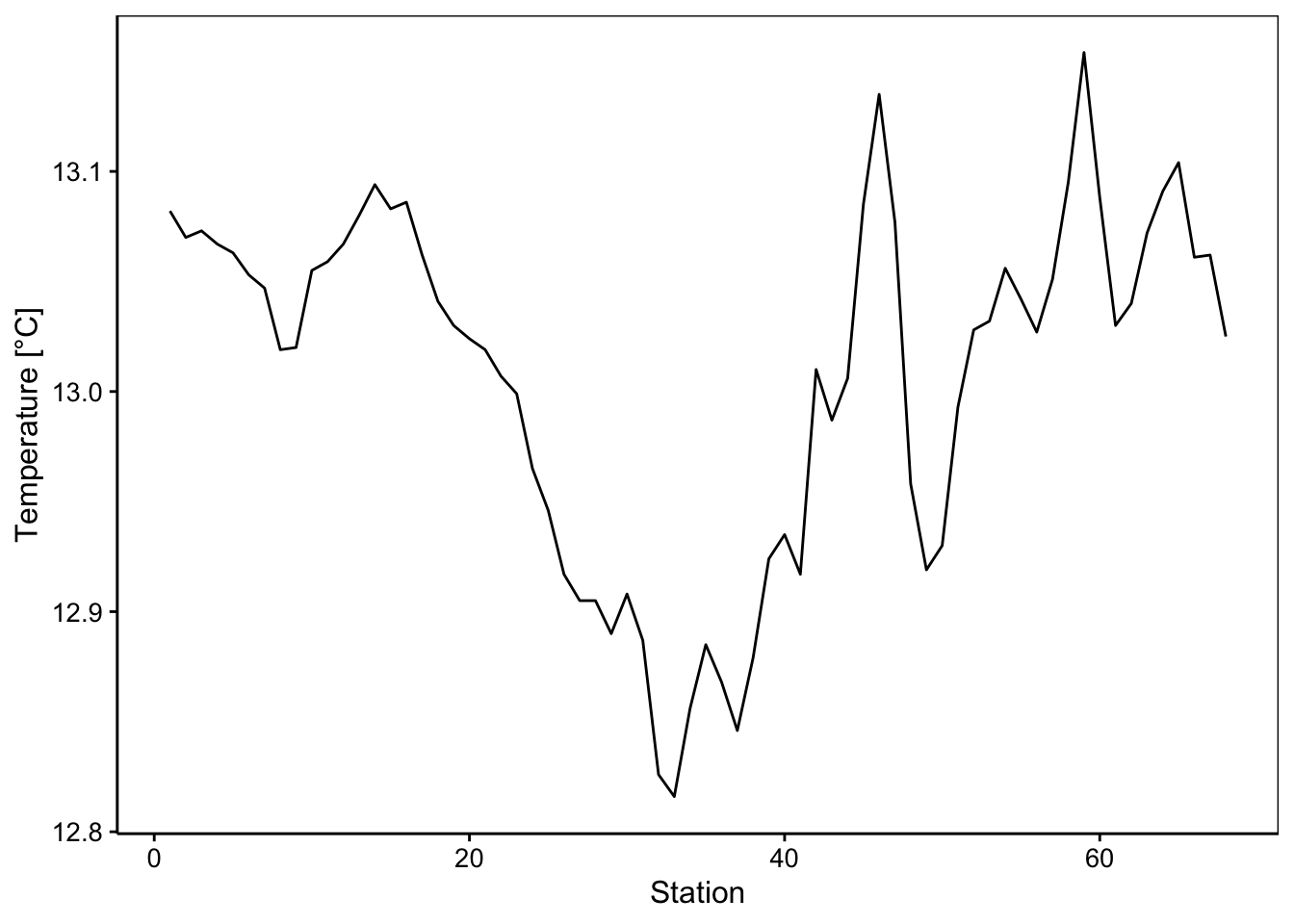
Nous avons ici plusieurs variables mesurées aux mêmes stations. La transformation avec ts() nous donne alors un objet mts() (“multiple time series”), avec un graphique via plot() qui est plutôt intéressant :
# [1] "mts" "ts" "matrix"# Time Series:
# Start = 1
# End = 68
# Frequency = 1
# Temperature Salinity Fluorescence Density
# 1 13.082 38.166 0.958 28.8436
# 2 13.070 38.162 0.931 28.8430
# 3 13.073 38.157 0.844 28.8385
# 4 13.067 38.150 0.755 28.8344
# 5 13.063 38.141 0.742 28.8282
# 6 13.053 38.129 0.874 28.8210
# 7 13.047 38.116 1.053 28.8122
# 8 13.019 38.131 0.974 28.8296
# 9 13.020 38.162 1.096 28.8534
# 10 13.055 38.175 0.945 28.8562
# 11 13.059 38.183 0.879 28.8616
# 12 13.067 38.210 0.872 28.8808
# 13 13.080 38.190 0.992 28.8626
# 14 13.094 38.194 1.102 28.8628
# 15 13.083 38.195 1.144 28.8659
# 16 13.086 38.211 1.060 28.8777
# 17 13.062 38.280 1.025 28.9361
# 18 13.041 38.283 0.986 28.9428
# 19 13.030 38.274 1.030 28.9381
# 20 13.024 38.262 1.092 28.9301
# 21 13.019 38.257 1.140 28.9272
# 22 13.007 38.284 1.235 28.9507
# 23 12.999 38.285 1.324 28.9531
# 24 12.965 38.283 1.392 28.9586
# 25 12.946 38.258 1.459 28.9432
# 26 12.917 38.191 1.489 28.8973
# 27 12.905 38.175 1.591 28.8873
# 28 12.905 38.171 1.633 28.8842
# 29 12.890 38.221 1.653 28.9261
# 30 12.908 38.226 1.672 28.9262
# 31 12.887 38.237 1.584 28.9391
# 32 12.826 38.239 1.575 28.9532
# 33 12.816 38.248 1.599 28.9623
# 34 12.856 38.269 1.573 28.9703
# 35 12.885 38.280 1.505 28.9728
# 36 12.868 38.283 1.552 28.9787
# 37 12.846 38.290 1.503 28.9886
# 38 12.879 38.301 1.444 28.9904
# 39 12.924 38.314 1.381 28.9911
# 40 12.935 38.330 1.316 29.0012
# 41 12.917 38.354 1.284 29.0236
# 42 13.010 38.384 0.973 29.0275
# 43 12.987 38.406 0.730 29.0494
# 44 13.006 38.397 0.724 29.0384
# 45 13.085 38.405 0.784 29.0282
# 46 13.135 38.417 1.013 29.0270
# 47 13.077 38.416 1.045 29.0384
# 48 12.958 38.361 1.450 29.0205
# 49 12.919 38.353 1.693 29.0224
# 50 12.930 38.367 1.572 29.0310
# 51 12.993 38.372 1.477 29.0218
# 52 13.028 38.389 1.309 29.0276
# 53 13.032 38.396 1.211 29.0322
# 54 13.056 38.399 1.119 29.0296
# 55 13.042 38.403 1.031 29.0356
# 56 13.027 38.402 1.022 29.0379
# 57 13.051 38.411 1.062 29.0399
# 58 13.095 38.422 1.063 29.0392
# 59 13.154 38.441 0.975 29.0416
# 60 13.088 38.448 0.911 29.0609
# 61 13.030 38.409 0.959 29.0427
# 62 13.040 38.394 0.990 29.0290
# 63 13.072 38.394 0.998 29.0224
# 64 13.091 38.397 1.010 29.0207
# 65 13.104 38.422 0.956 29.0374
# 66 13.061 38.418 0.964 29.0432
# 67 13.062 38.412 0.993 29.0384
# 68 13.025 38.409 1.064 29.0438plot(marphy_ts,
main = "Masses d'eaux entre Nice et la Corse",
xlab = "Transect Nice - Calvi (stations)")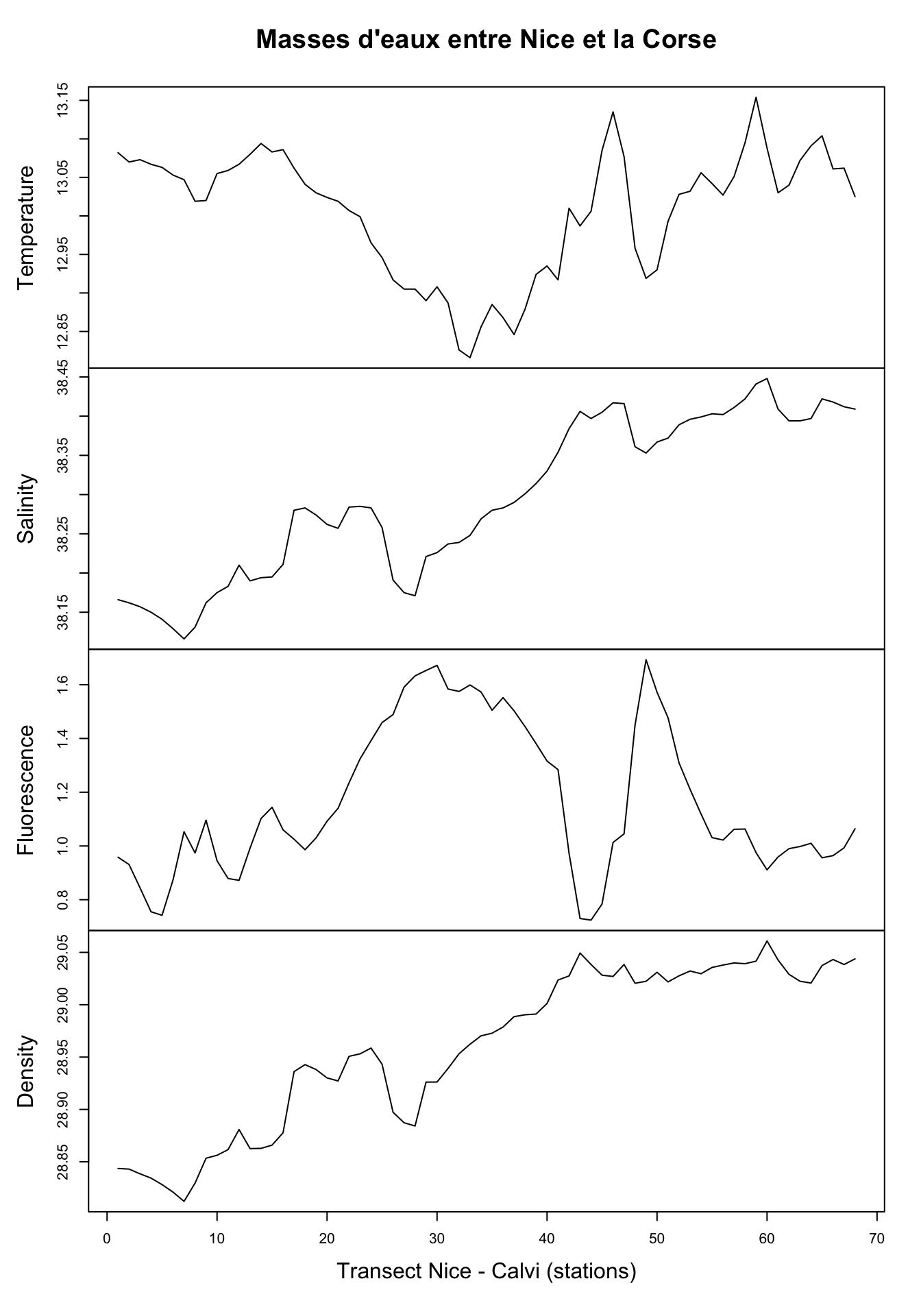
Ici, nous avons quatre variables enregistrées : la température (°C), la salinité de l’eau, la fluorescence (de la chlorophylle) qui est une mesure indirecte du contenu en phytoplancton dont l’abondance dépend elle-même du contenu en sels nutritifs (azote, phosphore, silice), et enfin la densité de l’eau en g/L. Nous observons ici des variations importantes et parfois assez abruptes. En fait, le transect croise un front constitué par une remontée d’eaux profondes, froides et riches en nutriments en plein milieu. De même, marbio est un data table que nous nous empressons de convertir avec ts(), mais ici nous choisissons trois séries parmi l’ensemble des 24 séries pour la représentation graphique à l’aide de l’opérateur [,] :
read("marbio", package = "pastecs") %>.%
ts(.) %->%
marbio_ts
colnames(marbio_ts) # Nom des différentes séries dans le jeu de données multivarié# [1] "Acartia" "AdultsOfCalanus" "Copepodits1"
# [4] "Copepodits2" "Copepodits3" "Copepodits4"
# [7] "Copepodits5" "ClausocalanusA" "ClausocalanusB"
# [10] "ClausocalanusC" "AdultsOfCentropages" "JuvenilesOfCentropages"
# [13] "Nauplii" "Oithona" "Acanthaires"
# [16] "Cladocerans" "EchinodermsLarvae" "DecapodsLarvae"
# [19] "GasteropodsLarvae" "EggsOfCrustaceans" "Ostracods"
# [22] "Pteropods" "Siphonophores" "BellsOfCalycophores"plot(marbio_ts[, c("Acartia", "ClausocalanusA", "Pteropods")],
main = "Plancton entre Nice et la Corse",
xlab = "Transect Nice - Calvi (stations)")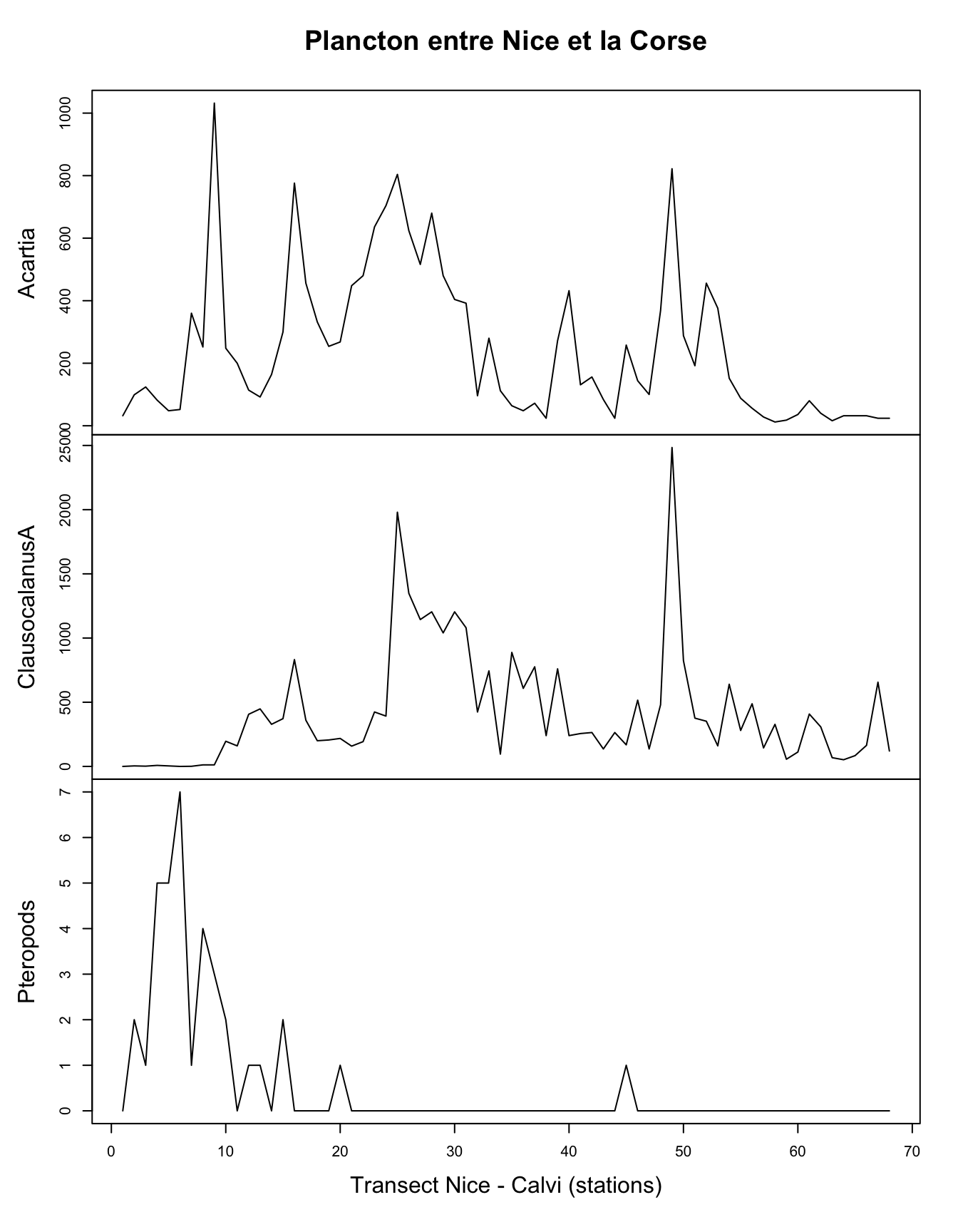
Ici aussi la distribution du plancton le long du transect n’est pas homogène. Alors que les ptéropodes (mollusques planctoniques) se retrouvent essentiellement près de Nice, les crustacés copépodes comme Acartia spp ou Clausocalanus spp se retrouvent plutôt en pleine mer.
Notez que l’on obtient un objet tbl_ts, soit un data frame de type tibble spécial qui reconnait la variable temporelle (on l’appelle aussi un tsibble comme vous pouvez le constater en imprimant l’objet).↩︎