3.3 Machine à vecteurs supports
Les machines à vecteurs supports (Support Vector Machine en anglais, ou SVM en abrégé) forment une autre famille d’algorithmes utilisables en classification supervisée. Au départ, l’idée est simple : il s’agit de déterminer le meilleur hyperplan qui divise l’hyperespace représenté par les attributs décrivant un cas à deux classes. Avec deux attributs seulement (cas le plus simple, disons x1 et x2), cela signifie que nous recherchons une droite qui divise notre plan x1-x2 en deux, chaque région issue de cette séparation représentant le domaine de l’une des deux classes.
Jusqu’ici, l’idée nous semble assez similaire à l’ADL. La grosse différence, c’est que dans l’ADL nous utilisons toutes les données pour définir la position de la frontière, alors que dans SVM, nous n’utilisons que les individus au niveau de la frontière qui forment les fameux “vecteurs supports” à l’origine du nom de la technique. Ces vecteurs supports définissent une marge autour de la frontière. Cette dernière est positionnée de telle façon que la marge en question soit la plus large possible. En d’autres termes, nous cherchons à définir un “no-man’s land”, un fossé le plus large possible autour de la frontière tracée entre les deux classes. Cette approche s’avère judicieuse et performante en pratique.
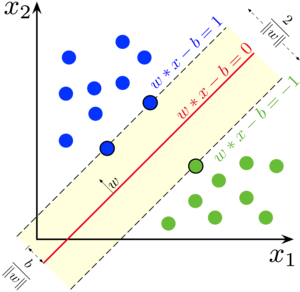
Bon, il nous reste à contourner deux limitations pour que la méthode soit utilisable dans des situations plus générales :
- La frontière entre les deux classes n’est pas forcément linéaire, et en pratique, la plupart du temps elle ne le sera pas.
- Comment généraliser à une situation à plus de deux classes ?
Abordons ces deux points successivement ci-dessous.
3.3.1 Approche par noyau
Le problème de frontière non linéaire se résout par une transformation de l’hyperespace initial vers une version déformée habilement par projection. Si la fonction qui effectue la déformation est correctement choisie, une frontière non linéaire peut être linéarisée, un peu comme une transformation bien choisie des données pour un nuage de points peut éventuellement le linéariser (nous avons abondamment utilisé cette astuce en modélisation).
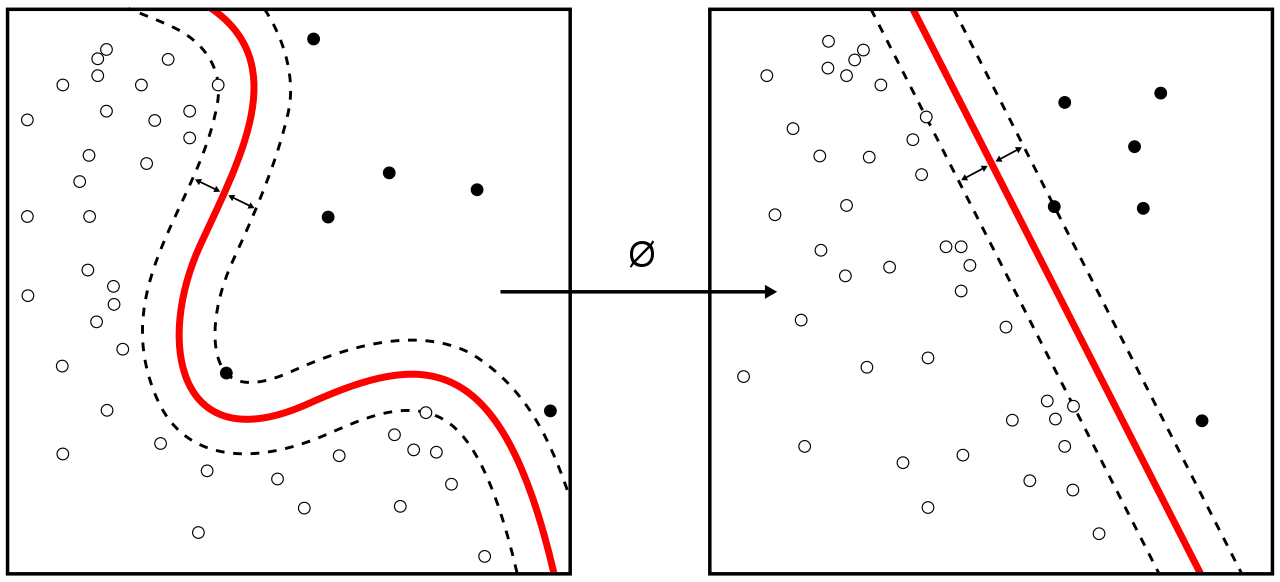
La transformation appliquée est une fonction mathématique appelée noyau (kernel en anglais). Un certain nombre de noyaux ont été définis pour transformer des frontières de forme précise. Par exemple, si la frontière initiale est circulaire, un noyau existe pour linéariser cette frontière en transformant notre plan en hyperbole tridimensionnelle en calculant une troisième dimension telle que x3 = x12 + x22. Découper notre hyperbole 3D par une frontière plane revient alors à découper notre plan initial à l’aide d’une frontière circulaire. Ceci est illustré dans la vidéo suivante.
À retenir
Avec SVM, le choix du noyau et de ses paramètres est une étape cruciale pour obtenir de bons résultats. Il se peut que vous ayez à essayer différents noyaux et différents paramètres de manière itérative avant d’arriver à un résultat satisfaisant. Par contre, une fois le noyau correctement défini, la technique s’avère très puissante.
3.3.2 SVM multiclasses
Bien qu’il ne semble pas évident au premier abord que SVM ne soit défini que pour un cas à deux classes seulement, c’est ainsi que les mathématiciens l’ont développée. Par contre, cette limitation peut être dépassée par une astuce simple : ramener les situations multiclasses à des cas à deux classes. Nous avons déjà observé, en effet, pour la matrice de confusion que nous pouvons toujours réduire un problème multiclasses à deux classes seulement dès lors que nous choisissons une classe cible. Nous calculons ensuite cette classe cible versus tout ce qui n’est pas de cette classe-là. Cette approche est dite “macro”, par contraste avec l’approche “micro” ou les classes sont confrontées individuellement deux à deux.
À vous de jouer !
Par exemple pour trois classes A, B, et C, dans l’approche “macro” nous comparerons A avec B + C en un classifieur unique pour décider si l’item appartient à A ou non. Dans l’approche “micro”, nous comparerons A avec B d’un côté, puis A avec C d’un autre côté (deux classifieurs différents). Nous établirons ensuite un consensus entre ces deux classifieurs pour décider si l’item appartient à la classe A ou non. Ensuite dans les deux approches, nous faisons de même en ciblant cette fois-ci la classe B, et puis finalement la classe C. En rassemblant tous les résultats et en comparant les probabilités d’appartenance aux différentes classes renvoyées par les classifieurs individuels binaires, nous obtenons finalement un classifieur global multiclasse. C’est ainsi que SVM multiclasse fonctionne.
La décomposition d’un classifieur multiclasses en une série de classifieurs binaire par approche “macro” ou “micro” est utile en SVM. Elle l’est aussi pour établir des métriques de performance globales sur base de métriques qui ne se calculent normalement qu’avec deux classes. Nous l’avons déjà abordé dans le module précédent.
Par exemple, dans le cas du score F, nous pouvons calculer un score F global pour l’ensemble d’un classifieur multiclasses en moyennant les scores F de chaque classe. Par contre, comme deux approches co-existent, nous avons donc deux versions : le score F “micro” et le score F “macro”. Le premier déterminera une balance entre les comparaisons deux à deux (un comparé à un) de toutes les classes, tandis que le second envisagera le problème de manière plus globale (un comparé à tous). Les deux points de vue se complètent plus qu’ils ne s’opposent.
Les scores F “micro” et “macro” sont des métriques globales plus utiles que le taux global de reconnaissance (TGR) car ils tiennent compte des performances pour toutes les classes là ou le TGR ne quantifie la situation que de manière générale, délaissant ainsi la classification réalisée pour les classes les plus rares au bénéfice des classes abondantes. Pour faire un parallèle avec la régression, le R2 est un critère utile pour définir l’ajustement d’une droite, mais le critère d’Akaiké sera plus efficace pour définir le meilleur modèle. En classification, c’est pareil : le TGR quantifie les performances globales, mais les scores F micro et macro sont des biens meilleurs critères pour choisir son classifieur optimal.
Les scores F micro et macro sont calculés sur nos objets confusion et renvoyés parsummary(). Prenez donc la bonne habitude de les utiliser comme critères globaux de performance de vos classifieurs multiclasses de préférence au TGR ou au taux d’erreur globale.
3.3.3 SVM et Pima
Voyons maintenant ce que donne un classifieur SVM sur notre jeu de données pima1. Une version de SVM étant disponible dans {mlearning}, nous pouvons appliquer cet algorithme facilement avec un code R qui nous est à présent familier (nous choisissons ici la validation croisée dix fois pour en quantifier les performances).
set.seed(3674)
pima1_svm <- mlSvm(data = pima1, diabetes ~ .)
pima1_svm_conf <- confusion(cvpredict(pima1_svm, cv.k = 10), pima1$diabetes)
plot(pima1_svm_conf)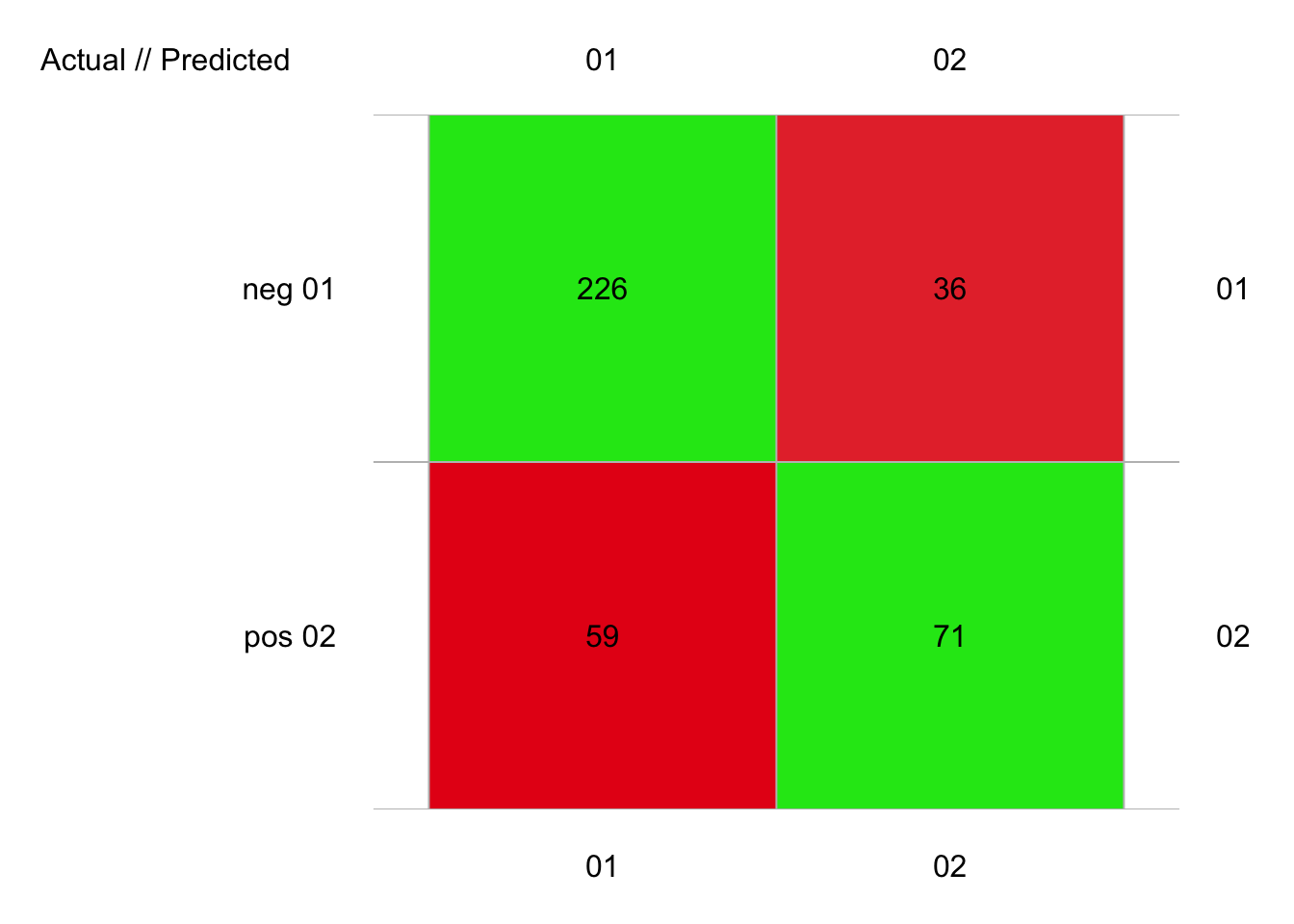
# 392 items classified with 297 true positives (error = 24.2%)
#
# Global statistics on reweighted data:
# Error rate: 24.2%, F(micro-average): 0.716, F(macro-average): 0.713
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8263254 0.8625954 0.7929825 0.5461538 0.6635514 0.4538462 0.1374046
# pos 0.5991561 0.5461538 0.6635514 0.8625954 0.7929825 0.1374046 0.4538462
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.2070175 0.3364486 1.900634 0.2515859 2.356920 0.3119842 0.7043746
# pos 0.3364486 0.2070175 3.974786 0.5261402 3.205291 0.4242825 0.7043746
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.4319813 73.15029 0.02933673 285 262 23 226 59 36 71
# pos 0.4319813 73.15029 0.02933673 107 130 -23 71 36 59 226Ici, avec tous les arguments par défaut de mlSvm() nous avons un taux d’erreur de 24%, mais plus important, des F micro et macro d’environ 0.71. Si nous comparons à notre classifieur forêt aléatoire sur les mêmes données, nous avions 21% d’erreur et F micro ou macro de 0.75. Donc, notre SVM non optimisé fait moins bien que la forêt aléatoire… mais le travail n’est pas terminé. Le noyau par défaut (kernel =) est radial. Les autres options (voir ?e1071::svm) sont linear pour aucune transformation, polynomial (dans ce cas, préciser aussi degree et coef0, 3 et 0 respectivement par défaut) pour une frontière plus générale et sigmoid (préciser coef0, 0 par défaut).
Un noyau linéaire fait mieux que le noyau radial :
set.seed(857)
pima1_svm2 <- mlSvm(data = pima1, diabetes ~ ., kernel = "linear")
pima1_svm2_conf <- confusion(cvpredict(pima1_svm2, cv.k = 10), pima1$diabetes)
plot(pima1_svm2_conf)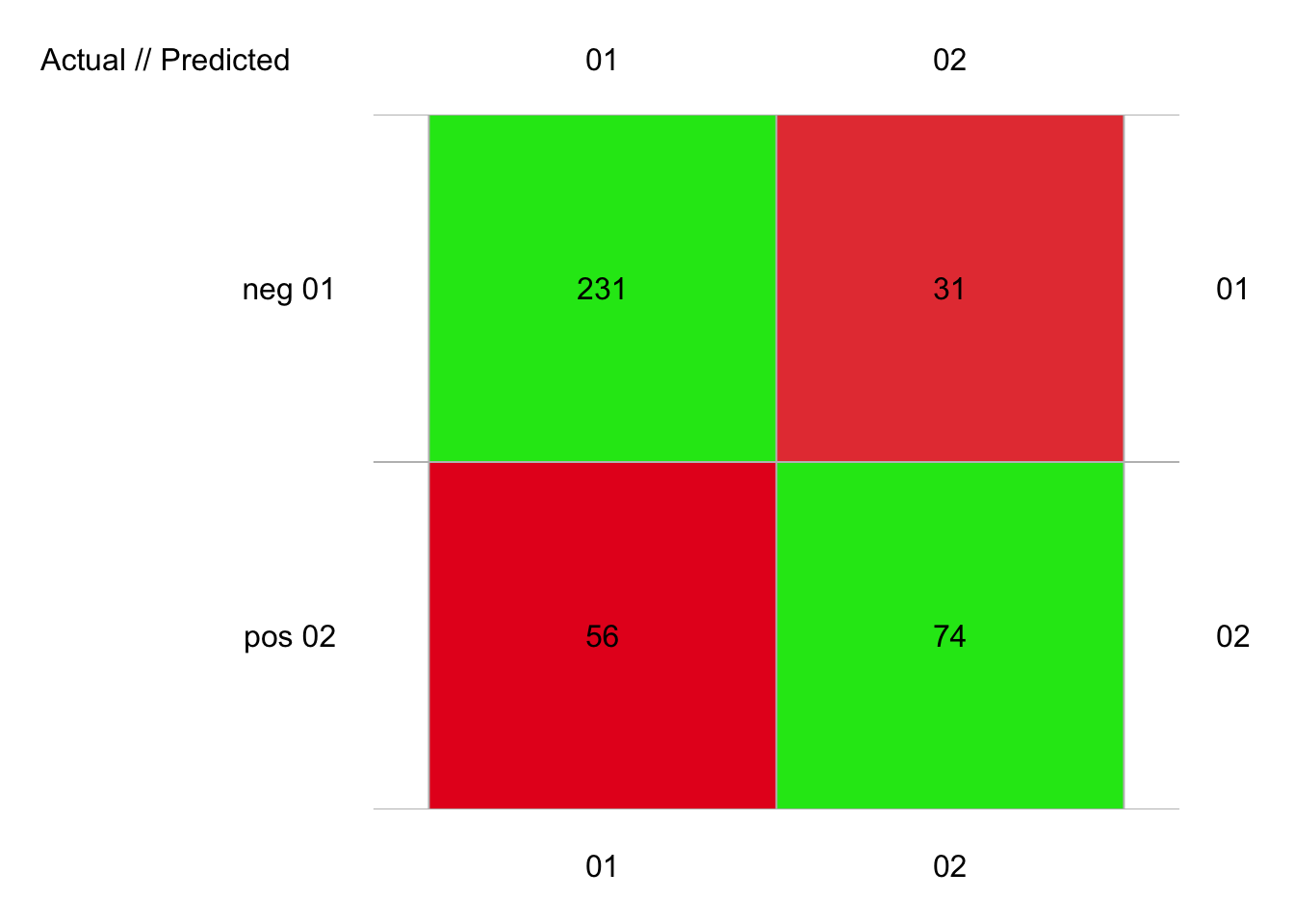
# 392 items classified with 305 true positives (error = 22.2%)
#
# Global statistics on reweighted data:
# Error rate: 22.2%, F(micro-average): 0.74, F(macro-average): 0.736
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8415301 0.8816794 0.8048780 0.5692308 0.7047619 0.4307692 0.1183206
# pos 0.6297872 0.5692308 0.7047619 0.8816794 0.8048780 0.1183206 0.4307692
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.1951220 0.2952381 2.046756 0.2078605 2.726200 0.2768622 0.7254551
# pos 0.2952381 0.1951220 4.810918 0.4885781 3.611905 0.3668110 0.7254551
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.4793765 90.08232 0.03188776 287 262 25 231 56 31 74
# pos 0.4793765 90.08232 0.03188776 105 130 -25 74 31 56 231On se rapproche des scores de la forêt aléatoire ici avec un F micro de 0.74 et un F macro de 0.736. Le noyau sigmoïde est ici désastreux, mais le noyau polynomial de degré 2 et avec un coef0 = 1 donne ceci :
set.seed(150)
pima1_svm3 <- mlSvm(data = pima1, diabetes ~ ., kernel = "polynomial",
degree = 2, coef0 = 1)
pima1_svm3_conf <- confusion(cvpredict(pima1_svm3, cv.k = 10), pima1$diabetes)
plot(pima1_svm3_conf)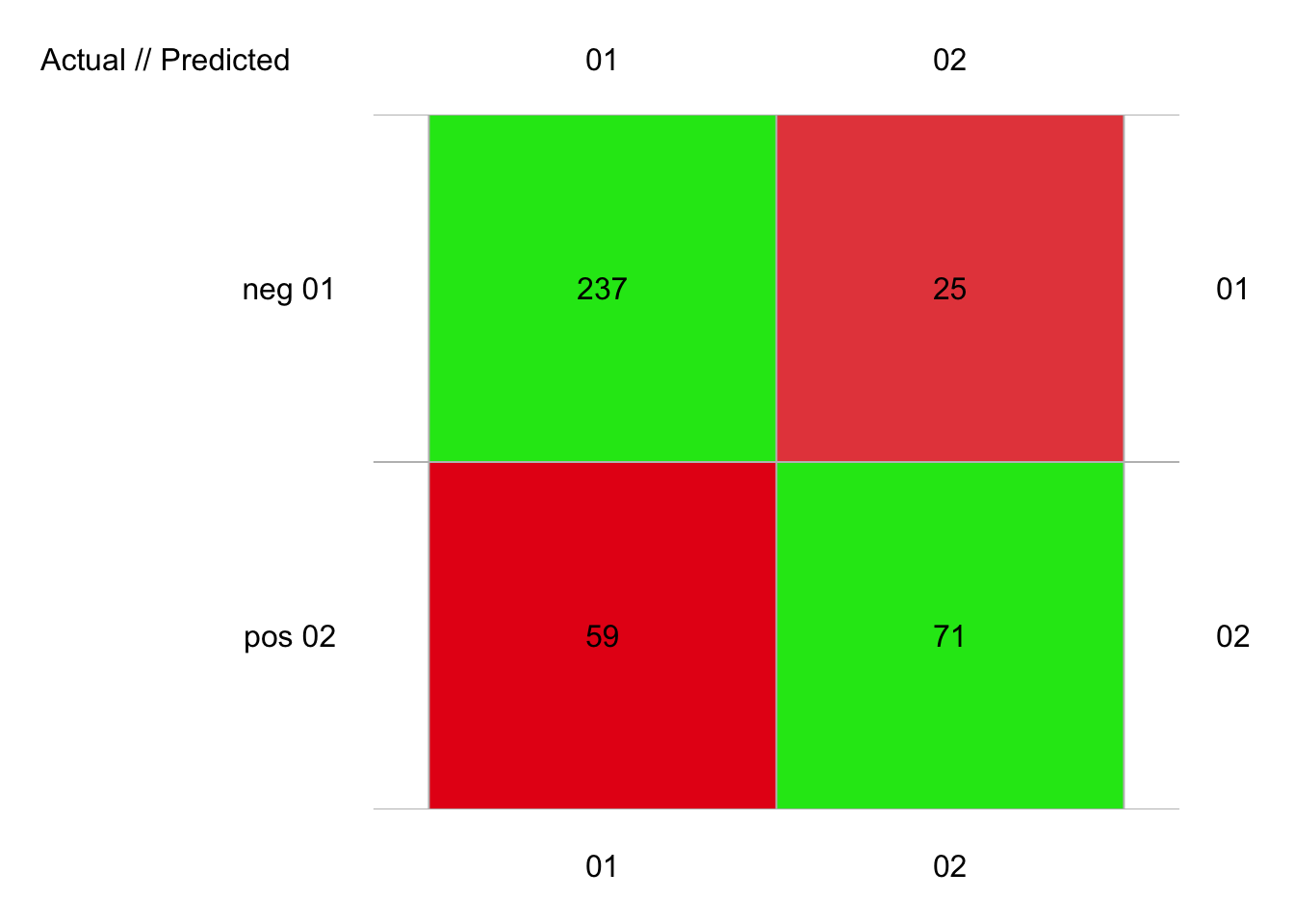
# 392 items classified with 308 true positives (error = 21.4%)
#
# Global statistics on reweighted data:
# Error rate: 21.4%, F(micro-average): 0.747, F(macro-average): 0.739
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8494624 0.9045802 0.8006757 0.5461538 0.7395833 0.45384615 0.09541985
# pos 0.6283186 0.5461538 0.7395833 0.9045802 0.8006757 0.09541985 0.45384615
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.1993243 0.2604167 1.993143 0.1747124 3.074595 0.2695089 0.725367
# pos 0.2604167 0.1993243 5.723692 0.5017202 3.710452 0.3252461 0.725367
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.4934705 95.45714 0.04336735 296 262 34 237 59 25 71
# pos 0.4934705 95.45714 0.04336735 96 130 -34 71 25 59 237Avec un F micro de 0.747 et un F macro de 0.739, nous nous rapprochons très fortement des performances de la forêt aléatoire.
À retenir
L’algorithme SVM est potentiellement très performant, mais il est délicat parce que de nombreux paramètres doivent être optimisés. Nous n’avons discuté que le noyau, mais il y a aussi la mise à l’échelle des variables ou non, la pondération des observations, etc., comme paramètres optimisables.
Pour en savoir plus
Une explication des SVM plus en détails (en français)
Une présentation de SVM en français détaillant un peu plus l’aspect mathématique de SVM.