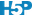2.3 K plus proches voisins

K plus proches voisins (k-nearest neighbours en anglais ou k-NN en abrégé) est certainement la technique la plus intuitive en classification supervisée. Malgré sa simplicité inhérente, elle offre de bonnes prestations. La classification supervisée s’effectue par une analyse de la matrice de distances de Mahalanobis (équivalente à la distance euclidienne ou géométrique appliquée sur des données réduites de variance unitaire) entre un individu d’intérêt à reconnaître et les individus du set d’apprentissage.

La classification par les k plus proches voisins compare un individu inconnu (en gris) avec les individus de classe connue du set d’apprentissage (bleus et rouges matérialisant deux classes différentes) du point de vue de la distance de Mahalanobis. Ici k = 3, et l’individu inconnu est considéré comme bleu puisqu’il est plus proche de deux bleus contre un seul rouge.

En d’autres termes, il s’agit de calculer la distance géométrique qui sépare un individu d’intérêt de tous les individus du set d’apprentissage dans un espace réduit, c’est-à-dire, un espace où chaque variable est mise à l’échelle de telle manière que sa variance soit unitaire. La classe attribuée à l’individu d’intérêt sera la même que celle du, ou des k individus les plus proches (d’où le nom de la méthode). Des variantes utilisent naturellement d’autres calculs de distances : euclidiennes, manhattan, etc.

Un seul paramètre doit donc être défini : k, représentant le nombre d’individus proches considérés. Un vote à la majorité permet de déterminer à quel groupe appartient l’objet testé. En cas d’ex æquo, la classe de l’individu du set d’apprentissage le plus proche est utilisée. Pour minimiser le risque d’ex æquo, k est généralement choisi impair. Dans notre schéma, nous utilisons k = 3, valeur qui s’est avérée optimale dans beaucoup de situations. La recherche de la valeur optimale de k dans le cadre de l’application finale sera évidemment possible ultérieurement.

À vous de jouer !

2.3.1 Pima avec k-NN

La méthode des k plus proches voisins est implémentée dans {mlearning} dans la fonction mlKnn(). En pratique, il suffit de substituer cette fonction dans la logique du code {mlearning}. Un argument est k= qui indique le nombre de k voisins à prendre en compte.

set.seed(3675)
pima1_knn <- mlKnn(data = pima1, diabetes ~ ., k = 3)
pima1_knn_conf <- confusion(cvpredict(pima1_knn, cv.k = 10), pima1$diabetes)
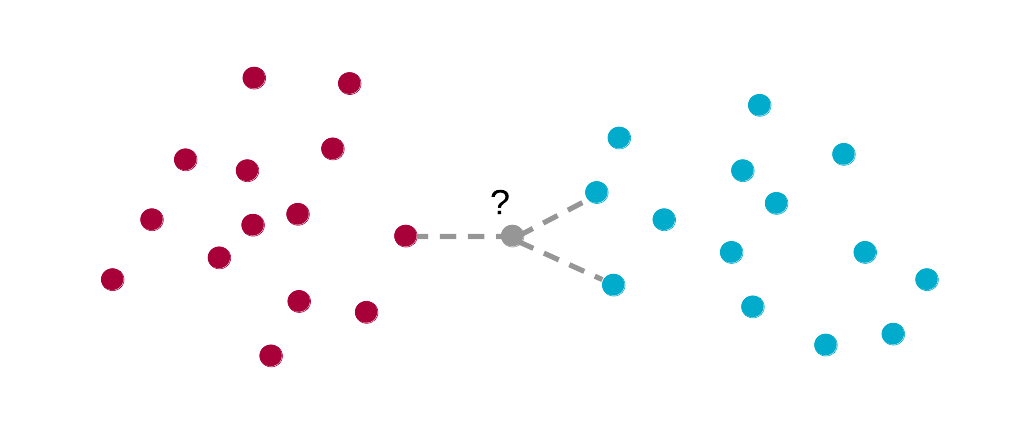
plot(pima1_knn_conf)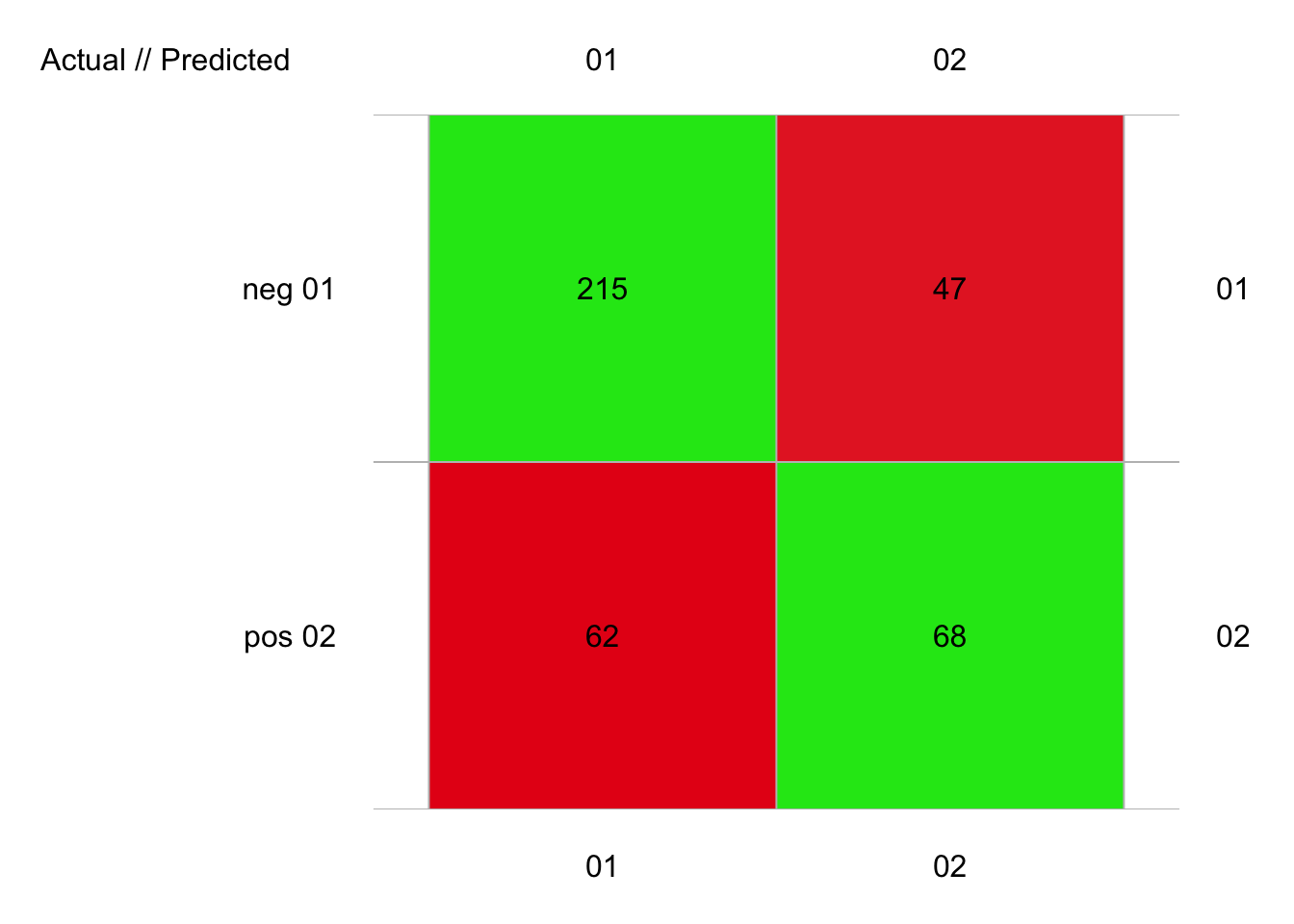

summary(pima1_knn_conf, type = c("Fscore", "Recall", "Precision"))

# 392 items classified with 283 true positives (error = 27.8%)
# 
# Global statistics on reweighted data:
# Error rate: 27.8%, F(micro-average): 0.678, F(macro-average): 0.676
# 
#        Fscore    Recall Precision
# neg 0.7977737 0.8206107 0.7761733
# pos 0.5551020 0.5230769 0.5913043

Ici, nous avons 28% d’erreur, soit plus qu’avec l’ADL. Mais la valeur k = 3 n’est pas le meilleur choix ici. Expérimentez par vous-même pour découvrir combien de plus proches voisins, nous devons considérer pour minimiser l’erreur.

Pour pima2, nous obtenons :

set.seed(127)
pima2_knn <- mlKnn(data = pima2, diabetes ~ ., k = 3)
pima2_knn_conf <- confusion(cvpredict(pima2_knn, cv.k = 10), pima2$diabetes)
plot(pima2_knn_conf)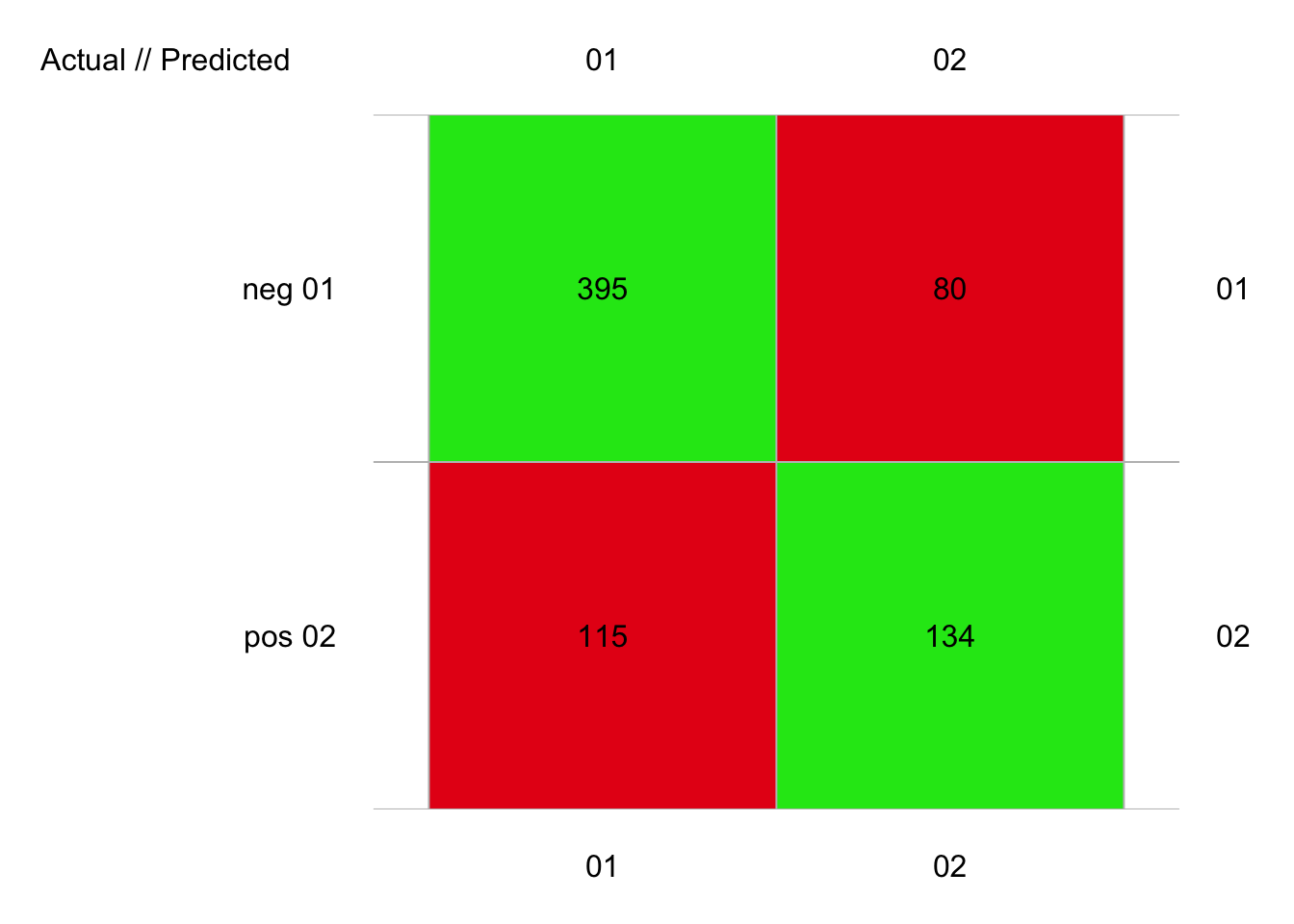

summary(pima2_knn_conf, type = c("Fscore", "Recall", "Precision"))

# 724 items classified with 529 true positives (error = 26.9%)
# 
# Global statistics on reweighted data:
# Error rate: 26.9%, F(micro-average): 0.693, F(macro-average): 0.69
# 
#        Fscore    Recall Precision
# neg 0.8020305 0.8315789 0.7745098
# pos 0.5788337 0.5381526 0.6261682

Avec 27% d’erreur, nous avons un résultat similaire encore une fois, mais toujours légèrement moins bon que l’ADL.