5.1 Décomposition de séries
Toutes les techniques présentées dans cette partie ont pour but de décomposer des séries spatio-temporelles régulières (donc, à pas de temps constant et sans trous) en deux ou plusieurs composantes. On extrait soit une composante issue d’un filtrage ou d’un lissage, ou alors correspondant à un modèle (variation cyclique, tendance linéaire, polynomiale, exponentielle, etc …). Quel que soit le nombre de composantes obtenues, la dernière est toujours le résidu (residuals en anglais), c’est-à-dire, la fraction de la série initiale (series) qui ne se retrouve dans aucune des autres composantes (components) extraites.
Pour un modèle additif, on aura :
series = component1 + component2 + … + residuals
Un tel modèle est également appelé linéaire lorsque chaque composante est une combinaison linéaire de la ou des variables dépendantes, en l’occurrence pour les séries spatio-temporelles, le temps ou l’espace, ou les deux ensemble.
Un modèle multiplicatif se définira selon un schéma équivalent, mais dans ce cas, c’est le produit des composantes qui donnera la série. Une des composantes (la série filtrée, la série désaisonnalisée ou la tendance générale, selon le contexte), est alors exprimée dans les mêmes unités que la série de départ, alors que les autres sont des facteurs multiplicatifs adimensionnels. Il est possible de transformer un modèle multiplicatif en un modèle additif par une transformation logarithmique du signal observé, puisque le logarithme d’un produit est égal à la somme des logarithmes des facteurs. Si l’opération donne une combinaison linéaire des logarithmes des facteurs, on dit que l’on a linéarisé le signal par la transformation logarithmique.
On pourrait encore définir des modèles mixtes où certaines composantes sont multiplicatives alors que d’autres sont additives, mais il n’y a alors plus moyen de les linéariser. Pour cette raison, de tels modèles sont très peu répandus. La nature de la ou des composantes dépend du traitement effectué. Par exemple pour un filtrage, il s’agit de la série filtrée, pour une stationnarisation, il s’agit de la tendance générale extraite, pour une désaisonnalisation, il s’agit du cycle saisonnier, etc.
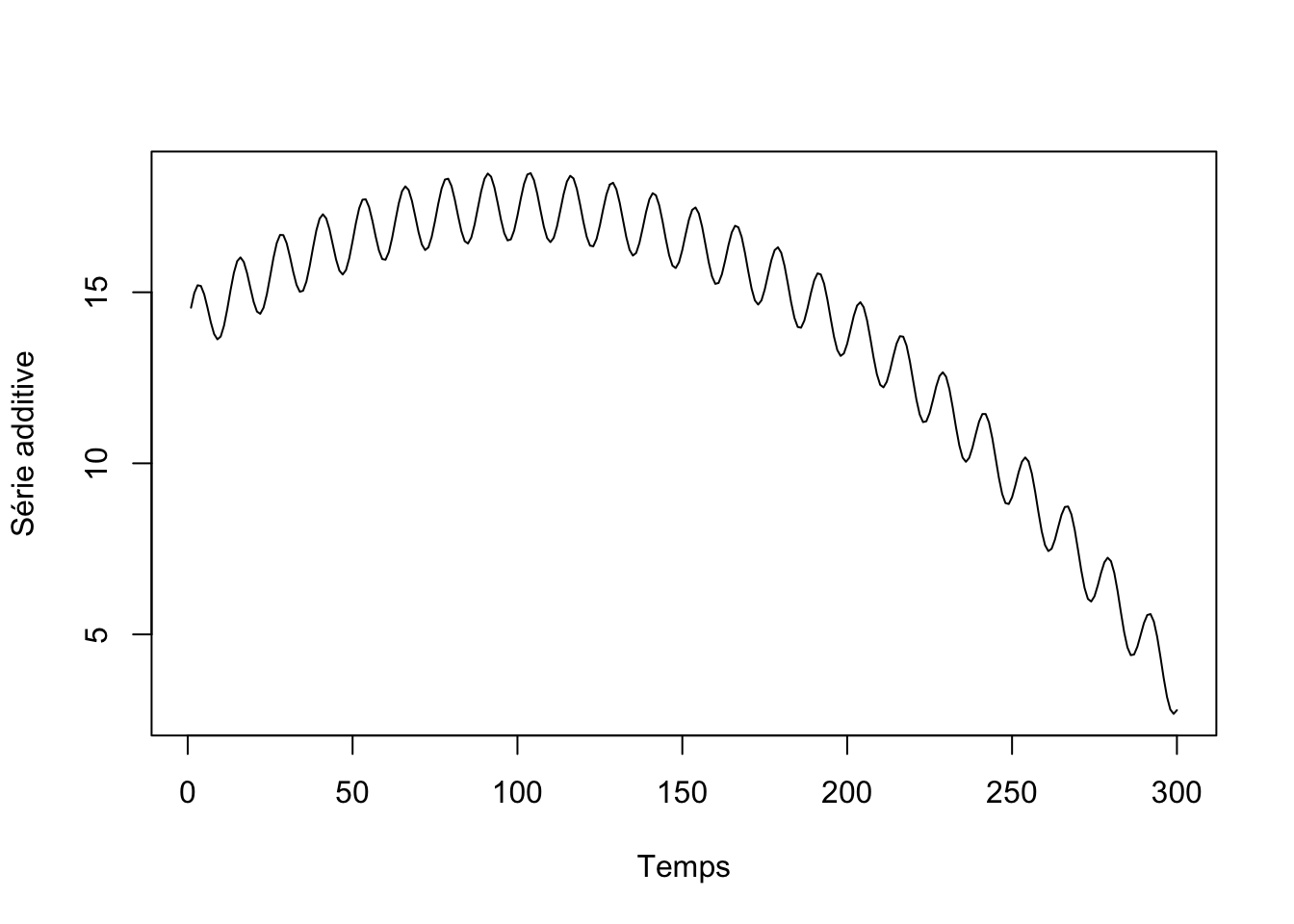
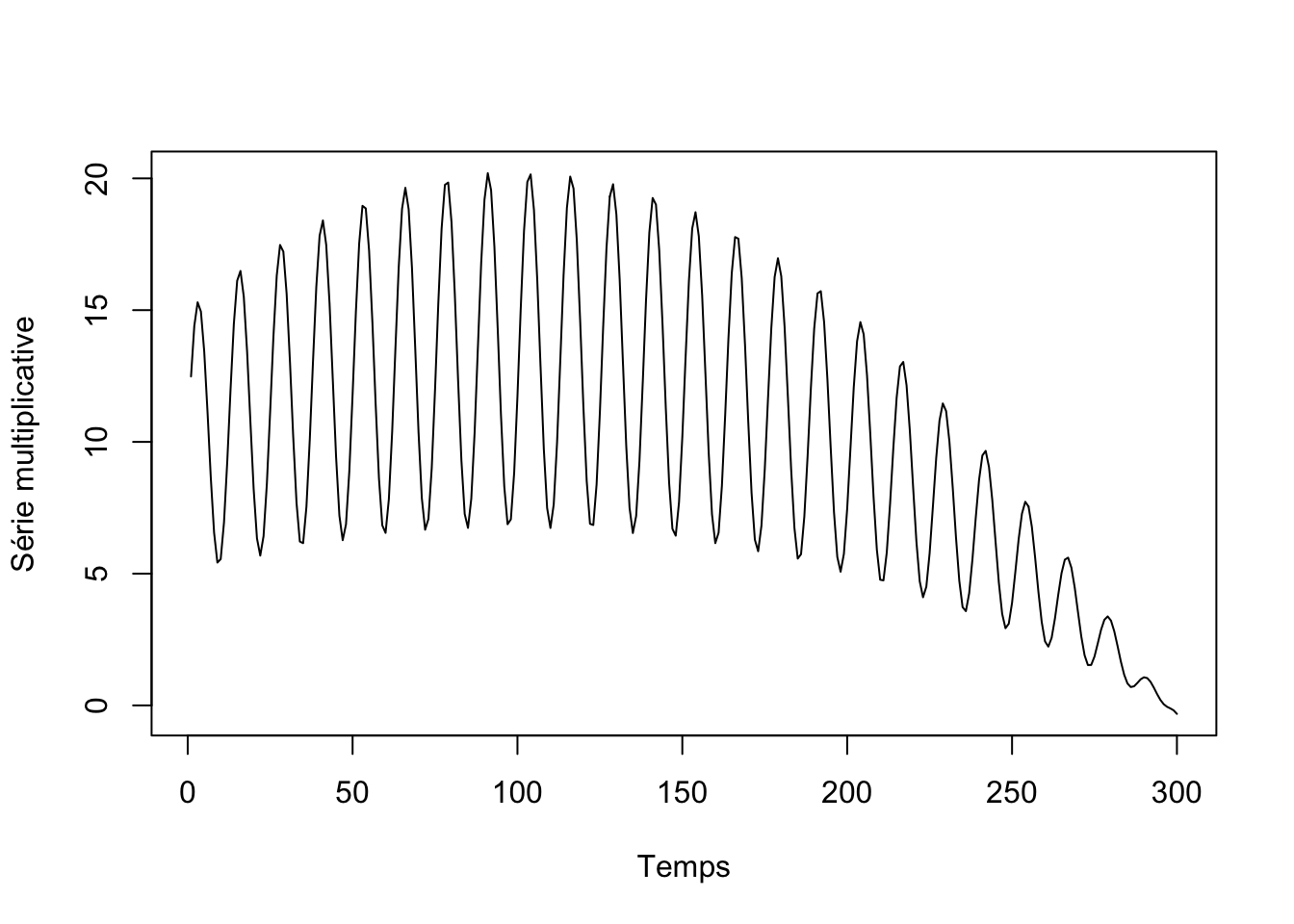
Lorsqu’un cycle et une tendance à long terme sont tous deux présents dans la série, nous pouvons aisément discerner le modèle additif du modèle multiplicatif. En effet, dans le premier cas, l’amplitude du signal cyclique ne varie pas en fonction de la tendance, contrairement au second cas, comme illustré ci-dessous.
5.1.1 Fonction générale de décomposition
Dans {pastecs}, toutes les techniques de décomposition de séries fonctionnent selon le même canevas et renvoient toutes un objet tsd (time series decomposition). Cet objet contient à la fois les composantes de la ou des séries qui ont été décomposées, des informations sur la méthode utilisée, ainsi que des données supplémentaires qui servent au diagnostic du traitement réalisé.
La fonction centrale qui effectue le traitement sur une ou plusieurs séries et renvoie un objet tsd est tsd(). Son argument method= permet de sélectionner une méthode de traitement à appliquer à toutes les séries à décomposer. Son argument type= indique si le modèle est additif ou multiplicatif. Cette fonction appelle d’autres fonctions plus simples decxxx() où xxx est le nom de la méthode (ex. : decmedian() pour la méthode des médianes mobiles, par exemple, que nous étudierons plus loin). Les fonctions decxxx() ne peuvent traiter qu’une série à la fois, et ne sont normalement pas appelées directement par l’utilisateur6.
Une fois qu’une décomposition est réalisée, il est possible d’extraire les différentes composantes (grâce à tseries()) ou une partie d’entre elles (en utilisant la méthode extract()) et de les retransformer en objet de séries régulières (objet ts ou mts). On peut ainsi appliquer de nouvelles méthodes de décomposition sur un ou plusieurs composants et approfondir l’analyse des séries par des traitements de décomposition en cascade jusqu’à ce qu’on ait extrait et analysé toute l’information pertinente contenue dans ces séries.
Exemple
Notre jeu de données co2 est un bon point de départ pour explorer la décomposition d’une série spatio-temporelle.
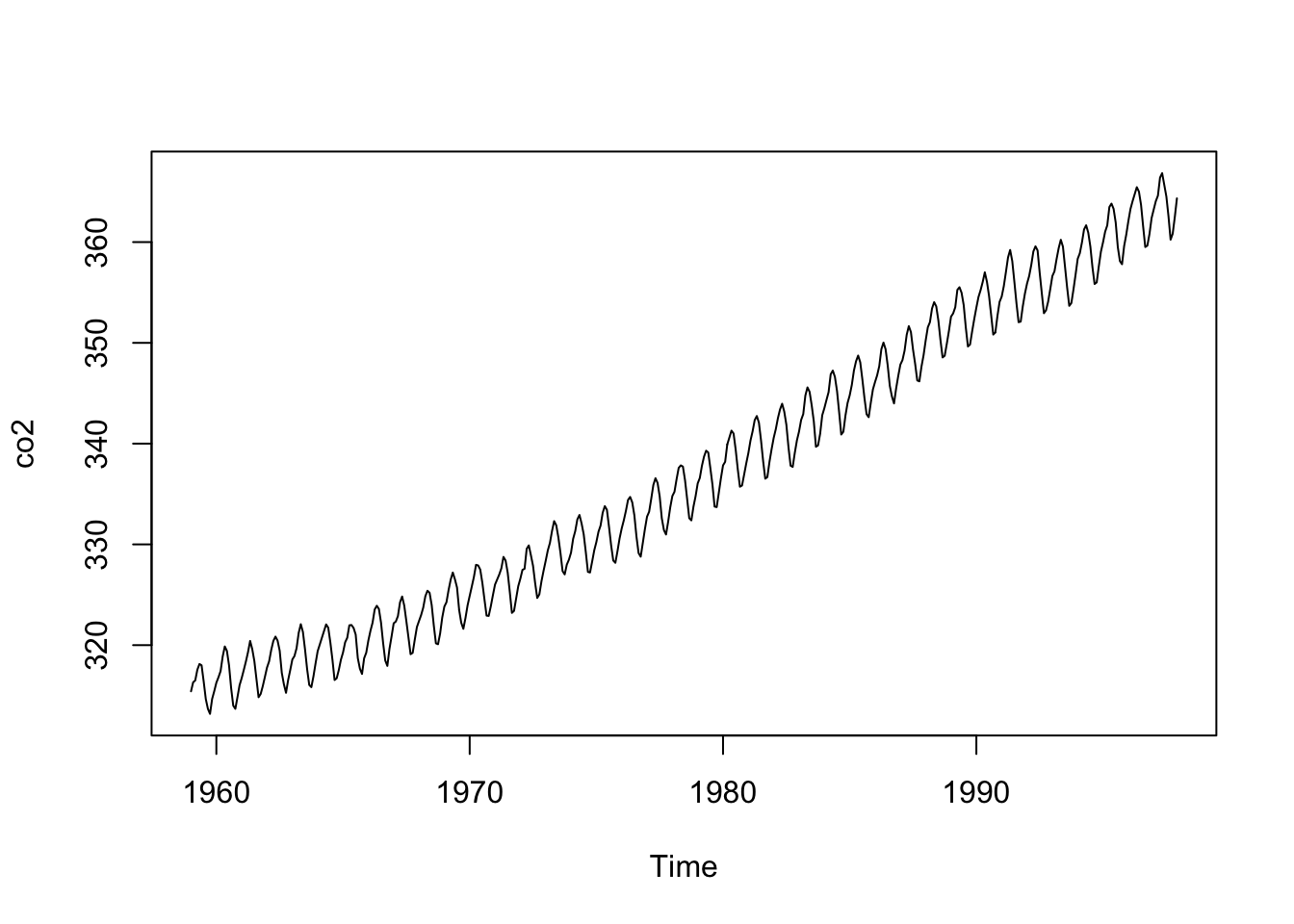
En effet, nous voyons clairement deux composantes présentes : un cycle saisonnier d’une part, et une tendance à l’augmentation sur le long terme, d’autre part. De plus, le modèle est très clairement additif ici, car l’amplitude du cycle ne dépend pas de la valeur atteinte par la tendance générale. Voyons en pratique comment se fait cette décomposition.
Une technique efficace pour lisser une série, et en particulier, en éliminer un cycle est la décomposition par moyennes mobiles. Pour l’instant, concentrez-vous sur la façon d’utiliser ce filtrage et sur ce qui en résulte. Nous aborderons un peu plus loin le détail des techniques employées. Nous utilisons donc tsd(<series>, method = "average", type = "additive", <autres arguments>). N’oubliez pas d’indiquer que vous voulez utiliser les packages liés à l’analyse des séries temporelles avec SciViews::R en lui indiquant "ts".
SciViews::R("ts") # À exécuter une fois en début de document
co2_dec <- tsd(co2, method = "average", type = "additive", order = 6, times = 3)
plot(co2_dec, col = 1:3)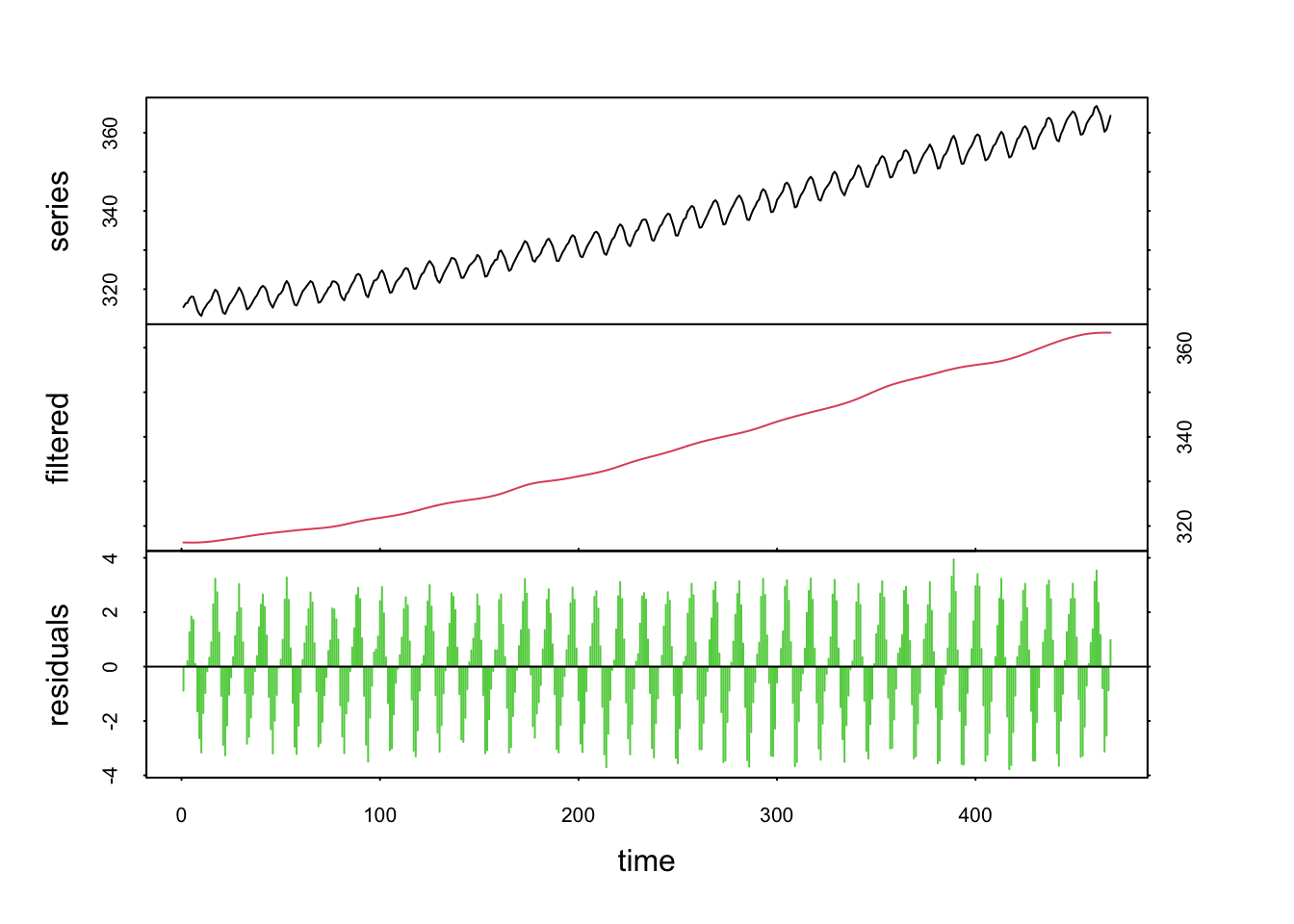
Nous verrons plus loin ce que order= et times= veulent dire. À noter que type = "additive" est la valeur par défaut et peut donc être omise ici. La méthode plot() est ensuite utilisée sur l’objet résultant (ici en utilisant les couleurs de la palette par défaut, 1 = noir, 2 = rouge et 3 = vert pour mettre en évidence les différentes séries). L’axe des abscisses numérote ici les observations par ordre croissant pour les retrouver facilement dans l’objet de départ si nécessaire. En haut sur le graphique, la série de départ en noir, au milieu en rouge, la série filtrée, et en bas en vert, les résidus qui contiennent entre autres le cycle.
L’objet co2_dec est de classe tsd.
# [1] "tsd"Outre son graphique qui est des plus utiles pour juger le résultat de notre décomposition visuellement, nous pouvons retransformer toutes les composantes obtenues en un objet mts à l’aide de tseries() ; ou alors, extraire une ou plusieurs composantes avec extract(). Effectuons les deux successivement.
# [1] "mts" "ts" "matrix"# [1] "filtered" "residuals"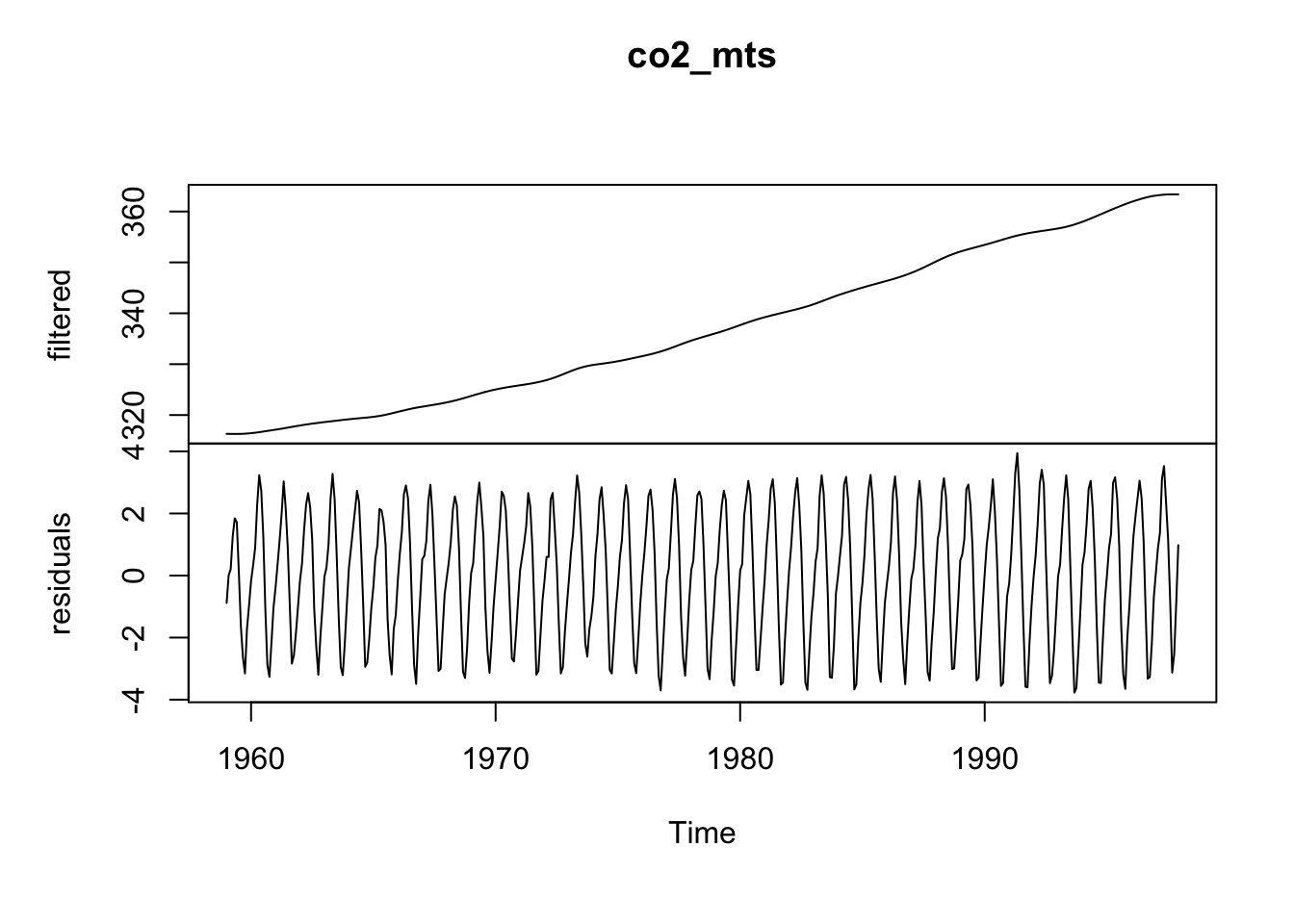
En partant d’un objet ts qui contient une série unique, nous aboutissons donc à un objet mts qui contient deux composantes nommées filtered et residuals après avoir appliqué tsd(method = "average") suivi de tseries(). La composante filtered est essentiellement la tendance à long terme dans le cas présent, tandis que les résidus sont constitués par la série stationnarisée dont la tendance générale est retirée. Nous pouvons parfaitement continuer à travailler avec cet objet mts, et c’est d’ailleurs assez pratique de conserver les deux composantes dans un même objet. Les analyses se font comme d’habitude en sélectionnant la série à traiter à l’aide de l’opérateur [,] :
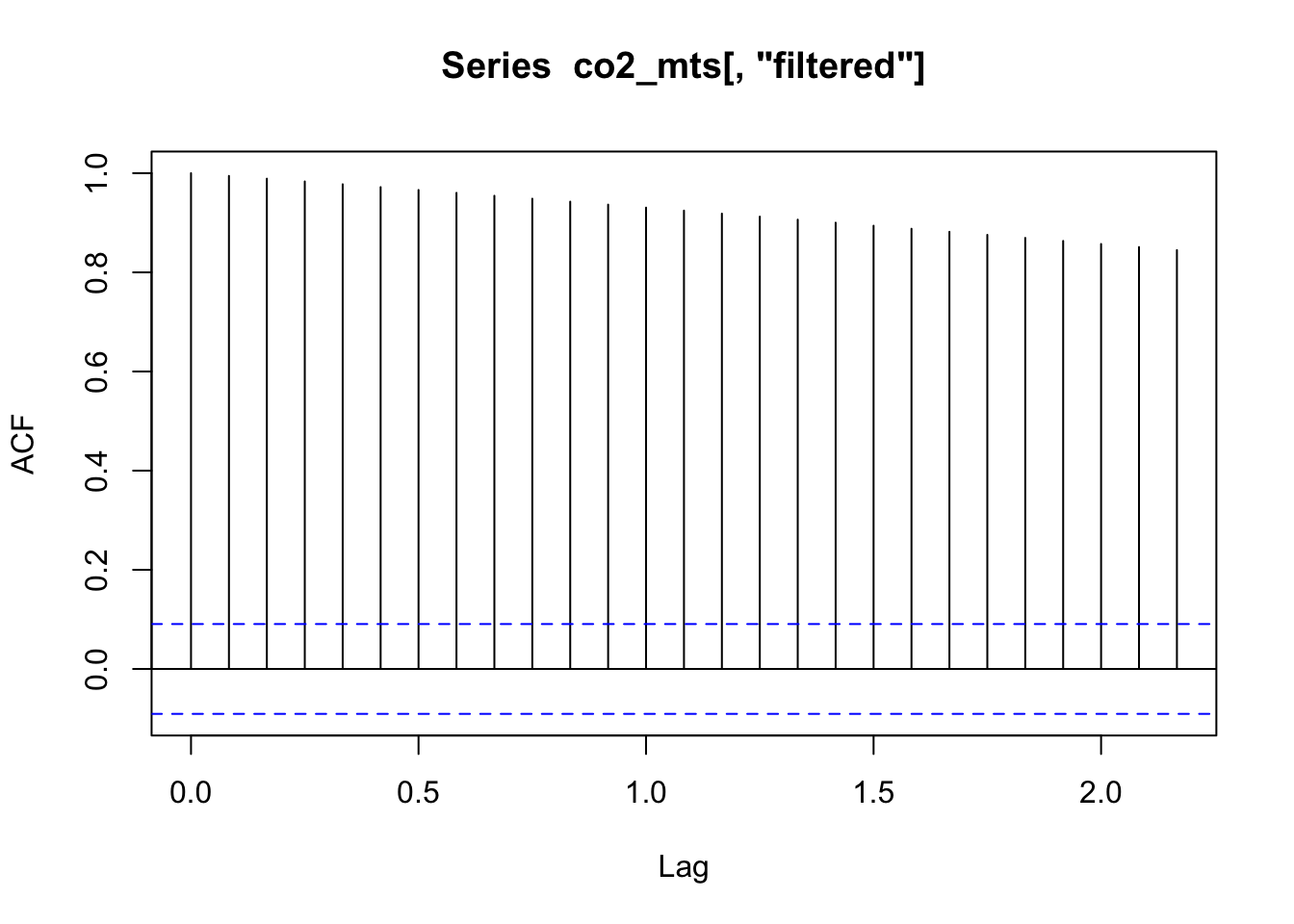
Nous avons ici un parfait exemple de fonction d’autocorrélation pour une tendance pure.
Nous pouvons aussi extraire une ou plusieurs composantes de co2_tsd. Si nous souhaitons extraire la composante résiduelle uniquement sous forme d’un objet ts que nous appellerons co2_stat, nous ferons ceci :
co2_stat <- extract(co2_dec, components = "residuals")
class(co2_stat) # C'est bien une série univariée# [1] "ts"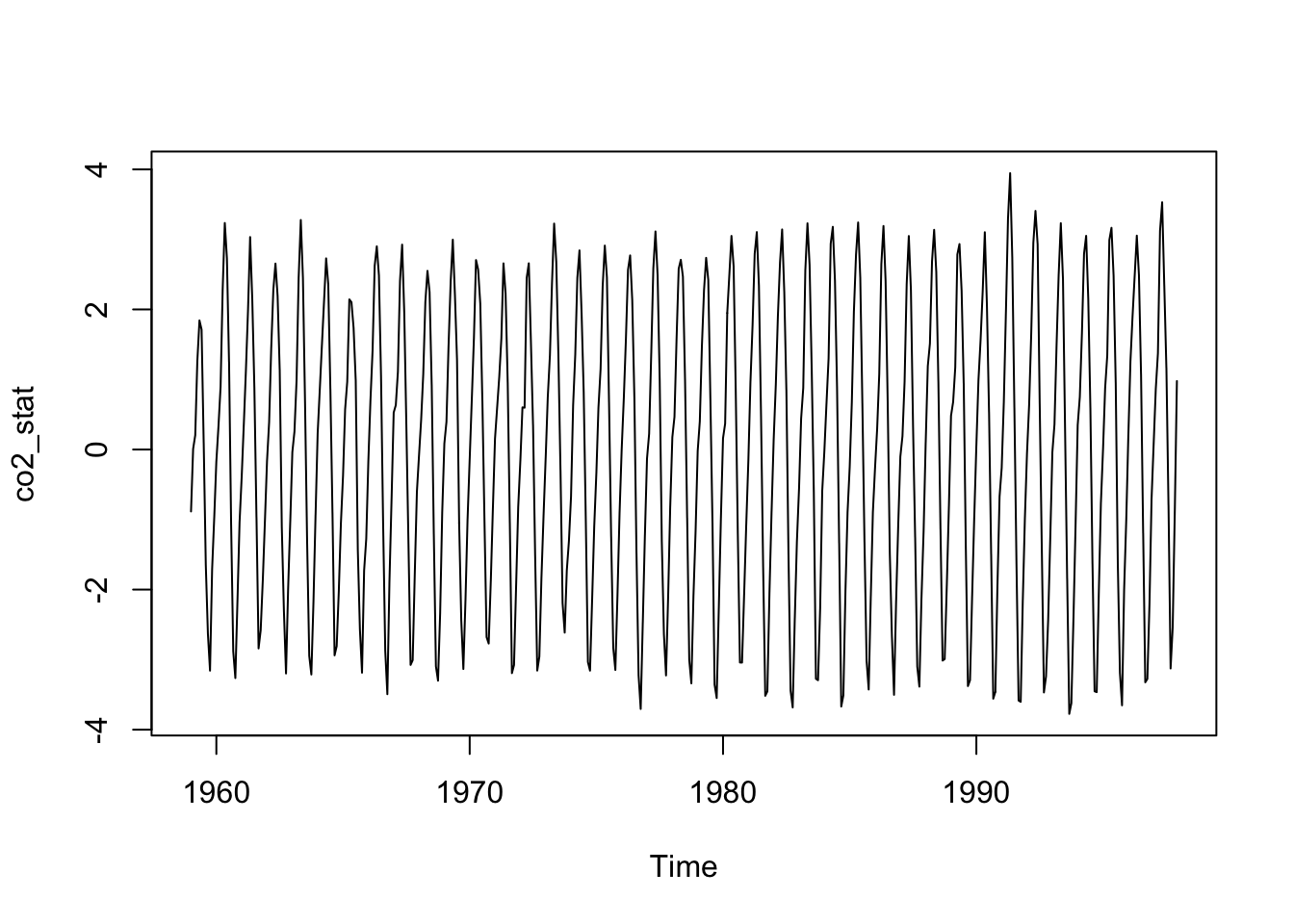
Comme co2_stat est maintenant une série stationnarisée, nous pouvons réaliser une analyse spectrale dessus.
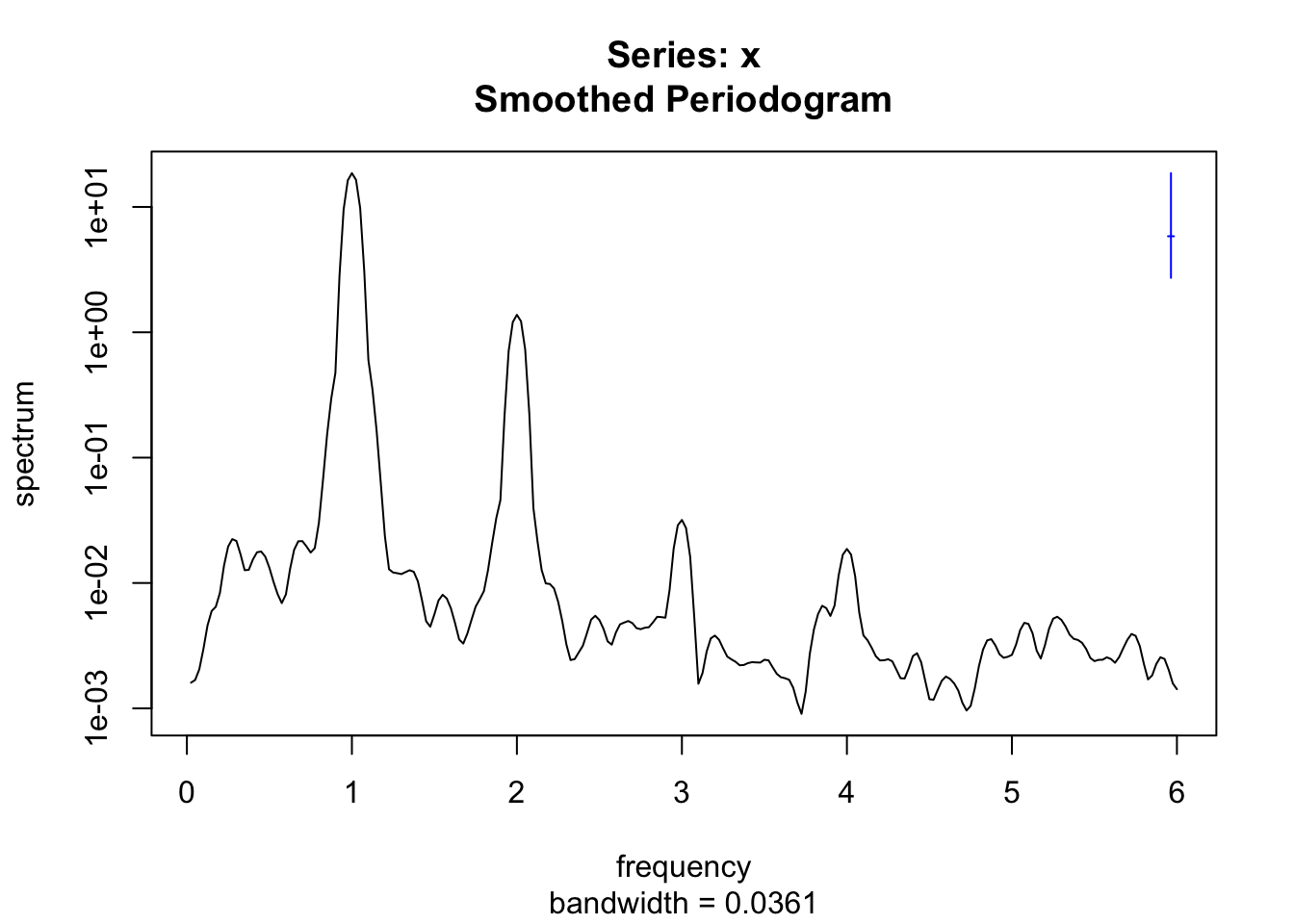
Nous avons un cycle saisonnier très net, et un second pic, mais tout juste pas significatif. Rien n’interdit de décomposer encore plus avant notre série, par exemple, en déterminant comment la composante saisonnière peut être ajustée ou non avec un signal sinusoïdal parfait (encore une fois, les détails de la technique seront abordés plus loin). Il nous suffit de construire un modèle sinusoïdal qui s’ajuste dans les données et d’utiliser ensuite tsd(<series>, method = "reg", xreg = predict(<model>)) pour effectuer la décomposition de la série à l’aide de ce modèle (nous utilisons une astuce pour ajuster ce modèle sinusoïdal à l’aide de lm() que nous expliquerons, encore une fois, plus loin).
t <- time(co2_stat) # t est la variable indépendante du modèle
co2_lm <- lm(co2_stat ~ I(cos(2*pi*t)) + I(sin(2*pi*t))) # Notez que data= n'est pas utilisé ici
plot(t, predict(co2_lm), type = "l")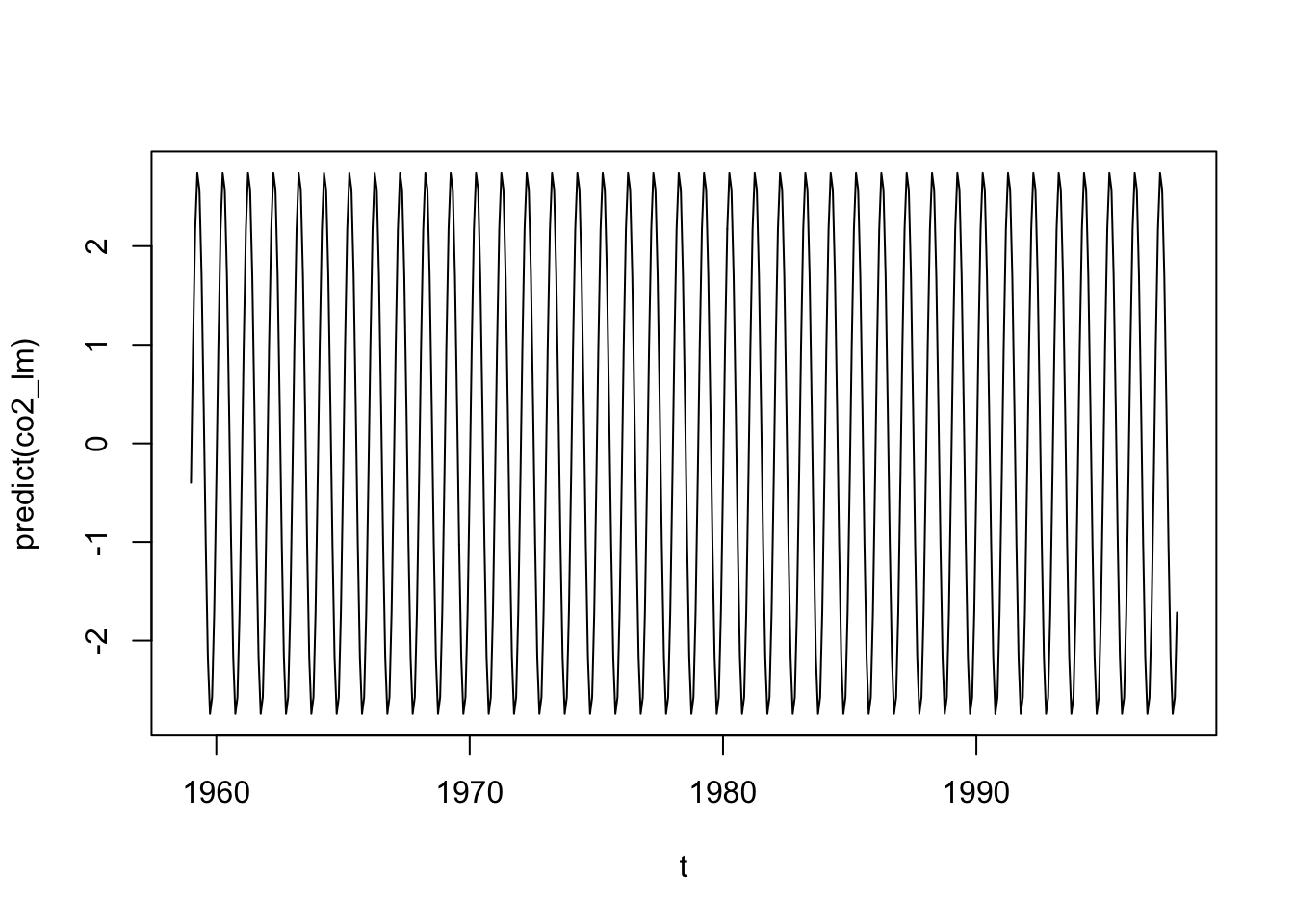
L’objet co2_lm contient notre modèle. Sa méthode predict() permet de déterminer les valeurs de CO2 prédites par ce modèle, et c’est ces valeurs que nous utilisons ensuite pour notre décomposition :
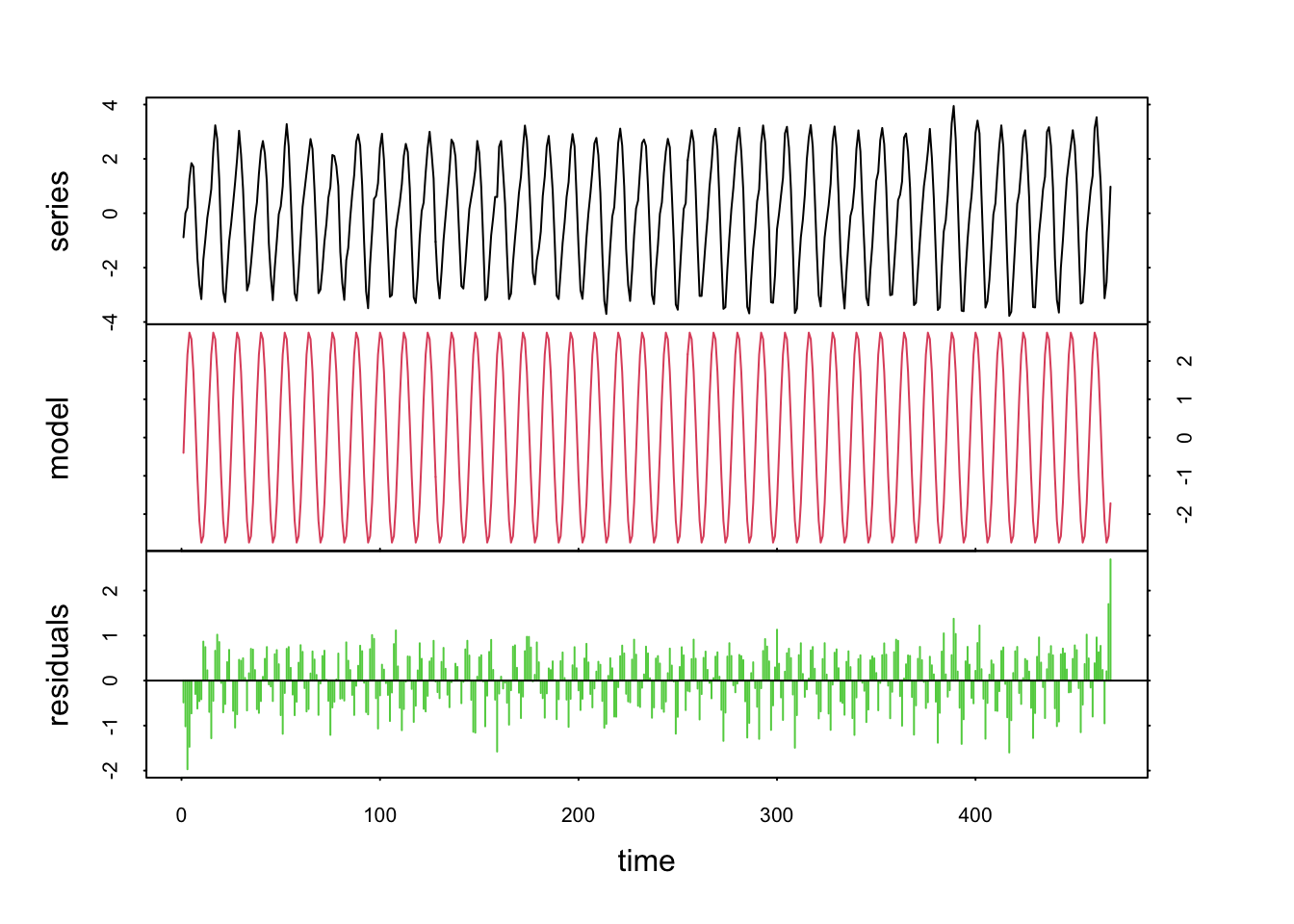
Ici, nos deux composantes se nomment model et residuals. Que donne l’analyse spectrale sur les résidus après avoir éliminé notre cycle saisonnier parfaitement sinusoïdal ?
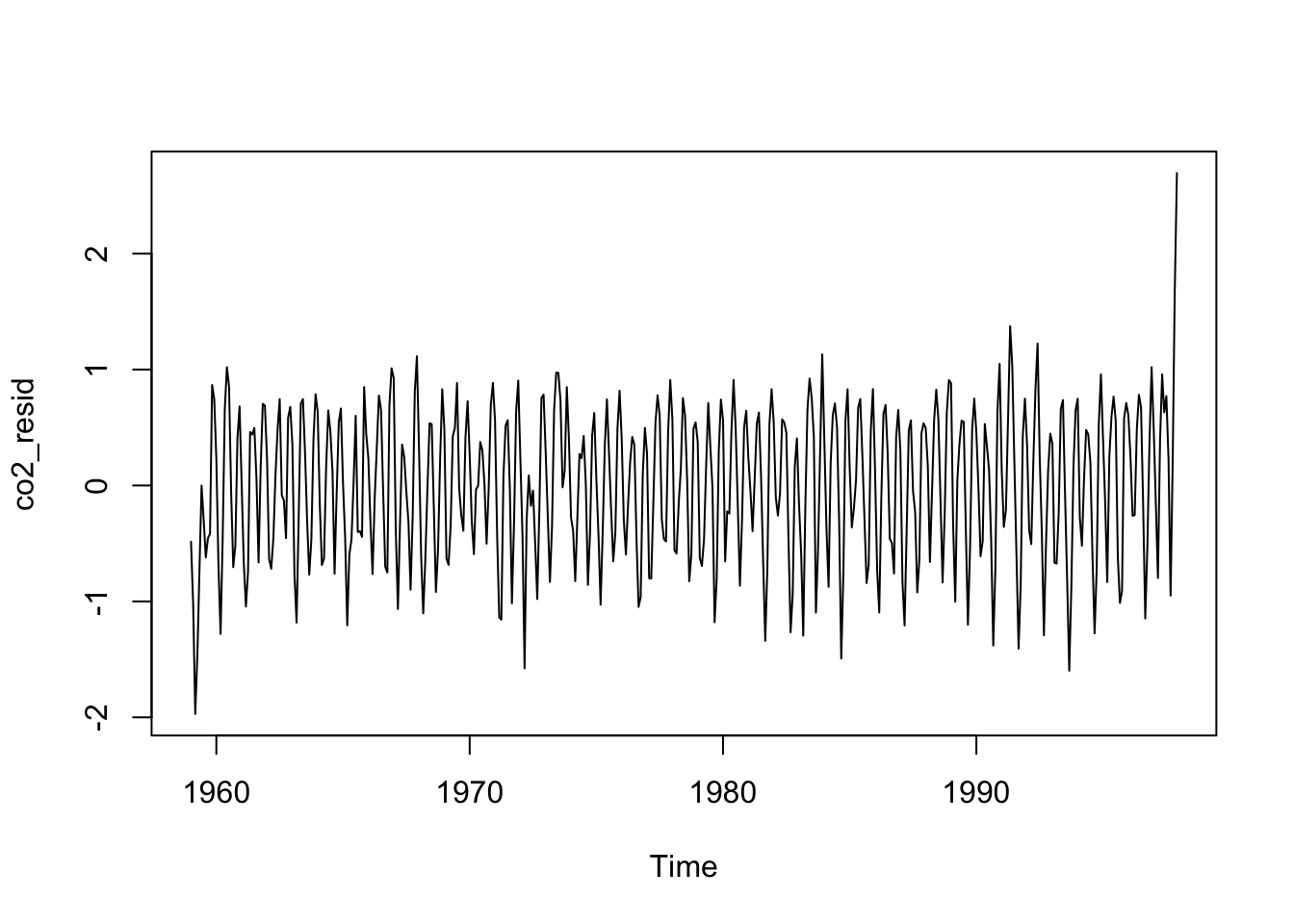
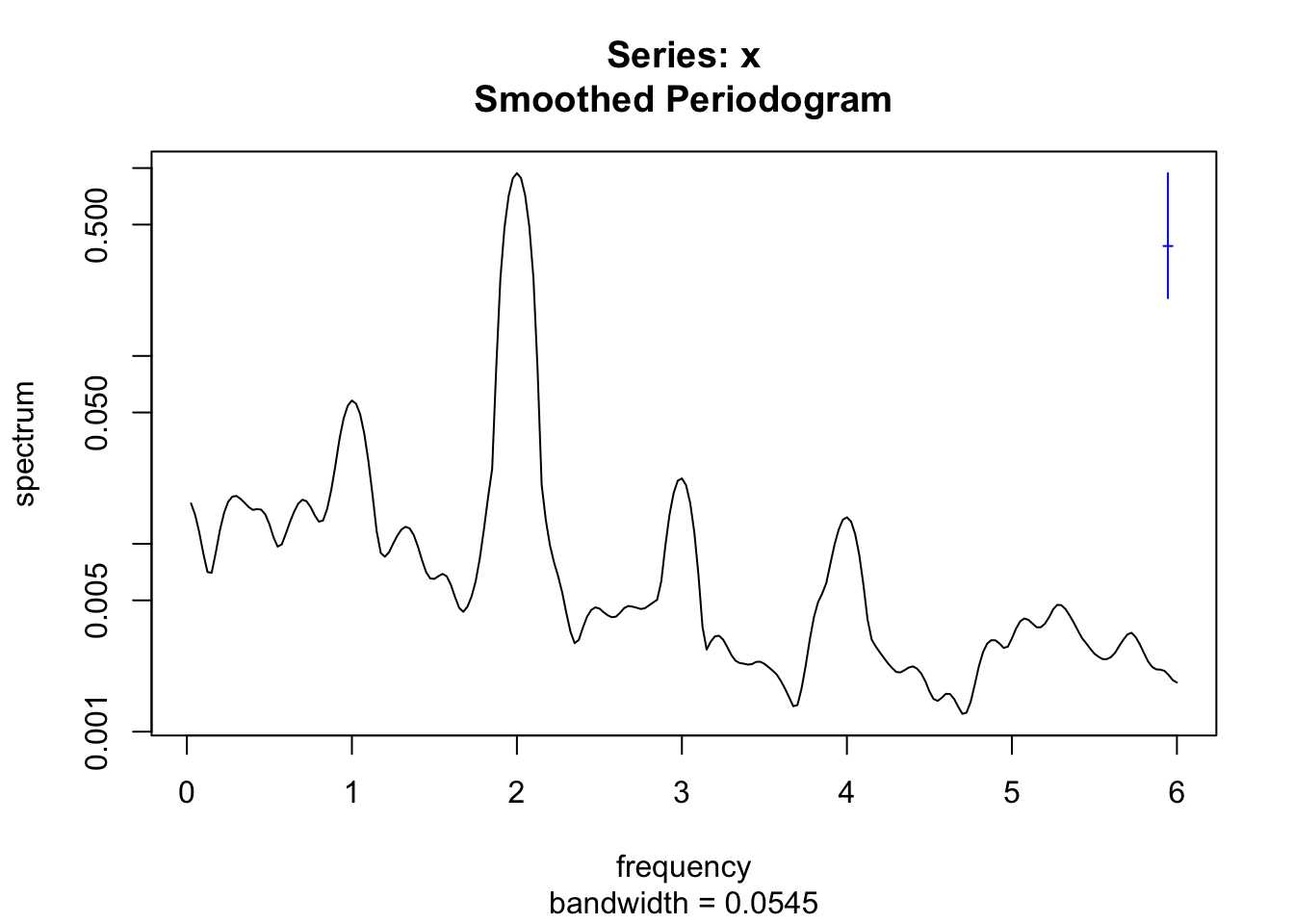
La composante saisonnière a bien été éliminée, mais une composante de période de 2 ans apparaît maintenant significative. Nous pouvons continuer la décomposition, mais à ce stade, il faut rester prudent, car les techniques de décomposition peuvent introduire des biais. Donc, nous devons nous demander si cette composante cyclique à deux ans est réelle ou s’il s’agit d’un artéfact des méthodes utilisées en amont. La réponse dépendra essentiellement des propriétés des techniques de décomposition… que nous allons étudier maintenant dans les sections suivantes de ce module.
Les plus pointilleux d’entre vous auront remarqué un comportement bizarre de nos résidus à la seconde étape de décomposition, au début et en fin de série avec des valeurs qui deviennent très extrêmes. Ceci est un effet de bord lié à la façon dont les moyennes mobiles opèrent en début et fin de série. Cela ne se voit pas trop dans les résidus de la première décomposition, mais un effet d’amplification du biais apparaît lors de la seconde décomposition. Vous devez toujours garder à l’esprit qu’aucune méthode de décomposition de série n’effectue un travail parfait. Des anomalies et des faux positifs (par exemple, des “cycles fantômes”) peuvent apparaître suite aux traitements réalisés antérieurement. Ici, nous pouvons utiliser la fonction window() et raccourcir la série aux deux bouts pour éliminer l’artéfact. Cela n’aura pas trop de conséquences néfastes. Mais restez toujours vigilant ! Pour cette raison, et parce que les séries combinant une tendance générale et un cycle saisonnier sont très fréquentes, les statisticiens ont mis au point des techniques qui permettent de séparer ces deux composantes des résidus sans artéfacts. L’une de ces techniques se nomme LOESS (prononcez “LO-ESSE”, pas “LEUS”). Voici ce que cela donne sur co2 (encore une fois, l’explication des arguments de la fonction sera réalisée plus loin).
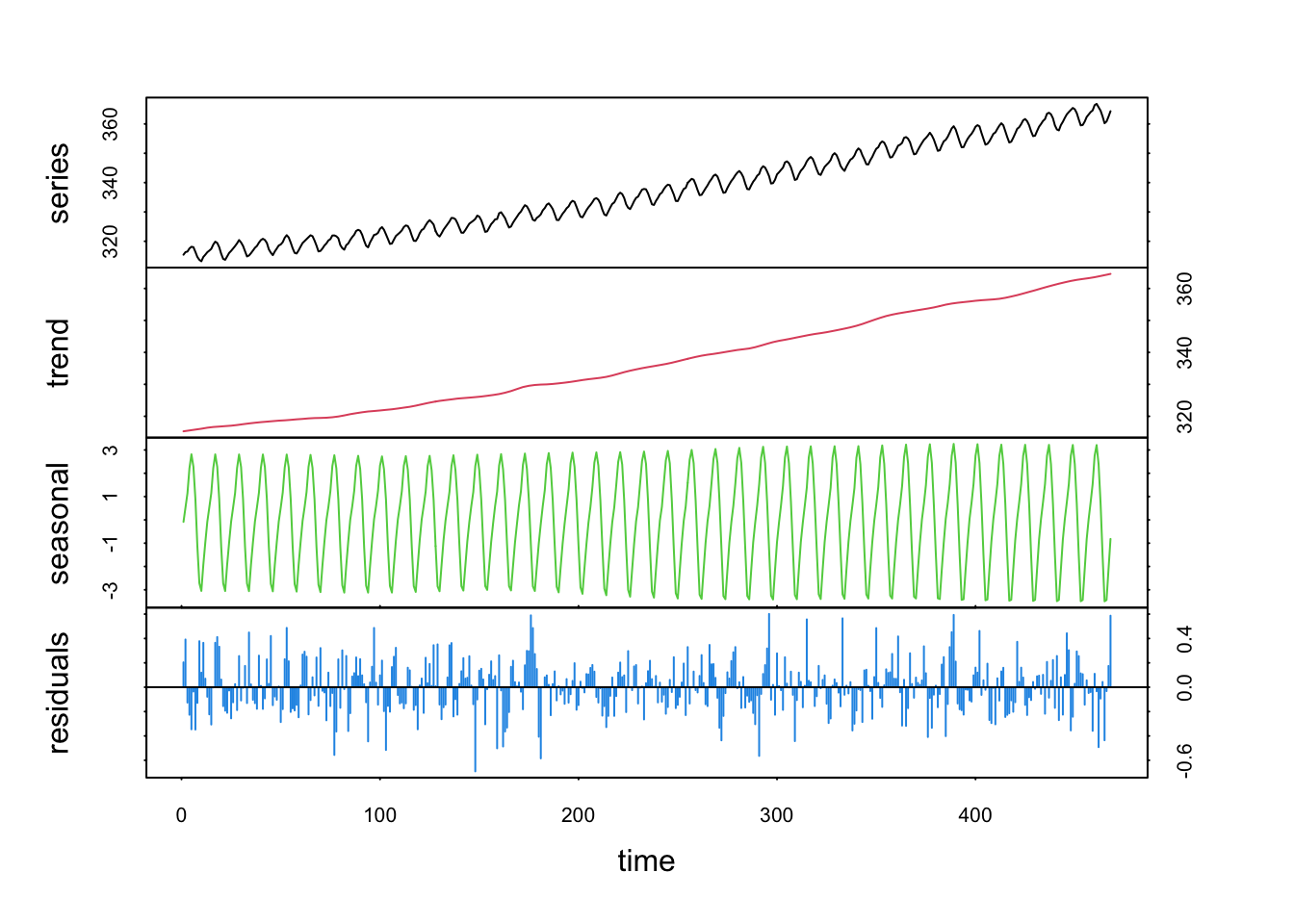
Contrairement à la décomposition précédente, notez que nous avons laissé plus de libertés au signal saisonnier en vert qui varie donc légèrement d’une année à l’autre. Nous aurions aussi pu imposer le même signal (mais pas nécessairement sinusoïdal) chaque année en indiquant s.window = "periodic". Naturellement ici, si les caractéristiques des composantes trend et seasonal sont assez évidentes, nous pourrions nous poser des questions concernant residuals. Comme cette série est stationnaire, nous pouvons directement en faire une analyse spectrale pour rechercher un ou plusieurs autres cycles de fréquence différente de un an.
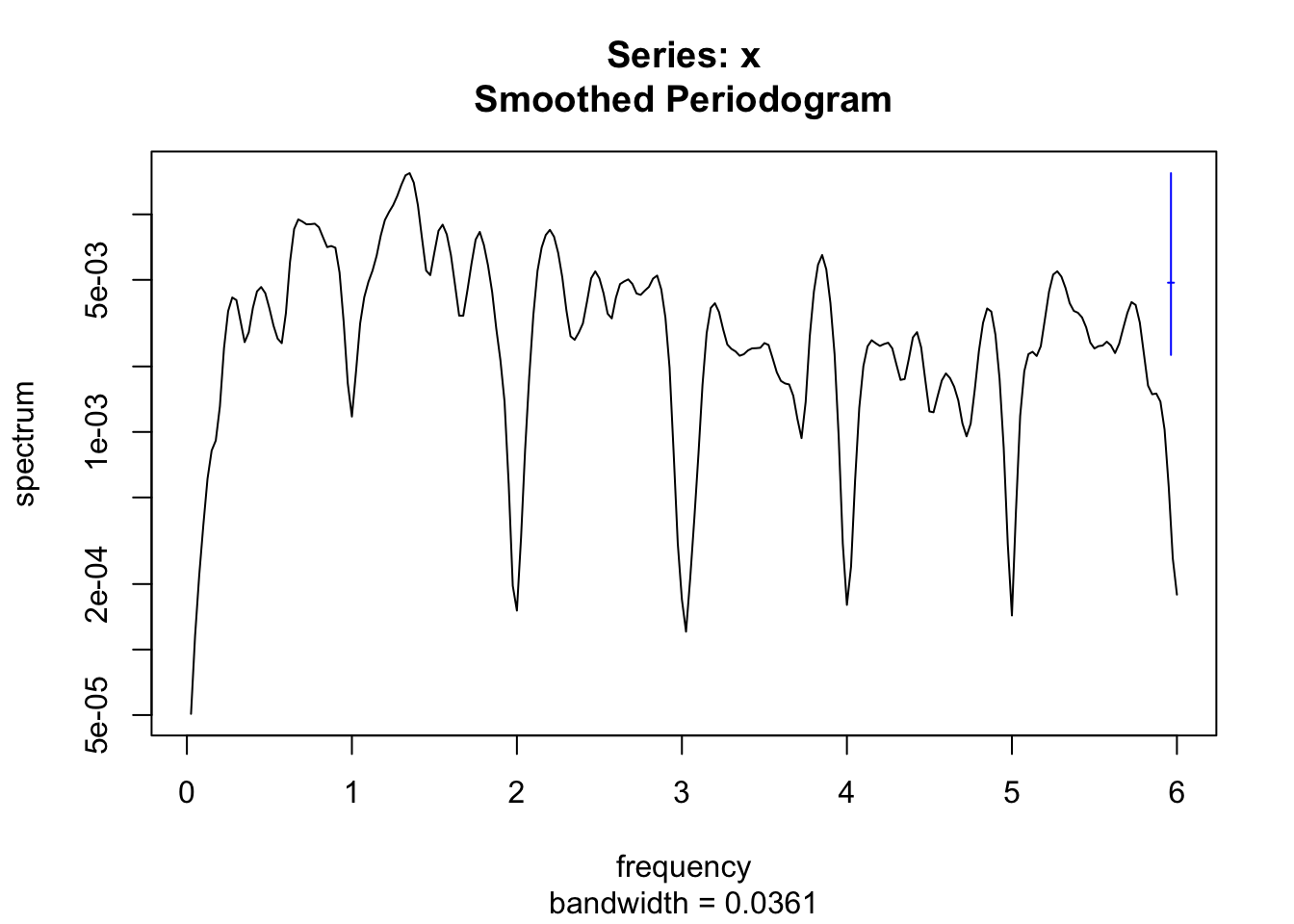
Ici, tout se passe comme si nous avions éliminé totalement tout signal de fréquence entière (1, 2, 3, …) et qu’ensuite d’autres signaux apparaissent. Ce sont probablement des cycles fantômes issus du traitement… tout comme le cycle à fréquence deux observé plus haut reste discutable. Gardez toujours votre esprit critique aiguisé en pareille situation ! Par exemple, quelle est l’étendue des signaux correspondants à nos trois composantes ? Pour la tendance, nous allons de 320 à 370 ppm, soit environ 50 ppm. Pour la composante saisonnière, l’amplitude du signal est de presque 3 ppm (le signal oscille entre 3 ppm et -3 ppm), soit une étendue de 6 ppm. Enfin, pour les résidus, l’échelle de l’axe s’étale de -0.6 à 0.4, soit 1 ppm, donc, une amplitude maximum de 0.5 ppm pour un éventuel cycle. Que peut-on encore extraire d’intéressant comme signal avec une si petite amplitude relative de presque un ordre de grandeur inférieur à l’amplitude du signal saisonnier qui, lui, est bien concret dans notre série ? Voilà le type de raisonnement logique que vous devez utiliser, au-delà de ce que les calculs vous montrent.
Avec tsd() vous avez plusieurs méthodes de décomposition disponibles, même si nous n’en avons abordé jusqu’ici que deux. Avec method= :
"average"pour les moyennes mobiles,"median"pour les médianes mobiles,"diff"pour la méthode des différence,"evf"pour le filtrage par les vecteurs propres de l’ACP,"reg"pour décomposer selon un modèle (droite ou courbe de régression),"loess"pour une décomposition plus complète en tendance générale, cycle saisonnier et résidus.
Toutefois, étant donné que les fonctions
decxxx()renvoient aussi des objets tsd, l’utilisateur avancé peut les préférer pour des questions de performance ou de simplicité dans ses propres scripts.↩︎