3.2 Courbes ROC
Avant d’aborder les courbes ROC, nous devons nous concentrer sur le seuil de détection (cutoff en anglais). Dans un classifieur à deux classes avec la forêt aléatoire, un vote à la majorité des arbres revient à dire que plus de la moitié des arbres a voté pour la classe retenue. Ceci correspond donc à un seuil de 50%. Mais qu’est-ce qui vous empêcherait d’utiliser un seuil différent ? Intuitivement, nous réalisons tout de suite que si nous durcissons le seuil pour la classe cible (par exemple, un individu ne sera déclaré de cette classe, appelée A, qu’à partir du moment où 70% ou plus des arbres ont voté en ce sens), nous aurons au final moins d’individus A dans notre prédiction. Cela aura probablement pour conséquence d’augmenter la précision (car plus de cas difficiles à discriminer auront été attribués à la classe B, or il est possible de montrer qu’une partie importante de l’erreur se situe justement dans ces cas moins nets). En revanche, cela diminue le rappel (car parmi ces cas difficile, il y a tout de même des A qui ne sont plus classés comme tels). Rappelez-vous toujours du fameux compromis rappel - précision. Choisir un seuil moins sensible, par exemple 30%, aura l’effet inverse d’augmenter les prédictions A, ainsi que le rappel, mais de diminuer précision et sensibilité. Sachant cela, nous pouvons nous demander s’il existe un seuil optimal. La courbe ROC permet de le déterminer.
La courbe ROC (pour “Receiver Operating Characteristic”) est une courbe qui représente le comportement de notre classifieur à deux classes pour tous les seuils de détection possibles. Si nous utilisons les probabilités d’appartenance à la classe cible renvoyées par notre classifieur au lieu des prédictions, nous pourrions choisir librement à partir de quelle probabilité nous considérons qu’un item est de cette classe. En prenant des seuils de 0 à 1 (ou 100%), nous balayons toutes les possibilités. À chaque seuil, nous pouvons calculer le taux de vrais positifs et le taux de faux positifs. La courbe ROC représente ces résultats avec le taux de faux positifs sur l’axe x et le taux de vrais positifs sur l’axe y. Pour illustrer cela, nous allons calculer la courbe ROC pour notre classifieur forêt aléatoire pima1_rf.
À vous de jouer !
Tout d’abord, il nous faut obtenir les “probabilités”. Selon les algorithmes ce sont réellement des probabilités, ou alors, des nombres entre 0 et 1 qui ont des propriétés similaires. Dans le cas de la forêt aléatoire, c’est la proportion des arbres qui ont voté pour la classe. On parlera alors plus justement d’un nombre qui quantifie l’appartenance à la classe (membership en anglais), plutôt que de probabilités. Voici comment nous pouvons obtenir ces appartenances :
# neg pos
# 1 0.990 0.010
# 2 0.292 0.708
# 3 0.942 0.058
# 4 0.238 0.762
# 5 0.304 0.696
# 6 0.398 0.602Nous utilisons le package {ROCR} (déjà chargé via SciViews::R("ml")) qui demande uniquement les appartenances à la classe cible (ici pos, donc la seconde colonne), ainsi qu’un vecteur indiquant par 0 ou 1 si l’individu appartient effectivement ou non à cette classe cible. C’est l’objet prediction. À partir de là, nous calculons un objet performance en indiquant les deux métriques que nous voulons utiliser (“true positive rate” tpr et “false positive rate” fpr pour la courbe ROC), et nous réalisons ensuite le graphique.
# 1) Formater les prédictions pour ROCR
pima1_rf_predobj <- prediction(pima1_rf_mem[, 2], pima1$diabetes == "pos")
# 2) Calculer les performances avec les deux métriques tpr et fpr
pima1_rf_perf <- performance(pima1_rf_predobj, "tpr", "fpr")
# 3) Tracer notre graphique ROC
plot(pima1_rf_perf)
abline(a = 0, b = 1, lty = 2)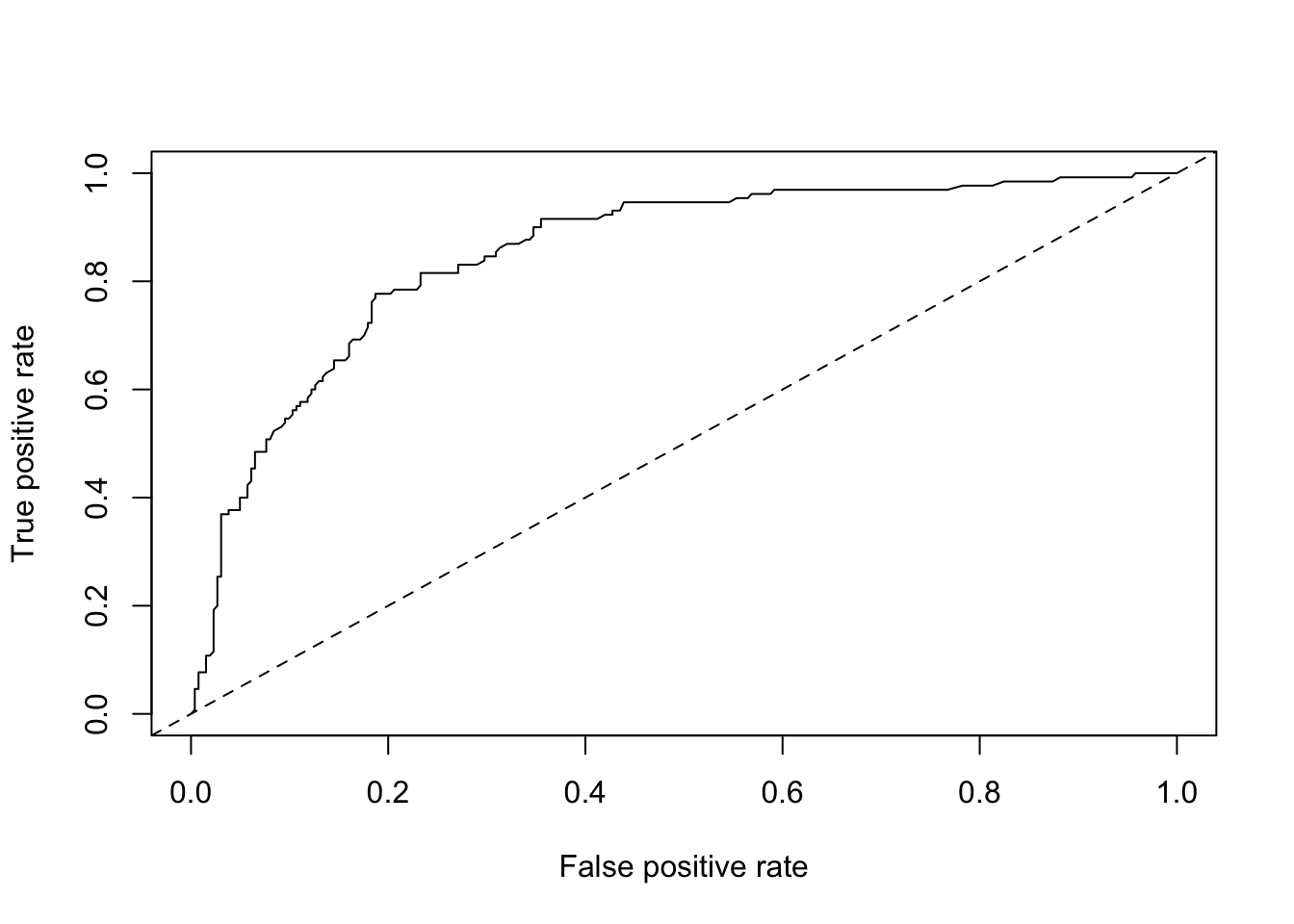
Le trait pointillé représente ce que donnerait un classifieur de référence qui classe en pos ou neg au hasard, et donc, il obtient autant de faux positifs que de vrais positifs quel que soit le seuil choisi. En dessous, nous ferions moins bien que le hasard. Au-dessus, notre classifieur est meilleur. Et plus nous nous rapprochons du coin supérieur gauche du graphique avec notre courbe, meilleur sera notre classifieur (plus haut taux de vrais positifs pour plus bas taux de faux positifs). Ainsi le choix du seuil peut se faire pour un point de la courbe qui s’approche le plus du coin supérieur gauche.
Une façon de quantifier globalement les performances de notre classifieur quel que soit le seuil est de calculer l’aire sous cette courbe. Pour un classifieur au hasard de référence, elle sera de 0.5 puisque le triangle inférieur délimité par le trait pointillé représente la moitié de l’aire totale du graphique. Plus l’aire sous la courbe (AUC ou Area Under the Curve en anglais) se rapprochera de un, meilleur sera notre classifieur. Voici une des façons de calculer l’AUC dans R :
# Setting levels: control = neg, case = pos# Setting direction: controls < cases# Area under the curve: 0.852Si vous voulez, l’AUC est un peu comme le R2 de la régression linéaire : pour un même jeu de données, nous pouvons superposer les courbes de deux ou plusieurs classifieurs sur le graphique, et calculer leurs AUCs respectifs pour nous aider à choisir le meilleur. Par contre, avec deux jeux de données différents (proportions par classes différentes), les valeurs ne sont plus comparables. Ainsi, si nous voulons comparer notre classifieur issu de pima1b avec celui de pima1, nous devons d’abord réajuster les proportions pour que les deux soient comparables, voir ici.
pima1b_rf_mem <- cvpredict(pima1b_rf, cv.k = 10, type = "membership")
# Tableau membership + vraies valeurs
pima1b_rf_mem <- dtx(membership = pima1b_rf_mem[, 2], diabetes = pima1b$diabetes)
# Rééchantillonnage pour rétablir les bonnes proportions
# (calcul un peu compliqué, mais pas besoin de comprendre les détails ici
# pour comprendre la logique générale du calcul effectué)
set.seed(36433)
pima1b_rf_mem %>.%
as_dtf(.) %>.% # Il faut un data.frame ici car unnest() ne fonctionne pas sur un data.table
group_by(., diabetes) |> nest() |> ungroup() %>.%
mutate(., n = pima_prior * nrow(pima1)) %>.%
mutate(., samp = purrr::map2(data, n, sample_n, replace = TRUE)) %>.%
select(., -data) %>.%
unnest(., samp) ->
pima1b_resampled
table(pima1b_resampled$diabetes)#
# neg pos
# 255 136Une fois le réajustement des proportions réalisé dans pima1b_resampled, nous pouvons superposer les deux courbes ROC pour nos classifieurs pima1_rf et pima1b_rf. Pour superposer un graphique sur l’autre, utiliser l’argument add = TRUE pour le second avec les fonctions graphiques de R de base utilisées ici.
pima1b_rf_predobj <- prediction(pima1b_resampled$membership,
pima1b_resampled$diabetes == "pos")
pima1b_rf_perf <- performance(pima1b_rf_predobj, "tpr", "fpr")
# Graphique relatif à pima1
plot(pima1_rf_perf, col = "darkgreen")
# Ajout de celui relatif à pima1b sur le même graphique
plot(pima1b_rf_perf, col = "darkred", add = TRUE)
abline(a = 0, b = 1, lty = 2)
legend("bottomright", inset = 0.1, legend = c("pima1", "pima1b"), lty = 1,
col = c("darkgreen", "darkred"))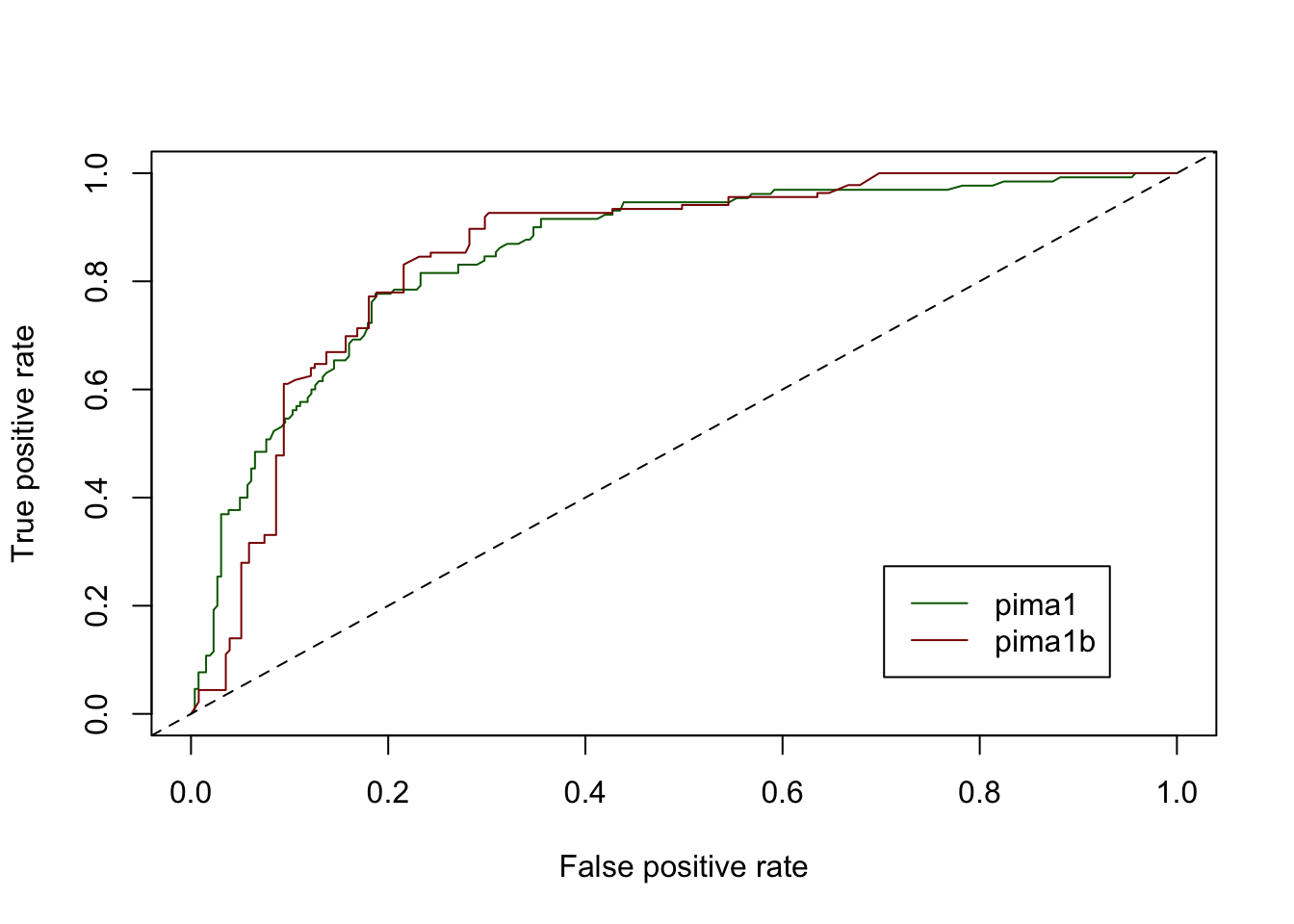
# Setting levels: control = neg, case = pos# Setting direction: controls < cases# Area under the curve: 0.8526Nous pouvons observer que notre second classifieur pima1b_rf est effectivement globalement légèrement plus performant que pima1_rf, avec toutefois des précautions d’usage puisque les données utilisées ne sont pas strictement identiques. Seulement les proportions relatives dans les deux classes ont été alignées entre les deux courbes. Par contre, selon le seuil de détection choisi, le classifieur pima1_rf peut localement égaler, ou même dépasser légèrement les performances de pima1b_rf. De manière générale, les courbes ROC seront parfaitement utilisables sans ajustement nécessaire par contre, pour comparer deux modèles différents obtenus à partir d’exactement les mêmes données.