2.2 Différents algorithmes

Les algorithmes de classification supervisée se subdivisent en trois grandes classes :

ceux qui utilisent un modèle (linéaire ou non linéaire) sous-jacent pour mettre en relation les attributs et les classes. Par exemple, l’analyse discriminante linéaire que nous connaissons déjà appartient à cette catégorie. Nous verrons également les machines à vecteurs supports et les réseaux de neurones dans cette catégorie.
ceux qui font appel à un indice de similarité calculé entre les individus (attribution de la classe correspondant aux individus les plus ressemblants à celui qu’on teste). Ce sont les techniques dites du plus proche voisin et de la quantification vectorielle (voir ci-après dans ce module).
enfin, les techniques qui définissent une suite de règle de division dichotomique du jeu de données (qui se matérialisent par un ou plusieurs arbres de décision). Il s’agit du partitionnement récursif et de la forêt aléatoire, par exemple. Nous aborderons ces méthodes à la fin du module.

Nous avons déjà étudié l’analyse discriminante linéaire dans le précédent module et nous allons découvrir ici quelques autres algorithmes de chaque catégorie, ainsi que dans le module suivant. Enfin, nous mettrons tout cela en musique pour étudier différents algorithmes de classification en pratique, en vue de choisir celui qui nous semble le plus adéquat pour le cas étudié.

2.2.1 Indiens diabétiques

Afin d’explorer et comparer l’utilisation de différents algorithmes de classification supervisée, nous reprendrons notre jeu de données pima concernant une population d’Amérindiens qui sont connus pour compter un haut taux d’obèses et de diabétiques. Nous avions déjà utilisé ces données pour illustrer l’ACP dans le cours de Science des Données biologiques II. Pour rappel, le jeu de données se présente comme suit :

SciViews::R("ml")
pima <- read("PimaIndiansDiabetes2", package = "mlbench")
tabularise$headtail(pima)

pregnant	glucose	pressure	triceps	insulin	mass	pedigree	age	diabetes
6	148	72	35		33.6	0.627	50	pos
1	85	66	29		26.6	0.351	31	neg
8	183	64			23.3	0.672	32	pos
1	89	66	23	94	28.1	0.167	21	neg
0	137	40	35	168	43.1	2.288	33	pos
...	...	...	...	...	...	...	...	...
10	101	76	48	180	32.9	0.171	63	neg
2	122	70	27		36.8	0.340	27	neg
5	121	72	23	112	26.2	0.245	30	neg
1	126	60			30.1	0.349	47	pos
1	93	70	31		30.4	0.315	23	neg
Premières et dernières 5 lignes d'un total de 768

Nous avons huit variables quantitatives (discrète comme pregnant, ou continues pour les autres) et une variable qualitative diabetes. Voici quelques informations sur ces différentes variables :

diabetes, variable qualitative à deux niveaux indique si l’individu est diabétique (pos) ou non (neg). C’est naturellement la variable réponse que l’on cherchera à prédire ici,
pregnant est le nombre de grossesses que cette femme a eues (il s’agit uniquement d’un échantillon de femmes de 21 ans ou plus),
glucose est le taux de glucose dans le plasma sanguin (test standardisé renvoyant une valeur sans unités),
pressure est la pression sanguine diastolique, en mm de mercure,
triceps est l’épaisseur mesurée d’un pli de peau au niveau du triceps en mm. Il s’agit d’une mesure permettant d’estimer l’obésité, ou en tous cas, la couche de graisse sous-cutanée à ce niveau,
insulin est la détermination de la quantité d’insuline deux heures après prise orale de sucre dans un test standardisé, en µU/mL,
mass est en réalité l’IMC, indice de masse corporelle que vous connaissez bien (masse/ taille²), en kg/m², un autre indice d’obésité couramment employé,
pedigree est un indice de prédisposition au diabète établi en fonction des informations sur la famille (sans unités),
age est l’âge de l’Amérindienne exprimé en années.

Du point de vue du balancement des observations, nous avons ceci :

table(pima$diabetes)

# 
# neg pos 
# 500 268

Nous avons plus de cas négatifs que de positifs et pourrions souhaiter balancer les deux classes. La différence n’est cependant pas à ce point dramatique et nous continuerons dans cet exemple avec les données telles quelles.

Ce jeu de données contient 768 cas, mais deux variables (triceps et insulin) ont un très grand nombre de valeurs manquantes comme nous le voyons ci-dessous.

naniar::vis_miss(pima)

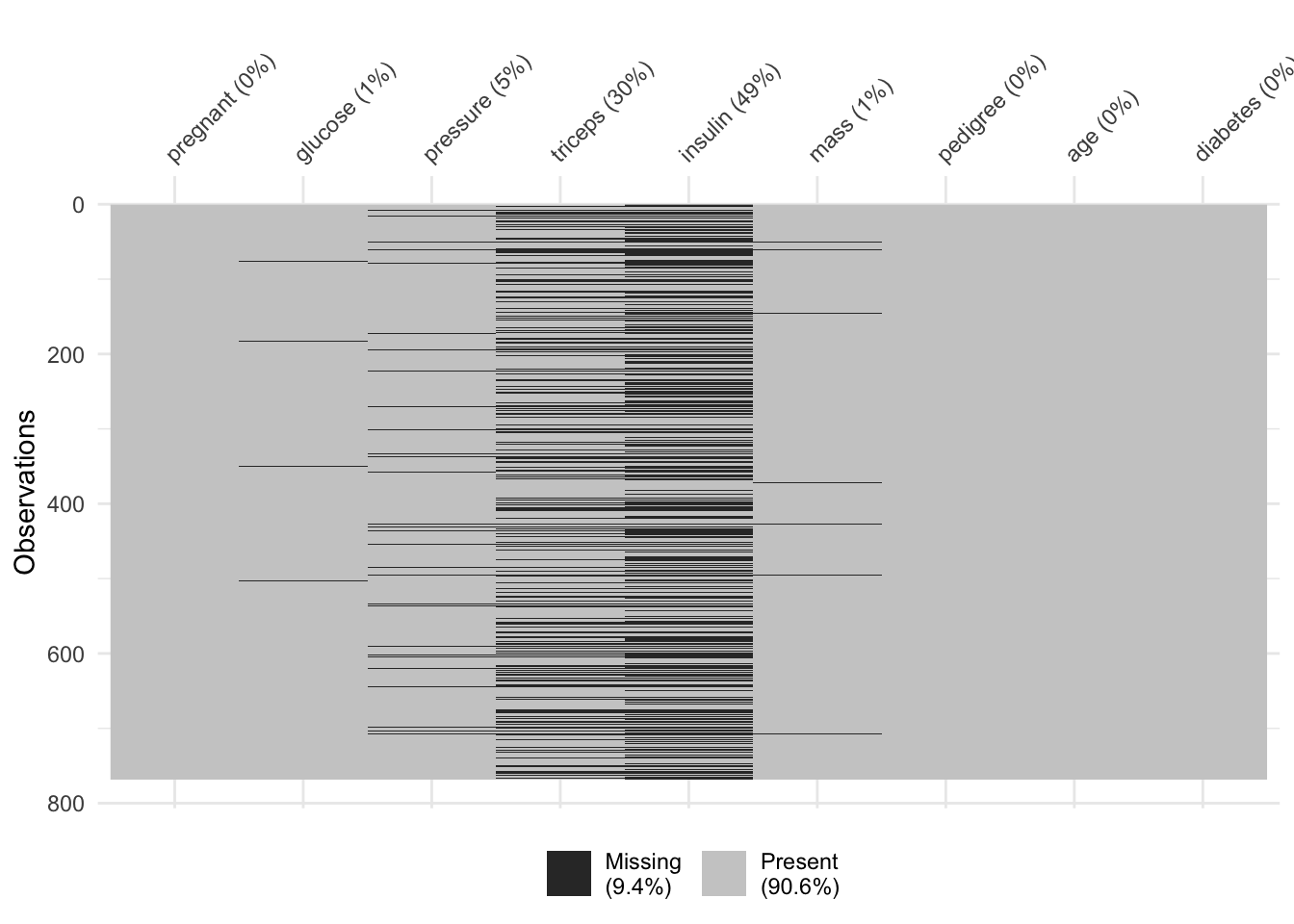
Comme pour l’ACP, nos sets d’apprentissage et de test ne peuvent pas contenir de valeurs manquantes. Si nous utilisons drop_na() sur tout le tableau, toute ligne contenant au moins une valeur manquante sera éliminée. Cela donne ceci :

pima1 <- sdrop_na(pima)
nrow(pima1)

# [1] 392

Nous avons certes un tableau propre, mais nous avons perdu près de la moitié des données ! Or nous n’avons jamais assez de données en classification supervisée. Nous pourrions aussi considérer la possibilité de laisser tomber les colonnes qui contiennent trop de valeurs manquantes. En première approche, afin de déterminer si la perte de ces variables pourrait être préjudiciable à notre analyse, nous pourrions inspecter la matrice de corrélation.

pima1 %>.%
  sselect(., -diabetes) %>.%
  correlation(.) %>.%
  plot(.)

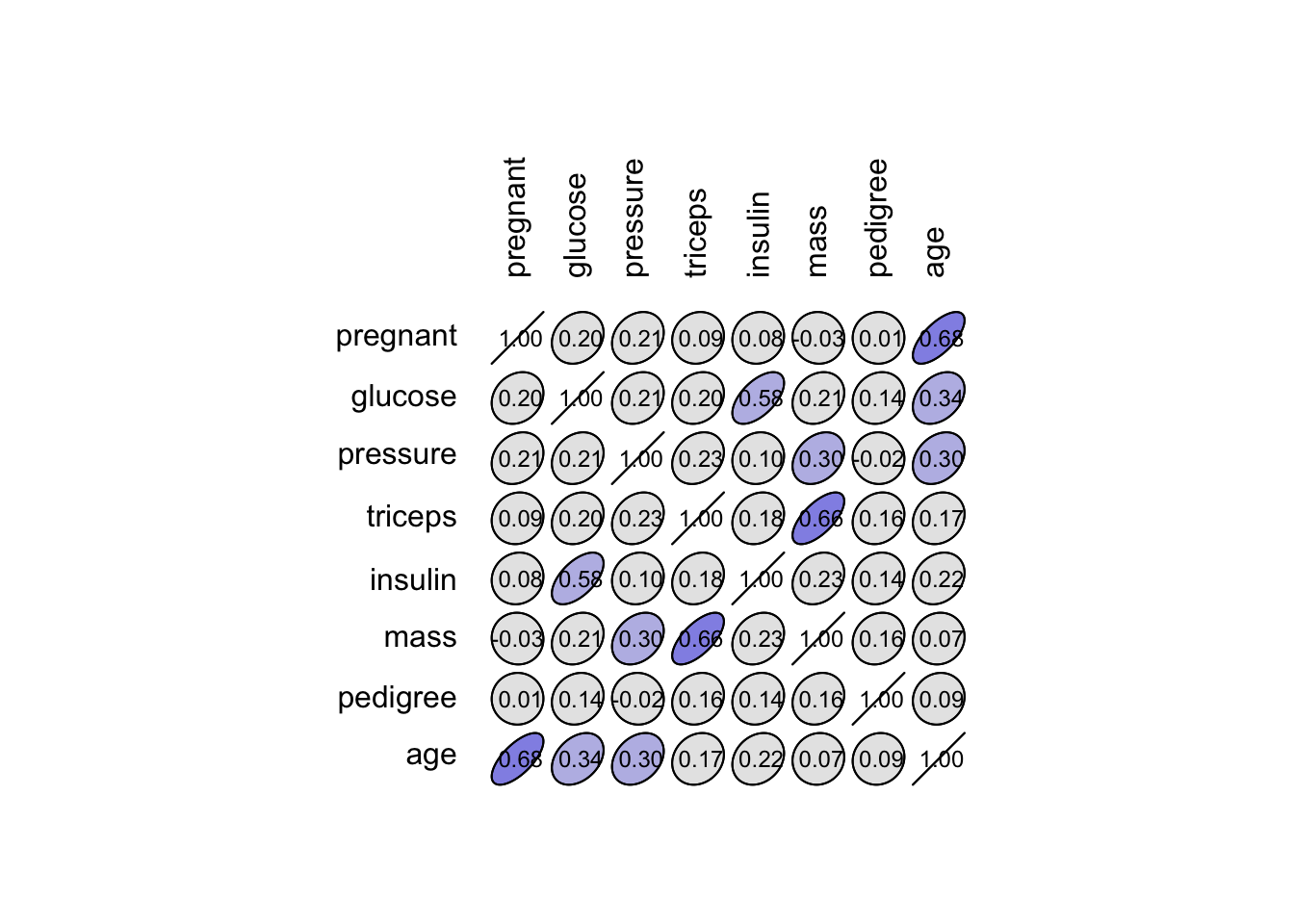
Nous observons que triceps est le plus fortement corrélé à mass, ce qui est logique puisqu’il s’agit de deux mesures différentes de l’obésité.

chart(data = pima1, triceps ~ mass %color=% diabetes) +
  geom_point() +
  stat_smooth(method = "lm", formula = y ~ x)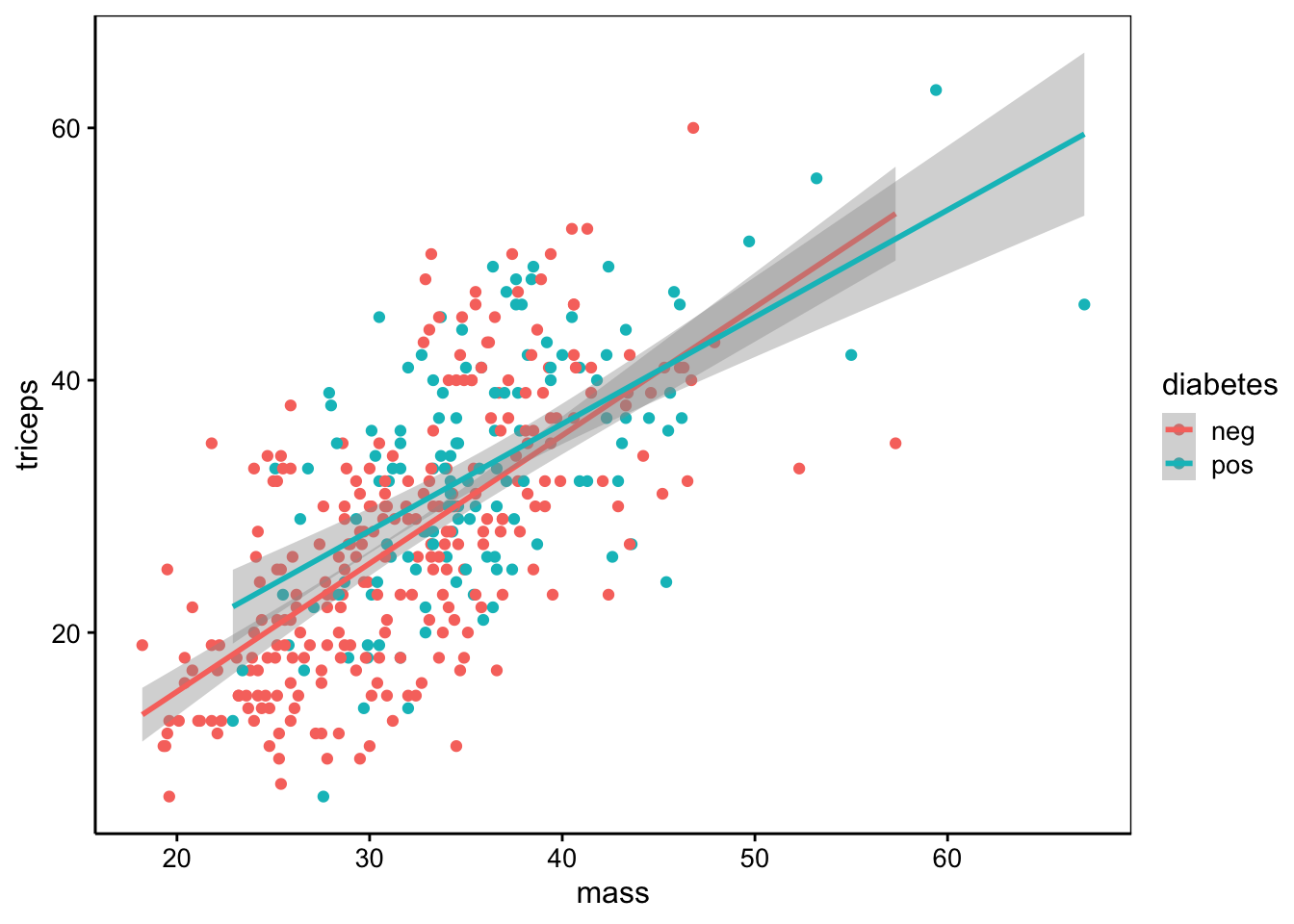

De même, insulin est corrélée à glucose, également deux tests qui étudient le profil de variation du sucre dans le sang et d’une hormone associée.

chart(data = pima1, insulin ~ glucose %color=% diabetes) +
  geom_point() +
  stat_smooth(method = "lm", formula = y ~ x)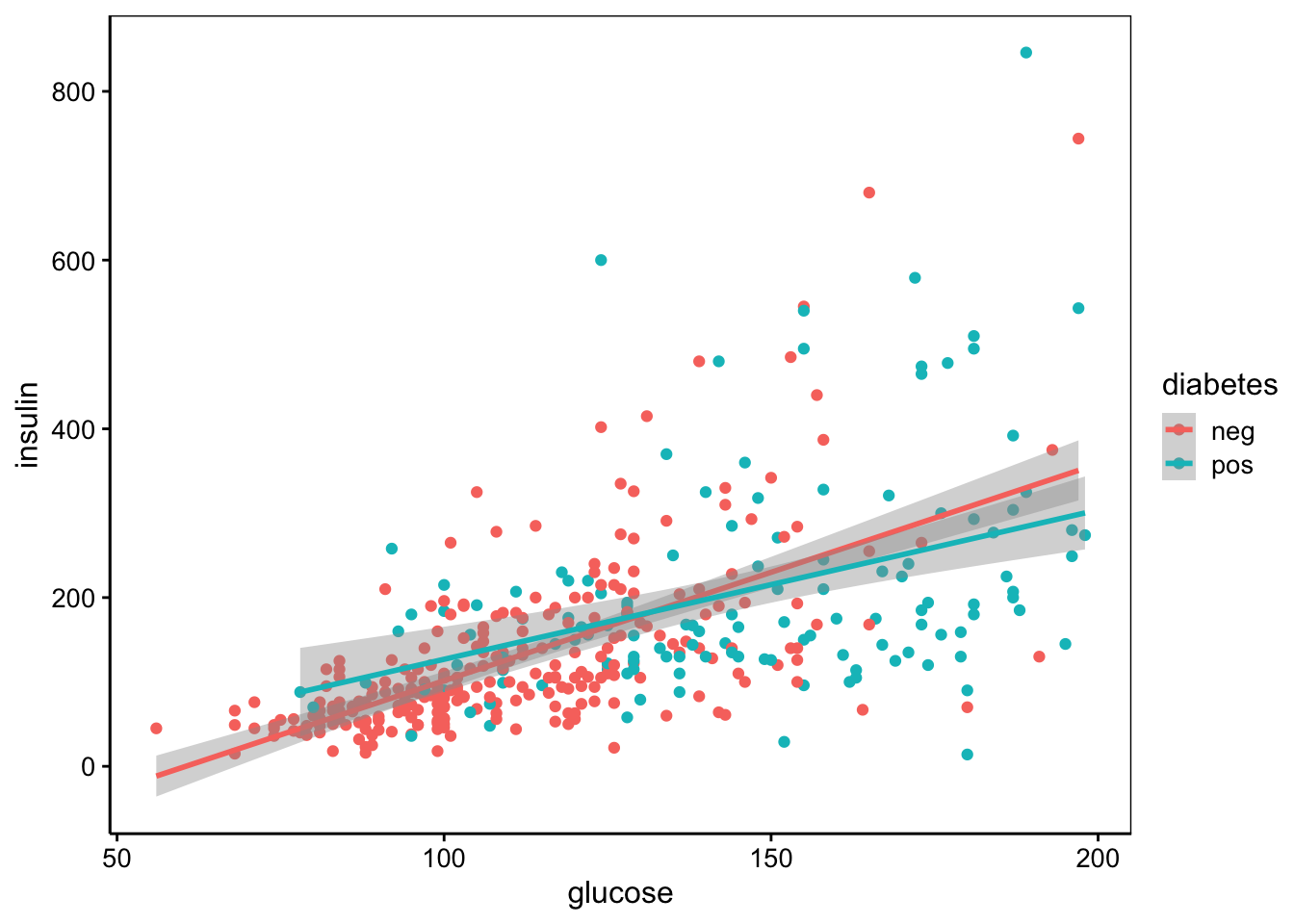

Enfin, et pour être complet, notons aussi que les variables pregnant et age sont également corrélées (0,68). C’est assez logique que les filles moins âgées aient eu moins de grossesses que les autres.

Cependant, les corrélations de Pearson sont moyennes (0,66, 0,58, et 0,68 respectivement) et les nuages de points assez dispersés. Nous pourrions donc nous demander s’il vaut mieux garder plus de données avec moins de variables pour notre apprentissage et test… nous allons créer pima2 sans insulin et triceps et nous comparerons l’analyse faite avec pima1 (plus de variables, moins de cas) et pima2 (moins de variables, plus de cas).

pima %>.%
  sselect(., -insulin, -triceps) %>.%
  sdrop_na(.) %->%
  pima2
nrow(pima2)

# [1] 724

Dans ce second jeu de données, nous avons pu tout de même conserver 724 cas. L’ACP que nous avions réalisée sur ces données nous montrait que la variance se répartir à 53% sur deux axes, mais qu’il faut considérer cinq axes pour capturer 90% de cette variance. Ceci suggère, comme la matrice de corrélation, que les différentes variables apportent chacune une information complémentaire. Au final, nous n’observions pas de séparation nette sur le graphique des individus de l’ACP entre la sous-population diabétique et celle qui ne l’est pas. Nous allons reconsidérer la question ici à l’aide de techniques plus spécifiques visant à prédire qui est diabétique ou non en fonction des huit (pima1) ou six (pima2) attributs à disposition, et ce, à l’aide de différents algorithmes de classification supervisée. Commençons par voir ce que cela donne avec l’ADL que nous connaissons maintenant bien, en utilisation, une validation croisée dix fois.

set.seed(364)
pima1_lda <- mlLda(data = pima1, diabetes ~ .)
pima1_lda_conf <- confusion(cvpredict(pima1_lda, cv.k = 10), pima1$diabetes)
plot(pima1_lda_conf)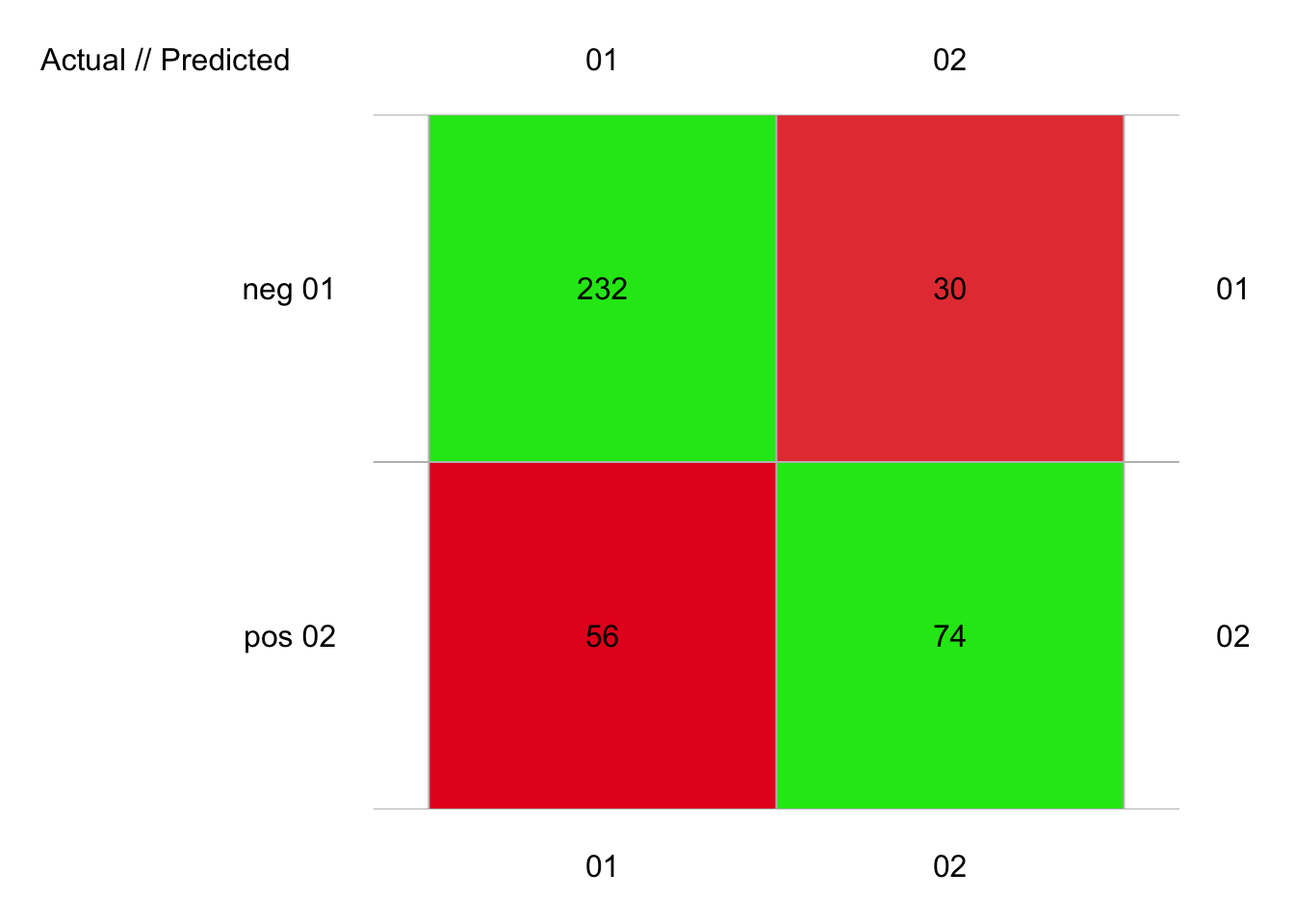

summary(pima1_lda_conf, type = c("Fscore", "Recall", "Precision"))

# 392 items classified with 306 true positives (error = 21.9%)
# 
# Global statistics on reweighted data:
# Error rate: 21.9%, F(micro-average): 0.743, F(macro-average): 0.738
# 
#        Fscore    Recall Precision
# neg 0.8436364 0.8854962 0.8055556
# pos 0.6324786 0.5692308 0.7115385

Et avec pima2, cela donne :

set.seed(2673)
pima2_lda <- mlLda(data = pima2, diabetes ~ .)
pima2_lda_conf <- confusion(cvpredict(pima2_lda, cv.k = 10), pima2$diabetes)
plot(pima2_lda_conf)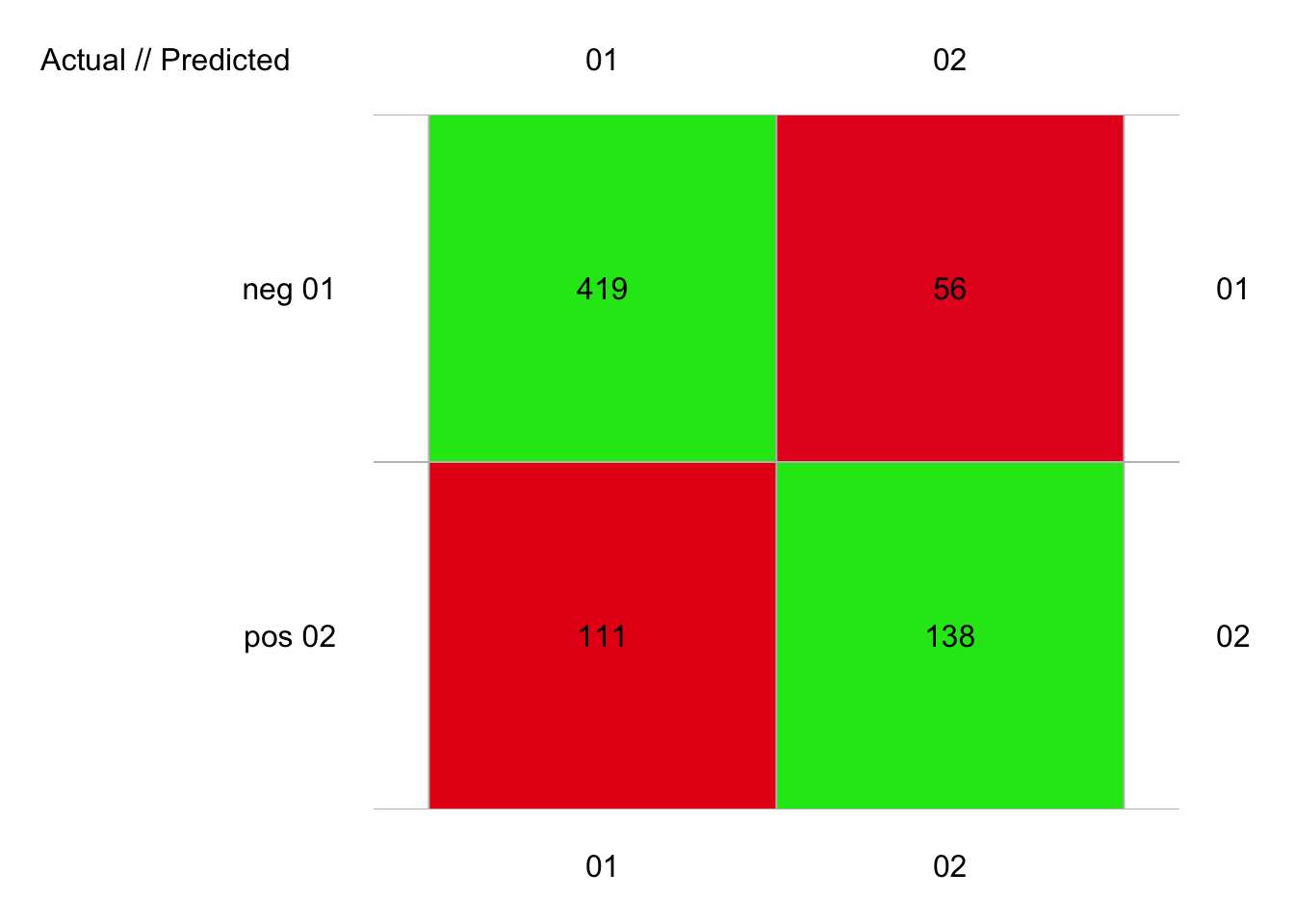

summary(pima2_lda_conf, type = c("Fscore", "Recall", "Precision"))

# 724 items classified with 557 true positives (error = 23.1%)
# 
# Global statistics on reweighted data:
# Error rate: 23.1%, F(micro-average): 0.734, F(macro-average): 0.728
# 
#        Fscore    Recall Precision
# neg 0.8338308 0.8821053 0.7905660
# pos 0.6230248 0.5542169 0.7113402

Nous avons 22% d’erreur avec pima1 et 23% d’erreur avec pima2. Ces résultats se tiennent dans le cas présent. Ce n’est évidemment pas toujours le même résultat. Nous allons voir ce que cela donne avec d’autres algorithmes de classification dans la suite.