6.5 Interpolation spatiale
Parmi les nombreuses techniques statistiques appliquées aux données géoréférencées (autocorrélation spatiale, analyse de motifs de points, modélisation spatiale et spatio-temporelle, classification et segmentation de zones géographiques …) nous nous attarderons sur l’une des plus utiles : l’interpolation spatiale. Son principe consiste à interpoler la variation d’une mesure quantitative dans une zone géographique donnée à partir de mesures éparses. Cette interpolation spatiale permet de construire ensuite des cartes bien plus percutantes.
Il est en effet plutôt rare d’avoir une couverture dense de mesures sur une grande étendue géographique. Si nous prenons l’exemple de données météorologiques, mis à part l’utilisation d’images satellites, les données sont la plupart du temps obtenues à partir d’un réseau de stations plus ou moins dense. Dans notre exemple, nous nous intéresserons à la pluviométrie exprimée en mm d’eau par an. Un pluviomètre est un appareil simple qui recueille l’eau tombée du ciel sur une surface donnée et qui contient un tube gradué en mm. Il suffit alors de lire la valeur après un laps de temps donné pour connaître la quantité cumulée d’eau qui est tombée du ciel.

6.5.1 Où pleut-il au Maroc ?
Les données que nous allons traiter comme exemple ne sont pas dénuées d’intérêt pour le botaniste, le zoologiste, ou encore, l’écoconseiller, qui ont tous besoin de données environnementales pour comprendre la distribution des plantes et des animaux. Bien sûr, la technique est également utilisable dans bien d’autres contextes : distribution des espèces et biodiversité, gradients de pollution, progression d’une épidémie, etc.
Sur base de nos données relatives au Maroc que nous avons utilisées comme exemple jusqu’ici, nous avons également mrain qui propose des mesures de pluviométrie en mm/an enregistrées en une quarantaine de stations météorologiques réparties sur tout le territoire, mais de manière inégale. Cet objet geopoints doit être converti en sf comme à notre habitude.
# Simple feature collection with 43 features and 1 field
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -17.03 ymin: 20.52 xmax: -1.93 ymax: 35.78
# Geodetic CRS: +proj=longlat +datum=WGS84
# First 10 features:
# rain geometry
# 1 57.3 POINT (-13.22 27.17)
# 2 138.5 POINT (-10.12 29.37)
# 3 29.4 POINT (-15.93 23.72)
# 4 818.7 POINT (-5.8 35.78)
# 5 682.4 POINT (-5.9 35.72)
# 6 653.2 POINT (-6.13 35.18)
# 7 961.4 POINT (-5.3 35.08)
# 8 299.3 POINT (-3.85 35.18)
# 9 261.8 POINT (-1.93 34.78)
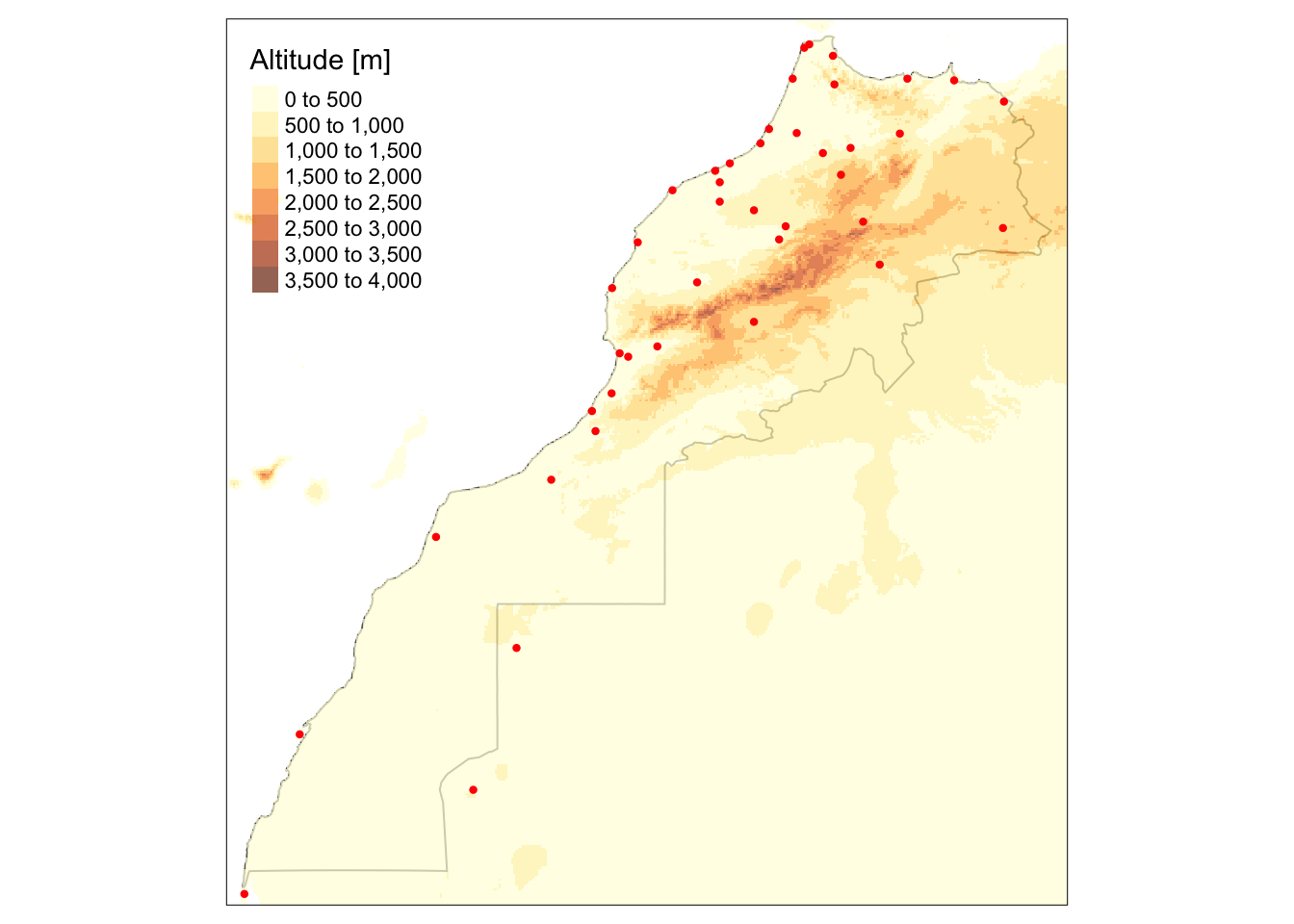
# 10 541.1 POINT (-6.6 34.3)Nous pouvons rajouter ces données de pluviométrie sur notre carte du Maroc avec {tmap}. Si nous utilisons tm_dots(), nous localisons simplement les stations météorologiques pour lesquelles nous avons des données de pluviométrie annuelle :
Plus intéressants, avec tm_bubbles() nous visualisons également l’intensité des pluies à l’aide du diamètre des cercles :
m_map3 <- m_map2 +
tm_shape(m_rain) +
tm_bubbles(col = "darkblue", size = "rain",
legend.size.is.portrait = TRUE, title.size = "Pluie [mm/an]")
m_map3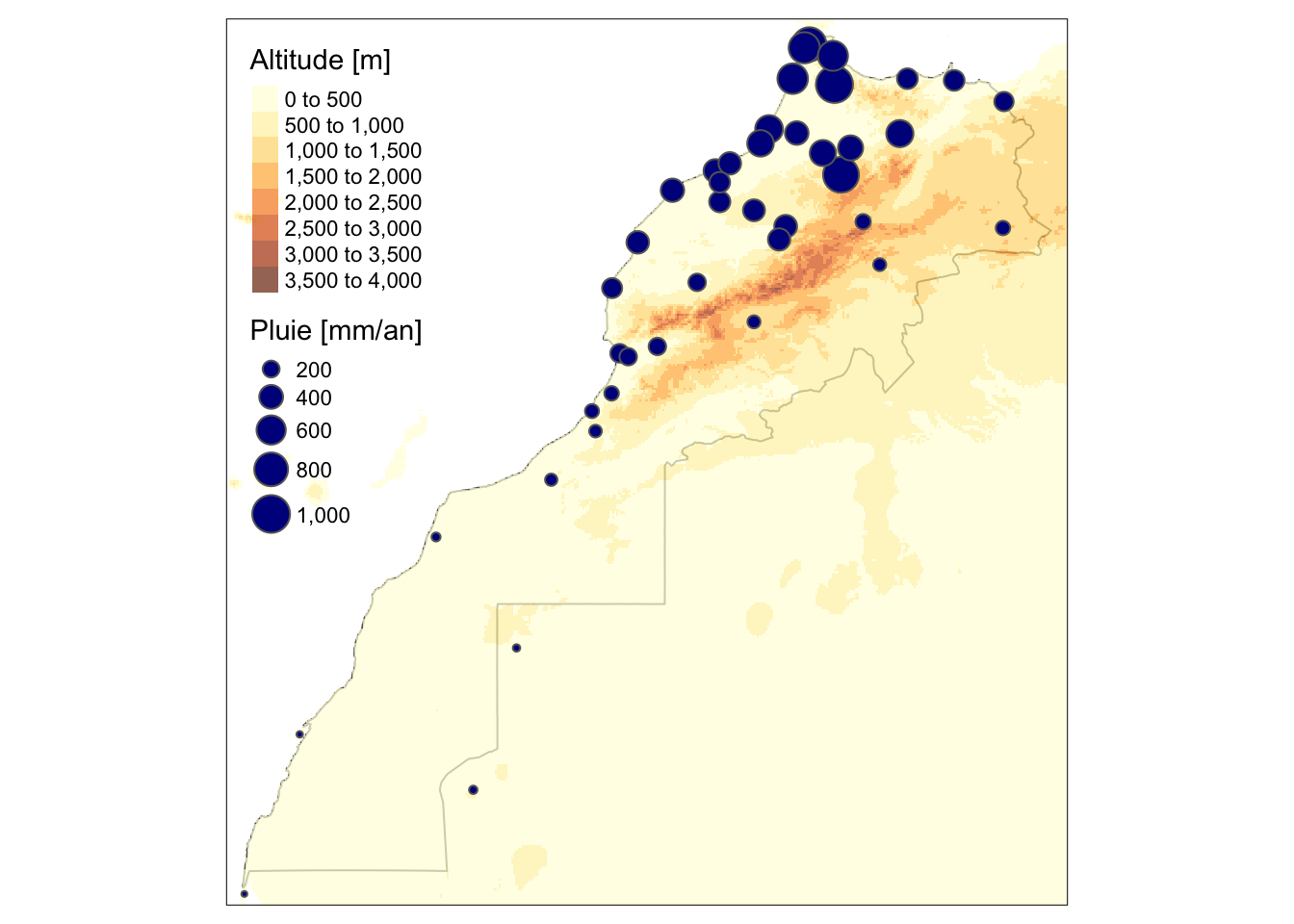
Comme nous pouvons le voir, les données sont très éparses. Ce serait pourtant utile d’avoir une couverture de l’estimation de la pluviométrie sur tout le territoire marocain. Pour cela, nous devons utiliser l’interpolation spatiale pour créer un raster sur base de ces données.
L’interpolation spatiale est possible parce que, comme pour les séries chronologiques, les données géoréférencées ont généralement une forte autocorrélation. Ainsi, la variation probable de pluviométrie entre deux stations peut, en première approximation, être considérée “dans les mêmes eaux” (si je puis dire) que les valeurs mesurées aux deux stations.
6.5.2 Interpolation avec DIP
Nous allons utiliser le package {gstat} pour interpoler la pluviométrie marocaine. Celui-ci propose plusieurs techniques d’interpolation. La méthode de la distance inversée pondérée (DIP, inverse weighted distance en anglais ou IDW) est une méthode simple. Elle calcule la moyenne pondérée par l’inverse de la distance entre le point à interpoler et les points de valeurs connues au voisinage. Le calcul se fait comme suit :
\[\hat{Z}(s_0) = \frac{\sum_{i=1}^n w(s_i) Z(s_i)}{\sum_{i=1}^n w(s_i)}\]
Cette équation est un calcul de moyenne, mais avec des poids variables \(w(s_i)\). L’astuce consiste à faire varier ces poids en fonction de la distance entre le point à interpoler \(Z(s_0)\) et les points connus \(Z(s_i)\). Dans le cas de DIP, c’est l’inverse de la distance \(d(s_0, s_i)\) exposant \(p\) qui est utilisée :
\[w(s_i) = \frac{1}{d(s_0, s_i)^p}\]
et la valeur par défaut de \(p\) est 2. Faire varier \(p\) permet d’avoir un effet d’autocorrélation qui se propage plus ou moins loin dans l’espace. Notez que cet effet est le même dans toutes les directions.
À vous de jouer !
Cette interpolation ne nécessite que les données mesurées de pluviométrie rain, donc, la formule correspondante est rain ~ 1 pour indiquer qu’à part une valeur moyenne de référence (l’équivalent de l’ordonnée à l’origine pour une régression linéaire), nous n’utiliserons pas d’autres variables prédictives. Le modèle se calcule comme suit :
Ensuite, nous effectuons une prédiction à l’aide de ce modèle en utilisant predict(). Par contre, les objets raster ne sont pas reconnus et nous devons travailler avec des objets stars. Donc, nous convertissons avec st_as_stars() du package {stars} qui est déjà chargé avec SciViews::R("spatial").
# [inverse distance weighted interpolation]# stars object with 2 dimensions and 2 attributes
# attribute(s):
# Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
# var1.pred 24.50199 168.9468 261.5684 246.3153 305.6972 959.1044 51067
# var1.var NA NA NA NaN NA NA 150400
# dimension(s):
# from to offset delta refsys x/y
# x 1 400 -17.3482 0.0416667 +proj=longlat +datum=WGS8... [x]
# y 1 376 36.1988 -0.0416667 +proj=longlat +datum=WGS8... [y]Le résultat est aussi un objet stars avec deux composantes :
var1.pred, les prédictionsvar1.var, la variance estimée (plus elle est grande en un point, plus la prédiction est incertaine)
Dans le cas de DIP, la variance n’est pas calculée (la colonne contient uniquement des NAs). Cet objet est utilisable par {tmap} directement. Nous pouvons en extraire une composante à l’aide de l’opérateur ["composante",,]. Donc, nous pouvons faire :
m_map + tm_shape(m_rain_idw["var1.pred",,]) +
tm_raster(n = 8, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - IDW") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)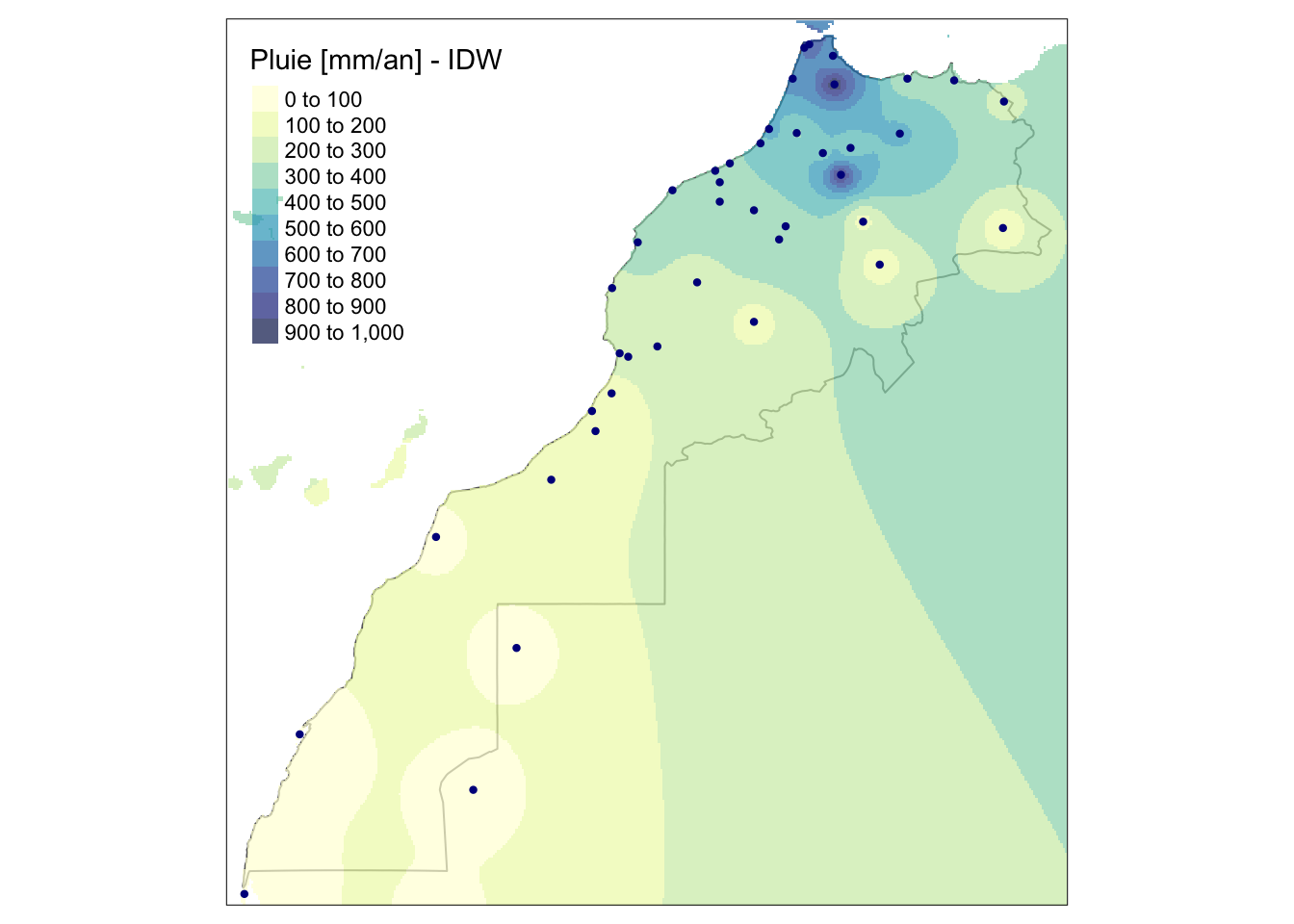
Le lissage moyenné avec propagation de l’effet sur une certaine distance donne une surface d’interpolation à la forme reconnaissable. Si nous modifions la valeur de \(p\), nous propageons plus ou moins loin l’effet. Avec \(p = 0.5\) cela donne :
m_g05 <- gstat(data = m_rain, formula = rain ~ 1, set = list(idp = .5))
m_pred05 <- predict(m_g05, newdata = st_as_stars(m_tm2))# [inverse distance weighted interpolation]m_map + tm_shape(m_pred05["var1.pred",,]) +
tm_raster(n = 8, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - IWD") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)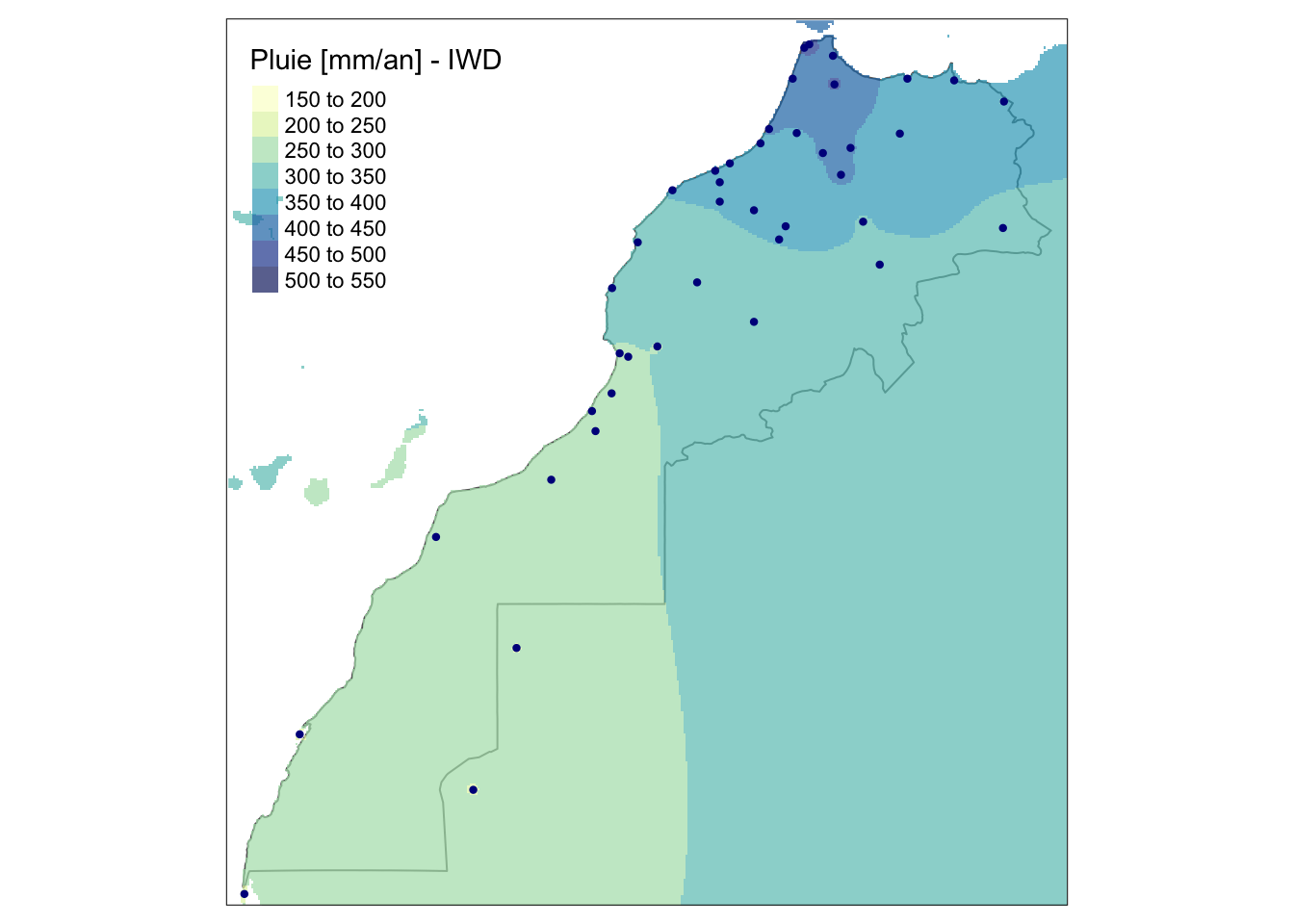
La propagation se fait à bien plus grande distance. Avec \(p = 10\), c’est l’inverse.
m_g10 <- gstat(data = m_rain, formula = rain ~ 1, set = list(idp = 10))
m_pred10 <- predict(m_g10, newdata = st_as_stars(m_tm2))# [inverse distance weighted interpolation]m_map + tm_shape(m_pred10["var1.pred",,]) +
tm_raster(n = 8, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - IWD") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)
À noter que les packages {sf}, {stars} et {raster} proposent toute une série de fonctions pour manipuler les différents objets. Voyez la documentation en ligne de ces packages, car cela sort du cadre de ce module. À titre d’illustration, nous allons restreindre le raster de prédiction de la pluviométrie à l’intérieur du territoire marocain uniquement à l’aide de st_crop() en utilisant comme premier argument les prédictions et comme second argument le polygone qui définit les frontières du pays m_bord.
m_rain_idw2 <- st_crop(m_rain_idw["var1.pred",,], m_bord)
# Le graphique montre bien le résultat de cette opération
m_map_idw <- m_map + tm_shape(m_rain_idw2) +
tm_raster(n = 8, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - IWD") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)
m_map_idw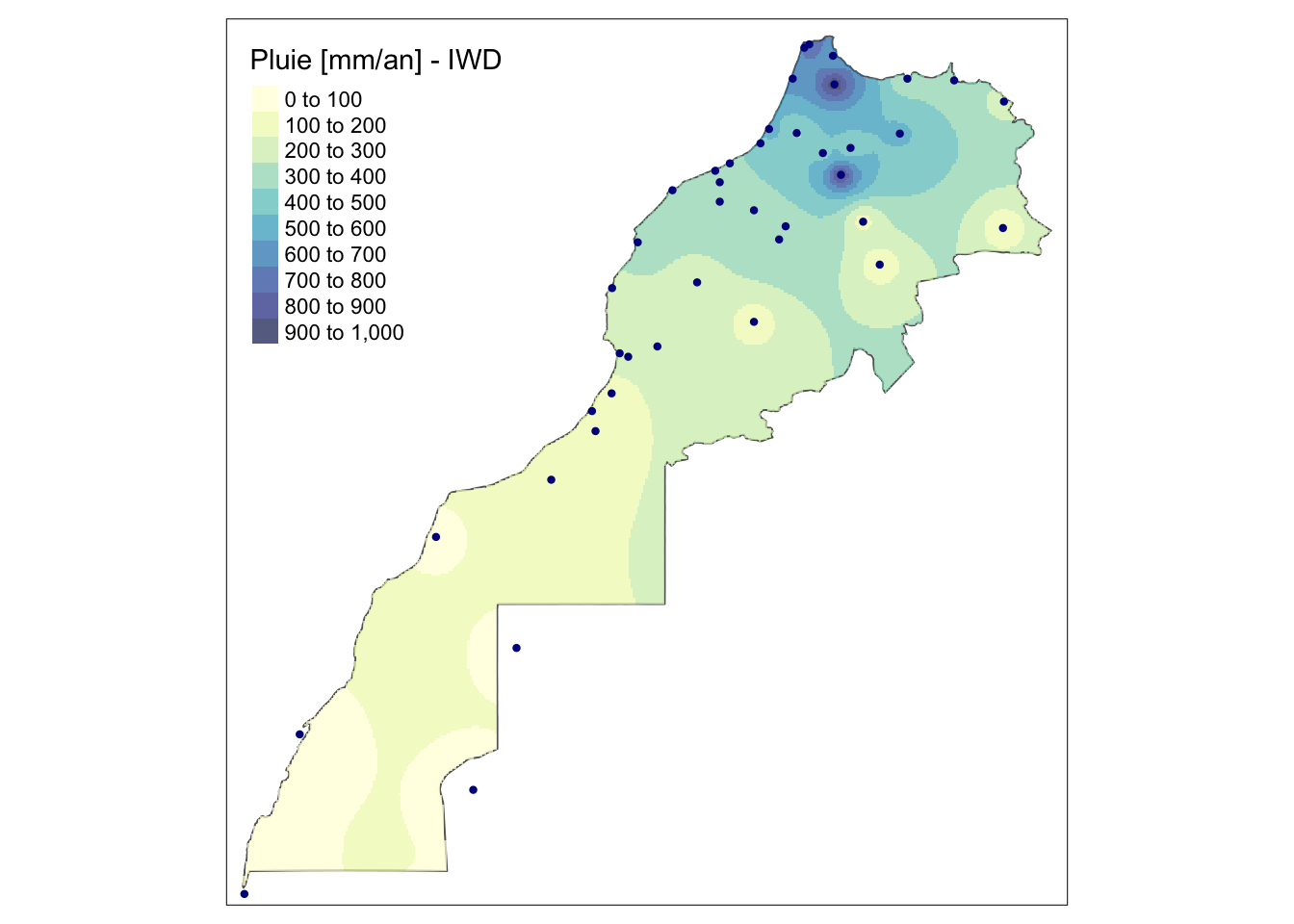
6.5.3 Krigeage ordinaire
Le krigeage est une technique d’interpolation qui utilise un modèle statistique (par comparaison, DIP est dit modèle déterministe) de l’effet en fonction de la distance au lieu d’utiliser une pondération fixée à l’avance. Cet effet peut même varier en fonction de la direction. Cette technique étant complexe, il faudrait pratiquement lui consacrer un cours entier. Aussi, nous ne ferons que nous sensibiliser à cette technique sans rentrer dans les détails.
À vous de jouer !
On appelle variogramme empirique la représentation de la demi-variance en fonction de la distance entre les points telle qu’observée sur base du réseau de points effectivement mesurés. Nous pouvons le calculer et le visionner à l’aide de variogram().
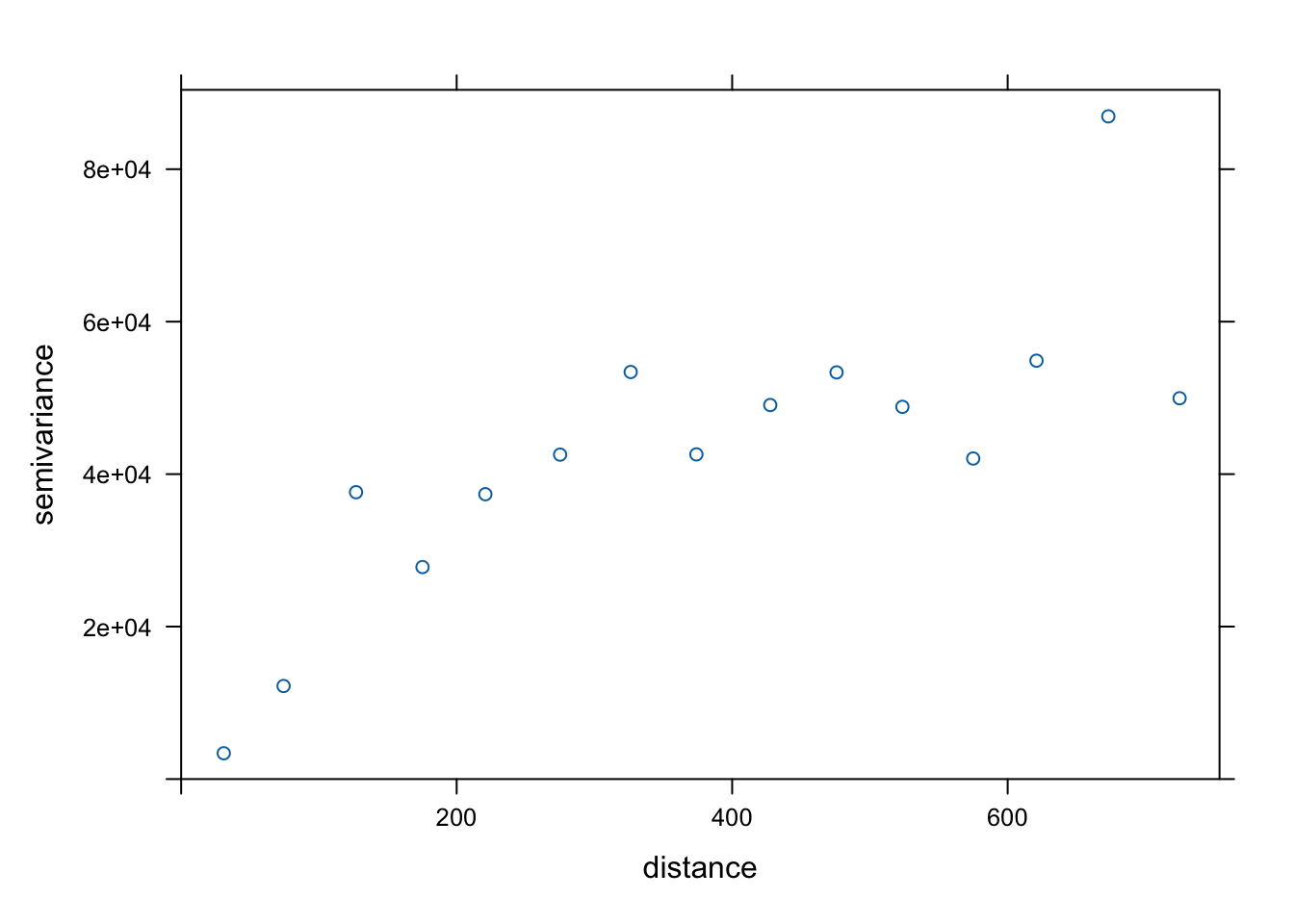
Le but ensuite est de trouver un modèle qui s’ajuste au mieux dans ce variogramme empirique. Nous avons plusieurs modèles différents utilisables. Le package {automap} propose la fonction autofitVariogram() qui détermine un modèle optimal automatiquement parmi une liste de modèles classiques. Par contre, les données doivent être converties encore en un autre objet (un SpatialPointsDataFrame, bienvenue dans l’écosystème divers et varié de R !) Donc, pour vous faciliter la vie, nous construisons la fonction auto_variogram() qui cache ces détails techniques.
auto_variogram <- function(data, formula, ...)
automap::autofitVariogram(formula, input_data = as(data, "Spatial"), ...)Cette fonction s’utilise alors simplement comme ceci :
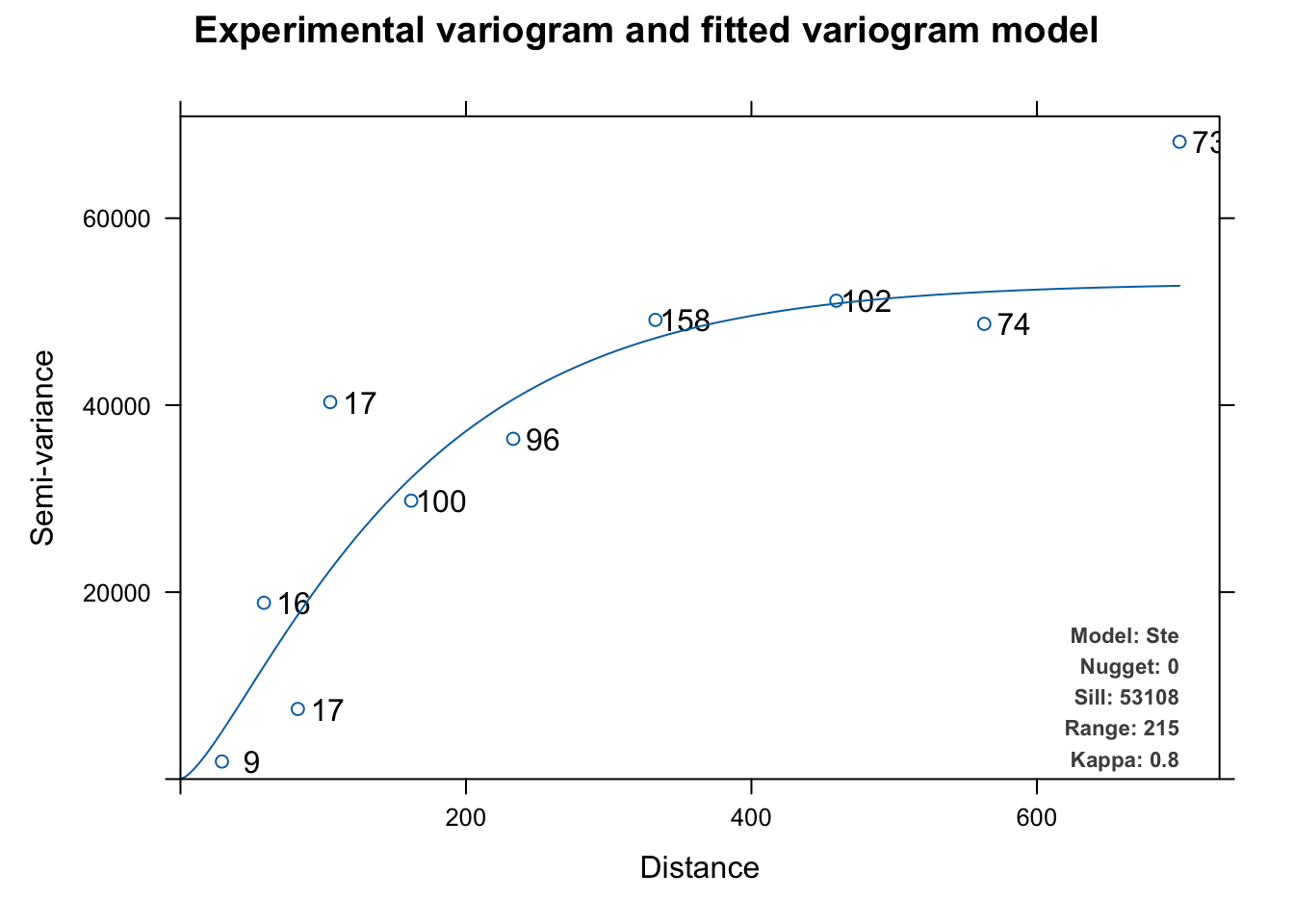
Ce modèle de variogramme (la courbe en bleue) est ensuite utilisé pour pondérer nos moyennes de façon similaire à DIP dans le krigeage ordinaire. En pratique, nous indiquons notre modèle à gstat() avec l’argument model=.
# Krigeage ordinaire
m_g_ko <- gstat(data = m_rain, formula = rain ~ 1, model = m_vario_ko$var_model)
# Calcul de la prédiction
m_pred_ko <- predict(m_g_ko, newdata = st_as_stars(m_tm2))# [using ordinary kriging]# Restriction du calcul à l'intérieur des frontières du pays
m_rain_ko <- st_crop(m_pred_ko["var1.pred",,], m_bord)
# Carte
m_map_ko <- m_map + tm_shape(m_rain_ko) +
tm_raster(n = 8, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - KrigO") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)
# Représentation côte à côte de IDW et krigeage ordinaire
tmap_arrange(m_map_idw, m_map_ko)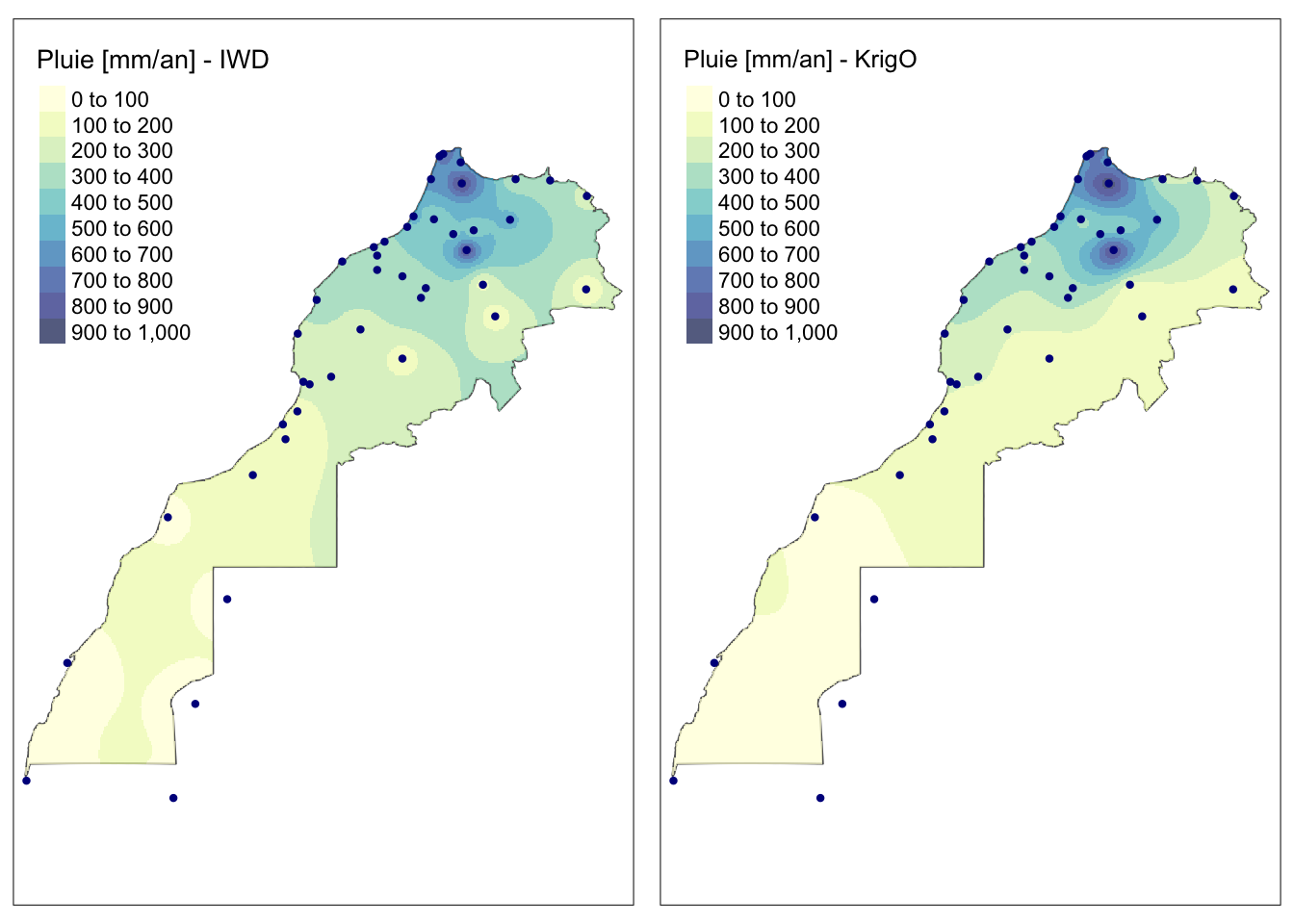
L’interpolation du krigeage à droite est meilleure que DIP à gauche, car nous n’avons plus cet effet de halo désagréable autour des points mesurés dans le désert.
6.5.4 Krigeage universel
Le krigeage ordinaire est ce qui se fait de mieux en matière d’interpolation spatiale si seule l’information relative à la variable à interpoler est disponible. Cependant, nous pouvons encore améliorer le travail si nous disposons de covariables mesurées avec une plus grande densité, à condition d’utiliser un modèle capable de les prendre en compte sous forme de variables indépendantes à la droite de la formule : le krigeage universel.
Effectivement ici, nous savons que le relief influence la pluviométrie qui est manifestement plus abondante dans la région montagneuse de l’Atlas. Or, il se fait que la pluie n’a pas été mesurée partout sur le relief, menant ainsi à des erreurs dans l’interpolation. Avec le krigeage universel, nous pouvons considérer le relief comme une covariable et tenter une meilleure prédiction de la pluie de cette façon-là.
Les covariables doivent être connues à la fois pour les points de la grille interpolée et pour les points mesurés. Nous devons donc ajouter l’information de l’altitude des stations météorologiques à m_rain avant de pouvoir procéder. Cette opération est appelée extraction de raster.
# [1] 71 173 118 59 9 1 282 23 473 10 520 67 63 512 1
# [16] 570 49 186 1441 18 373 783 72 511 466 1470 1565 1025 74 457
# [31] 21 69 263 1135 267 304 538 1 41 NA 442 29 409Nous voyons qu’une station n’est pas sur le modèle terrain (son élévation est NA). Nous l’éliminerons donc de nos données.
# Copie des données
m_rain2 <- m_rain
# Ajout de elevation
m_rain2$elevation <- extract(m_tm, m_rain2)
# Élimination des données manquantes
m_rain2 <- drop_na(m_rain2)
m_rain2# Simple feature collection with 42 features and 2 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -17.03 ymin: 20.93 xmax: -1.93 ymax: 35.78
# Geodetic CRS: +proj=longlat +datum=WGS84
# First 10 features:
# rain elevation geometry
# 1 57.3 71 POINT (-13.22 27.17)
# 2 138.5 173 POINT (-10.12 29.37)
# 3 29.4 118 POINT (-15.93 23.72)
# 4 818.7 59 POINT (-5.8 35.78)
# 5 682.4 9 POINT (-5.9 35.72)
# 6 653.2 1 POINT (-6.13 35.18)
# 7 961.4 282 POINT (-5.3 35.08)
# 8 299.3 23 POINT (-3.85 35.18)
# 9 261.8 473 POINT (-1.93 34.78)
# 10 541.1 10 POINT (-6.6 34.3)Nous pouvons maintenant explorer un krigeage universel avec le modèle terrain comme covariable. La formule rain ~ 1du krigeage ordinaire est donc remplacée ici par rain ~ elevation.

Effectuons maintenant notre krigeage.
# Krigeage universel avec elevation comme covariable
m_g_ku <- gstat(data = m_rain2, formula = rain ~ elevation,
model = m_vario_ku$var_model)
# Calcul de la prédiction : il faut la covariable, donc on la renomme d'abord
m_tm_stars2 <- st_as_stars(m_tm2)
names(m_tm_stars2) <- "elevation"
m_pred_ku <- predict(m_g_ku, newdata = m_tm_stars2)# [using universal kriging]# Restriction du calcul à l'intérieur des frontières du pays
m_rain_ku <- st_crop(m_pred_ku["var1.pred",,], m_bord)
# Carte
m_map_ku <- m_map + tm_shape(m_rain_ku) +
tm_raster(n = 9, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - KrigU") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)
# Représentation côte à côte de IDW et krigeage universel
tmap_arrange(m_map_ko, m_map_ku)
Avec le krigeage universel, à droite, nous voyons maintenant clairement l’effet du relief sur l’interpolation de la pluviométrie. Notez aussi que notre krigeage a évalué des pluies encore plus fortes que les valeurs maximales réellement observées, parce qu’il a déterminé que la pluie augmente avec l’altitude et que des points plus élevés que la plus haute station météorologique existent.
Est-ce que l’interpolation de droite est parfaite ? Disons qu’elle est meilleure, mais pas encore ce qui se fait de mieux. En effet, deux phénomènes bien connus n’ont pas pu être pris en compte ici :
Les deux flancs de montagnes ne sont pas égaux en termes de pluviométrie. Celui exposé vers la mer reçoit les masses d’airs humides et donc les pluies, alors que l’autre versant montagneux est plus sec.
La distance à la mer joue un rôle également dans la pluviométrie locale.
Les météorologues ont mis au point des techniques très sophistiquées pour ternir compte de ces critères, notamment la méthode AURELHY. Cependant, cette dernière technique est très difficile à mettre en œuvre et a de nombreux paramètres. Nous vous conseillons donc de rechercher plutôt un krigeage optimal de vos données et de vous perfectionner avec cette technique avant d’attaquer un niveau supérieur. Nous vous démontrons juste ci-dessous, à titre facultatif, ce que cela donne.
6.5.5 Interpolation avec AURELHY
Cette section est facultative.
La méthode AURELHY tient compte du relief de manière asymétrique en fonction du versant et d’autres variables comme la distance à la mer pour les interpolations de données hydrométéorologiques. Pour le biologiste, une estimation correcte des conditions météorologiques sur son site est souvent indispensable. Mais cette technique peut aussi lui être utile à chaque fois qu’il s’intéresse à des données étroitement dépendantes de la pluviométrie, comme les communautés végétales, ou la production de champs cultivés, par exemple.
Dans R, le package {aurelhy} fait ce type d’interpolation. Nous chargeons donc ce package. Nous utilisons aussi un masque qui indique la zone à interpoler (mmask) et des données complémentaires qui ont été précalculées de distance à la mer dans mseadist. Nous travaillons aussi avec les objets geomat, geoshapes et geopoints propres à {aurelhy}.
#
# Attaching package: 'aurelhy'# The following object is masked from 'package:raster':
#
# resample# The following object is masked from 'package:terra':
#
# resamplemseadist <- read("mseadist", package = "aurelhy")
mmask <- read("mmask", package = "aurelhy")
# S'assurer que toutes les stations sont reprises dans le masque
mmask2 <- add.points(mmask, mrain)À présent, nous interpolons les données de pluviométrie à l’aide de la méthode AURELHY. Les nombreux paramètres de aurelhy() sont décrits dans l’aide de la fonction (leur description sort du cadre de cette simple démo).
m_aurelhy <- aurelhy(morocco, mmask2, auremask(), x0 = 30, y0 = 54, step = 12,
scale = FALSE, nbr.pc = 10, vgmodel = gstat::vgm(100, "Gau", 1, 1),
add.vars = mseadist, var.name = "seadist")Cet objet m_aurelhy peut ensuite être utilisé pour prédire la pluviométrie (que nous passons temporairement en échelle logarithmique).
# [adjusted R-squared is 0.955]
# [using universal kriging]#
# Call:
# lm(formula = model, data = pred)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.128206 -0.024055 -0.000544 0.036791 0.126678
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -3.928e+00 6.321e-01 -6.214 2.02e-06 ***
# x -7.158e-02 1.687e-02 -4.243 0.000284 ***
# y 1.783e-01 1.533e-02 11.628 2.39e-11 ***
# z 2.423e-04 1.152e-04 2.104 0.046041 *
# PC1 6.930e-05 3.393e-05 2.042 0.052251 .
# PC2 5.381e-05 3.353e-05 1.605 0.121625
# PC3 -1.687e-04 5.239e-05 -3.220 0.003662 **
# PC4 1.156e-04 5.917e-05 1.954 0.062441 .
# PC5 4.804e-05 1.051e-04 0.457 0.651879
# PC6 -1.489e-04 8.895e-05 -1.673 0.107219
# PC7 3.419e-04 1.345e-04 2.542 0.017876 *
# PC8 3.769e-04 1.077e-04 3.500 0.001844 **
# PC9 1.590e-04 1.682e-04 0.945 0.354086
# PC10 5.754e-05 2.175e-04 0.265 0.793599
# seadist -6.232e-04 4.130e-04 -1.509 0.144391
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.06886 on 24 degrees of freedom
# Multiple R-squared: 0.9714, Adjusted R-squared: 0.9547
# F-statistic: 58.23 on 14 and 24 DF, p-value: 4.733e-15Nous voyons que quelques variables de ce modèle sont très significatives. Une étape du calcul consiste à réaliser une ACP sur les données, d’où les variables PC1 à PC10 qui en sont les axes principaux. La variable z est l’élévation. Une fois que nous sommes satisfaits du résultat, nous transformons la variable prédite en objet geomat, et ensuite en objet raster pour le cartographier.
Comme il se peut que l’interpolation ait donné des valeurs très élevées ou très basses en quelques points, nous allons niveler un peu tout cela vers une plage de valeurs effectivement observées.
# [1] 4.123362 3440.555674# [1] 24.5 961.4Nous atteignons près de 3500mm/an de pluie en certains endroits, ce qui est énorme. Combien de pixels sont concernés ?
# [1] 34Seulement quelques dizaines. Ceci est probablement lié au manque de stations pluviométriques en altitude. Nous limitons les valeurs à 1200mm/an maximum, et ensuite, nous transformons en objet raster.
# class : RasterLayer
# dimensions : 150, 160, 24000 (nrow, ncol, ncell)
# resolution : 0.1, 0.1 (x, y)
# extent : -17.05241, -1.052414, 20.94464, 35.94464 (xmin, xmax, ymin, ymax)
# crs : +proj=longlat +datum=WGS84
# source : memory
# names : layer
# values : 4.123362, 1200 (min, max)Enfin, nous réalisons une carte de la pluviométrie que nous plaçons côte à côte avec le krigeage universel tenant compte du relief pour comparaison à l’aide de tm_arrange().
m_map_rain <- m_map + tm_shape(rain_ras) +
tm_raster(n = 10, alpha = 0.7, palette = "YlGnBu",
title = "Pluie [mm/an] - AURELHY") +
tm_layout(legend.position = c("left", "top")) +
tm_shape(m_rain) + tm_dots(col = "darkblue", size = 0.05)
# Deux cartes côte à côte
tmap_arrange(m_map_ku, m_map_rain)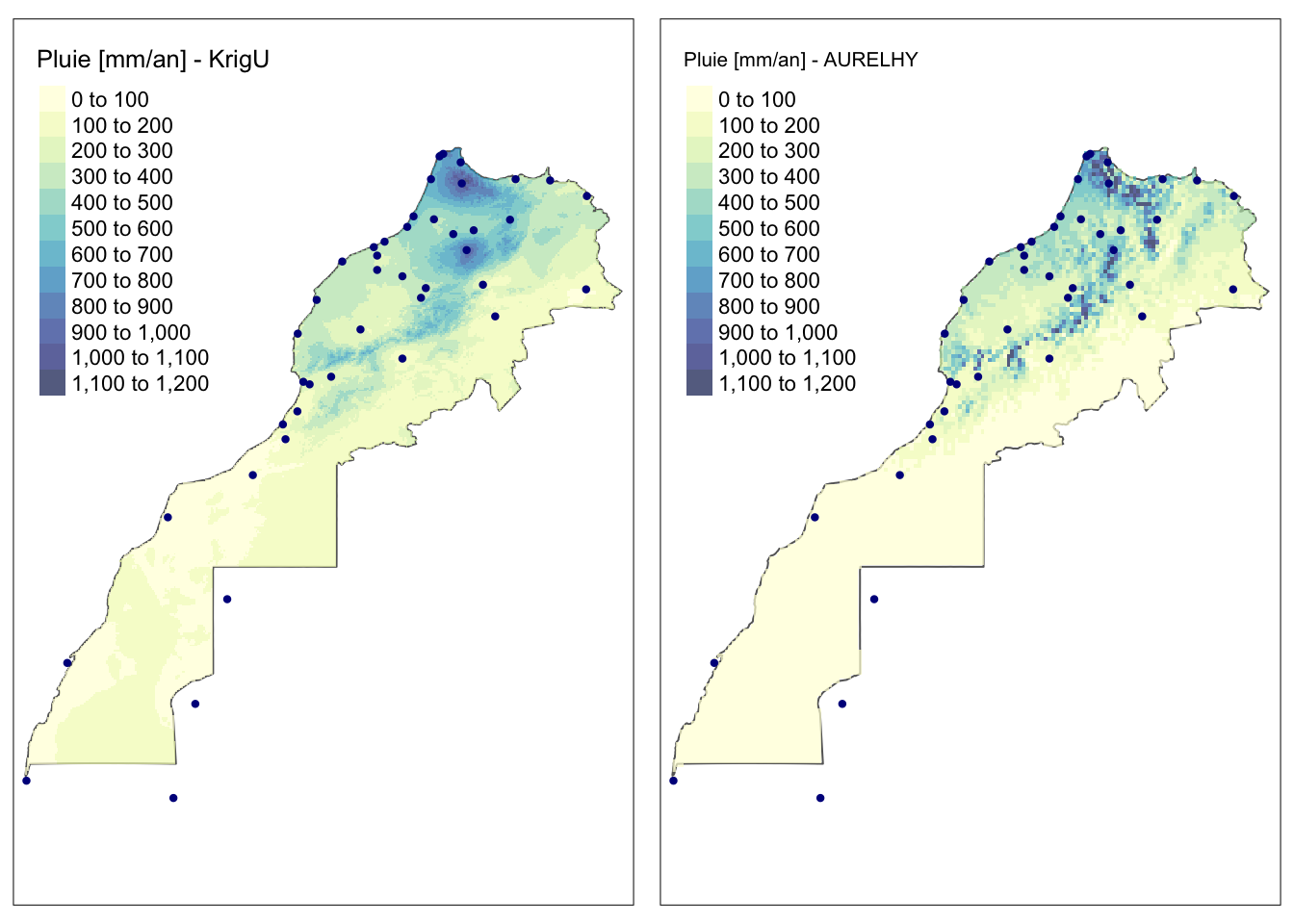
Nous avons deux interpolations assez semblables, mais le krigeage donne une estimation un peu plus diffuse, là où AURELHY utilise réellement le relief très escarpé de l’Atlas pour prédire des pluies très contrastées sur des distances faibles. Terminons ceci en beauté avec une comparaison du relief et des pluies observées à gauche avec le résultat issu d’AURELHY à droite.
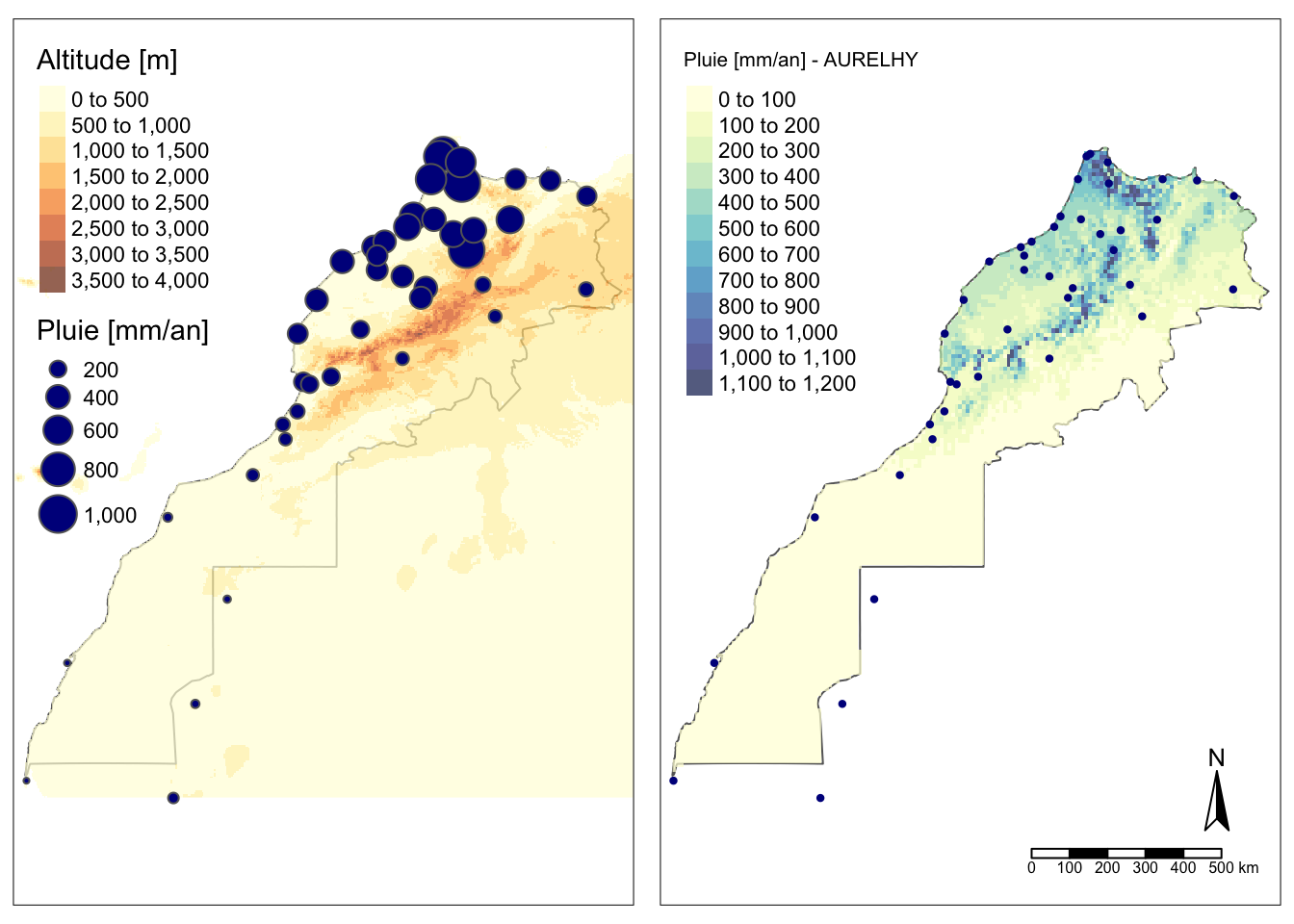
À vous de jouer !
Réalisez en groupe le travail C06Ga_map.
Travail en groupe de 2 pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2023-12-22 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.
Pour en savoir plus
Intro to GIS and Spatial Analysis est un ouvrage complet qui introduit toute la matière de manière claire, mais qui montre aussi comment l’implémenter dans R (en anglais).
Geocomputation with R présente certains aspects complémentaires au précédent ouvrage (en anglais). Il montre, par exemple, comment combiner les capacités géostatistique et d’apprentissage machine dans R pour étudier des modèles spatialisés potentiellement très puissants. Des applications pratiques dans différentes disciplines (dont l’écologie) mettent tout cela en musique.
Geospatial Health Data: modeling and visualization with R-INLA and Shiny insiste particulièrement sur les cartes interactives et les applications Shiny (dashboard) pour présenter des données et modèles géospatialisés de manière vivante et interactive (en anglais).
Spatial Data Science with R en anglais développe tout un chapitre consacré à la modélisation de la distribution des espèces.
CRAN Task View: Analysis of Spatial Data, en anglais. Répertorie tous les packages de CRAN (le site officiel de distribution de packages R additionnels) qui traitent des statistiques spatiales et de la cartographie.
Chapitre consacré aux données spatiales de “Data Science with R: A resource compendium”, en anglais. Un document qui oriente dans l’écosystème riche des packages R.