2.1 Validation croisée
Rappelez-vous qu’une règle à laquelle il ne faut jamais déroger, c’est de ne pas utiliser les mêmes individus en apprentissage et en test.
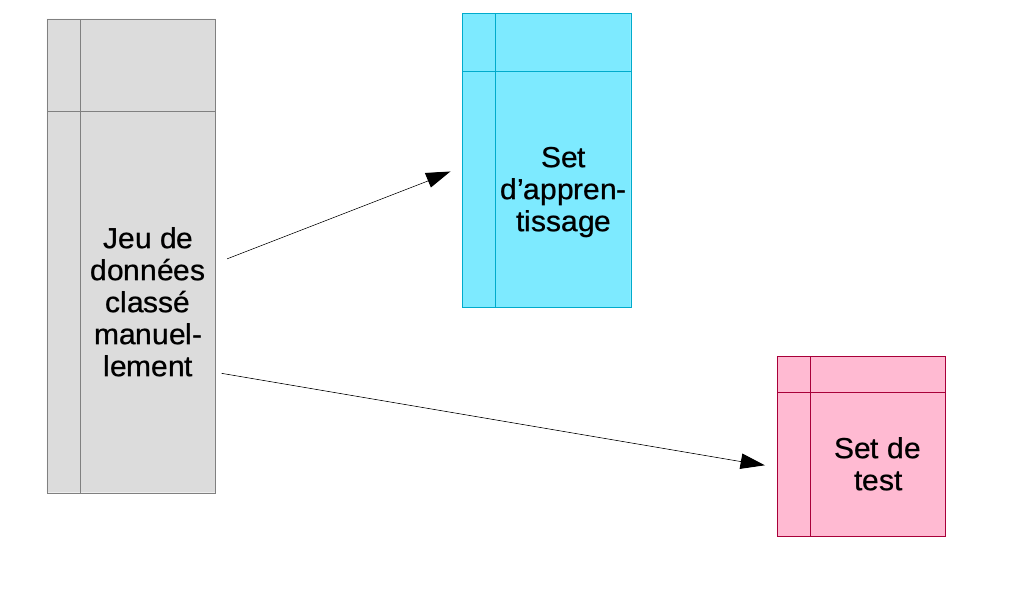
Souvent, la grosse difficulté est d’obtenir suffisamment d’objets de chaque classe identifiés manuellement pour permettre à la fois l’apprentissage et le test. Un test sur les mêmes objets que ceux utilisés lors de l’apprentissage mène à une surestimation systématique des performances du classifieur. Nous sommes donc contraints d’utiliser des objets différents dans les deux cas. Naturellement, plus, nous avons d’objets dans le set d’apprentissage et dans le set de test, et meilleur sera notre classifieur et notre évaluation de son efficacité.
La validation croisée permet de résoudre ce dilemme en utilisant en fin de compte tous les objets, à la fois dans le set d’apprentissage et dans le set de test, mais jamais simultanément. L’astuce consiste à diviser aléatoirement l’échantillon en n sous-ensembles à peu près égaux en effectifs. Ensuite, l’apprentissage suivi du test est effectué n fois indépendamment. À chaque fois, on sélectionne tous les sous-ensembles sauf un pour l’apprentissage, et le sous-ensemble laissé de côté est utilisé pour le test. L’opération est répétée de façon à ce que chaque sous-ensemble serve de set de test tour à tour. Au final, on rassemble les résultats obtenus sur les n sets de tests, donc, sur tous les objets de notre échantillon et on calcule la matrice de confusion complète en regroupant donc les résultats des n étapes indépendantes. Enfin, on calcule les métriques souhaitées sur cette matrice de confusion afin d’obtenir une évaluation approchée et non biaisée des performances du classifieur complet (entraîné sur l’ensemble des données à disposition). L’animation suivante visualise le processus pour que cela soit plus clair dans votre esprit.
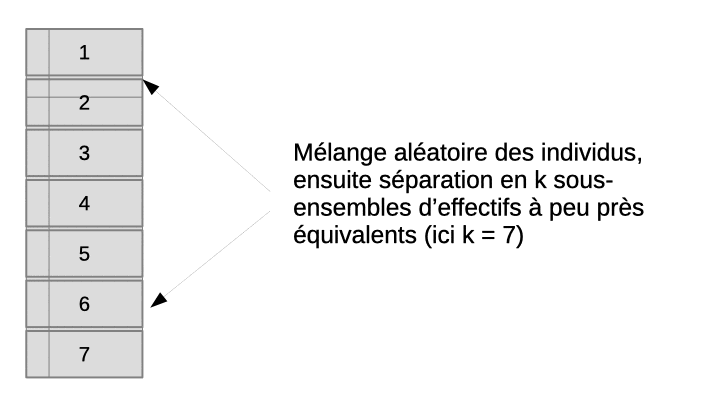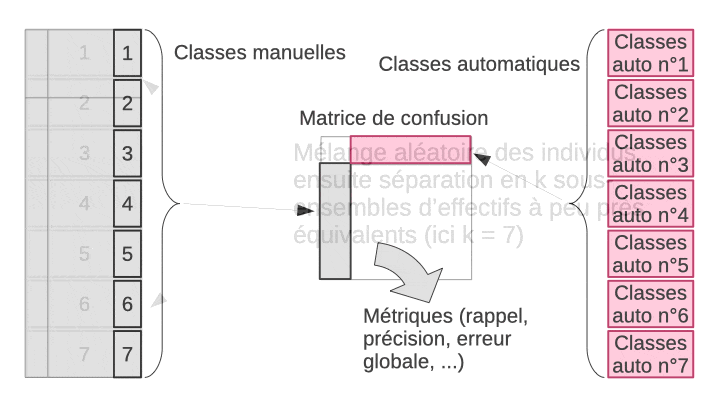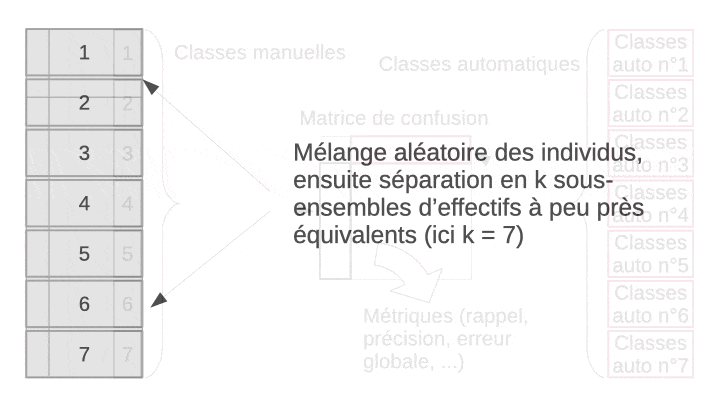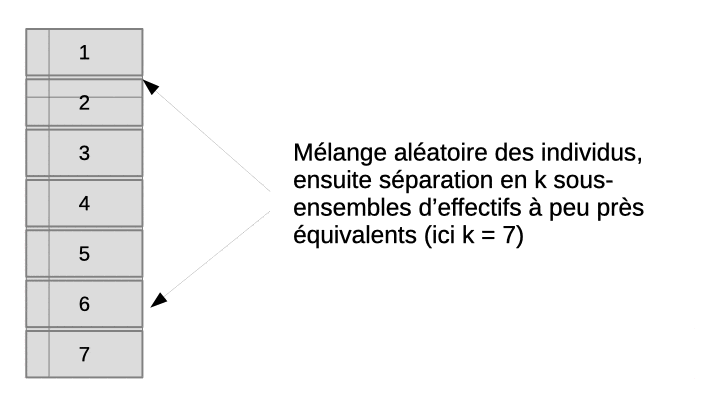
À vous de jouer !
Au final, nous aurons utilisé tous les individus à la fois en apprentissage et en test, mais jamais simultanément. Le rassemblement des prédictions obtenues à chaque étape nous permet d’obtenir une grosse matrice de confusion qui contient le même nombre d’individus que l’ensemble de notre jeu de données initial. Naturellement, nous n’avons pas le même classifieur à chaque étape, et celui-ci n’est pas aussi bien construit que s’il utilisait véritablement toutes les observations. Mais plus le découpage est fin et plus nous nous en approchons. À la limite, pour n observations, nous pourrions réaliser k = n sous-ensembles, c’est-à-dire que chaque sous-ensemble contient un et un seul individu. Nous avons alors à chaque fois le classifieur le plus proche possible de celui que l’on obtiendrait avec véritablement toutes les observations puisqu’à chaque étape nous ne perdons qu’un seul individu en phase d’apprentissage. La contrepartie est un temps de calcul potentiellement très, très long puisqu’il y a énormément d’étapes. Cette technique porte le nom de validation par exclusion d’une donnée ou leave-one-out cross-validation en anglais, LOOCV en abrégé. À l’autre extrême, nous pourrions utiliser k = 2. Mais dans ce cas, nous n’utilisons que la moitié des observations en phase d’apprentissage à chaque étape. C’est le plus rapide, mais le moins exact.
À vous de jouer !
En pratique, un compromis entre exactitude et temps de calcul nous mène à choisir souvent la validation croisée dix fois (ten-fold cross-validation en anglais). Nous divisons aléatoirement en dix sous-ensembles d’à peu près le même nombre d’individus et nous répétons donc l’opération apprentissage -> test seulement dix fois. Chacun des dix classifieurs a donc été élaboré avec 90% des données totales, ce qui représente souvent un compromis encore acceptable pour estimer les propriétés qu’aurait le classifieur réalisé avec 100% des données. Toutefois, si nous constatons que le temps de calcul est raisonnable, rien ne nous empêche d’augmenter le nombre de sous-ensembles, voire d’utiliser la version par exclusion d’une donnée, mais en pratique nous observons tout de même que cela n’est pas raisonnable sur de très gros jeux de données et avec les algorithmes les plus puissants, mais aussi les plus gourmands en temps de calcul comme la forêt aléatoire ou les réseaux de neurones que nous aborderons dans le prochain module.
2.1.1 Application sur les manchots
Appliquons cela tout de suite avec l’ADL sur nos manchots. Plus besoin de séparer le jeu de données en set d’apprentissage et de test indépendants. La fonction cvpredict(, cv.k = ...) va se charger de ce partitionnement selon l’approche décrite ci-dessus en cv.k étapes. Notre analyse s’écrit alors :
# Importation et remaniement des données comme précédemment
read("penguins", package = "palmerpenguins") %>.%
rename(.,
bill_length = bill_length_mm,
bill_depth = bill_depth_mm,
flipper_length = flipper_length_mm,
body_mass = body_mass_g) %>.%
select(., -year, -island, -sex) %>.%
drop_na(.) %->%
penguinsUne fois notre tableau complet, correctement nettoyé et préparé, nous faisons :
# ADL avec toutes les données
penguins_lda <- mlLda(data = penguins, species ~ .)
# Prédiction par validation croisée 10x
set.seed(7567) # Pensez à varier le nombre à chaque fois ici !
penguins_pred <- cvpredict(penguins_lda, cv.k = 10)
# Matrice de confusion
penguins_conf <- confusion(penguins_pred, penguins$species)
plot(penguins_conf)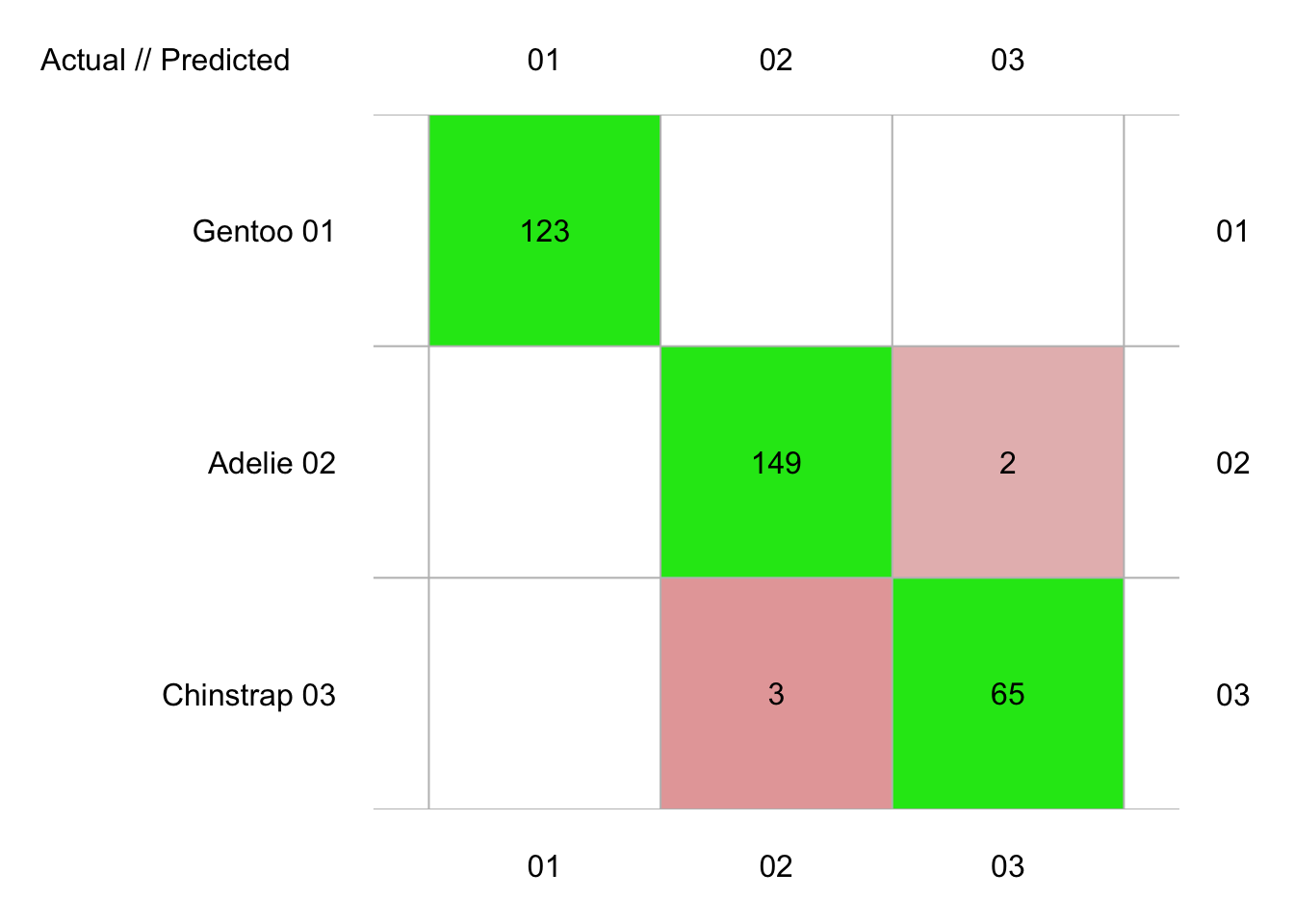
Ici, nous avons cinq erreurs, mais attention, ceci est comptabilisé sur trois fois plus de données que précédemment, puisque l’ensemble du jeu de données a servi ici en test, contre un tiers seulement auparavant. Donc, notre estimation des performances du classifieur est assez comparable, avec une parfaite séparation de “Gentoo”, mais une petite erreur entre “Chinstrap” et “Adelie”. Les métriques sont disponibles à partir de notre objet penguins_conf comme d’habitude :
# 342 items classified with 337 true positives (error = 1.5%)
#
# Global statistics on reweighted data:
# Error rate: 1.5%, F(micro-average): 0.982, F(macro-average): 0.982
#
# # A data.frame: 3 x 24
# ` ` Fscore Recall Precision Specificity NPV FPR FNR FDR FOR
# <rowna> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 Gentoo… 1 1 1 1 1 0 0 0 0
# 2 Adelie… 0.983 0.987 0.980 0.984 0.989 0.0157 0.0132 0.0197 0.0105
# 3 Chinst… 0.963 0.956 0.970 0.993 0.989 0.00730 0.0441 0.0299 0.0109
# # … with 15 more variables: LRPT <dbl>, LRNT <dbl>, LRPS <dbl>, LRNS <dbl>,
# # BalAcc <dbl>, MCC <dbl>, Chisq <dbl>, Bray <dbl>, Auto <dbl>, Manu <dbl>,
# # A_M <dbl>, TP <int>, FP <dbl>, FN <dbl>, TN <dbl>Notez cependant ici que vous ne devez pas vous contenter de générer et imprimer le tableau contenant toutes les métriques. En fonction de votre objectif, vous choisissez les métriques les plus pertinentes en les indiquant dans l’argument type= de summary() dans l’ordre que vous voulez. L’argument sort.by= permet, en outre, de trier les lignes de la meilleure à la moins bonne valeur pour une métrique donnée. Par exemple, si nous ne voulons que “Recall”, “Precision” et “Fscore” dans cet ordre, en triant par “Recall”, nous ferons :
# 342 items classified with 337 true positives (error = 1.5%)
#
# Global statistics on reweighted data:
# Error rate: 1.5%, F(micro-average): 0.982, F(macro-average): 0.982
#
# # A data.frame: 3 x 3
# ` ` Recall Precision Fscore
# <rownames> <dbl> <dbl> <dbl>
# 1 Gentoo 1 1 1
# 2 Adelie 0.987 0.980 0.983
# 3 Chinstrap 0.956 0.970 0.963Précédemment, nous avions 1,8% d’erreur, et maintenant, nous n’en avons plus que 1,5%. C’est normal que notre taux d’erreur baisse un petit peu, car nos classifieurs par validation croisée utilisent 90% des données alors qu’auparavant, nous n’en utilisions que les 2/3. Les performances de nos classifieurs s’améliorent avec l’augmentation des données jusqu’à atteindre un palier. Il faut essayer de l’atteindre en pratique : s’il est possible d’ajouter plus de données, nous comparons avant-après, et si les performances s’améliorent, nous ajoutons encore plus de données jusqu’à atteindre le palier. Notez aussi que la quantité de données nécessaires dépend également de l’algorithme de classification. En général, plus il est complexe, plus il faudra de données. Pensez-y si vous en avez peu et utilisez alors préférentiellement des algorithmes plus simples comme ADL dans ce cas.
Si nous voulons faire un “leave-one-out”, nous ferions (sachant que nos données comptent 342 cas, nous indiquons ici cv.k = 342) :
penguins_pred_loo <- cvpredict(penguins_lda, cv.k = 342)
# Matrice de confusion
penguins_conf_loo <- confusion(penguins_pred_loo, penguins$species)
plot(penguins_conf_loo)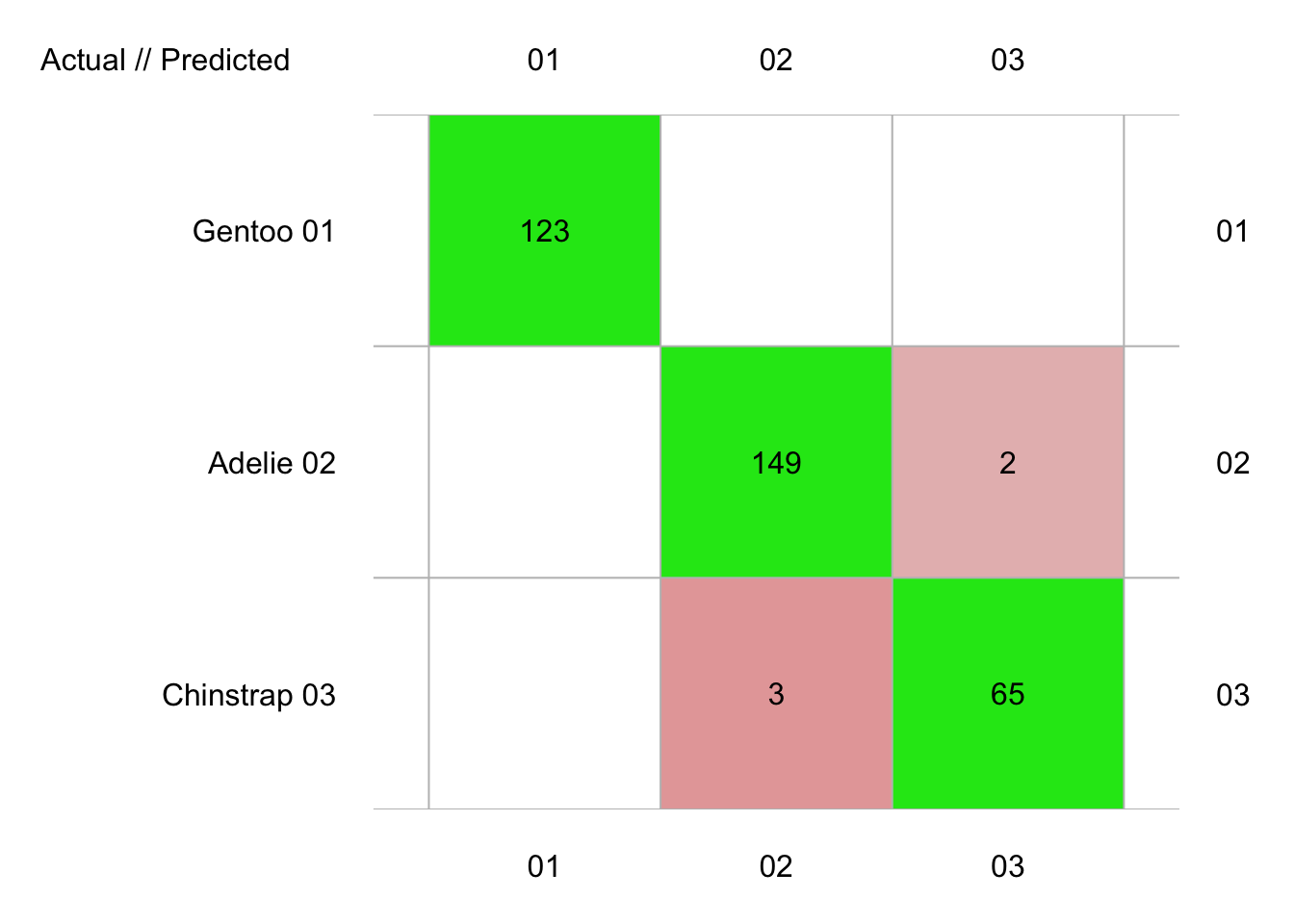
# 342 items classified with 337 true positives (error = 1.5%)
#
# Global statistics on reweighted data:
# Error rate: 1.5%, F(micro-average): 0.982, F(macro-average): 0.982
#
# # A data.frame: 3 x 3
# ` ` Recall Precision Fscore
# <rownames> <dbl> <dbl> <dbl>
# 1 Gentoo 1 1 1
# 2 Adelie 0.987 0.980 0.983
# 3 Chinstrap 0.956 0.970 0.963Le résultat est le même. Donc, nous venons de montrer que, dans le cas de ce jeu de données et de l’ADL, une validation croisée dix fois permet d’estimer les performances du classifieur aussi bien que l’approche bien plus coûteuse en calculs (342 classifieurs sont calculés et testés) du “leave-one-out”.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel C02La_cv (Validation croisée).
BioDataScience3::run("C02La_cv")À retenir
Bien que plus complexe en interne, la validation croisée est très facile à utiliser avec {mlearning} grâce à la fonction
cvpredict(),L’approche par validation croisée optimise l’utilisation des données à disposition. C’est la technique à préférer, sauf si nous disposons vraiment de données à profusion.