5.2 Filtrage d’une série
Le filtrage d’une série consiste à remplacer chaque valeur de cette série par une combinaison de ses diverses valeurs. Lorsque le filtre conduit à réduire la variance en éliminant notamment les très hautes fréquences, on parle aussi de lissage du signal (smoothing en anglais). Nous allons à présent aborder quelques techniques de filtrage et découvrir dans quelles situations elles sont utiles.
5.2.1 Moyennes mobiles
Le principe d’une fenêtre mobile consiste à balader une fenêtre de taille définie dans la série, centrée sur une observation \(X_t\), et de remplacer cette observation par le résultat du calcul dans la fenêtre. Ensuite, la fenêtre coulisse d’une observation vers la droite et est donc centrée sur l’observation \(X_{t+1}\). À nouveau, un calcul est appliqué sur les valeurs contenues dans le fenêtre, et le résultat du calcul remplace cette observation \(X_{t+1}\), et ainsi de suite jusqu’à ce que toutes les observations de la série sont remplacées.
La taille de la fenêtre est définie par un paramètre k qui s’appelle l’ordre de la fenêtre mobile, correspondant au nombre d’observations comprises de part et d’autre de \(X_t\) dans la fenêtre. Le nombre d’observations à l’intérieur de la fenêtre est donc de 2 k + 1 (k observations à gauche de \(X_t\), \(X_t\) lui-même et k observations à droite). Pour k = 2, chaque observation est donc remplacée par un calcul réalisé sur cinq observations successives.
Un problème se pose aux deux extrémités, car la fenêtre dépasse de la série et des valeurs manquantes apparaissent. Il est possible de dupliquer les valeurs extrêmes pour remplir ces trous, de faire le calcul en éliminant ces valeurs manquantes, voire encore d’autres stratégies. Mais à tous les coups, ces artifices généreront des effets indésirables aux deux extrémités : les effets de bord. Il est aussi possible de raccourcir la série aux deux extrémités pour éluder la question tout simplement.
Dans le cas de la moyenne mobile (moving average en anglais), le calcul qui est réalisé à l’intérieur de la fenêtre est bien sûr la moyenne des observations qu’elle contient. Pour reprendre notre exemple avec k = 2, si nous appelons \(M_t\) la moyenne mobile calculée qui remplace \(X_t\) dans la série filtrée, nous aurons :
\[M_t = \frac{X_{t-2} + X_{t-1} + X_t + X_{t+1} + X_{t+2}}{5}\] et pour l’observation suivante :
\[M_{t+1} = \frac{X_{t-1} + X_{t} + X_{t+1} + X_{t+2} + X_{t+3}}{5}\]
Et ainsi de suite… Cela se généralise bien sûr pour n’importe quelle valeur de k :
\[M_{t=i} = \sum_{j = -k}^k \frac{X_{t=i+j}}{2k + 1}\]
Nous avons donné le même poids à chaque observation dans la fenêtre qui compte donc pour 1/5 chacune dans le cas k = 2. Dans ce cas, nous parlerons d’une moyenne mobile simple. Il est cependant possible de faire varier également les pondérations à l’intérieur de la fenêtre, mais nous n’utiliserons pas cette dernière variance ici.
5.2.1.1 Propriétés
Le filtrage effectue un lissage de la série, et la bande de lissage est égale à la largeur de la fenêtre, donc 2 k + 1. Cela signifie que cette technique de filtrage a la propriété d’éliminer les signaux cycliques de fréquence égale à la bande de lissage. Par exemple, pour des données mensuelles, nous pouvons éliminer l’effet saisonnier (on parle de désaisonnalisation) en utilisant une moyenne mobile de taille de fenêtre proche. Comme la taille doit être impaire, on choisira k = 6, ce qui donne une bande de lissage de 13 mois, pas trop éloignée des 12 mois visés.
Pour un effet accru, il est possible d’effectuer successivement plusieurs lissages par moyenne mobile. C’est l’argument times= qui contrôle cela dans decaverage() et tsd(method = "average"). À noter, enfin, que les cycles de fréquence égale à la bande de lissage ne sont pas les seuls à être éliminés. D’autres fréquences sont également affectées à des degrés divers. Par exemple pour une désaisonnalisation, les fréquences 6, 4, 3, 12/5 et 2 mois sont également impactées à des degrés divers. Comprenez ici que le filtre n’a pas un comportement parfait et que des artéfacts apparaissent, du moins si on se limite à considérer que la moyenne mobile n’élimine que le cycle de fréquence égale à la bande de lissage !
Un autre phénomène qu’il faut connaître est l’effet Slusky-Yule. L’application d’un filtrage par moyenne mobile engendre une oscillation artificielle dont la période dépend à la fois de l’ordre de la fenêtre du lissage et de l’autocorrélation présente dans la série. Cette période peut se calculer (nous vous renvoyons au manuel de {pastecs} pour les détails de ce calcul).
Exemple
Nous avons déjà réalisé une désaisonnalisation sur co2 précédemment dans ce module. Voyons à présent comment ce filtre se comporte sur un signal cyclique complexe comme lynx.
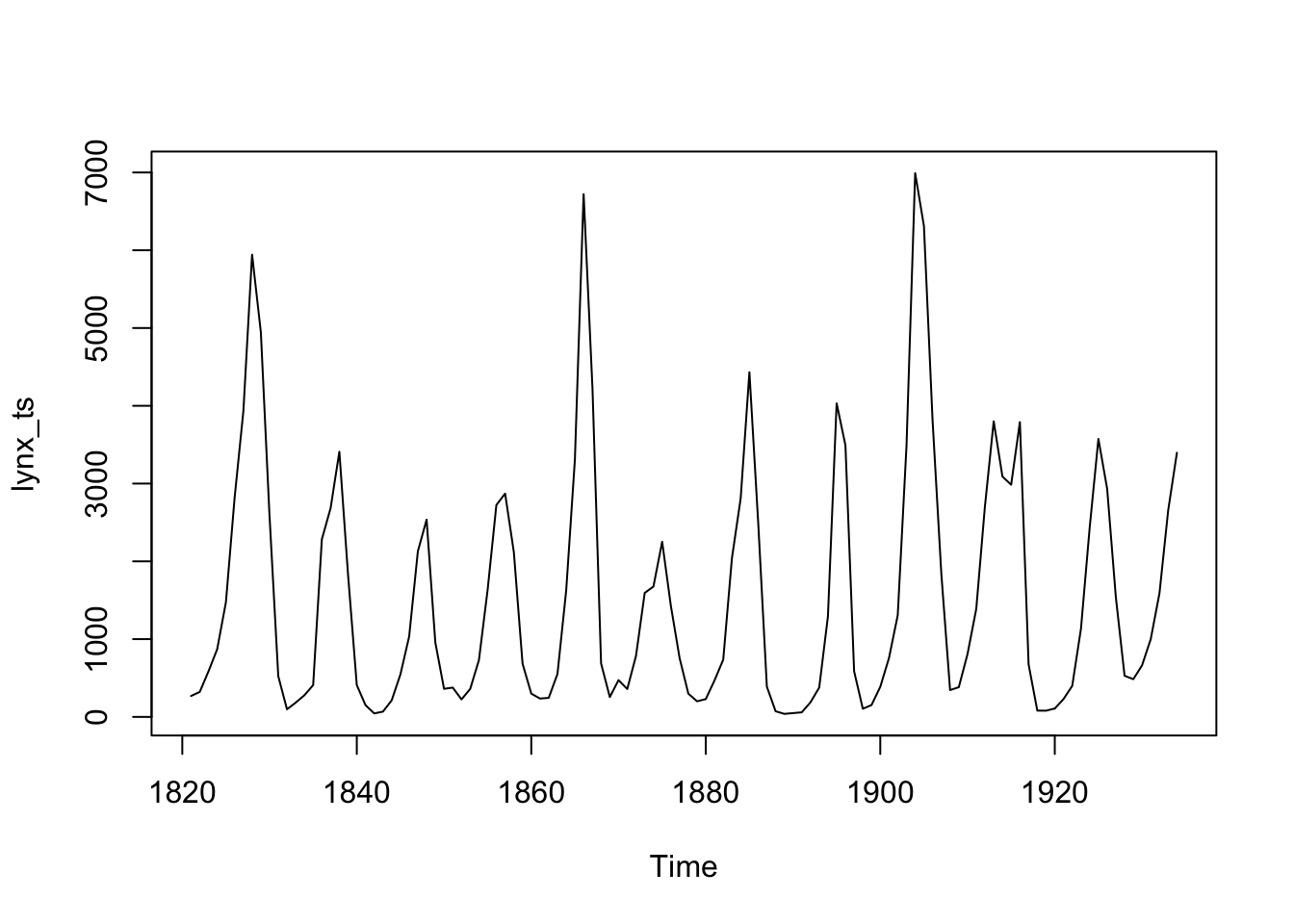
Nous voyons clairement des pics tous les 10 ans… mais aussi des pics plus importants tous les 40 ans, suggérant la présence d’un second cycle superposé au premier. Commençons par lisser notre série avec une moyenne mobile d’ordre 5 pour cibler le cycle de 10 ans.
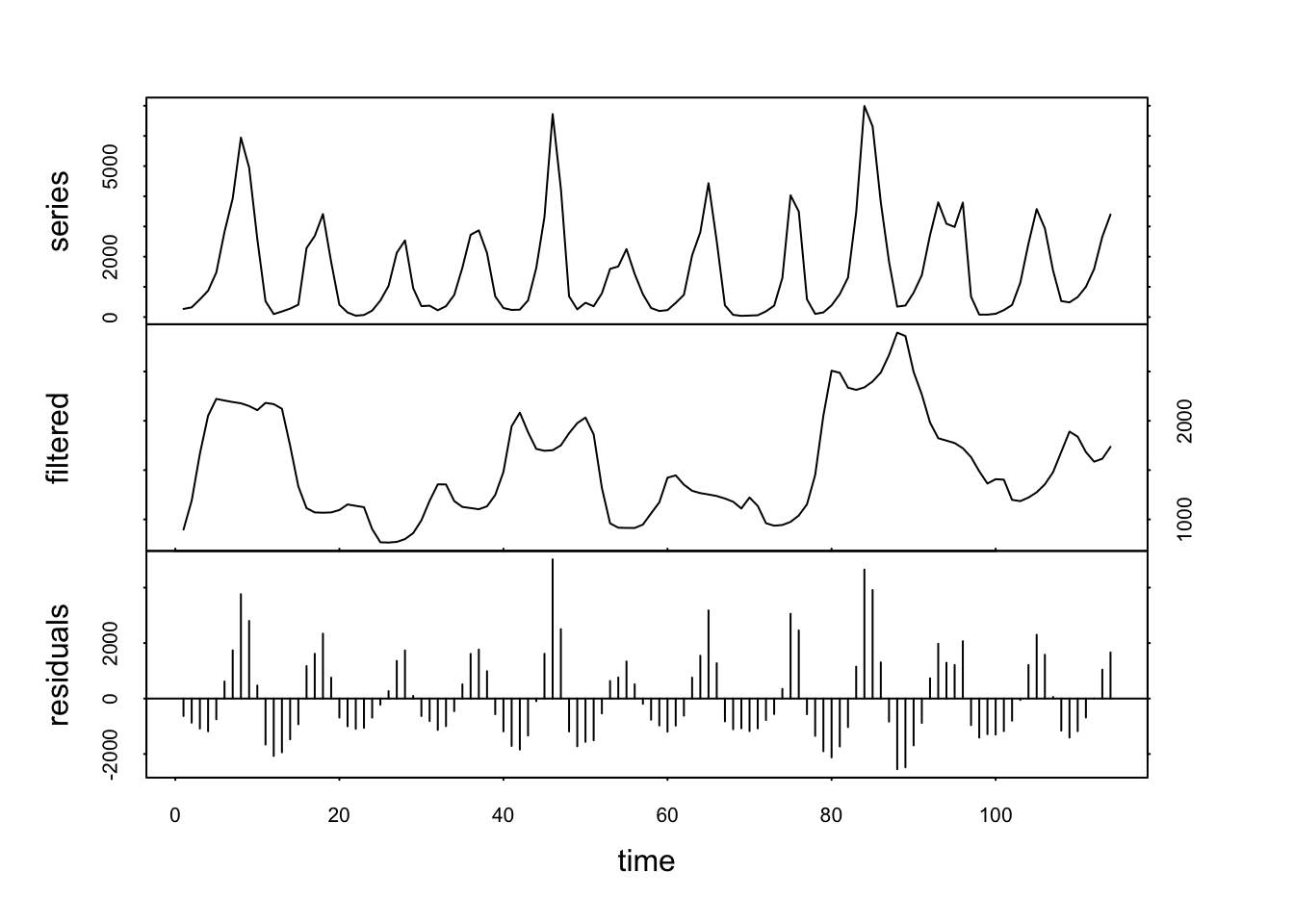
Le signal filtré est encore très chaotique, mais il se lisse très rapidement si nous répétons plusieurs fois le lissage. Voilà ce que cela donne déjà avec times = 3 :
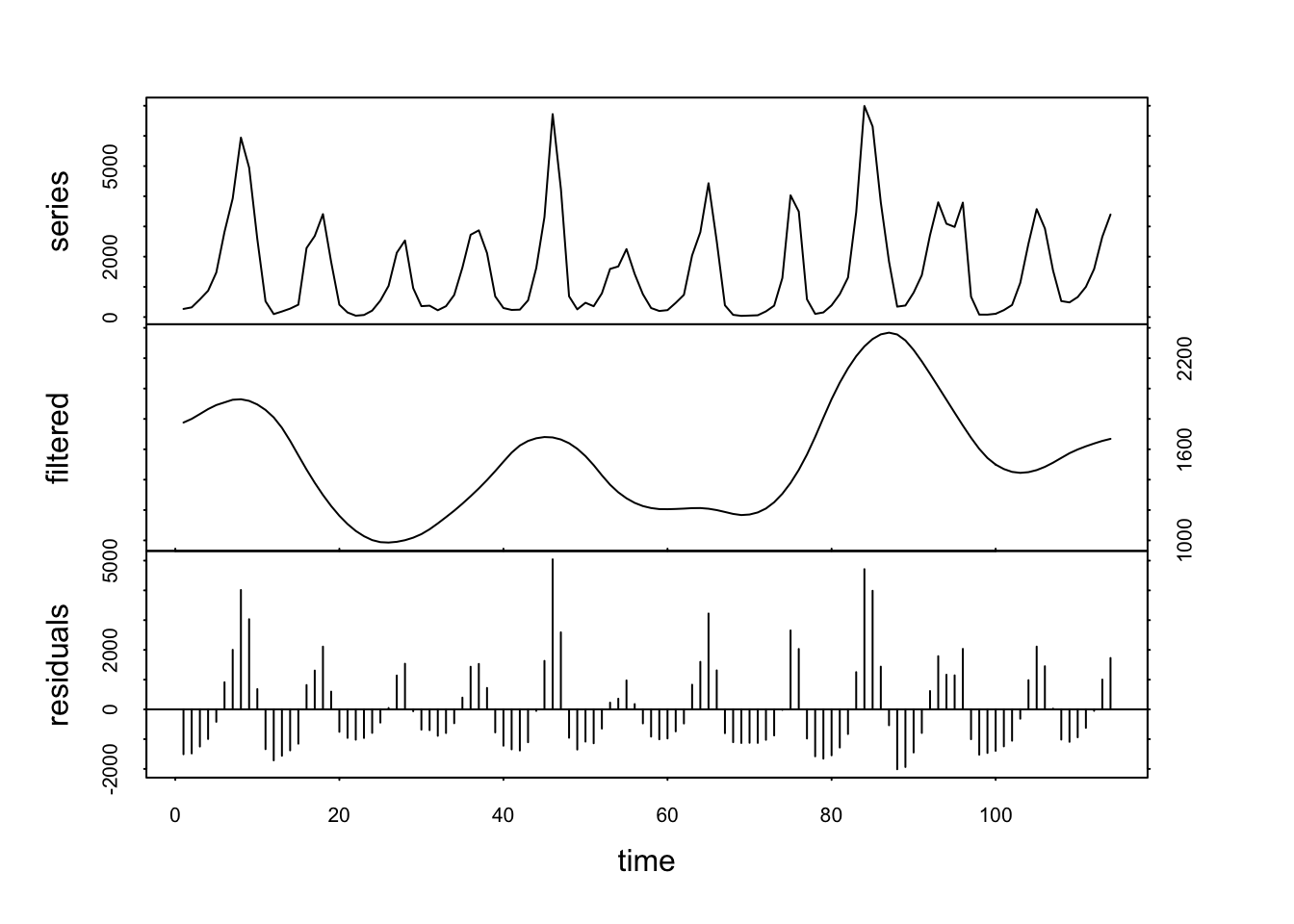
Ici, nous voyons clairement une séparation du cycle à 40 ans qui reste dans la composante filtrée, tandis que le cycle à 10 ans a été éliminé dans la composante residuals. Maintenant, si nous choisissons plutôt un ordre k = 20, nous allons cibler le cycle à 40 ans.
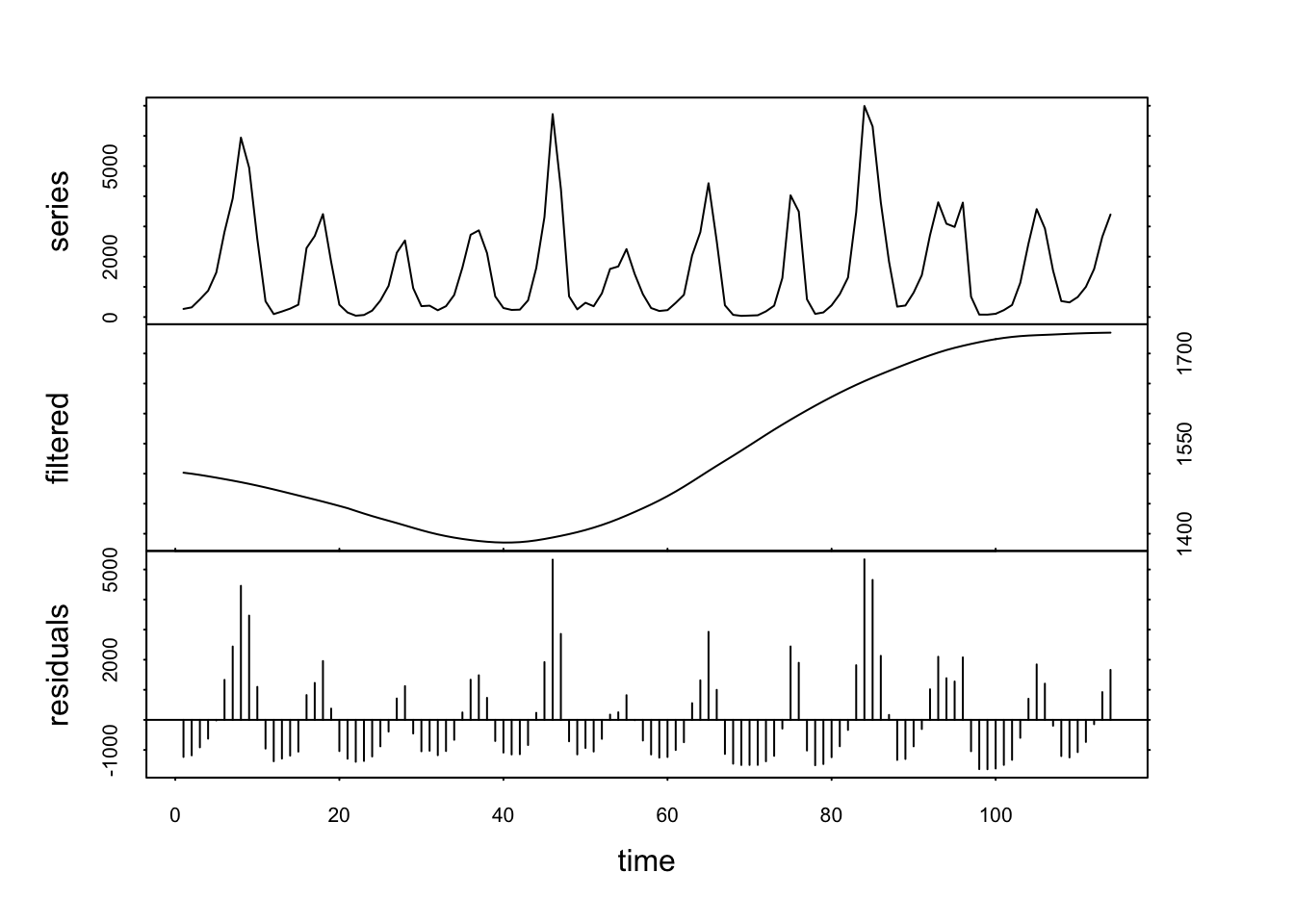
Mais ce faisant, nous avons aussi éliminé le cycle à 10 ans dans les résidus ! Rappelez-vous que la moyenne mobile filtre également des signaux de fréquences dont la bande de lissage est multiple, dont ici à 10 ans. Il nous reste alors une tendance générale qui diminue légèrement pour remonter ensuite. Donc, en travaillant avec les moyennes mobiles, nous devons cibler en premier les cycles de plus grande fréquence.
À vous de jouer !
Réalisez le travail C05Ia_tsd.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2022-12-05 11:00:00.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.
5.2.2 Médianes mobiles
Comme vous l’avez certainement deviné, les médianes mobiles fonctionnent comme les moyennes mobiles en baladant une fenêtre de largeur fixe le long de la série, mais cette fois-ci en calculant à chaque fois la médiane. Alors que la moyenne mobile s’exprime sous forme d’une somme de termes, ce qui l’associe à un modèle linéaire (on parle donc de filtrage linéaire), les médianes mobiles représentent par contre un lissage non linéaire. Il est possible de montrer que la répétition de cette opération conduit finalement à stabiliser le signal filtré. Cette courbe est caractérisée par une série de paliers successifs. Ainsi, la technique est utile pour segmenter une série, ce qui se rapproche des sommes cumulées pour détecter des transitions brusques dans la série (mais ici au lieu de les détecter, nous les mettons en évidence via le filtrage).
Exemple
Appliquons la méthode des médianes mobiles sur le signal de fluorescence dans marphy, dans l’espoir de séparer les masses d’eaux à niveaux de fluorescence différents.
fluo <- ts(read("marphy", package = "pastecs")$Fluorescence)
plot(fluo, xlab = "Transect Nice - Calvi (stations)")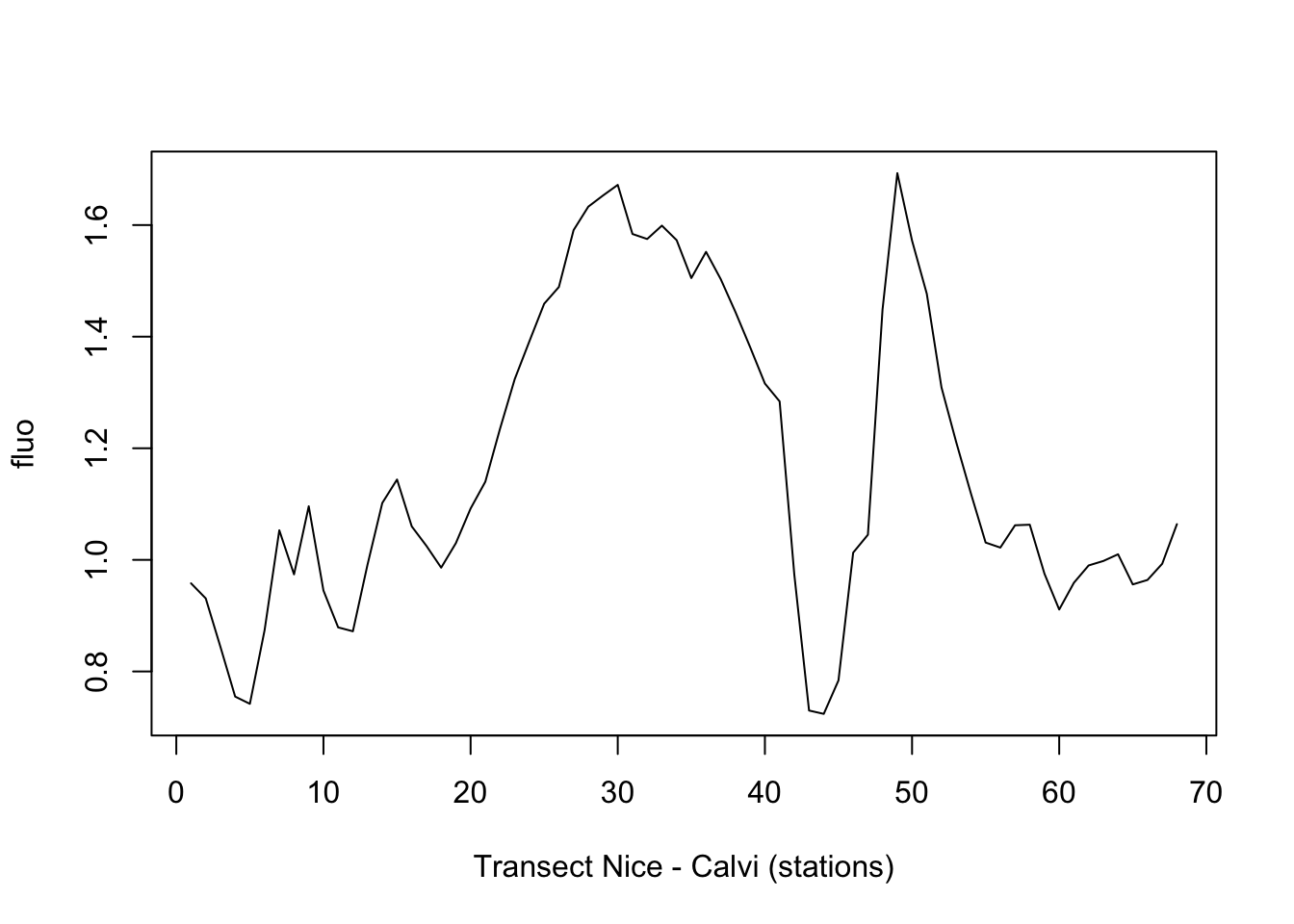
Que donne une fenêtre d’ordre 5 ? (ici, il faut essayer différentes valeurs, il n’y a pas de règle a priori).
fluo_smooth <- tsd(fluo, method = "median", order = 5, times = 1)
plot(fluo_smooth, xlab = "Transect Nice - Calvi (stations)")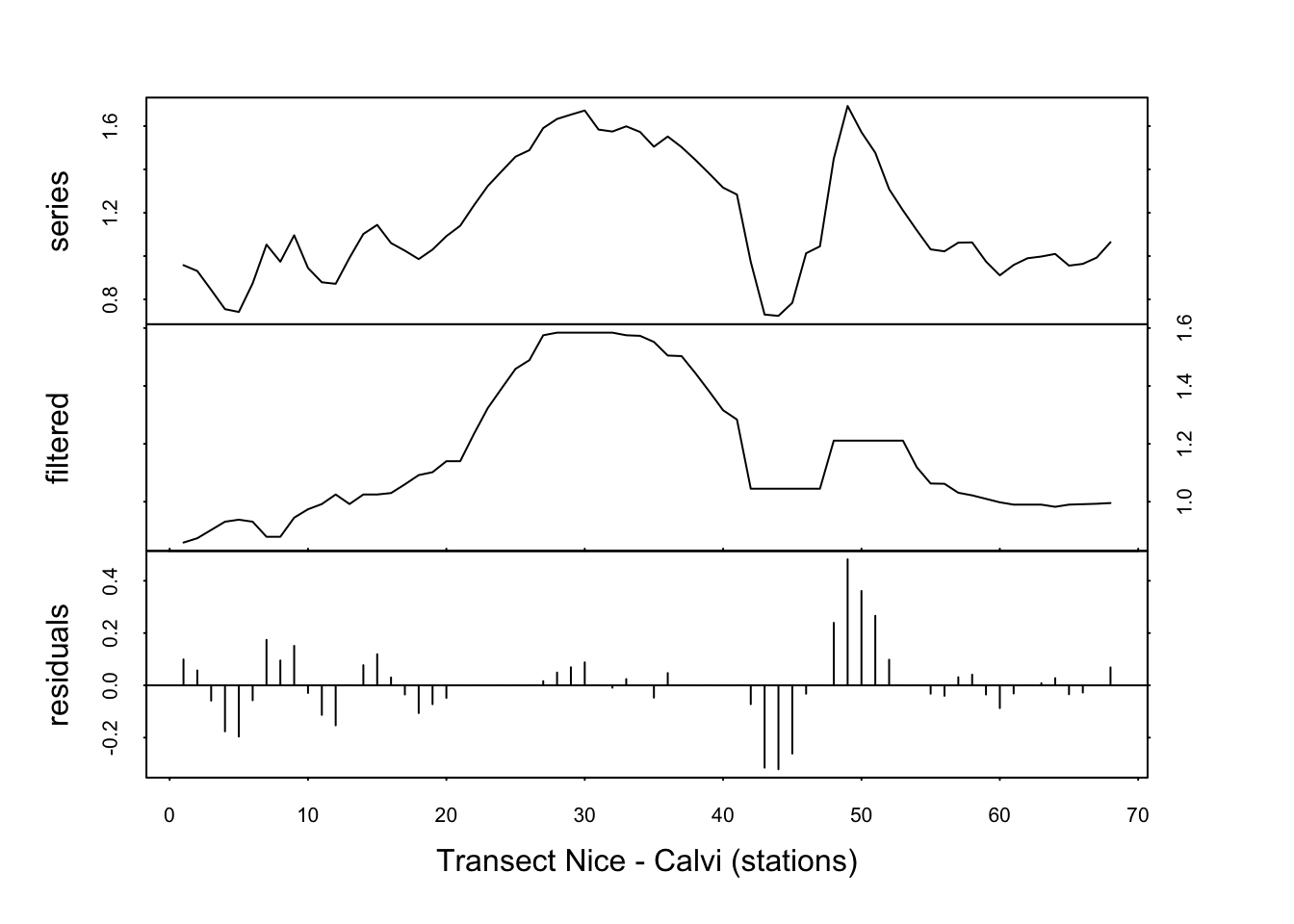
L’effet n’est pas flagrant ici. Répétons l’opération trois fois.
fluo_smooth <- tsd(fluo, method = "median", order = 5, times = 3)
plot(fluo_smooth, xlab = "Transect Nice - Calvi (stations)")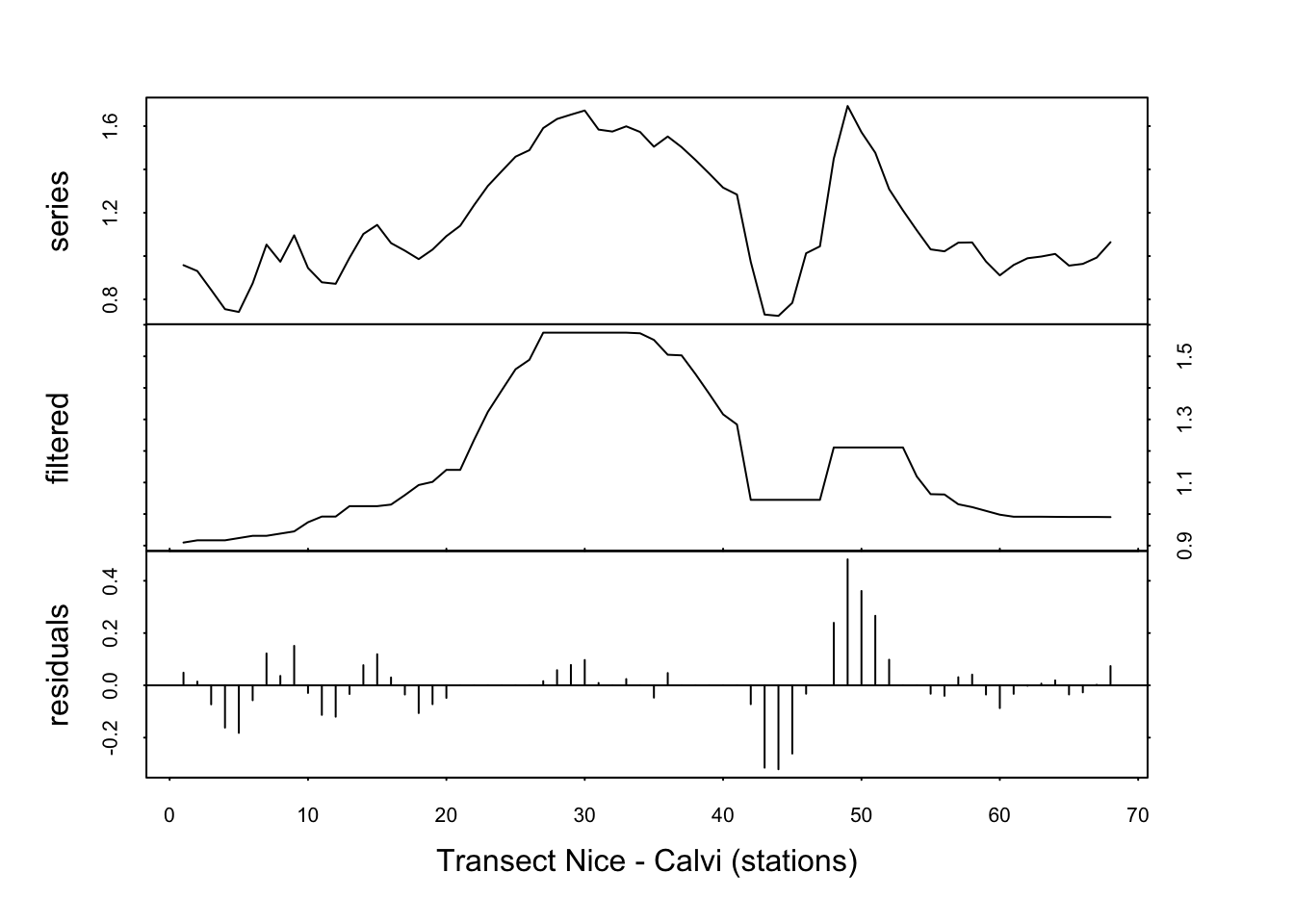
… et puis dix fois.
fluo_smooth <- tsd(fluo, method = "median", order = 5, times = 10)
plot(fluo_smooth, xlab = "Transect Nice - Calvi (stations)")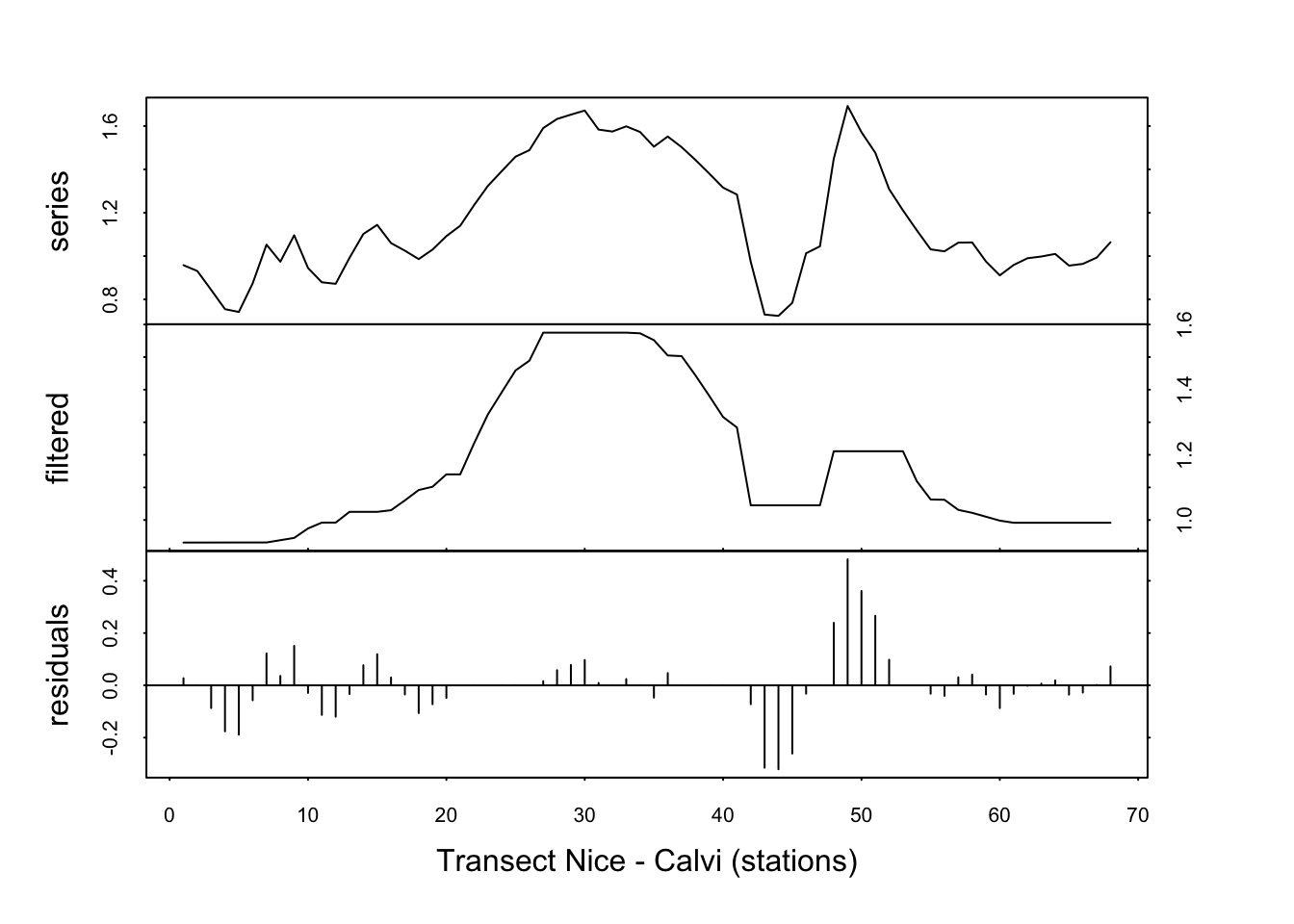
Le signal est quasiment identique entre times=3 et times=10. Nous avons effectivement stabilisé la courbe lissée par l’application répétée des médianes mobiles. Nous voyons ici clairement apparaître le pic de fluorescence caractéristique d’une production en phytoplancton importante au niveau du front (remontée d’eaux froides profondes, riches en nutriments).
Ce genre de lissage se représente mieux en superposant le signal de départ et la série lissée. Ceci est possible en indiquant stack = FALSE et resid = FALSE lors de l’appel de plot() :
plot(fluo_smooth, stack = FALSE, resid = FALSE, col = 1:2,
xlab = "Transect Nice - Calvi (stations)")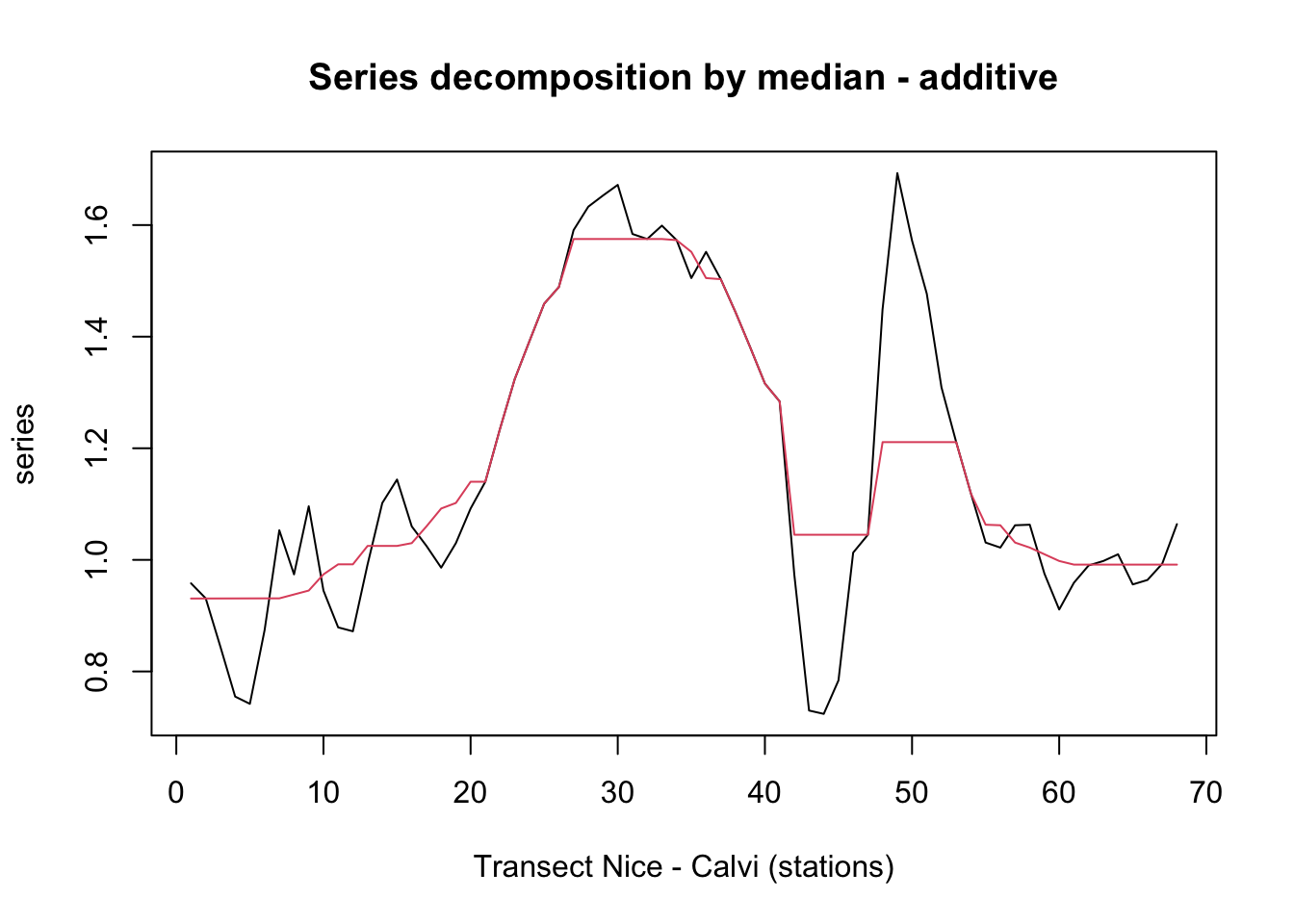
Les pics sont bien ici remplacés par des paliers.
5.2.3 Filtrage par différences
La méthode des différences a pour but d’éliminer la tendance. Ce n’est valable que si la série a une tendance monotone et non en “dents de scie”. Autrement dit, cela suppose que la série est autocorrélée positivement ou négativement.
Nous allons ici récupérer l’opérateur retard \(LX_t\) vu tout au début du module 4. Cet opérateur décale la série d’une ou plusieurs observations (argument lag=) par rapport à la série d’origine. La méthode des différences consiste à soustraire la série ainsi décalée par rapport à la série de départ. Naturellement, le filtrage peut être répété plusieurs fois pour en amplifier l’effet. Ce filtrage est également linéaire.
À condition de ne pas avoir également un cycle important, le filtrage par différences est efficace pour éliminer une tendance monotone croissante ou décroissante, voire une tendance de forme quelconque, mais dont la courbure varie lentement (signal à très haute fréquence). Dans ce cas, la méthode est très efficace pour stationnariser une série.
Exemple
Toujours pour le signal de fluorescence dans marphy, nous pouvons éliminer la tendance générale comme ceci (les valeurs optimales pour lag= et times= sont à trouver de manière empirique ici) :
fluo_stat <- tsd(fluo, method = "diff", lag = 2, times = 1)
plot(fluo_stat, xlab = "Transect Nice - Calvi (stations)")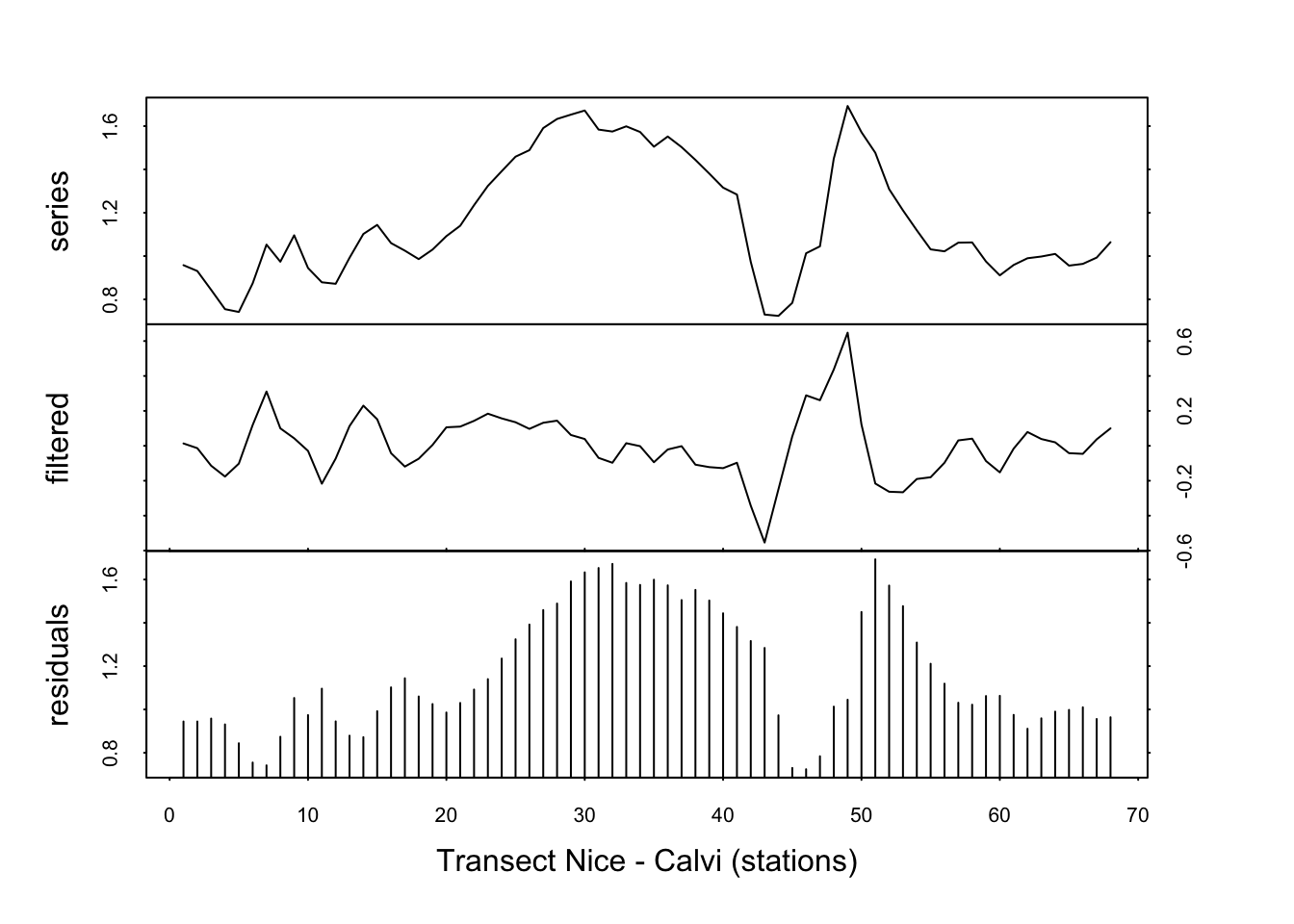
Malheureusement, en présence de cycles importants, la méthode n’est pas très efficace, même si le décalage est choisi pour coïncider avec le cycle. Ainsi pour co2, nous aurons :
co2 <- read("co2", package = "datasets")
co2_stat <- tsd(co2, method = "diff", lag = 12, times = 1)
plot(co2_stat)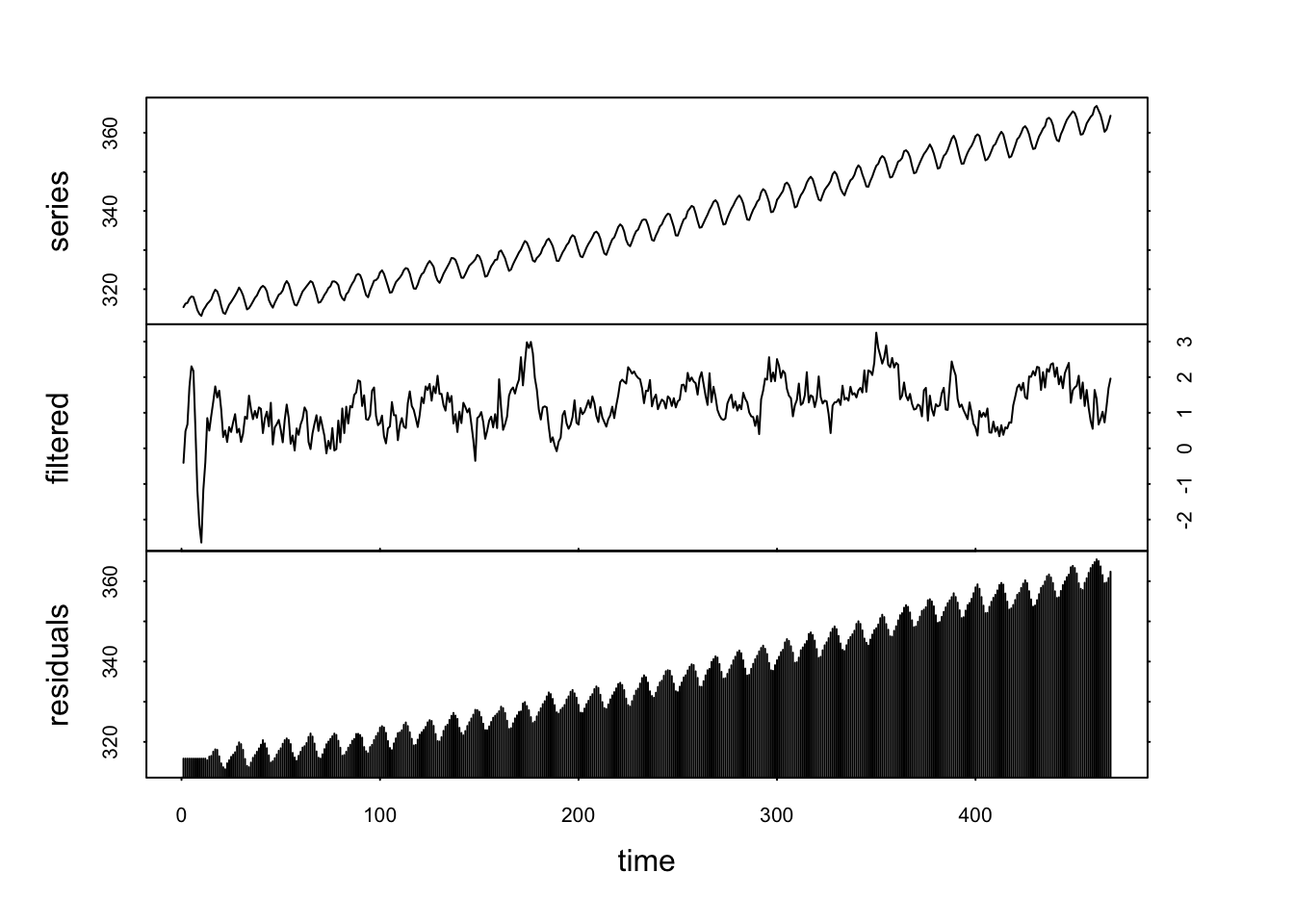
Comme nous pouvons le voir, la tendance a bien été éliminée, mais malheureusement, le cycle saisonnier est également passé à la trappe, et ce malgré notre précaution de faire coïncider le décalage (lag=) avec les fréquences du cycle. Les méthodes de décomposition de type LOESS ou l’ajustement d’un modèle sur la tendance par régression donnent souvent de meilleurs résultats pour estimer et éliminer une tendance à long terme. Cependant, le filtrage par les différences rend des services utiles lorsque la série est croissante ou décroissante avec du bruit blanc.
5.2.4 Filtrage par les valeurs propres
Le filtrage par les valeurs propres (eigenvector filtering en anglais, ou EVF en abrégé) consiste à décomposer le signal original de la série via une analyse en composantes principales. Nous parlons aussi d’Analyse en Composantes Principales de Processus ou ACPP. Le principe du calcul consiste à créer une matrice contenant la série initiale en dernière colonne et des colonnes supplémentaires avec des décalages successifs de cette série initiale d’un pas de temps toujours identique \(\tau\) m fois pour former m + 1 colonnes au total. Naturellement, pour obtenir une matrice carrée, nous éliminons les premières et les dernières valeurs des différentes colonnes de la matrice jusqu’à réduire à un tableau rectangulaire sans valeurs manquantes. Cela nous donne une matrice X comme ceci :
\[X = \begin{pmatrix} X_{1 + m \tau} & \cdots & X_{1 + 2 \tau} & X_{1 + \tau} & X_1 \\ X_{2 + m \tau} & & X_{2 + 2 \tau} & X_{2 + \tau} & X_2 \\ X_{3 + m \tau} & & X_{3 + 2 \tau} & X_{3 + \tau} & X_3 \\ \vdots & \ddots & & & \vdots \\ X_n & \cdots & X_{n - (m - 2) \tau} & X_{n - (m - 1) \tau} & X_{n - m \tau} \end{pmatrix} \]
Notez que cette matrice fait penser au calcul réalisé pour déduire la fonction d’autocorrélation, comprenez qu’elle contient des informations relatives à l’autocorrélation de la série à des pas de temps croissants le long de ses lignes. Ensuite, nous traitons cette matrice comme si c’était un jeu de données multivarié via une ACP classique sans réduction (calcul sur base de la variance-covariance).
La première composante principale capture le signal de plus forte variance et les composantes principales suivantes la compléteront avec des signaux de variance décroissante. Notez que ces signaux peuvent être de formes diverses : aussi bien des tendances plus ou moins monotones que des cycles ou d’autres structures. Le signal qui ressortira en première composante sera une tendance générale si la série est dominée par un tel signal. Elle sera un cycle si celui-ci est prépondérant.
Enfin, nous pouvons filtrer la série en choisissant de ne conserver que les i premières composantes avec i < (m + 1), voire même, en sélectionnant des composantes principales spécifiques (par exemple, la première et la troisième en indiquant axes = c(1, 3)). Plus le nombre de composantes conservées est faible, plus le filtrage sera important. Si nous conservons toutes les composantes, nous recréons la série à l’identique. Pour plus de facilité, \(/tau\) est systématiquement choisi équivalent au pas de temps de la série régulière. Par contre, nous devons indiquer le décalage maximum \(m \times \tau\) souhaité (argument lag =). Si ce décalage est très faible, nous ne filtrerons pas beaucoup la série, car nous serons obligés de prendre quasiment toutes les composantes principales calculées. Si le décalage est trop grand, nous tronquerons trop au début et à la fin notre série et ses variantes décalées successivement pour faire rentrer le tout dans une matrice carrée. De plus, nous risquons de filtrer beaucoup trop fort notre série jusqu’à la réduire, à la limite à pratiquement une droite de tendance générale. Le choix de ce décalage maximum peut être guidé efficacement via l’observation de la fonction d’autocorrélation, et notamment en regardant après combien de décalages cette ACF passe par zéro (ce que l’on appelle l’échelle caractéristique du processus). Nous prendrons un décalage maximum d’environ quatre fois cette valeur comme point de départ de nos essais, si la longueur de la série le permet.
Exemple
Le cas du signal EEG est compliqué, car le signal (a priori de forme quelconque) est très bruité. Testons un filtrage par les vecteurs propres en ne conservant que la première composante principale.
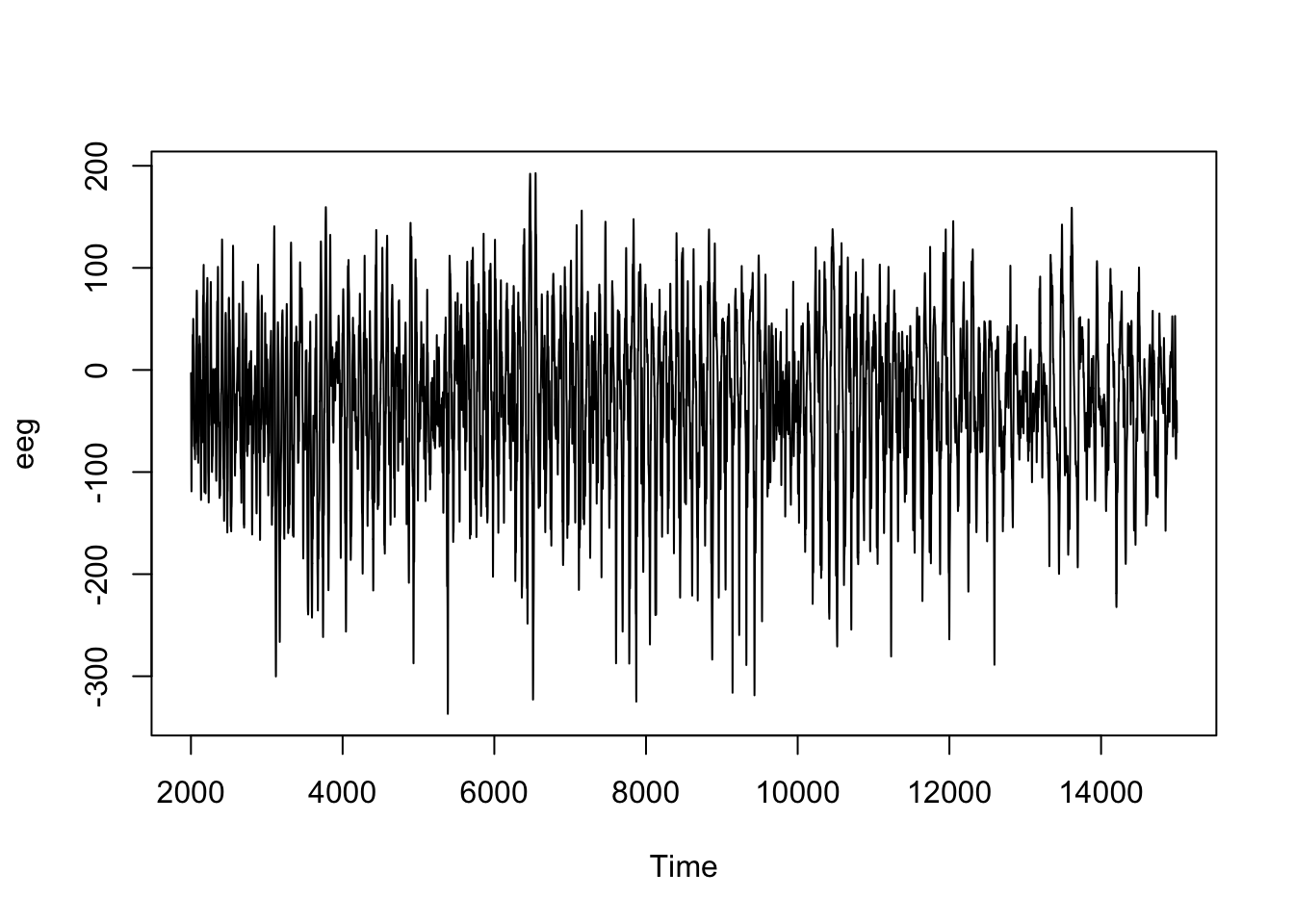
L’échelle caractéristique du processus s’obtient via le graphique de l’autocorrélation :
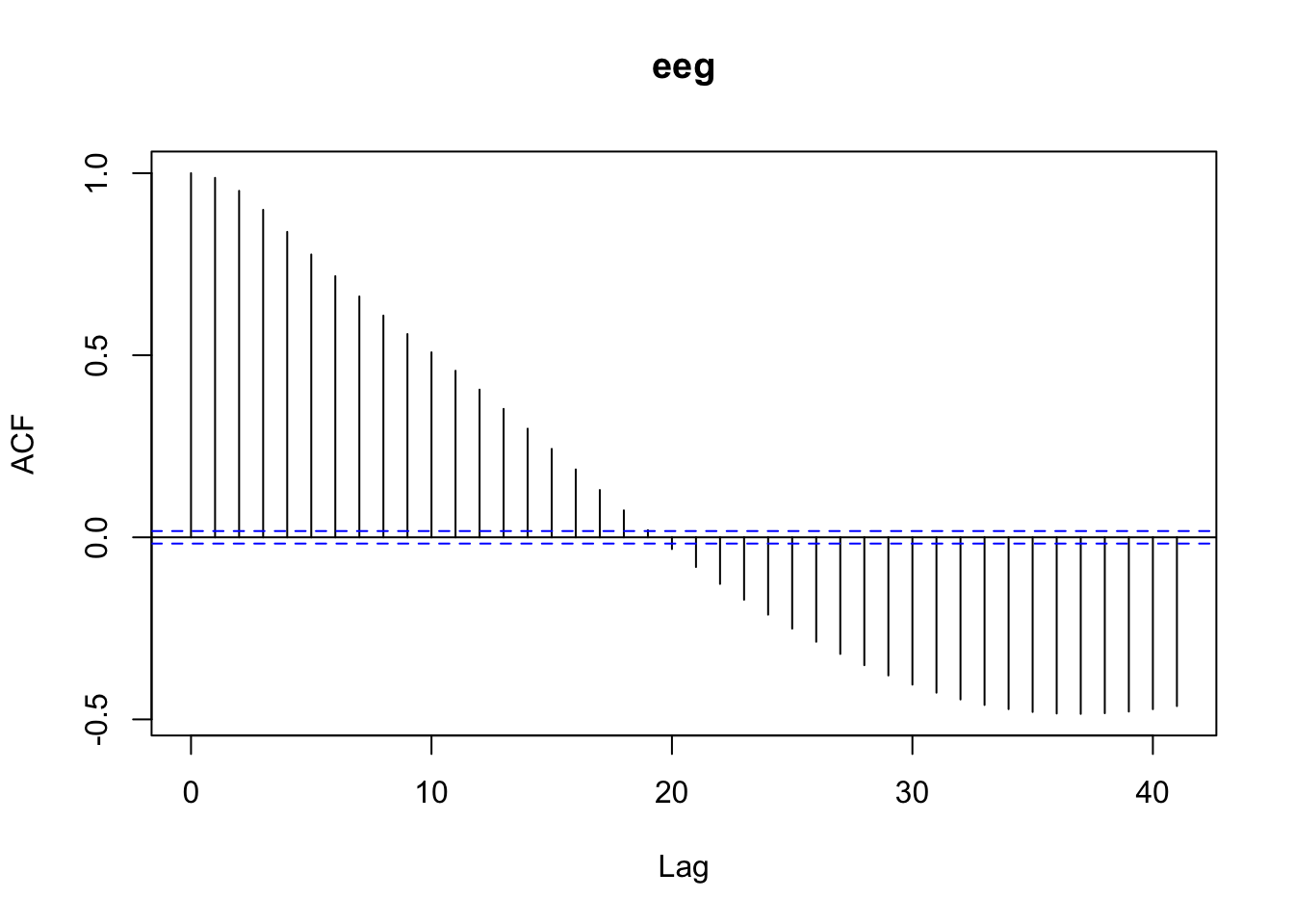
Nous voyons qu’il s’agit ici d’un décalage de 20 fois le pas de temps. Nous choisissons donc lag = 80 pour notre filtrage par les vecteurs propres et ne conservons que le premier axe de l’ACP.
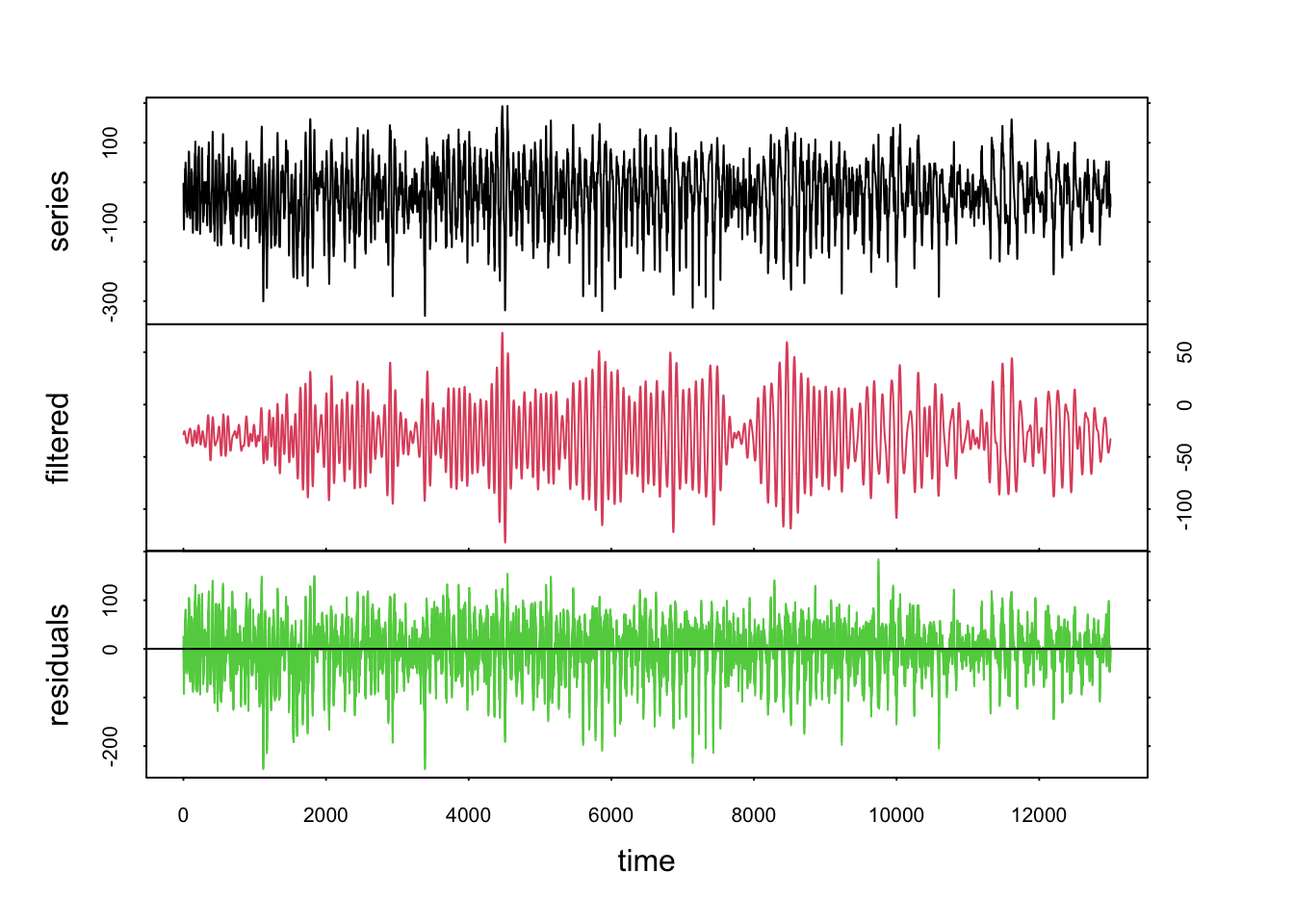
La série originale bruitée en noir est transformée en un signal beaucoup plus propre dans la courbe en rouge. Les résidus sont dans la série en vert.