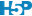2.4 Quantification vectorielle
Un des désavantages de la méthode des k plus proches voisins est que l’on doit conserver toutes les données du set d’apprentissage et confronter systématiquement tout nouvel individu à l’ensemble des cas de ce set. L’idée sous-jacente à la quantification vectorielle (learning vector quantization en anglais, LVQ en abrégé) est que les données initiales peuvent sans doute être synthétisées : des individus proches dans l’espace de Malahanobis peuvent être remplacés par des “individus moyens ou centroïdes” tout en apportant à peu près le même effet. Du coup, nous réduisons la quantité d’information à conserver et nous accélérons les calculs dans les phases de test et déploiement.
Une étape supplémentaire dans le calcul du classifieur est introduite. Le set d’apprentissage initial est résumé en un dictionnaire ou codebook en anglais, dans lequel les groupes initiaux sont remplacés par un ou plusieurs centroïdes. Ces centroïdes sont, en quelque sorte, des “portraits robots” des différentes classes et ils résument les caractéristiques des individus appartenant à ces classes. La classification supervisée se fait par une méthode similaire aux k plus proches voisins, mais en utilisant les centroïdes du dictionnaire en lieu et place des individus du set d’apprentissage.
En plus du paramètre k, il faut donc également définir size=, le nombre de centroïdes qui seront calculés dans le dictionnaire. Il est possible de calculer librement les différents centroïdes en fonction de la dispersion des données, ou bien d’imposer que le même nombre de centroïdes soit calculé pour chaque classe.
2.4.1 Pima avec LVQ
Voyons ce que cela donne sur nos données pima1 et pima2, en utilisant la fonction mlLvq() de {mlearning} qui utilise les arguments size= pour la taille du dictionnaire et k.nn= pour le nombre de proches voisins à considérer ensuite :
set.seed(846)
pima1_lvq <- mlLvq(data = pima1, diabetes ~ ., k.nn = 3, size = 30)
pima1_lvq_conf <- confusion(cvpredict(pima1_lvq, cv.k = 10), pima1$diabetes)
plot(pima1_lvq_conf)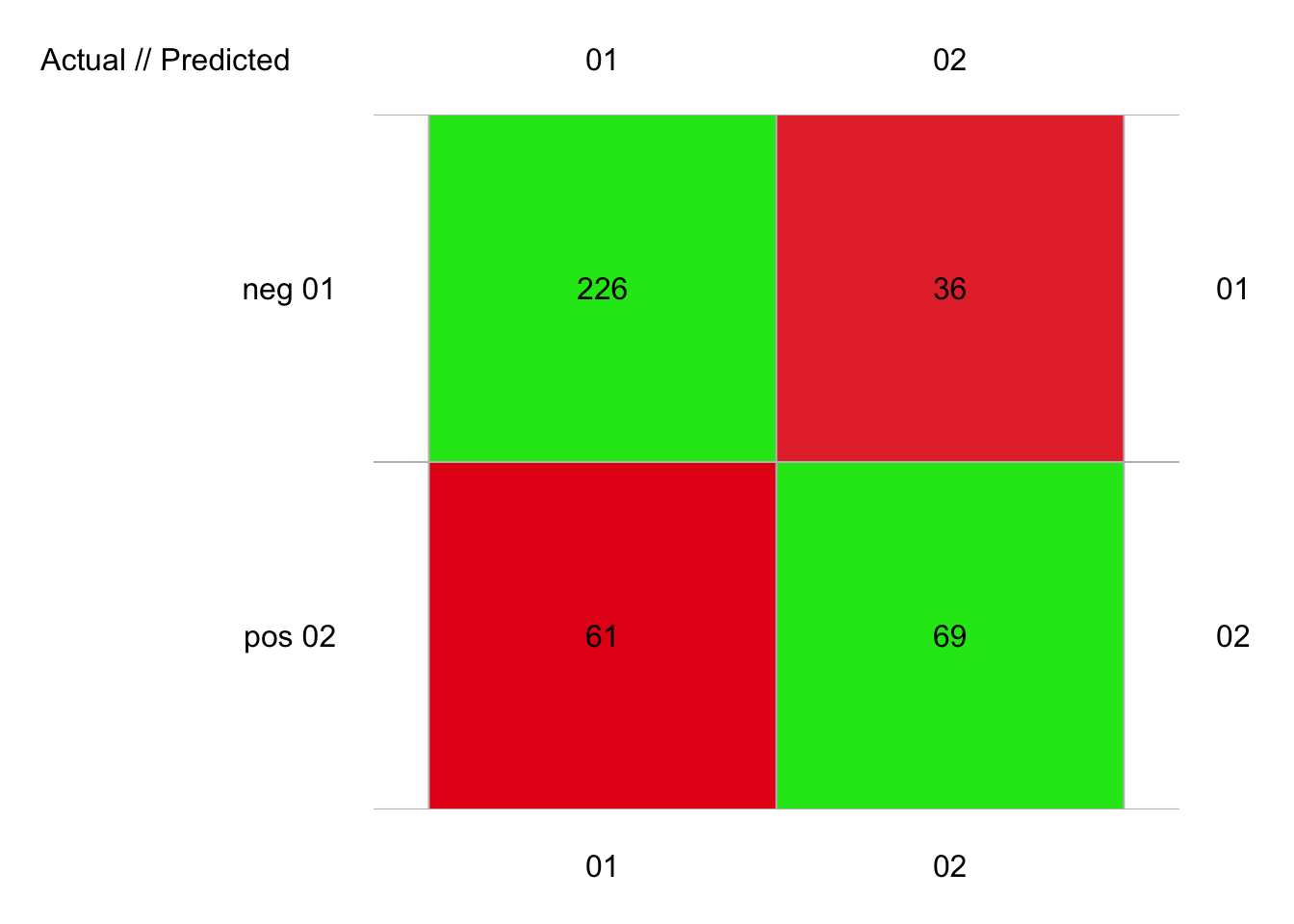
# 392 items classified with 295 true positives (error = 24.7%)
#
# Global statistics on reweighted data:
# Error rate: 24.7%, F(micro-average): 0.709, F(macro-average): 0.705
#
# # A data.frame: 2 x 3
# ` ` Fscore Recall Precision
# <rownames> <dbl> <dbl> <dbl>
# 1 neg 0.823 0.863 0.787
# 2 pos 0.587 0.531 0.657Nous avons choisi arbitrairement de prendre un dictionnaire de taille 30 et 3 plus proches voisins. Avec ces valeurs, nous avons 25% d’erreur, ce qui nous situe entre k-NN et ADL en termes de performances. Essayez par vous-même d’autres valeurs de size = et k.nn = pour optimiser encore ce résultat.
Avec pima2, une taille de dictionnaire de 30 toujours et trois plus proches voisins, nous obtenons 24% d’erreur :
set.seed(25)
pima2_lvq <- mlLvq(data = pima2, diabetes ~ ., k.nn = 3, size = 30)
pima2_lvq_conf <- confusion(cvpredict(pima2_lvq, cv.k = 10), pima2$diabetes)
plot(pima2_lvq_conf)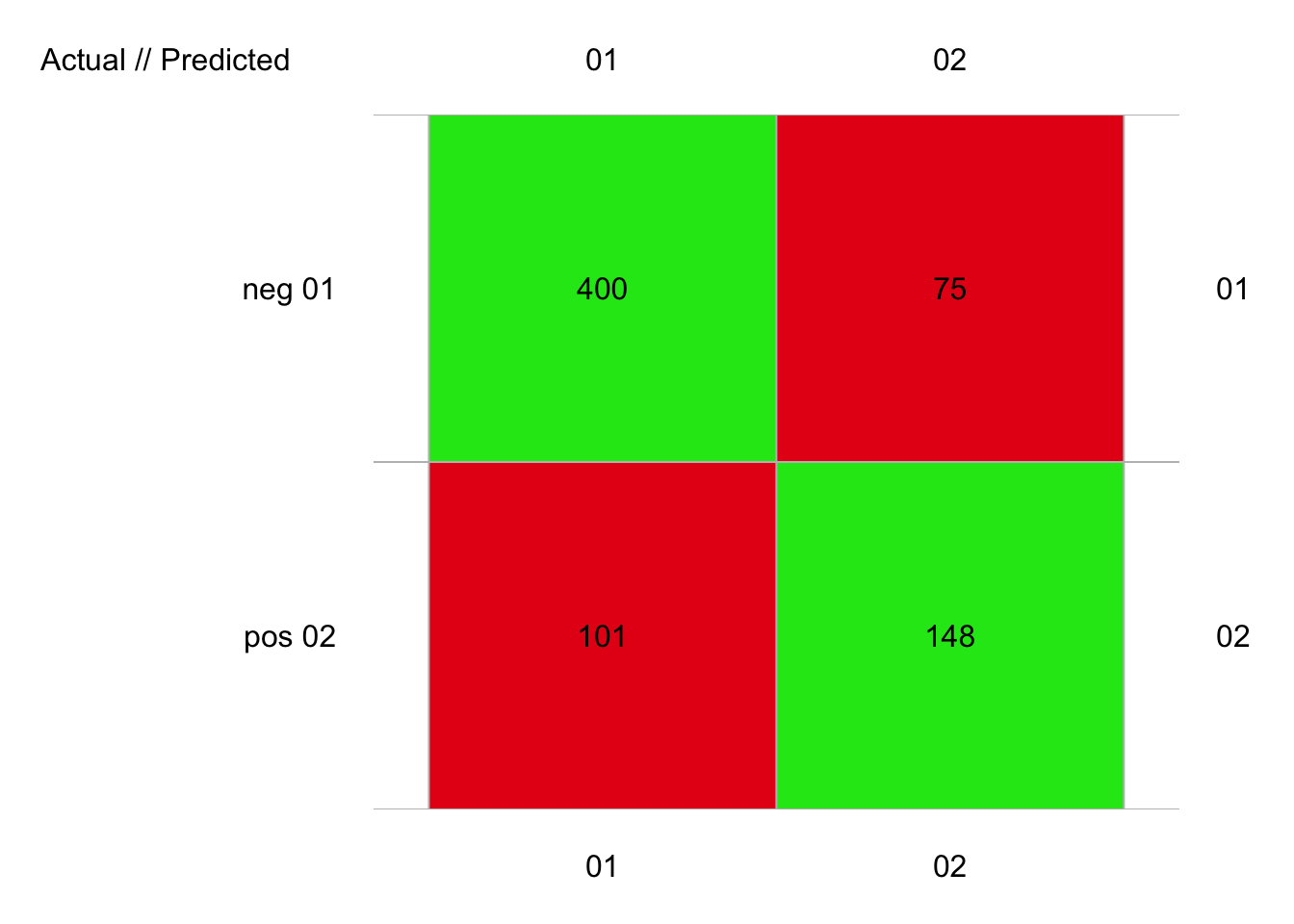
# 724 items classified with 548 true positives (error = 24.3%)
#
# Global statistics on reweighted data:
# Error rate: 24.3%, F(micro-average): 0.725, F(macro-average): 0.723
#
# # A data.frame: 2 x 3
# ` ` Fscore Recall Precision
# <rownames> <dbl> <dbl> <dbl>
# 1 neg 0.820 0.842 0.798
# 2 pos 0.627 0.594 0.664À vous de jouer !
Réalisez le travail C02Ia_zooplankton.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2022-10-28 12:30:00.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.