5.5 Régularisation
La régularisation d’une série spatio-temporelle permet de transformer une série échantillonnée avec un pas de temps irrégulier ou présentant des trous en une série régulière. Malheureusement, en biologie, on a rarement affaire à des séries parfaitement régulières, soit parce qu’il y a des observations manquantes, soit parce qu’on ne contrôle pas l’intervalle de temps. Dans ce cas, la régularisation est une opération préliminaire indispensable à beaucoup d’analyses de séries spatio-temporelles, que ce soit avec les outils {pastecs} ou avec d’autres méthodes. Les objets ts doivent être d’office des séries spatio-temporelles régulières dans R. Cette étape est donc requise pour adapter des data frames avant de pouvoir les transformer en séries temporelles ! Plusieurs méthodes de régularisation sont disponibles dans {pastecs} : régularisation par valeur constante (regconst()), linéaire (reglin()), par courbes splines (regspline()) et par la méthode des aires (regarea()). Afin de simplifier le travail de régularisation, et de faciliter ensuite la création des séries temporelles, toutes ces fonctions ont été regroupées sous une fonction commune regul(), dans la même philosophie que tsd() regroupe les différentes techniques de décomposition, par ailleurs implémentées par les fonctions decXXX().
Quelle que soit la méthode utilisée, on doit veiller à obtenir un pas de temps de la série régulière aussi proche que possible du pas de temps (moyen) de la série échantillonnée. De même, on doit aussi essayer d’obtenir autant de valeurs non interpolées que possible dans la série régulière finale. Quant à l’extrapolation (obtenue à l’aide de l’argument rule = 2), elle est à proscrire. La fonction regul() admet beaucoup de paramètres. Vous êtes invité à essayer différents réglages sur vos propres données, et à visualiser le résultat à l’aide de plot.regul() et hist.regul() pour vous familiariser avec ses possibilités. La transformation du temps depuis un décompte des jours vers une “année numérique simplifiée” (longueur de 365,25 jours, et chaque mois correspondant à exactement 1/12 de cette valeur) n’est pas très intuitive, mais une fois que l’on a compris le principe, c’est très facile à faire avec l’argument units = "daystoyears" de regul() (voir l’exemple ci-dessous).
Dans le cas où l’on voudrait condenser des données (par exemple, transformer un échantillonnage mensuel en valeurs saisonnières ou des données quotidiennes en série par semaine ou par mois), il vaut mieux agréger les données en calculant des moyennes ou des médianes successives. On peut aussi régulariser la série avec le pas temps initial si ce dernier est un multiple du pas de temps visé, et utiliser ensuite la fonction aggregate() de R, que nous avons déjà utilisée.
Dans le cadre de ce cours, la régularisation de série irrégulière est une matière optionnelle. La présentation très succincte ci-dessus vous permet de prendre connaissance de l’existence de ces techniques (faites toujours ?<nom_de_function pour lire la page d’aide de chaque fonction citée comme point de départ). Revenez vers cette section, et vers les liens qu’elle renferme, si vous vous trouvez confronté à une situation où une régularisation de série est nécessaire. Le manuel de {pastecs} renferme tout un chapitre qui décrit en détail comment procéder.
5.5.1 Application pratique
Nous reprenons ici l’exemple de la régularisation d’une série phytoplanctonique très irrégulière de {pastecs} par interpolation linéaire :
Régularisation de la série Navi du jeu de données releve
Il s’agit du dénombrement de phytoplancton, et en particulier, la diatomée Navicula sp en une station unique entre le 21 mars 1989 et le 3 novembre 1992.
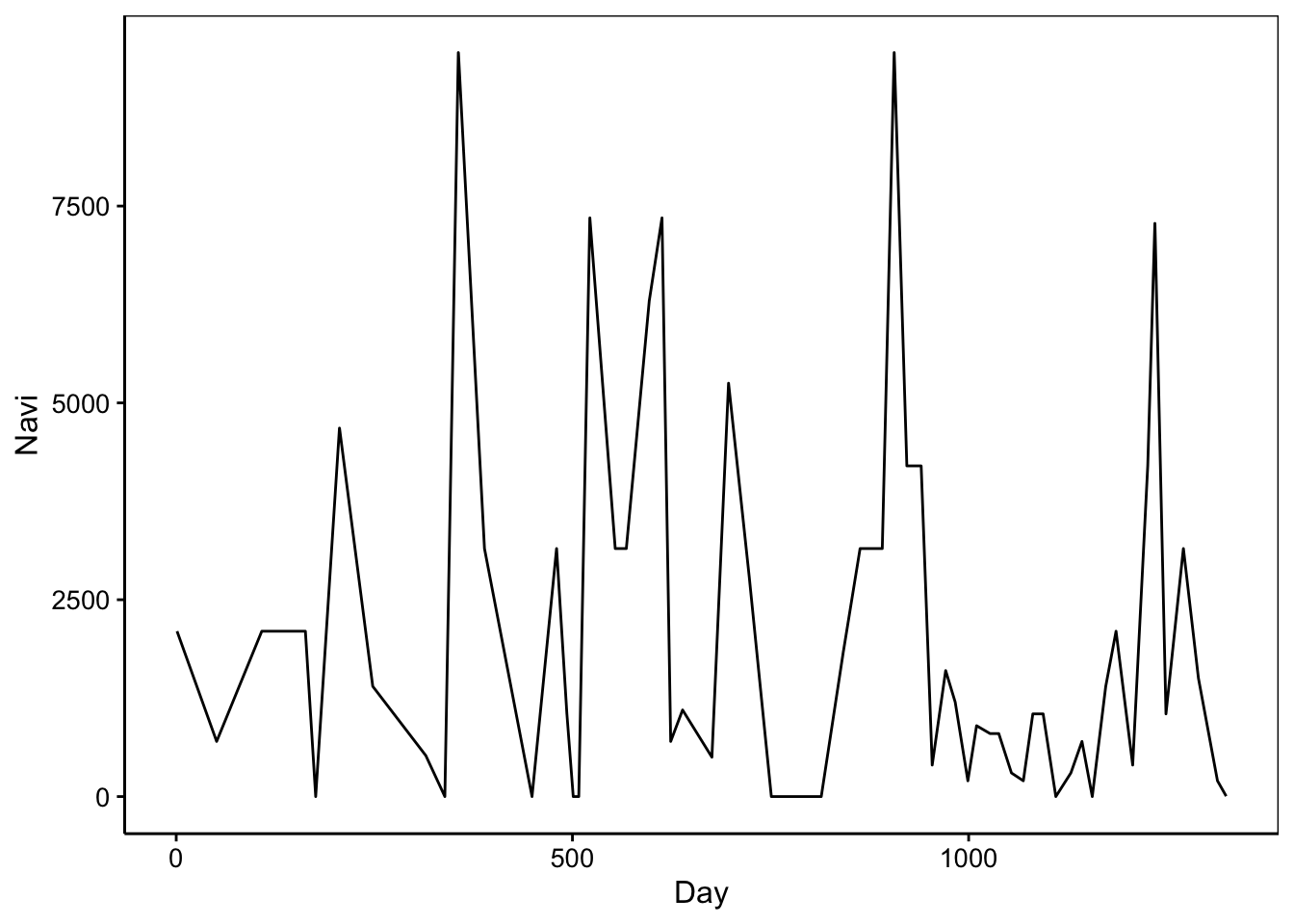
Examinons un peu le pas de temps entre les différentes observations.
# [1] 1 51 108 163 176 206 248 315 339 356 389 449 480 493 501
# [16] 508 522 554 568 597 613 624 639 676 697 723 751 786 814 842
# [31] 863 877 891 906 922 940 954 971 983 999 1010 1027 1038 1054 1069
# [46] 1081 1094 1110 1129 1143 1156 1173 1186 1207 1226 1235 1249 1271 1290 1314
# [61] 1325# [1] 61# [1] 50 57 55 13 30 42 67 24 17 33 60 31 13 8 7 14 32 14 29 16 11 15 37 21 26
# [26] 28 35 28 28 21 14 14 15 16 18 14 17 12 16 11 17 11 16 15 12 13 16 19 14 13
# [51] 17 13 21 19 9 14 22 19 24 11# [1] 7 67# [1] 22.06667Nous avons donc entre 7 et 67 jours entre deux observations avec un écart moyen de 22 jours. Ici, nous pouvons utiliser les fonctions regul.screen() et regul.adj() pour trouver le meilleur pas de temps pour la régularisation. Ce travail est réalisé dans le manuel de {pastecs} qui suggère que trois semaines (21 jours) est un bon pas de temps. Mais afin d’avoir un nombre d’observations entier (fréquence entière), nous raccourcirons quelque peu cet intervalle. Si nous considérons 18 observations par an (frequence = 18), l’intervalle de temps entre deux observations sera alors de 365.25/18 = 20,3 jours.
Nous allons donc régulariser le jeu de données avec cette valeur en convertissant le temps en unité d’année. Afin d’éviter les difficultés du calendrier (année bissextile ou non, mois de 31, 30, 29 ou 28 jours), nous allons “lisser” le temps en utilisant l’argument units = "daystoyears". En partant d’une mesure du temps écoulé depuis une date de départ en jours (dans Day), nous considérerons donc 265,25 jours par an et 1/12 d’année exactement pour chaque mois. Le début et la fin des années et des mois ne correspondront plus exactement aux débuts et fins de dates calendriers (à un jour ou deux près maximum), mais dans le cadre d’effets annuels et interannuels, cela a peu d’importance : les êtres vivants se soucient relativement peu, en général, de notre calendrier grégorien ! Par contre, ce type de manipulation ne tiendrait plus la route, par exemple, pour des données boursières ou économiques. En effet, dans ce cas, les jours de weekend et les jours fériés sont susceptibles de différer significativement du point de vue des valeurs mesurées (valeurs boursières, activité économique, déplacements liés au travail ou aux vacances, etc.).
decloess() par exemple) imposent d’exprimer le temps en unité "years". De même, il est fortement conseillé d’adopté l’unité "days" pour l’étude de cycles circadiens.
Un autre argument est aussi important ici, il s’agit de tol =. C’est la fenêtre de tolérance à gauche ou et à droite de la date requise dans la série régulière pour aller chercher une observation sans l’interpoler. Avec un pas de temps de 20 jours, on peut considérer que si nous avons à disposition une mesure la veille ou le lendemain, cela ne fera pas une grande différence. Peut-être même aussi l’avant-veille ou le surlendemain. Donc, nous prendrons une tolérance de 2 jours. Mais pour être certain de prendre les observations 2 jours avant ou après, on rajoute 10% à la valeur, donc, un tol = 2.2 jour. Nous avons à présent (presque) tout ce qu’il faut pour régulariser notre série.
navi_reg <- regul(releve$Day, releve$Navi, n = length(releve$Day),
units = "daystoyears", frequency = 18, tol = 2.2, methods = "linear",
datemin = "21/03/1989", dateformat = "d/m/Y")# A 'tol' of 2.2 in 'days' is 0.00602327173169062 in 'years'
# 'tol' was adjusted to 0.0061728395061727Le programme nous avertit que, puisque nous avons transformé l’échelle temporelle de "days" en "years", la valeur de tol = 2.2 qui était exprimée en jours devient 0.0602 en années, et est de plus ajustée à une valeur de 0.006179 afin que ce soit une fraction entière de 1/frequency (c’est-à-dire de deltat, voir ?regul). Comme releve$Day contient un décompte des jours depuis une date précise, nous devons indiquer cette date dans datemin =, et son format dans dateformat =. Nous obtenons alors ceci :
# Regulation of, by "method" :
# Series
# "linear"
#
# Arguments for "methods" :
# tol.type tol rule f
# "both" "2.2" "1" "0"
# periodic window split
# "FALSE" "22.0666666666667" "100"
#
# 49 interpolated values on 61 ( 0 NAs padded at ends )
#
# Time scale :
# start deltat frequency
# 2.043000e+03 5.555556e-02 1.800000e+01
# Time units : years
#
# call : regul(x = releve$Day, y = releve$Navi, n = length(releve$Day), units = "daystoyears", frequency = 18, datemin = "21/03/1989", dateformat = "d/m/Y", tol = 2.2, methods = "linear")Il y a beaucoup d’information dans tout ceci. Nous vous renvoyons au manuel de {pastecs} pour les explications. Passons tout de suite à la représentation graphique :
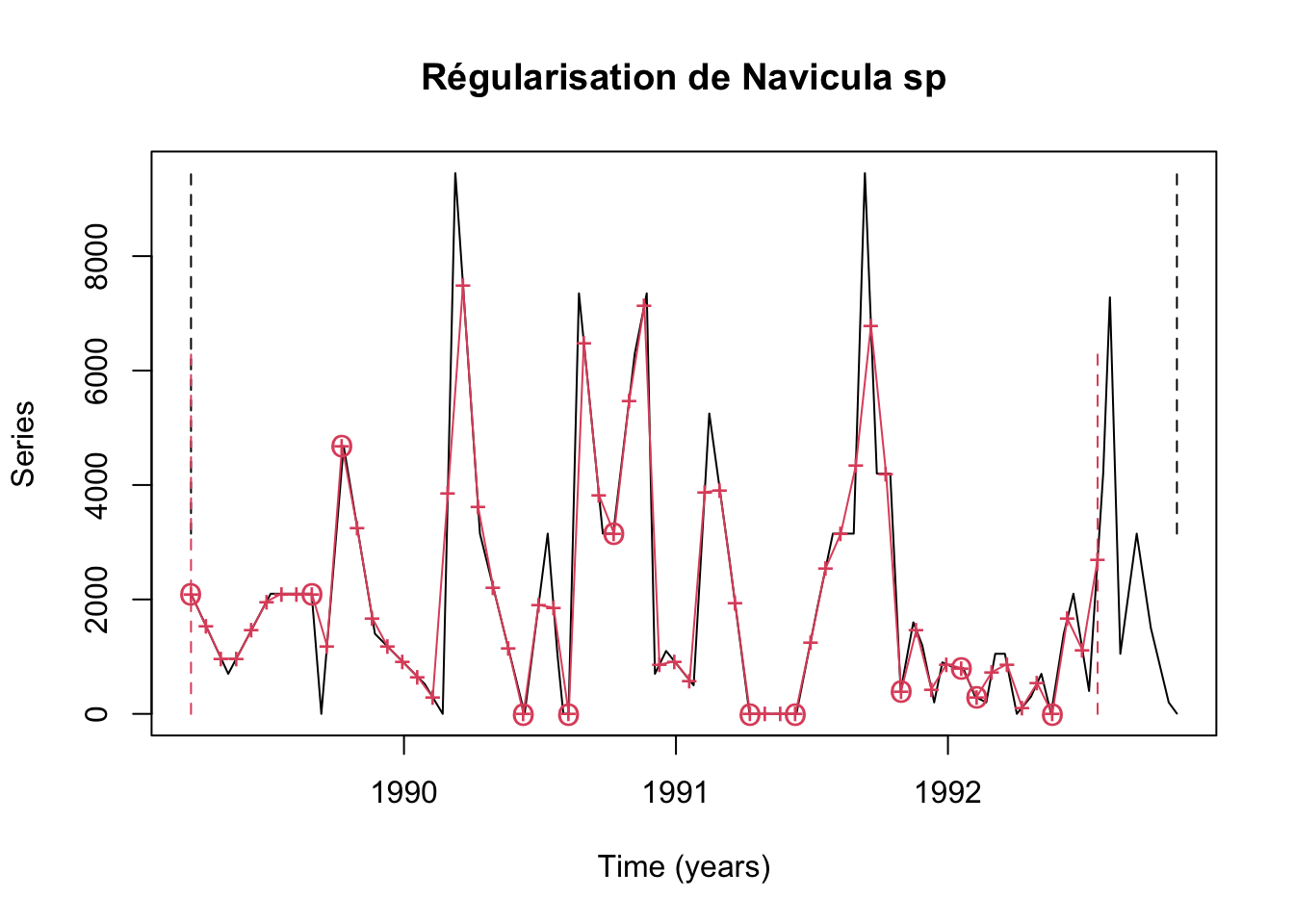
Le travail n’est pas trop mauvais … sauf que nous avons tronqué notre série à la fin. En effet, nous avons pris le même nombre d’observations que la série de départ. Comme le pas de temps de la série finale régularisée est plus court de presque deux jours que la moyenne du pas de temps dans la série irrégulière, nous perdons à droite. Il suffit de donner une valeur plus élevée pour n =, sans toutefois dépasser la date finale de la série de départ pour corriger ce léger problème :
navi_reg <- regul(releve$Day, releve$Navi, n = 66,
units = "daystoyears", frequency = 18, tol = 2.2, methods = "linear",
datemin = "21/03/1989", dateformat = "d/m/Y")# A 'tol' of 2.2 in 'days' is 0.00602327173169062 in 'years'
# 'tol' was adjusted to 0.0061728395061728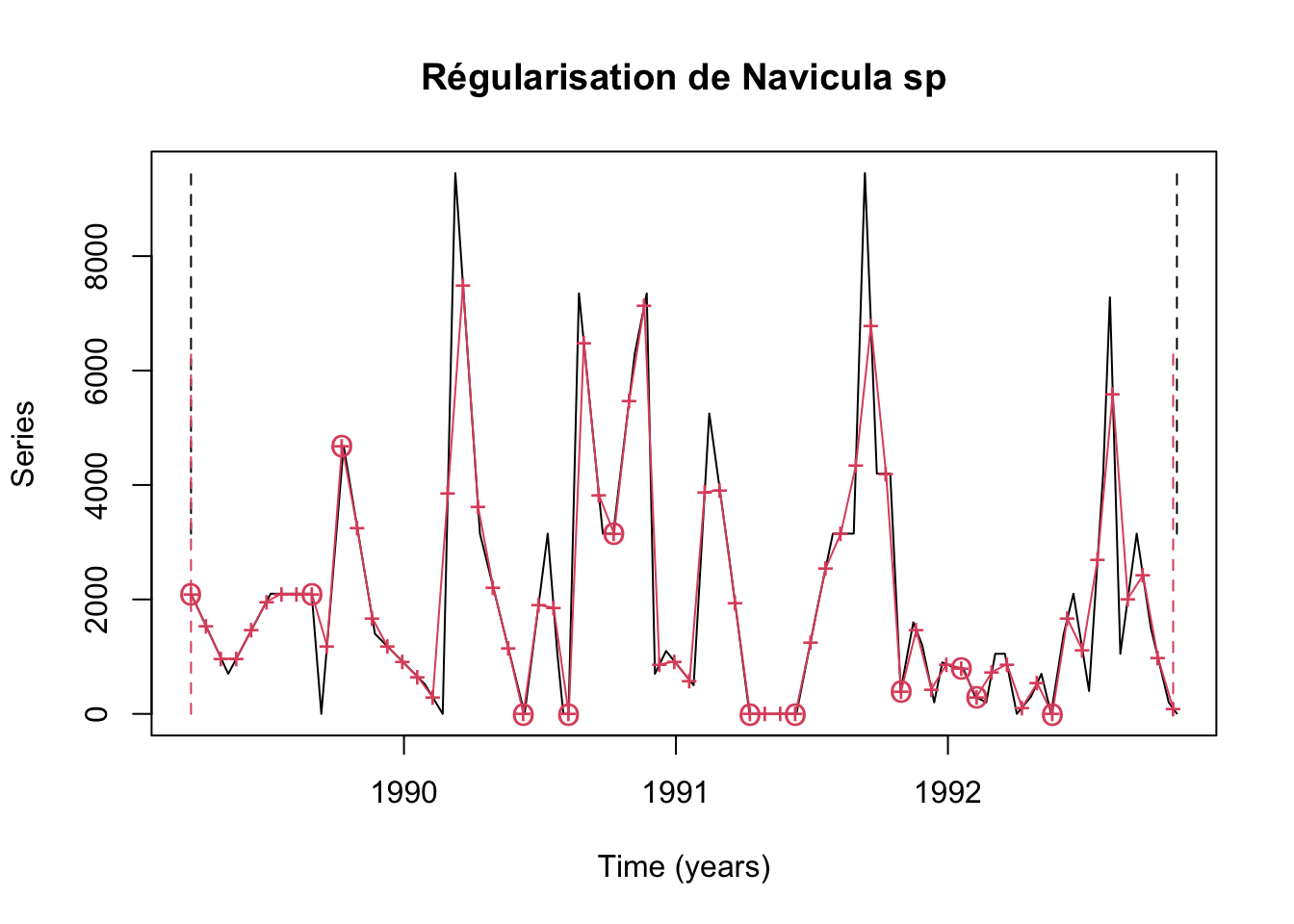
Les pics et les creux dans la série régularisée (en rouge) sont assez bien représentatifs de ceux dans la série de départ (en noir), même si les gros pics éphémères sont légèrement tronqués. Les crois entourées d’un cercle indiquent les points qui ne sont pas interpolés parce qu’une valeur existe dans la fenêtre de tolérance de ± 2,2 jours. Par contre, les croix seules sont des valeurs interpolées linéairement entre les deux observations réalisées de part et d’autre de la date cible. Les traits verticaux et pointillés indiquent le début et la fin de la série de départ (en noir) et régularisée (en rouge). Nous ne perdons presque rien sur l’axe temporel, tout en n’extrapolant aucune valeur en dehors de l’intervalle de temps de la série initiale. C’est donc parfait.
L’extraction de la série régularisée à partir de l”objet regul() se fait exactement comme pour tsd() avec tseries(), ou alors avec extract() dans le cas où plusieurs séries auraient été régularisées simultanément, mais que nous ne voulons convertir qu’une partie d’entre elles en objet ts ou mts.
# [1] "ts"# [1] 1989.167 1992.778 18.000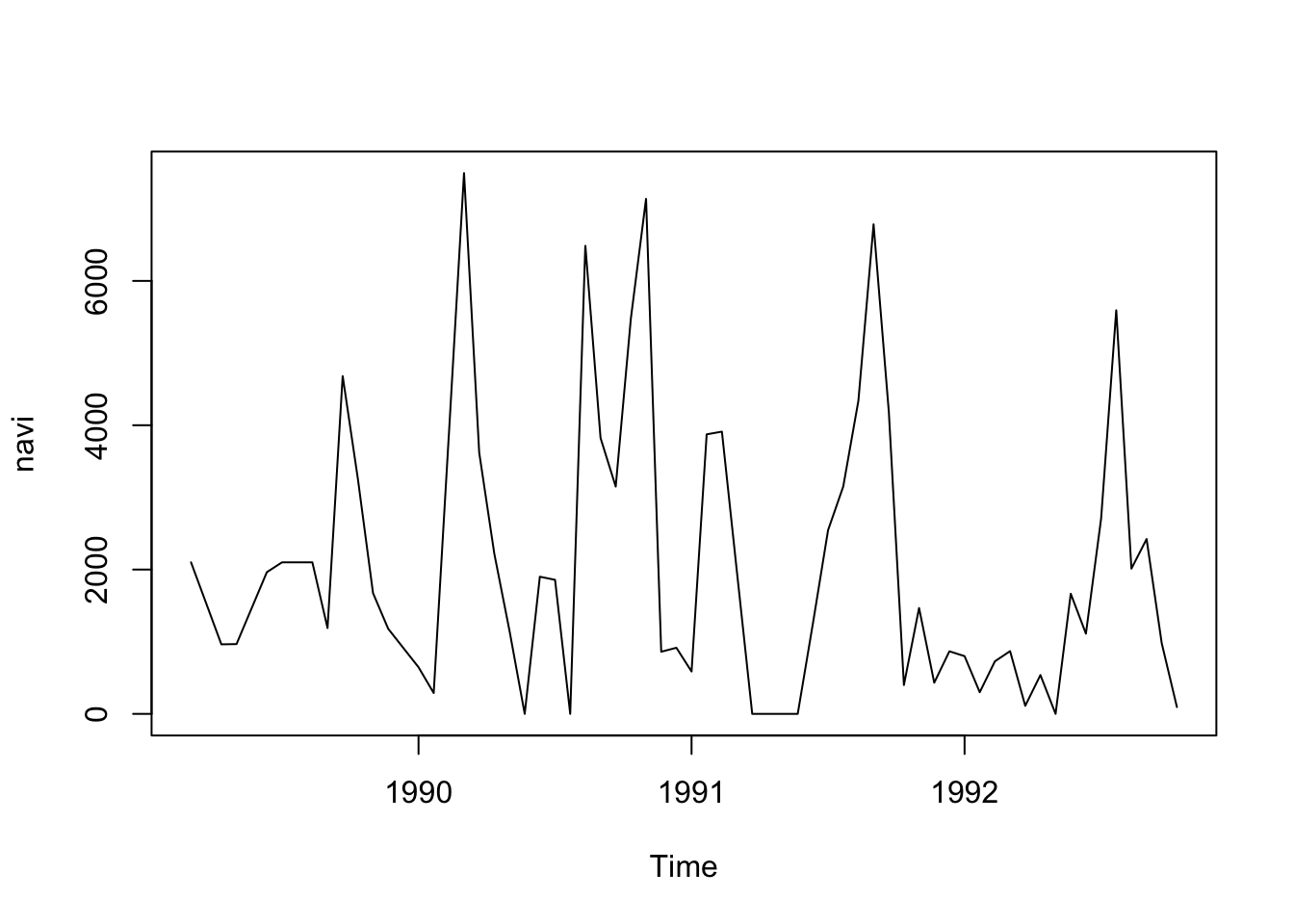
Comme nous pouvons le constater, nous avons à présent une série régulière que nous pouvons travailler avec les outils habituels !