7.1 Dates

La gestion du temps et les variables de temps peuvent sembler simples d’apparence. Nous pouvons facilement déterminer la date et l’heure qu’il est en regardant un calendrier et une montre.

À vous de jouer !
h5p

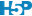
Si l’on tient compte du calendrier grégorien, des fuseaux horaires, du temps universel coordonné, de l’heure d’été …. On s’aperçoit que le temps est complexe.

Le calendrier grégorien est le calendrier le plus utilisé actuellement dans le monde. Ce calendrier défini qu’une année comprend 4 trimestres et 12 mois. Les mois varient en longueur entre 28 et 31 jours. Une semaine comprend 7 jours. Une année comprend 365 jours à l’exception des années bissextiles qui en comptent 366. Si vous n’avez pas mal de tête, on continue.

Les fuseaux horaires ont eu pour objectif de définir une heure commune pour un espace géographique déterminé. C’est l’utilisation de chemin de fer qui a rendu la mise en place d’une heure commune indispensable.

En pratique, une échelle de temps est utilisée comme référence par la majorité des pays du globe. Il s’agit du temps universel coordonné (UTC, coordinated universal time). Le terme GMT était utilisé précédemment. Il signifiait Greenwich Mean Time. À ce temps de référence, on va ajouter ou soustraire un nombre entier (avec des exceptions comme dans tout système avec l’ajout ou la soustraction d’un nombre entier plus 30 ou 45 minutes).

UTC est un compromis entre le temps atomique international et temps universel. Il faut savoir que le temps universel coordonné est synchronisé avec la rotation de la Terre qui n’est pas fixe. Le service international de la rotation terrestre et des systèmes de référence décide de l’ajout de seconde, une seconde intercalaire (leap second) à UTC comme le premier janvier 2009.

Fuseaux horaires usuels.
Fuseaux horaires usuels.

Après avoir lu ces quelques notions, pensez-vous toujours que le temps est simple ?

Comment le temps est-il géré dans R ? On retrouve les principaux objets suivants dans R pour gérer les temps : Date, POSIXct, POSIXlt, difftime. Le package {lubridate} propose en plus des objets Period.

L’objet Date va s’intéresser au temps exprimé en jours, mois et années. Le jour 0 d’un objet Date est par convention le 1970-01-01. Il s’agit de l’heure Unix (mais nous ne détaillerons pas cette notion).

library(lubridate)

(date <- as_date(now()))
# [1] "2024-03-19"
class(date)
# [1] "Date"

L’objet POSIXt compte l’heure en plus de la date. On retrouve deux variantes des objets POSIXt qui sont POSIXct et POSIXlt. Le POSIXct enregistre le temps depuis l’origine qui est l’heure Unix alors que le POSIXlt utilise une liste avec l’année, le mois, le jour, les heures, les minutes et les secondes (entre autres).

(datetime <- now())
# [1] "2024-03-19 08:26:59 CET"
class(datetime)
# [1] "POSIXct" "POSIXt"

Avec unclass(), nous pouvons voir comment un objet particulier est encodé.

unclass(datetime)
# [1] 1710833219
# attr(,"tzone")
# [1] ""

Si nous convertissons en POSIXlt, nous obtenons :

datetime2 <- as.POSIXlt(datetime)
datetime2
# [1] "2024-03-19 08:26:59 CET"
unclass(datetime2)
# $sec
# [1] 59.42901
# 
# $min
# [1] 26
# 
# $hour
# [1] 8
# 
# $mday
# [1] 19
# 
# $mon
# [1] 2
# 
# $year
# [1] 124
# 
# $wday
# [1] 2
# 
# $yday
# [1] 78
# 
# $isdst
# [1] 0
# 
# $zone
# [1] "CET"
# 
# $gmtoff
# [1] 3600
# 
# attr(,"tzone")
# [1] ""     "CET"  "CEST"

Les objets difftime sont des objets spécifiques aux différences entre deux dates.

(diff <- today() - ymd("1979-10-14"))
# Time difference of 16228 days
# Seconde manière de calculer une différence entre deux dates
diff1 <- difftime(today(), ymd("1979-10-14"))
diff == diff1 # diff et diff1 sont identiques
# [1] TRUE
class(diff)
# [1] "difftime"

7.1.1 Conversion d’une chaîne de caractères en date

En pratique vous serez souvent amené à convertir des chaînes de caractères en variable de temps. Pour ce faire, le package {lubridate} offre des fonctions très utiles pour convertir des chaînes de caractères en dates. Regardez par vous-même pour en déduire la logique simple ci-dessous :

  • Les dates :
ymd("2015-Jan-25")
# [1] "2015-01-25"
mdy("01/25/15")
# [1] "2015-01-25"
À vous de jouer !
h5p
  • Les heures :
hm("01:10 am")
# [1] "1H 10M 0S"
hms("20/10:01")
# [1] "20H 10M 1S"
hms("20:10:01")
# [1] "20H 10M 1S"
  • Les dates et heures :
ymd_hm("2010-10-01T2010")
# [1] "2010-10-01 20:10:00 UTC"
ymd_hms("2015-Jan-25 12:25:35")
# [1] "2015-01-25 12:25:35 UTC"
À vous de jouer !
h5p

Par défaut {lubridate} utilise le temps universel coordonné UTC. Il est cependant possible de définir le fuseau horaire avec l’argument tz=.

ymd_hms(now(), tz = "Europe/Brussels")
# [1] "2024-03-19 08:26:59 CET"

Ces fonctions sont capables de gérer des formats de dates différentes en même temps. Essayez cependant d’éviter ce genre d’erreur d’encodage.

ymd_hms(c("2015-Jan-25 12:25:35", "2015-01-15T122535", "2015/01/25 12:25:35"),
  tz = "Europe/Brussels")
# [1] "2015-01-25 12:25:35 CET" "2015-01-15 12:25:35 CET"
# [3] "2015-01-25 12:25:35 CET"
Plus de détails…

Pour avoir plus de flexibilité, il est possible d’utiliser la fonction parse_date_time() qui va permettre de spécifier des formats spécifiques.

  • Année
    • %Y : 4 chiffres
    • %y : 2 chiffres
  • Mois
    • %m : 2 chiffres
    • %b : nom abrégé
    • %B : nom complet
  • Jour
    • %d : 2 chiffres
  • Heure
    • %H : 0-23h
    • %i combiné avec %p : 0-12 suivi am/pm
    • %M : minutes
    • %S : secondes entières
    • %OS : secondes réelles
    • %Z : fuseau horaire
    • %z : décalage par rapport à UTC : +0100 (plus 1h)
  • Valeurs à ignorer
    • %. : ignore des caractères non numériques
    • %* : ignore une suite de caractères non numériques

Vous serez un jour confronté à un tableau de données comme suit avec plusieurs colonnes qui renseigne sur le temps de la prise de mesure.

(df <- dtx(
  annee = c(2010, 2011, 2012, 2013),
  mois  = c(01, 01, 01, 01),
  jour  = c(01, 01, 01, 01)
))
# # A data.table: 4 x 3
#   annee  mois  jour
#   <dbl> <dbl> <dbl>
# 1  2010     1     1
# 2  2011     1     1
# 3  2012     1     1
# 4  2013     1     1

Rassurez-vous, il n’est pas nécessaire de combiner les trois colonnes puis de les transformer en variable temporelle. La fonction make_date() permet de créer une variable qui combine nos trois colonnes. Il existe la même variante pour make_datetime().

(df2 <- smutate(df, date = make_date(annee, mois, jour)))
# # A data.table: 4 x 4
#   annee  mois  jour date      
#   <dbl> <dbl> <dbl> <date>    
# 1  2010     1     1 2010-01-01
# 2  2011     1     1 2011-01-01
# 3  2012     1     1 2012-01-01
# 4  2013     1     1 2013-01-01

7.1.2 Temps biologique

Lorsque vous étudiez un phénomène biologique, il faut vous poser la question de la temporalité de votre expérience.

Est-ce que votre expérience dure quelques heures ? Quelques jours ? Quelques mois ? Plusieurs années ?

Cette question est cruciale pour traiter vos données. Prenons trois petits cas pratiques.

  • La croissance de coraux sur 30 jours

Vous réalisez une expérience sur la croissance d’une espèce de corail durant 30 jours en aquarium. Cette expérience débute le 20 septembre 2019. Voici deux représentations graphiques possibles selon que vous indiquez les dates ou le temps écoulé depuis le début de l’expérience :

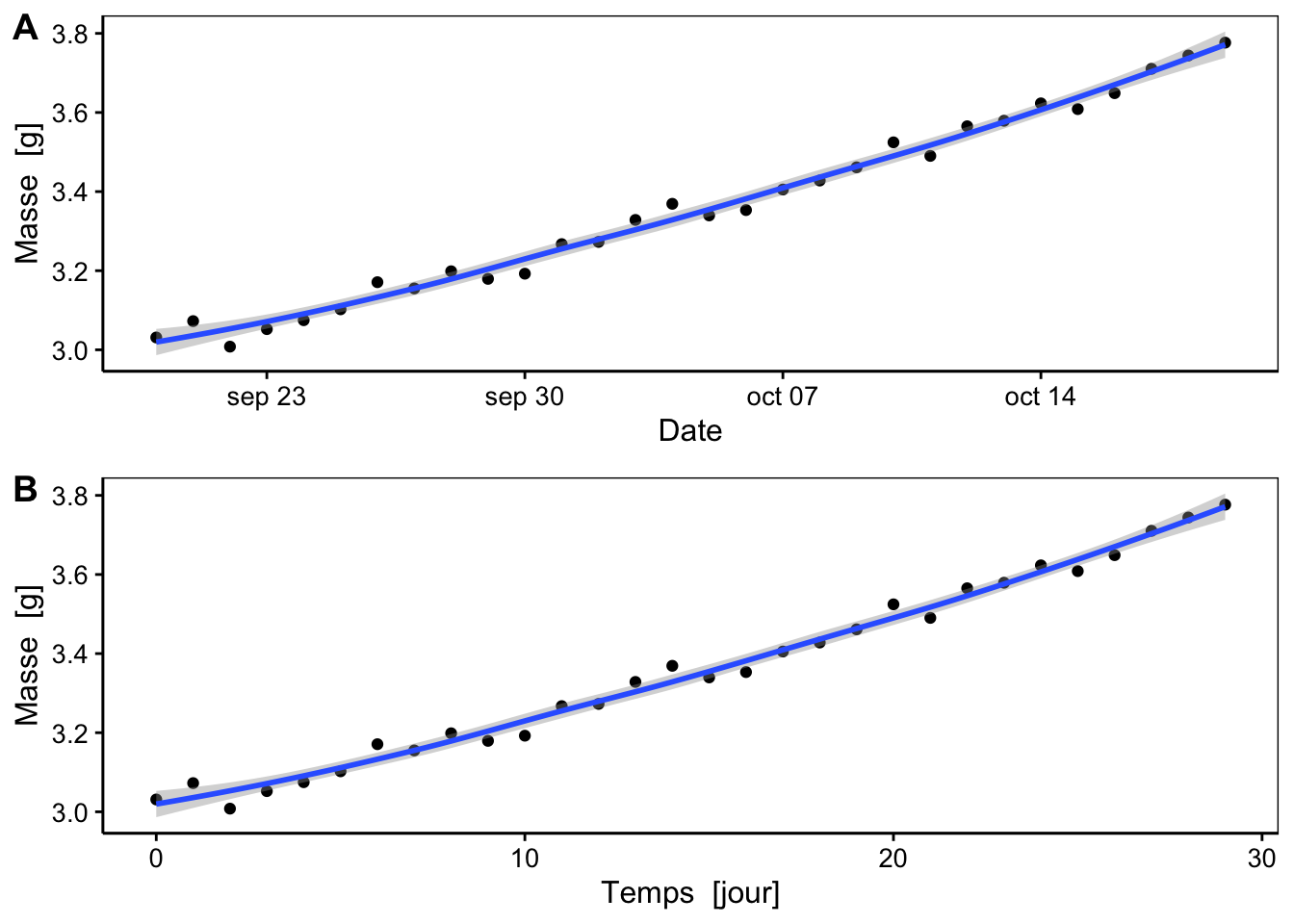
On comprend rapidement que le second graphique est plus intéressant. Il n’est pas nécessaire de connaitre les dates précises lorsque l’on étudie la croissance d’un organisme en aquarium sur 30 jours.

  • Le temps perdu dans les embouteillages

Lorsque l’on étudie le temps perdu dans les bouchons à Bruxelles. Il sera très important de spécifier les jours de la semaine. En effet, nous savons que les bouchons vont varier entre la semaine ou le weekend ou encore lors d’un jour férié. On ne peut donc pas se passer d’une date précise lorsque l’on étudie ce genre de phénomène.

  • L’évolution de la température sur 20 ans

Lorsque l’on étudie des séries temporelles en écologie, on ne s’intéresse pas aux années bissextiles, ou aux mois de 29 ou 31 jours.

Dans R avec les objets ts et mts nous avions vu au module 4 et module 5 du cours de science des données 3. Avec ces objets, le temps est décompté de manière décimale dans une unité arbitraire que vous avez décidée. Le package {pastecs} reprend ce principe. Ainsi, si vous étudiez un phénomène saisonnier, vous allez naturellement choisir l’année comme unité. Par contre, décompter le temps en années de manière décimale n’est pas très conforme au calendrier grégorien, aux mois de durées différentes et aux années bissextiles. Par contre, la plupart des phénomènes biologiques (naturels) que vous étudiez se soucient assez peu du calendrier grégorien. Leurs rythmes sont calqués plutôt sur les saisons, les journées, les cycles lunaires ou de marées, etc. L’utilisation de valeurs numériques, quitte à tordre un peu les choses par rapport calendrier grégorien (donc à avoir des années ou des mois qui commencent et finissent jusqu’à un jour plus tôt ou plus tard) est alors pratique ici. Ainsi, considérer une année moyenne (considérant les années bissextiles) comme étant égale à 365,25 jours et un mois comme étant 365,25/12 est bien plus pratique ici. Le tableau ci-dessous représente le temps dans ce système.

Temps Période Longueur (j)
année 1 365,25
trimestre 4 365,25/4 = 91,31
mois 12 365,25/12 = 30,44
semaine 52 365,25/52 = 7,02
jour 365 365,25/365 = 1,00

En biologie, on va s’intéresser principalement à des cycles particuliers comme le cycle circadien, la succession des saisons, le cycle lunaire … que l’on pourra réexprimer dans cette échelle décimale en n’effectuant pas une approximation supérieure à un jour par rapport à notre décompte des jours dans le calendrier.

Pour en savoir plus
À vous de jouer !

Réalisez le travail D07Ia_data, partie I.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie I.