4.4 Analyse de séries

Les différentes techniques présentées dans cette section permettent de caractériser des séries spatio-temporelles, que ce soit en analysant l’autocorrélation ou la cross-corrélation, en effectuant une analyse spectrale, ou en déterminant l’existence d’une tendance générale ou locale. Le module suivant traitera plus particulièrement de la décomposition de séries en plusieurs composantes (tendance, cycle saisonnier, résidus par exemple). Bien que la décomposition et l’analyse soient des phases du traitement des séries spatio-temporelles qui ne se font pas l’une sans l’autre, nous les traitons dans des chapitres différents parce qu’elles renvoient des résultats différents. Alors que les techniques d’analyse ne modifient pas la série de départ et renvoient seulement les résultats statistiques de l’analyse, les décompositions renvoient des objets plus complexes qui contiennent aussi les composantes issues du traitement, composantes qui peuvent être transformées à nouveau en objets ts ou mts pour être traitées ou analysées en cascade éventuellement.

4.4.1 Autocorrélation, autocovariance, cross-corrélation et cross-covariance

Une série spatio-temporelle est caractérisée principalement par une autocorrélation non nulle, nous l’avons déjà vue, ce qui signifie que les différentes observations dans la série ne sont pas indépendantes les unes des autres. Cette autocorrélation s’étudie en considérant le profil de la fonction d’autocorrélation L’autocorrélation sera d’autant plus grande que les deux séries (initiale et décalée) sont similaires. À l’inverse, si les séries sont opposées, l’autocorrélation sera négative. Une autocorrélation nulle indique qu’il n’y a pas de corrélation entre la série initiale et la série décalée au pas considéré. Le graphique de l’autocorrélation (caractéristique d’une série périodique) pour notre série artificielle tser est obtenu par la fonction acf() :

tser <- ts(sin((1:100) / 6 * pi) + rnorm(100, sd = 0.5), start = c(1998, 4),
  frequency = 12)
acf(tser)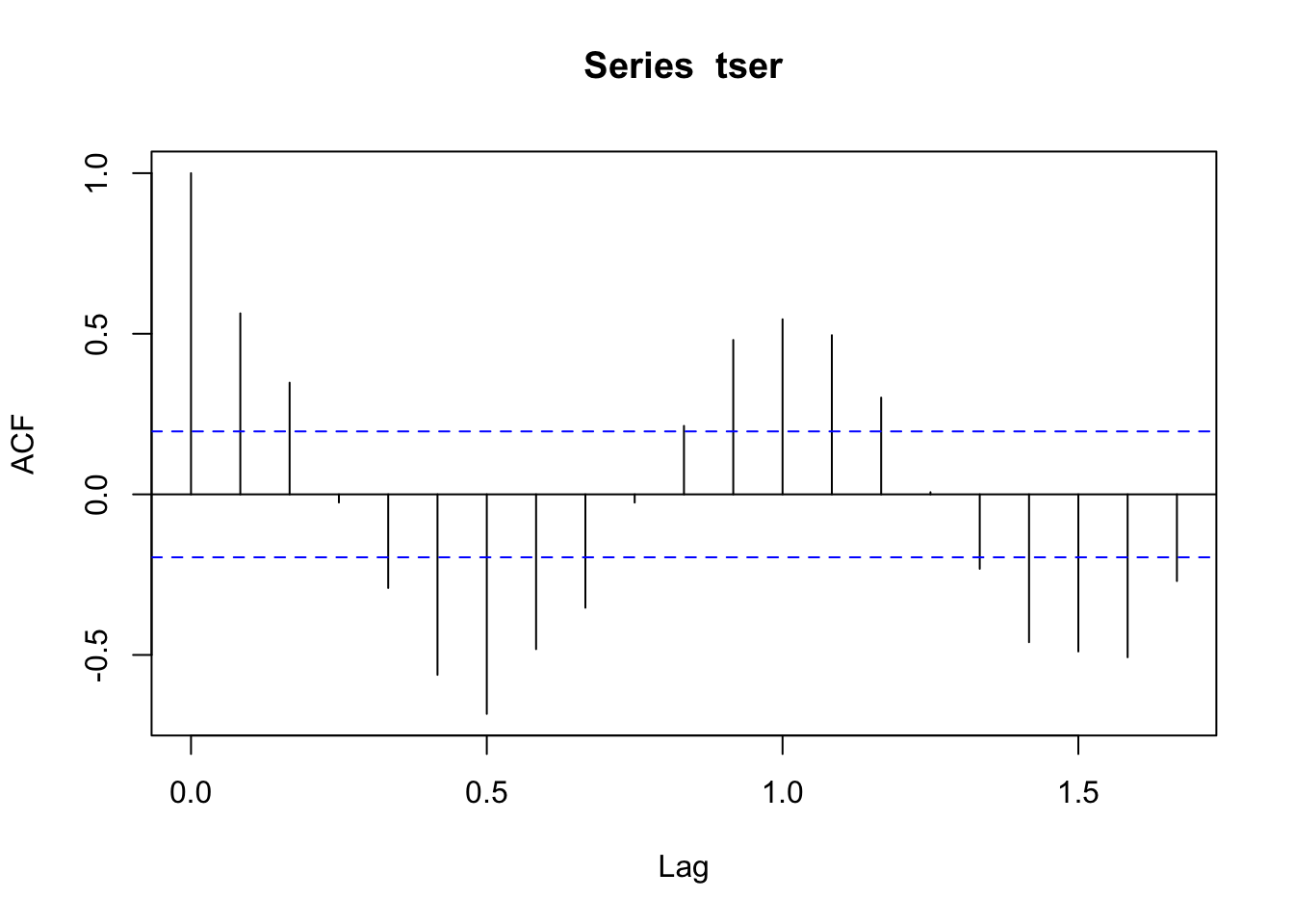

Pour un décalage nul, la première barre verticale monte jusqu’à un toujours. Les barres suivantes montrent jusqu’où l’effet mémoire de la série se marque. Les traits bleus horizontaux représentent une enveloppe de confiance à 95%. Donc, les barres qui dépassent (largement) de l’intervalle entre ces deux traits bleus sont significatives. Nous voyons ici que l’effet mémoire se marque sur les deux mois qui suivent (2 barres au-dessus du trait bleu). Ensuite, le graphique est caractéristique d’une série périodique. En effet, l’autocorrélation passe par un minimum lorsque la série est décalée d’une demi-période. Ici, le cycle a une période d’un an. Nous voyons que nous passons par une autocorrélation négative et minimale après un décalage de 6, puis de 18 mois. L’axe des abscisses Lag est exprimé dans l’unité de la série qui est l’année ici. Cela correspond donc à respectivement 0.5 et 1.5 unité. Par contre, l’autocorrélation redevient positive et maximale pour un décalage d’une période exactement ou d’un multiple de cette période. Ainsi, nous avons un mode pour un décalage de 1 année. Nous étudierons juste en dessous une technique plus puissante pour détecter les cycles dans une série (analyse spectrale), mais lorsqu’ils sont flagrants comme ici, ils sont également clairement visibles sur le graphique de l’autocorrélation.

Pour un bruit blanc (une série constituée d’observations indépendantes les unes des autres), l’autocorrélation doit être nulle. Générons artificiellement une telle série afin de visualiser le graphique de l’autocorrélation correspondant :

set.seed(1358) # Initie le générateur de nombre pseudo-aléatoires
white_noise <- ts(rnorm(100))
plot(white_noise)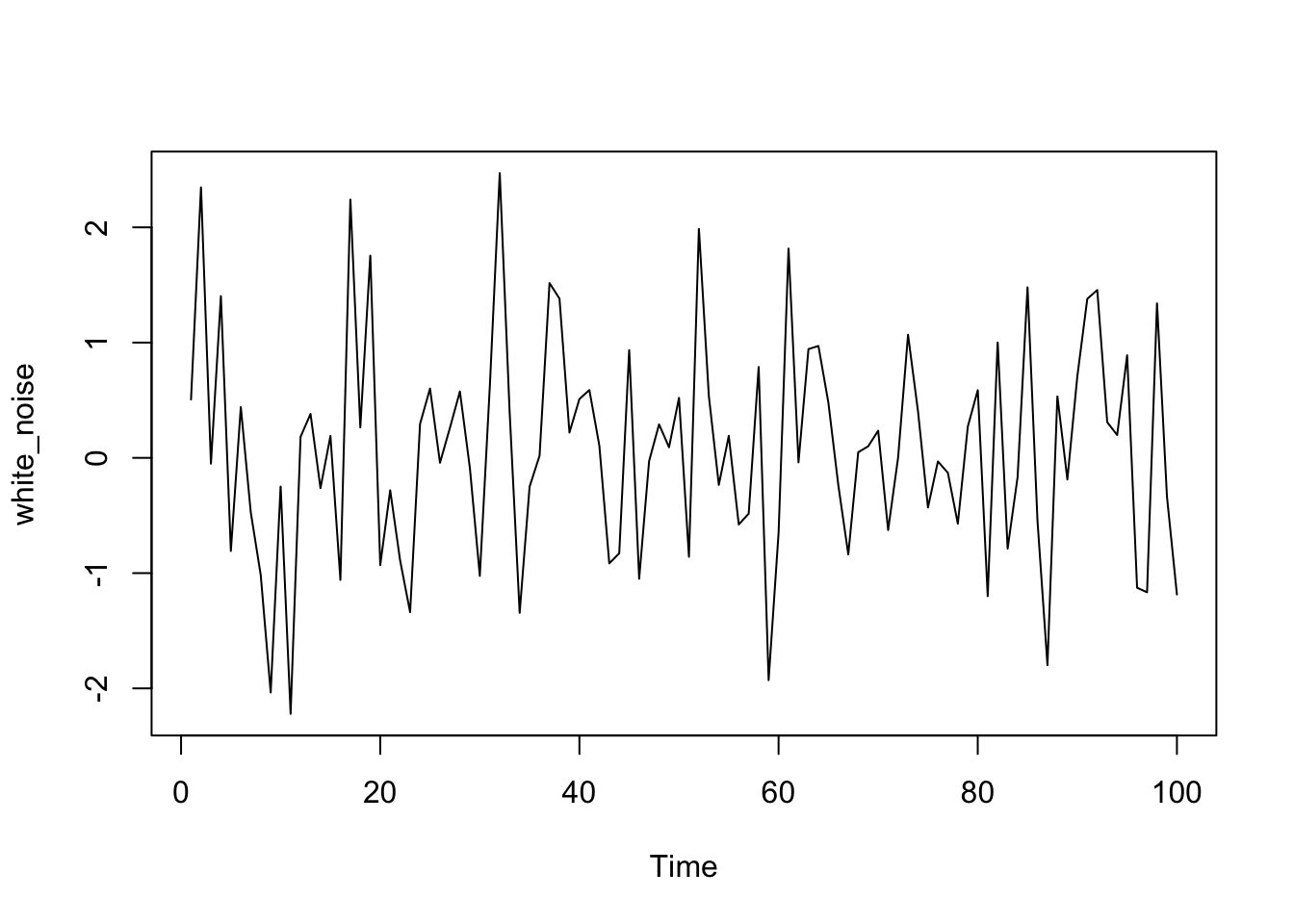

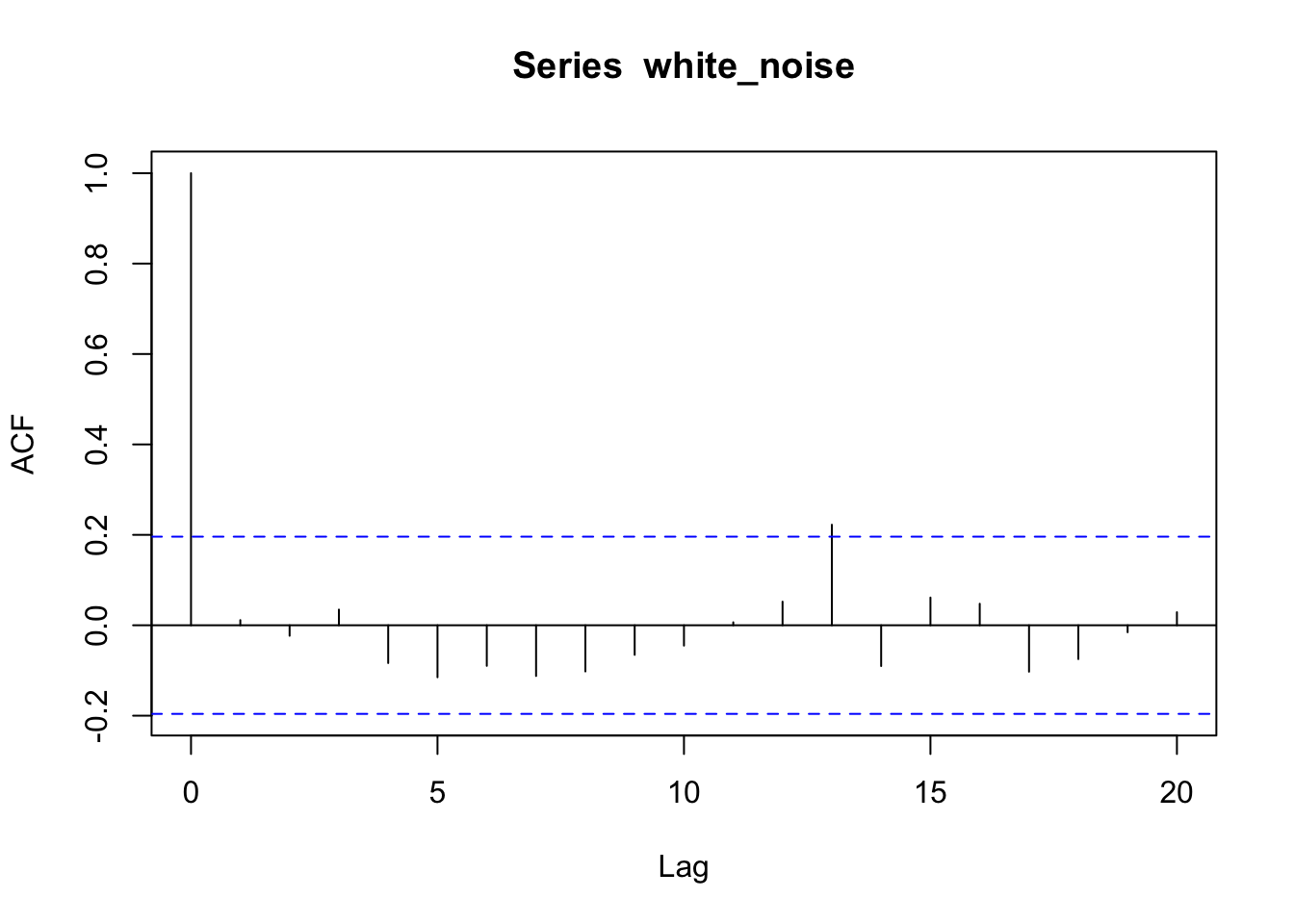
acf(white_noise)

Effectivement, pratiquement toutes les barres sont comprises à l’intérieur de l’enveloppe de confiance à 95%. Il est normal que 5% des barres sortent de cette enveloppe. À part la première pour un décalage nul qui ne doit pas être comptabilisé, nous avons une barre qui sort très légèrement sur 20, soit 5% (il pourrait aussi y en avoir deux ou trois, ou bien zéro au contraire par le biais du hasard, sans que cela change nos conclusions). Ce type de graphique doit nous diriger immédiatement vers la conclusion que l’autocorrélation est nulle ou négligeable dans la série.

Si le graphique de la fonction d’autocorrélation a des barres qui sont toutes positives et significatives, cela signifie probablement qu’une tendance générale à l’augmentation domine le signal (elle est alors déjà bien souvent visible dans le graphique de la série elle-même). Si les barres sont toutes significatives et qu’il y a en plus une oscillation, nous avons alors à la fois une tendance et un cycle dont les effets sont à peu près équivalents. Le graphique de la fonction d’autocorrélation suivant est issu de la décomposition du jeu de données co2 où nous avons extrait uniquement la tendance générale (voir l’exemple de décomposition de la série co2 plus loin).

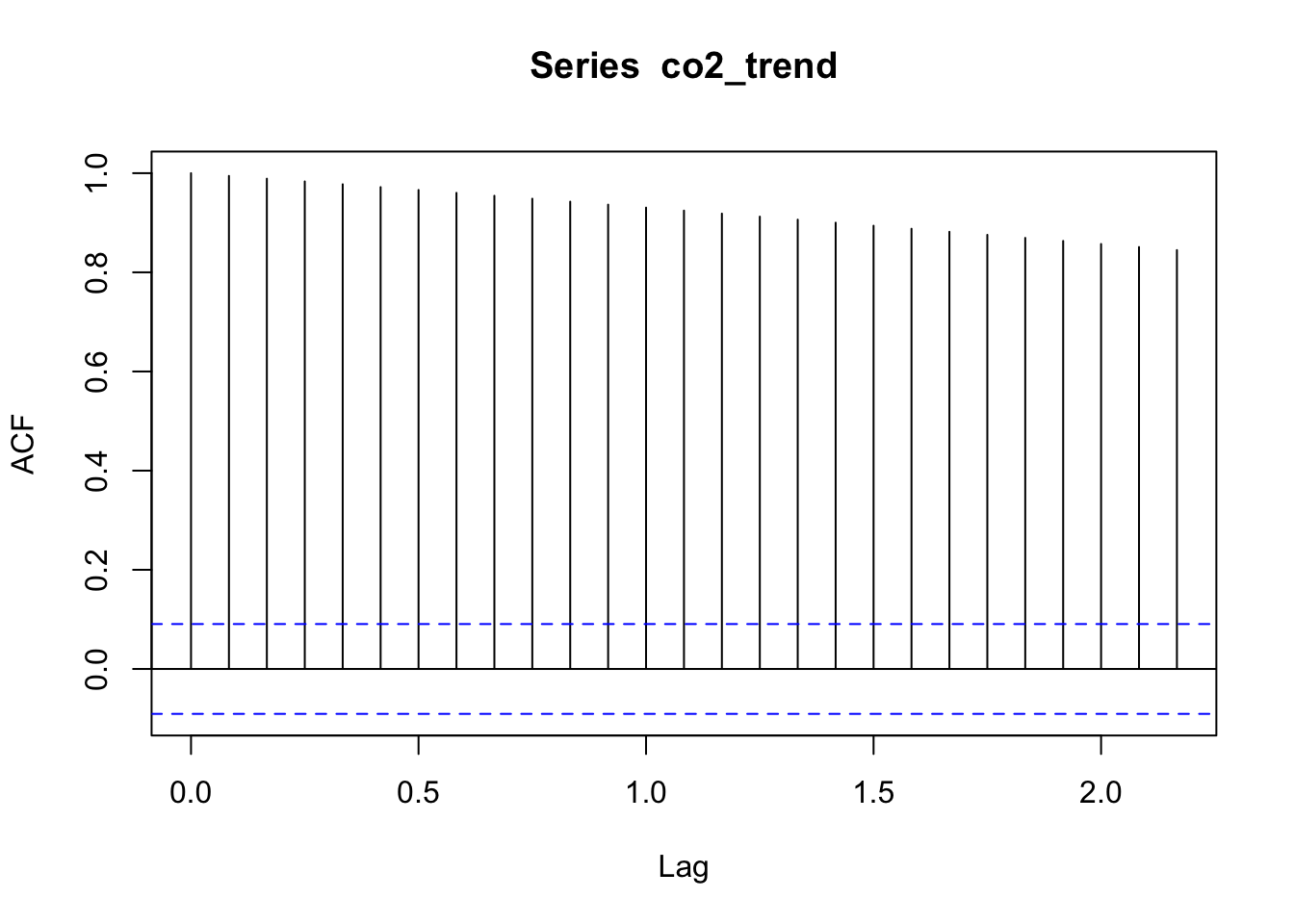
Bien que nettement moins utilisé en pratique, on peut également tracer le graphique de l’autocovariance (la covariance est calculée entre la série de départ et la série décalée à la place de la corrélation) en précisant l’argument type = "covariance" à l’appel de acf(). On a aussi la possibilité de calculer une autocorrélation partielle avec type = "partial". En outre, R fournit également ccf(), fonction qui calcule la cross-corrélation (ou corrélation croisée) ou la cross-covariance entre deux séries. Ceci peut s’avérer utile pour déterminer s’il y a une dépendance entre les deux séries, et éventuellement estimer également un décalage éventuel dans le temps pour cette dépendance. À titre d’illustration, prenons notre série artificielle tser et décalons-là de cinq mois. Traçons ensuite le graphique de cross-corrélation entre ces deux séries :

mtser <- ts.intersect(tser, stats::lag(tser, 5))
ccf(mtser[, 1], mtser[, 2])

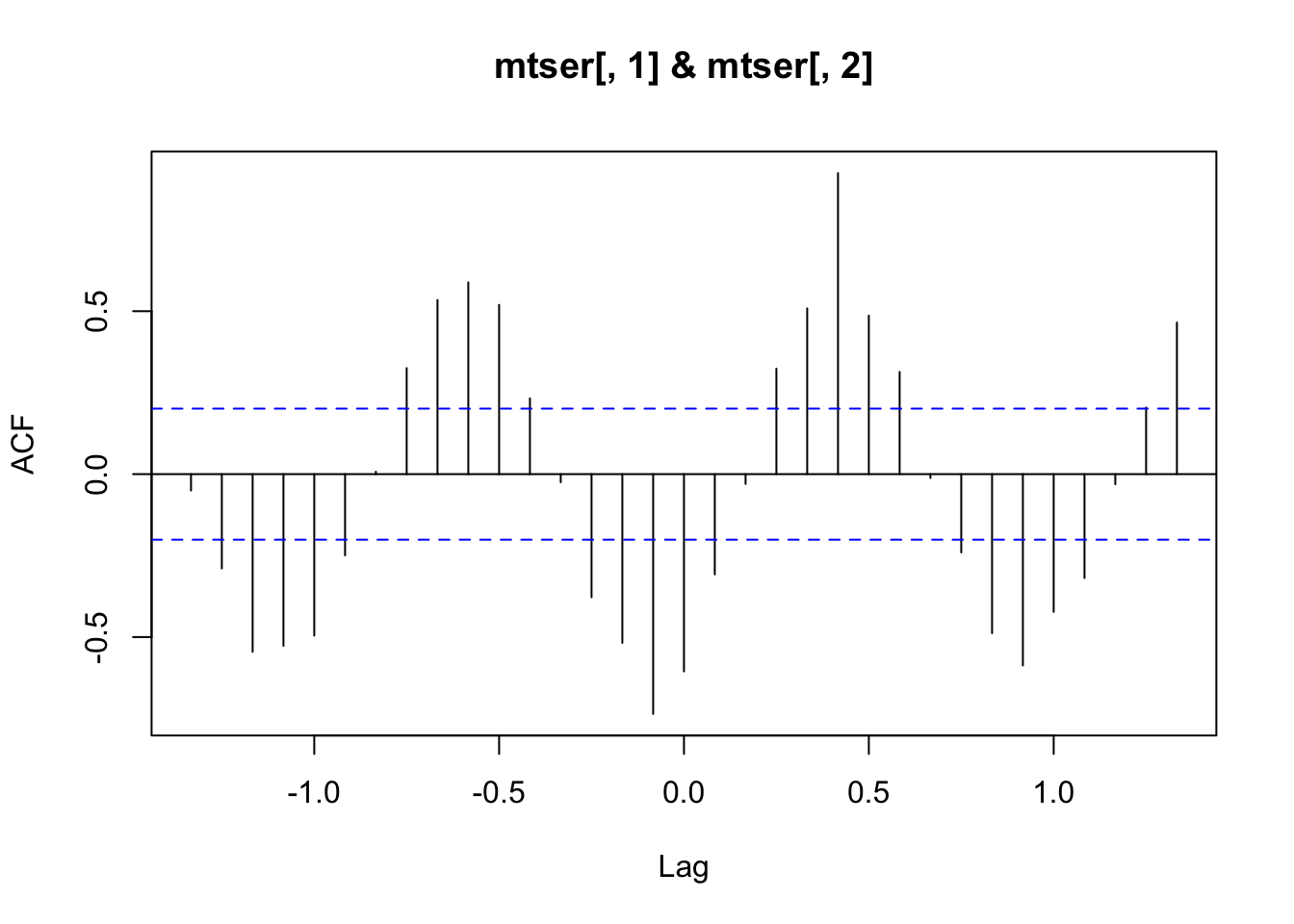
On retrouve bien une cross-corrélation maximale pour un décalage de cinq entre la série de départ (mtser[, 1]) et la série décalée (mtser[, 2]) : à partir du zéro, c’est la cinquième barre vers la droite qui est la plus élevée. Nous retrouvons également l’alternance entre corrélation positive et négative caractéristique de signaux cycliques sur ce graphique.

Exercez-vous

Si vous voulez affiner votre compréhension du graphique de l’autocorrélation, générez et examinez ces graphiques pour nos différentes séries d’exemples. Les séries lynx et co2 doivent certainement présenter une variation périodique claire, mais pour co2, une tendance générale forte se superpose. Les autres séries sont moins claires sur le graphique obtenu avec plot()… que pouvez-vous observer sur le graphique de l’autocorrélation ?

Pour en savoir plus

• Aide en ligne de ?acf et ?plot.acf pour les différents arguments utilisables.

• Manuel de {pastecs} en ligne, en français, outre la section concernant l’autocorrélation dont la présente partie s’inspire très largement, une section est également dévolue à l’autocorrélation multiple et à son utilisation pour la détection de transitions dans une série.

4.4.2 Analyse spectrale

Afin d’identifier de manière fine les composantes cycliques d’une série chronologique, nous pouvons considérer que cette série est la combinaison d’un ensemble de signaux (co)sinusoïdaux de fréquence croissante. Pour rappel, la période d’un signal cyclique est le temps nécessaire pour accomplir exactement un cycle. Par contre, la fréquence, notée oméga (\(\omega\)) est l’inverse de de cette période \(\omega = 1/période\), et cela correspond au nombre de cycles qui rentrent dans une unité de temps exactement (pour rappel, vous choisissez librement l’unité ici, année, quadrimestre, mois, jour, minute, seconde… millénaire, etc.). Un signal périodique élémentaire peut s’écrire alors à l’aide d’une fonction cosinus à trois paramètres : outre la fréquence \(\omega\), il y a l’amplitude du signal notée \(A\) et la phase phi (\(\phi\)) qui définit où le cycle commence sur l’axe du temps. Cette phase est un peu l’équivalent de l’ordonnée à l’origine pour une droite, soit un décalage du signal sur l’axe temporel.

\[x_t = A \cdot \cos(2 \pi \omega t + \phi)\]

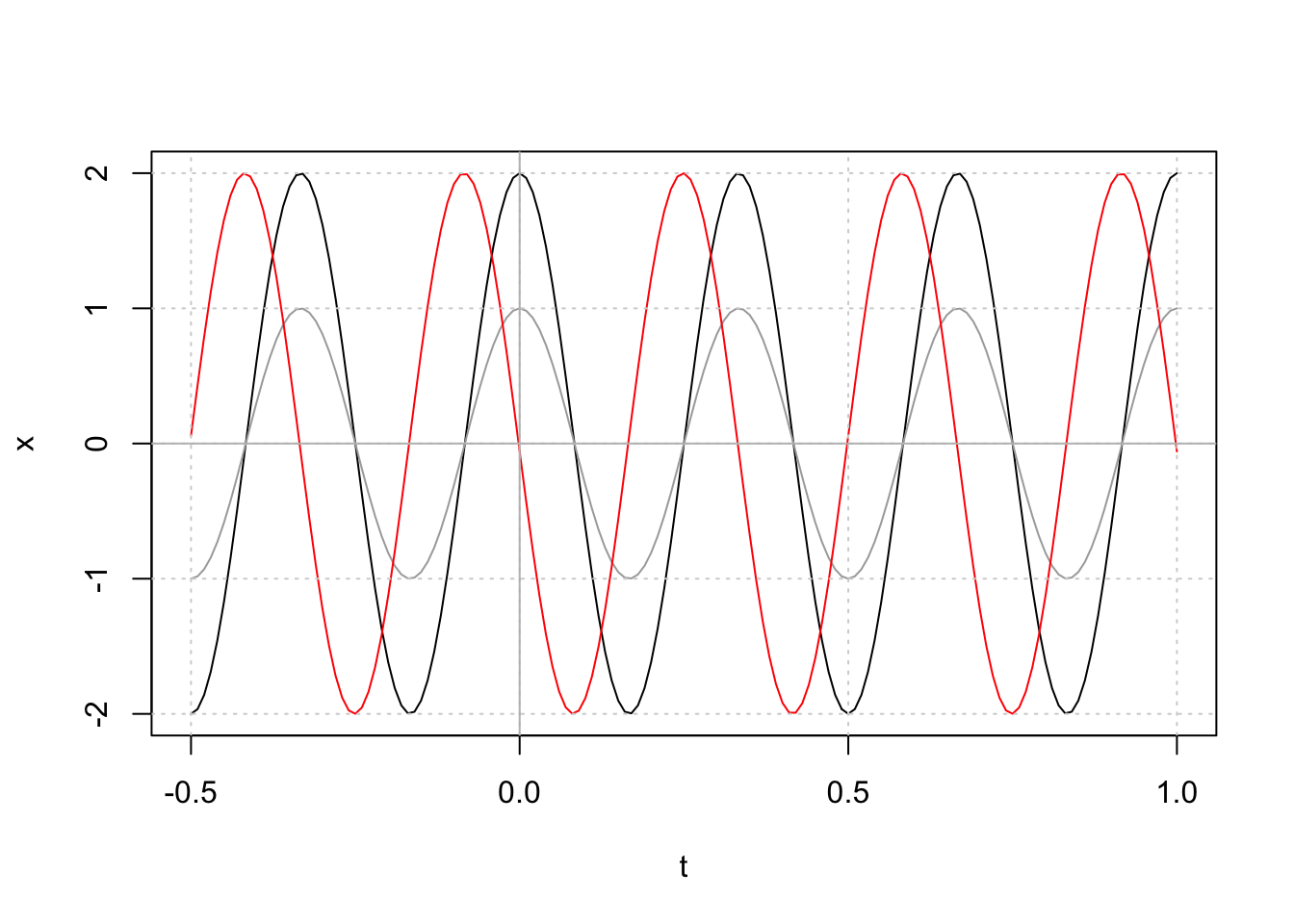
Figure 4.2: Fonction cosinus avec une fréquence de 3. En gris, amplitude = 1, phase = 0. En noir, amplitude = 2, phase = 0. En rouge, amplitude = 2, phase = 1.6.

Sur le graphique nous avons représenté trois cosinusoïdes pour vous illustrer l’effet des trois paramètres.

• Avec \(\omega\) = 3, nous avons exactement trois cycles dans une unité de t, donc, trois cycles entre 0 et 1 sur l’axe des abscisses pour toutes les courbes. En faisant varier \(\omega\) on resserre ou étale les cycles sur cet axe (horizontalement).

• La courbe grise ayant une amplitude A d’un, est comprise entre +1 et -1 sur l’axe des ordonnées (étalement vertical). Les deux autres ont une amplitude A doublée de deux. Par conséquent, le signal monte et descend deux fois plus entre +2 et -2.

• Enfin, la phase \(\phi\) des courbes grises et noires étant nulle, nous passons par un maximum en zéro sur l’axe des abscisses, car cos(0) = 1 = valeur maximale. Par contre, la courbe rouge est la même que la noire, mais déphasée de 1.6, ce qui la translate sur l’axe t. Avec une phase de 1.6 qui est environ égale à \(\pi/2\), notre courbe rouge passe pratiquement par zéro pour \(x_t\) lorsque \(t = 0\).

Les mathématiciens nous apprennent que l’on peut s’affranchir de \(\phi\) à condition de considérer une somme de sinus et cosinus. Quel que soient \(A\), \(\omega\) et \(\phi\), il existe toujours une paire \(\beta_1\), \(\beta_2\) tel que :

\[A \cdot \cos(2 \pi \omega t + \phi) = \beta_1 \cdot \cos(2 \pi \omega t) + \beta_2 \cdot \sin(2 \pi \omega t)\]

En fait, \(\beta_1 = A \cdot \cos(\phi)\) et \(\beta_2 = -A \cdot \sin(\phi)\). Cette reparamétrisation nous ouvre les portes de la transformation de Fourier qui consiste à considérer un signal de forme quelconque comme une somme de sinus et cosinus de fréquences différentes. Pour \(n\) observations de \(x_t\), nous pourrons réécrire la série sous forme d’une somme de termes cycliques comme ceci :

\[x_t = \sum^{n/2}_{i = 1} \left[ \beta_{1 i} \cos(2 \pi \omega_i t) + \beta_{2 i} \sin(2 \pi \omega_i t) \right]\]

Les \(\omega_i\) représentent des fréquences croissantes que nous fixons nous-mêmes au départ. Les \(\beta_{1 i}\) et \(\beta_{2 i}\) sont des paramètres qui sont déterminés pour que l’égalité soit rencontrée. Si nous considérons \(n/2\) fréquences différentes, comme c’est le cas ici, nous avons donc \(n\) paramètres \(\beta_.\) à estimer, puisque pour chaque fréquence \(\omega_i\), nous avons deux paramètres (\(\beta_{1 i}\) et \(\beta_{2 i}\)) à estimer à chaque fois. Or, avec un même nombre de paramètres que d’observations, nous ajustons exactement le modèle constitué de sommes de sinusoïdes et cosinusoïdes à travers toutes les valeurs observées. Cette équation est, en outre, facile à résoudre numériquement sur ordinateur à l’aide d’un algorithme appelé FFT (pour Fast Fourier Transform en anglais) qui permet de calculer très rapidement tous les paramètres \(\beta_.\).

Nous arrivons à ce qui nous intéresse. L’amplitude de chaque signal de fréquence différente constituant notre série peut s’exprimer au travers de ce qu’on appelle un périodogramme \(P_i\) qui se calcule comme suit à un facteur d’échelle près :

\[P_i = \hat \beta_{1 i}^2 + \hat \beta_{2 i}^2\]

avec \(\hat \beta_{1 i}\) et \(\hat \beta_{2 i}\) qui sont les estimateurs des paramètres \(\beta_{1 i}\) et \(\beta_{2 i}\) pour les différentes fréquences \(\omega_i\) sur base de l’échantillon dont nous disposons (nos observations). Bien que la démonstration de ceci sorte du cadre de ce cours –elle fait intervenir la théorie de l’information et la probabilité d’observer un pic ou un creux dans une série à un instant t donné, ce qu’on appelle un point de retournement– il est possible d’estimer la probabilité qu’une valeur de \(P_i\) se produise dans une série non périodique. Nous pouvons dès lors en dériver un test d’hypothèse. dont l’interprétation sera la suivante : si la valeur de \(P_i\) est supérieure à un seuil défini par rapport à \(\alpha\), nous pourrons considérer qu’il existe un signal périodique significatif à la fréquence \(\omega_i\) correspondante dans notre série. Autrement dit, pour cette fréquence-là, il est très peu probable (probabilité du test < \(\alpha\)) qu’une telle amplitude de signal apparaisse par pur hasard dans la série.

L’estimation fournie par le périodogramme brut donne un diagramme très irrégulier. Pour y remédier, on divise l’intervalle des fréquences en bandes centrées autour de j fréquences équidistantes. Ensuite, on lisse le signal à l’aide d’une moyenne mobile pondérée associée à chaque bande de fréquence (nous verrons au module suivant ce qu’est une moyenne mobile, retenez simplement que c’est une technique efficace pour lisser une courbe). Le périodogramme lissé est ainsi beaucoup plus facile à interpréter, mais au prix d’une perte de résolution au niveau des fréquences, exprimée par une largeur de bande plus grande dans le périodogramme.

Exemple

Sous R, la fonction spectrum() trace à la fois le périodogramme brut et le périodogramme lissé. Ainsi, les spectres bruts et lissés de tser sont obtenus côte à côte par :

par(mfrow = c(1, 2))            # Place deux graphes côte à côte
spectrum(tser)                  # Périodogramme brut
spectrum(tser, spans = c(3, 5)) # Périodogramme lissé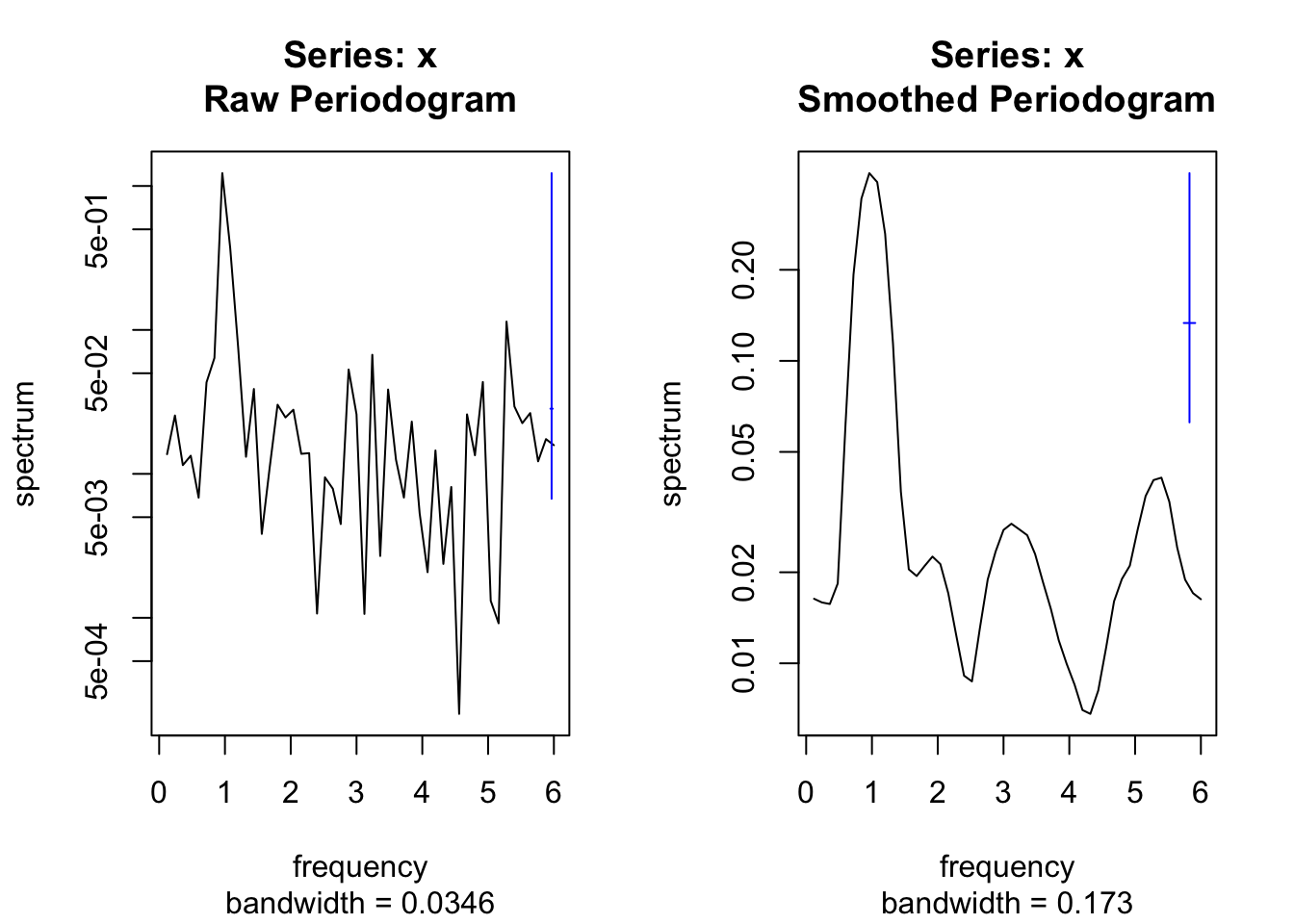

par(mfrow = c(1, 1))            # Valeur par défaut pour mfrow

Le lissage du périodogramme fait intervenir un argument spans = qui prend un vecteur de deux entiers impairs. Plus ces valeurs seront élevées, plus le lissage sera important, mais attention à ne pas tomber dans l’excès non plus. En pratique, nous pouvons tester différentes combinaisons et retenir celle qui donne visuellement le meilleur périodogramme. Notez comme le lissage a changé la largeur de bande (bandwidth en anglais) entre les deux graphiques.

Pour l’interprétation, nous nous référons à la barre bleue à droite du graphique qui matérialise la zone sur l’axe des ordonnées pour laquelle une fréquence peut être considérée comme significative d’après le test d’hypothèse associé, en utilisant \(\alpha\) = 5%. Alors que sur le périodogramme brut il peut sembler que la courbe traverse cette zone sensible un grand nombre de fois, c’est le périodogramme lissé qui nous indique de manière correcte que ces données artificielles ne comportent qu’une seule fréquence significative au seuil \(\alpha\) de 5% : la fréquence de 1. Le périodogramme brut est donc inutilisable pour identifier correctement les fréquences significatives. Nous utiliserons toujours en pratique un périodogramme lissé pour nos analyses.

R offre aussi la possibilité de représenter le périodogramme cumulé qui permet souvent d’identifier plus clairement les fréquences significatives sous forme d’un saut vertical brutal dans la courbe qui sort de l’enveloppe de confiance à 95% matérialisée par deux traits pointillés bleus (ici, le saut se fait bien à une fréquence de 1).

cpgram(tser)

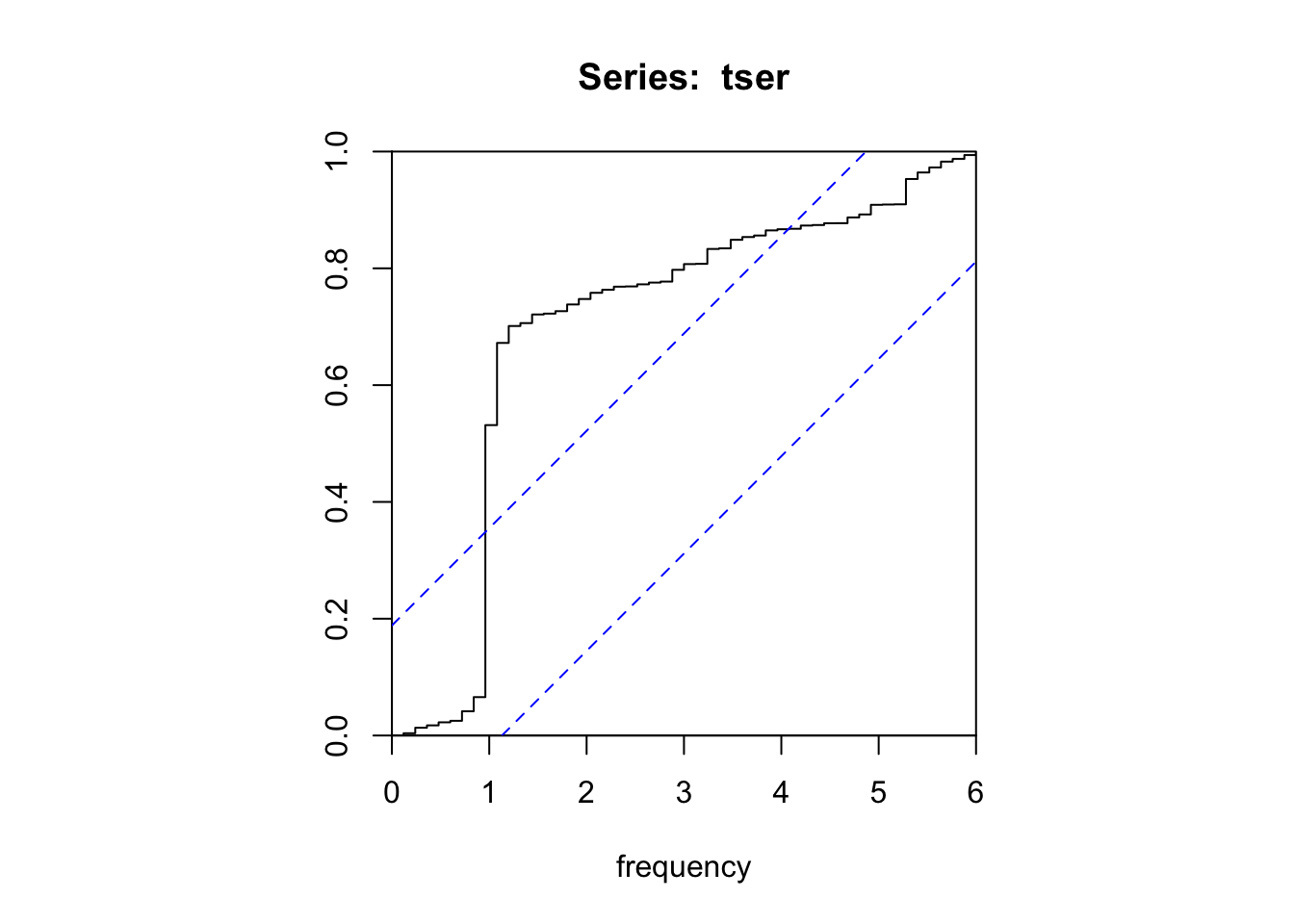
L’analyse spectrale ne peut se faire que sur une série qui ne présente pas de tendance à long terme. On parle alors de série stationnarisée. Si ce n’est pas le cas, nous devons éliminer cette tendance générale avant de faire l’analyse spectrale. Les techniques pour éliminer cette tendance générale seront vues au prochain module.

Parmi nos séries d’exemples, co2 présente une tendance générale croissante très marquée. Cette série ne peut donc pas être analysées à l’aide de spectrum() ou cpgram() telle quelle. Nous devons d’abord la stationnariser, donc éliminer sa tendance générale.

4.4.2.1 Analyse spectrale croisée

Cette partie sur l’analyse spectrale croisée est présentée sans démonstration et comme matériel complémentaire facultatif. Veuillez vous référez à l’aide en ligne en entrant l’instruction ?stats::spectrum à la console R et au manuel de {pastecs} pour plus de détails.

L’analyse spectrale peut être étendue au cas de signaux bivariés, tout comme le fait la corrélation croisée. On pourra détecter les oscillations qui sont importantes simultanément dans deux séries, tester la corrélation entre les mouvements de même période, et estimer le déphasage éventuel entre ces oscillations.

Exemple d’analyse spectrale croisée

La fonction spectrum() peut aussi être utilisée sur un objet mts renfermant deux séries mesurées aux mêmes dates. Dans ce cas, le calcul renvoie un objet spec plus complet dont la méthode plot() permet de tracer trois graphiques différents. Le premier (par défaut) est le périodogramme superposé des deux séries. Le second est obtenu en indiquant l’argument plot.type = "coherency" est le graphe de cohérence au carré qui indique quelles sont les fréquences simultanément significatives dans les deux séries. Enfin, le graphe des phases est obtenu avec l’argument plot.type = "phase". Il montre le déphasage éventuel entre les deux séries à chaque fréquence. Tous ces graphes sont accompagnés d’une indication de l’intervalle de confiance à 95%. Pour bien comprendre ces graphiques, reprenons notre série artificielle à laquelle nous avons ajouté la même série décalée dans le temps de 5 mois mtser.

mtser_spc <- spectrum(mtser, spans = c(3, 3))

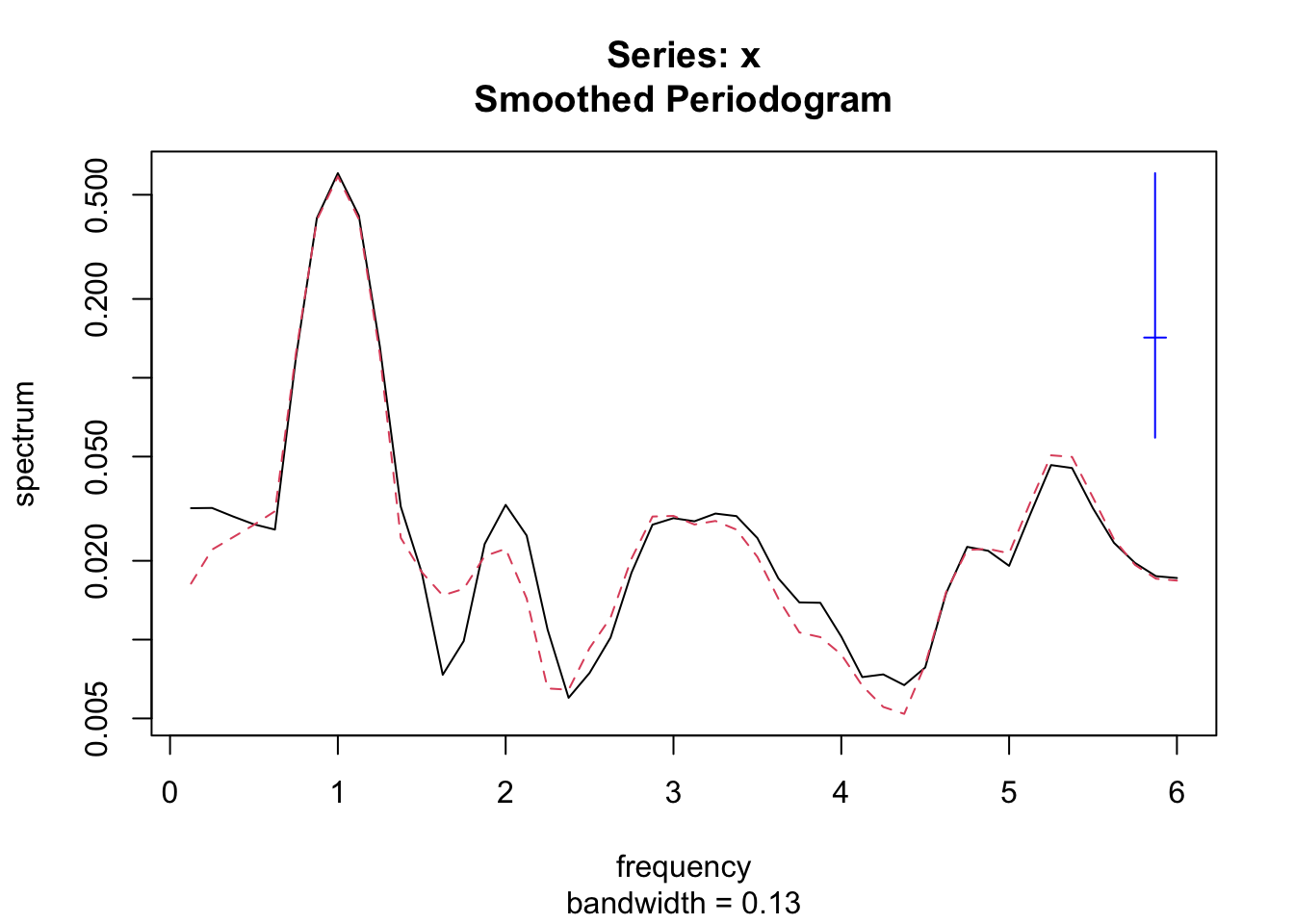
Le périodogramme dans ce premier graphique (obtenu par défaut à partir de spectrum()) nous indique que seule la fréquence un est significative, et ce, dans les deux séries (trait noir plein et rouge pointillé).

plot(mtser_spc, plot.type = "coherency")

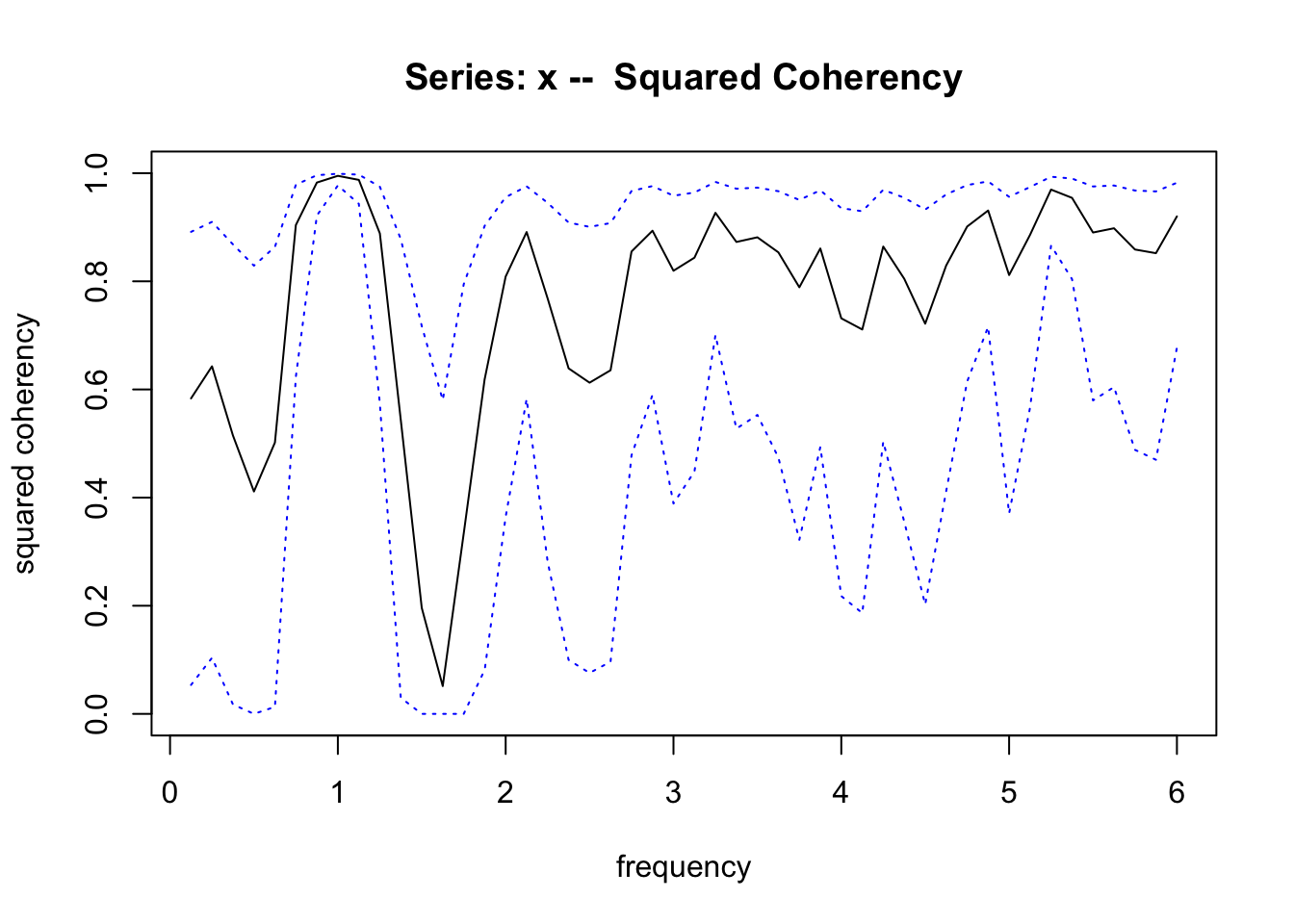
Le graphique de la cohérence au carré nous montre aussi que les deux séries ont une cohérence maximale et très nette pour une fréquence de 1 (l’enveloppe de confiance à 95% en bleu se resserre très nettement à cet endroit). Avec des données artificielles aussi nettes, les deux graphiques peuvent sembler redondants. En pratique, le graphique de cohérence au carré est plus efficace pour détecter la cohérence cyclique entre les deux séries que les périodogrammes superposés.

plot(mtser_spc, plot.type = "phase")

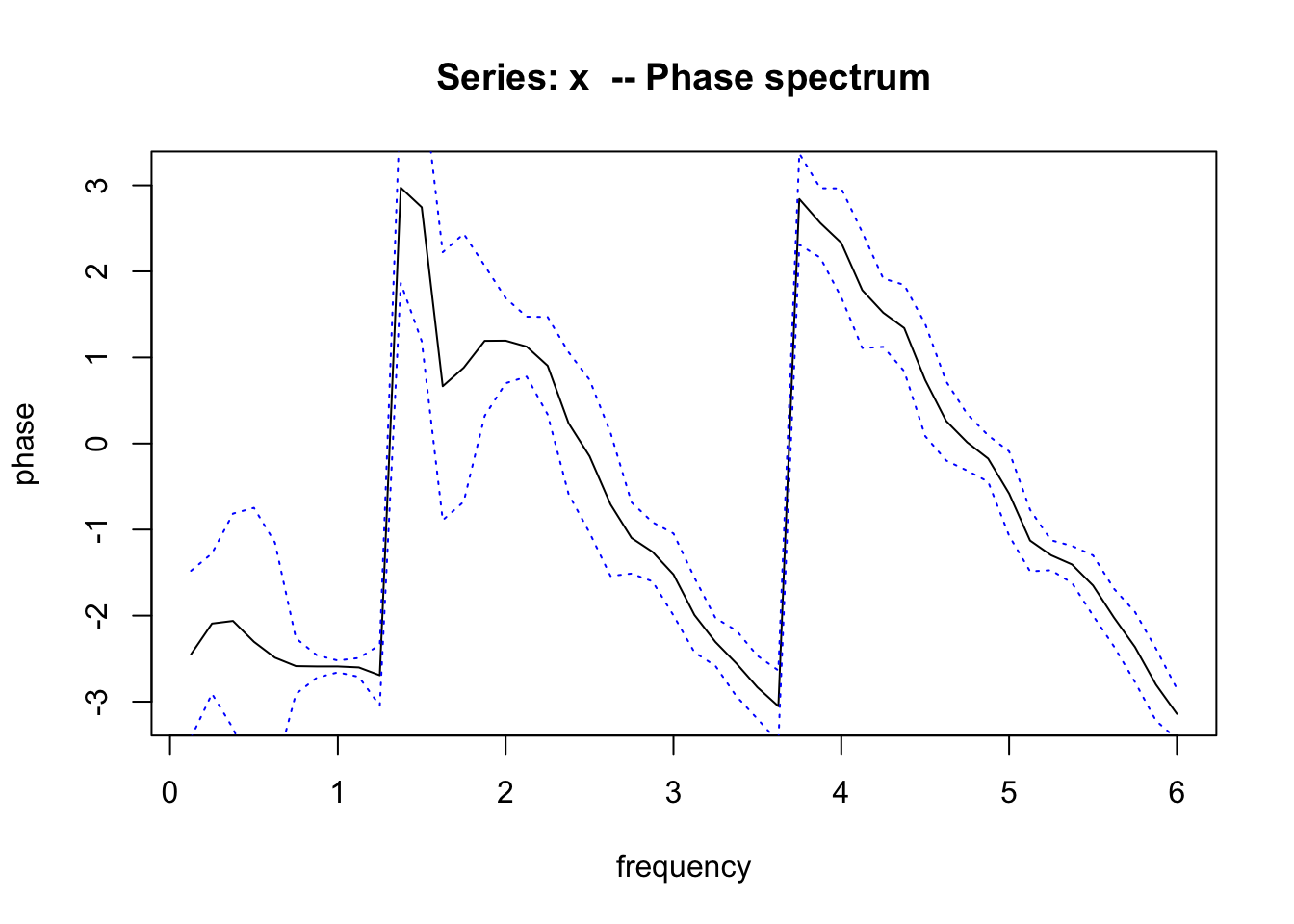
Enfin, le graphique des phases est à lire au niveau de la ou des fréquences significatives et cohérentes. Ici, au niveau de la fréquence de 1. Nous avons un angle de déphasage de -2.6 exprimé en radians (valeur allant de \(-\pi\) à +\(+\pi\)). Un petit calcul est nécessaire pour déterminer le décalage temporel auquel cela correspond. Nous devons diviser la phase par \(2 \pi \omega\) pour obtenir le décalage en unité de mesure temporelle. Comme ici, il s’agit d’une fraction d’année, nous préférons changer d’unité de temps en l’exprimant en mois (multiplication par douze) :

-2.6 / (2 * pi * 1) * 12

# [1] -4.965634

Ceci nous indique que la première série est avancée sur la seconde de 5 mois via une valeur négative. C’est bien exact !

Pour en savoir plus

• Manuel en ligne de {pastecs}, en français. La section consacrée à l’analyse harmonique et spectrale (croisée) est suivie d’explications concernant les points de retournement et de leur application via le tournogramme pour identifier le pas de temps qui maximise l’information dans la série, ainsi que le variogramme et le distogramme qui fournissent des outils complémentaires potentiellement utiles.

• Explication du périodogramme, en anglais.

• Une autre présentation de l’analyse spectrale, théorie et application dans R, en anglais.

4.4.3 Tendance générale

La tendance générale (general trend, en anglais) représente une variation lente dans un sens déterminé. Cependant, si le plus souvent la tendance correspond à une fonction plus ou moins monotone croissante ou décroissante, dans d’autres cas la tendance générale est figurée par le cycle annuel par exemple. Dans ce cas, on parle de tendance cyclique et nous l’analysons via l’analyse spectrale.

Selon l’objet de l’étude entreprise, il peut être tout à la fois aussi important de l’estimer que de l’éliminer. L’estimer, car elle représente la trace la plus évidente et interprétable de l’évolution dans le temps. L’ôter (c’est-à-dire, stationnariser la série), car la part de variance qui lui est attachée est souvent si forte qu’elle peut masquer les autres composantes du signal : cycle long, saison, phénomène de haute fréquence. Les méthodes qui servent à l’estimer ou à l’éliminer font partie des techniques de décomposition des séries spatio-temporelles qui seront étudiées dans le module suivant. Ici, nous nous contenterons de tester son existence.

Il est possible de tester de manière non paramétrique l’existence d’une tendance. Si nous calculons une corrélation linéaire entre les valeurs successives d’un processus et les dates d’observations (définies par une suite d’entiers croissants), on va pouvoir tester si la tendance générale est significativement linéaire, croissante ou décroissante. Cependant, la tendance générale peut être présente et ne pas correspondre à une droite. C’est pourquoi, pour tester l’existence d’une tendance de forme quelconque, on va remplacer les valeurs observées par leurs rangs, puis calculer leur corrélation non paramétrique de Spearman \(\rho\) avec le temps.

Les valeurs du coefficient de Spearman sont comprises entre -1 et +1. Si la série est purement aléatoire, la valeur de \(\rho\) tend vers zéro et sa variance est égale à 1/(n-1). Un test d’hypothèse existe pour déterminer si un coefficient de corrélation est significativement différent de zéro ou non. Nous pouvons réutiliser ce test, mais dans le cas présent, les hypothèses testées sont : \(H_0:\) pas de tendance générale et \(H_1:\) tendance générale présente.

On constate que lorsque le nombre d’ex æquos (correspondant par exemple à des valeurs nulles pour un phénomène rare dans le temps) est supérieur à 80%, la valeur de ce coefficient est totalement biaisée, et donc, le test d’hypothèse associé n’est pas utilisable.

Exemples

On peut estimer si co2 présente une tendance générale significative au seuil \(\alpha\) de 5% comme ceci avec la fonction trend.test() de {pastecs} :

co2 <- read("co2", package = "datasets")
trend.test(co2)

# Warning in cor.test.default(x, time(x), alternative = "two.sided", method =
# "spearman"): Cannot compute exact p-value with ties

# 
#   Spearman's rank correlation rho
# 
# data:  co2 and time(co2)
# S = 199675, p-value < 2.2e-16
# alternative hypothesis: true rho is not equal to 0
# sample estimates:
#      rho 
# 0.988312

L’avis nous prévient qu’il existe des ex æquos. Vérifier qu’ils ne soient pas trop nombreux et toujours considérer dans ce cas-là que le test est approché (autrement dit, se méfier lorsque la valeur p est proche de \(\alpha\)).

# Nombre total d'observations dans la série
(n <- length(co2))

# [1] 468

# Nombre d'ex æquos
n - length(unique(co2))

# [1] 17

Le nombre d’ex æquos est minime ici, et la valeur p est très petite et bien inférieure à \(\alpha\). Nous en concluons que la tendance est significative au seuil \(\alpha\) de 5%. Par ailleurs, comme \(\rho\) est positif (il vaut 0.988), la tendance est à l’augmentation dans le temps. Mais cela, nous l’avions bien évidemment déjà observé sur le graphique de la série.

plot(co2, xlab = "Temps [années]", ylab = expression(paste(CO[2], " atmosphérique [ppm]")))

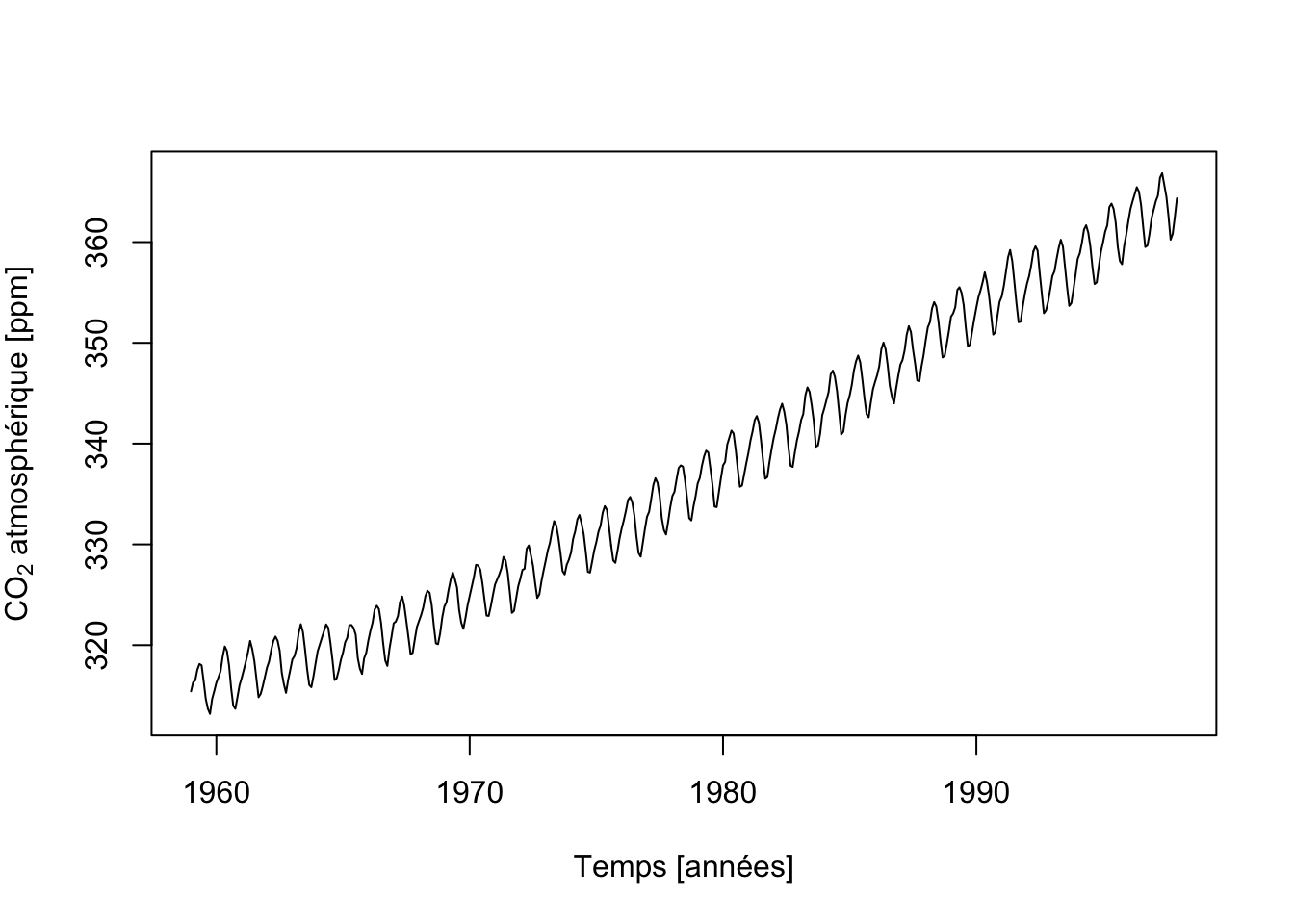
Effectuons le même calcul pour eeg.

eeg <- read("eeg", package = "TSA")
trend.test(eeg)

# Warning in cor.test.default(x[, i], Time, alternative = "two.sided", method =
# "spearman"): Cannot compute exact p-value with ties

# $eeg
# 
#   Spearman's rank correlation rho
# 
# data:  eeg and time(eeg)
# S = 3.6022e+11, p-value = 0.06396
# alternative hypothesis: true rho is not equal to 0
# sample estimates:
#        rho 
# 0.01624775

# Nombre total d'observations dans la série
(n <- length(eeg))

# [1] 13000

# Nombre d'ex æquos
n - length(unique(eeg))

# [1] 11556

Ici, la valeur p est légèrement supérieure à \(\alpha\), mais le nombre d’ex æquos très important ne nous permet pas de tirer de conclusions avec cette forme du test.

4.4.3.1 Test par bootstrap

Les plus futés d’entre vous l’auront remarqué : le test de corrélation exige, en principe, que les observations soient indépendantes les unes des autres. Or, nous nous trouvons ici en présence d’une série chronologique où, par définition, ce n’est pas le cas ! Des corrections sont appliquées en réalité (voir la formule de calcul du test dans le manuel de {pastecs}), mais ce n’est pas toujours suffisant.

Une meilleure version de ce test est réalisée par bootstrap. Cette technique consiste à rééchantillonner aléatoirement l’échantillon pour simuler un grand nombre de fois des mesures différentes de la série. Ce rééchantillonnage introduit une fluctuation dans le calcul de \(\rho\), et il est possible de démontrer que, lorsque n est suffisamment grand et le bootstrap est réalisé correctement, toutes les valeurs obtenues pour le \(\rho\) bootstrapé permettent d’estimer sa distribution réelle. Cette dernière est bien plus proche de la réalité si le bootstrap est réalisé en tenant compte de l’autocorrélation éventuelle de la série. R permet de faire ce type de calcul qui est intégré dans la fonction trend.test() de {pastecs}, en précisant l’argument R = qui indique le nombre de fois que le bootstrap doit être réalisé. Des exemples pratiques sont plus parlants.

Exemples

Testons la tendance dans co2 en bootstrappant 999 fois notre série (on a donc 1000 valeurs de \(\rho\) avec la valeur observée dans l’échantillon de départ.)

set.seed(9037)
(co2_trend_test <- trend.test(co2, R = 999))

# 
# BLOCK BOOTSTRAP FOR TIME SERIES
# 
# Fixed Block Length of 1 
# 
# Call:
# tsboot(tseries = x, statistic = test.trend, R = R, l = 1, sim = "fixed")
# 
# 
# Bootstrap Statistics :
#     original     bias    std. error
# t1* 0.988312 -0.9871328  0.04745857

Le calcul est plus long, mais nous n’avons plus l’avis concernant les ex æquos, car ceux-ci sont pris en compte dans la distribution bootstrappée. Nous voyons que la fonction tsboot() est utilisée en interne. C’est cette fonction qui prend en compte l’autocorrélation temporelle de la série dans le calcul. Mais comment interpréter ce test ? Nous devons passer par une représentation graphique de la distribution bootstrappée :

plot(co2_trend_test)

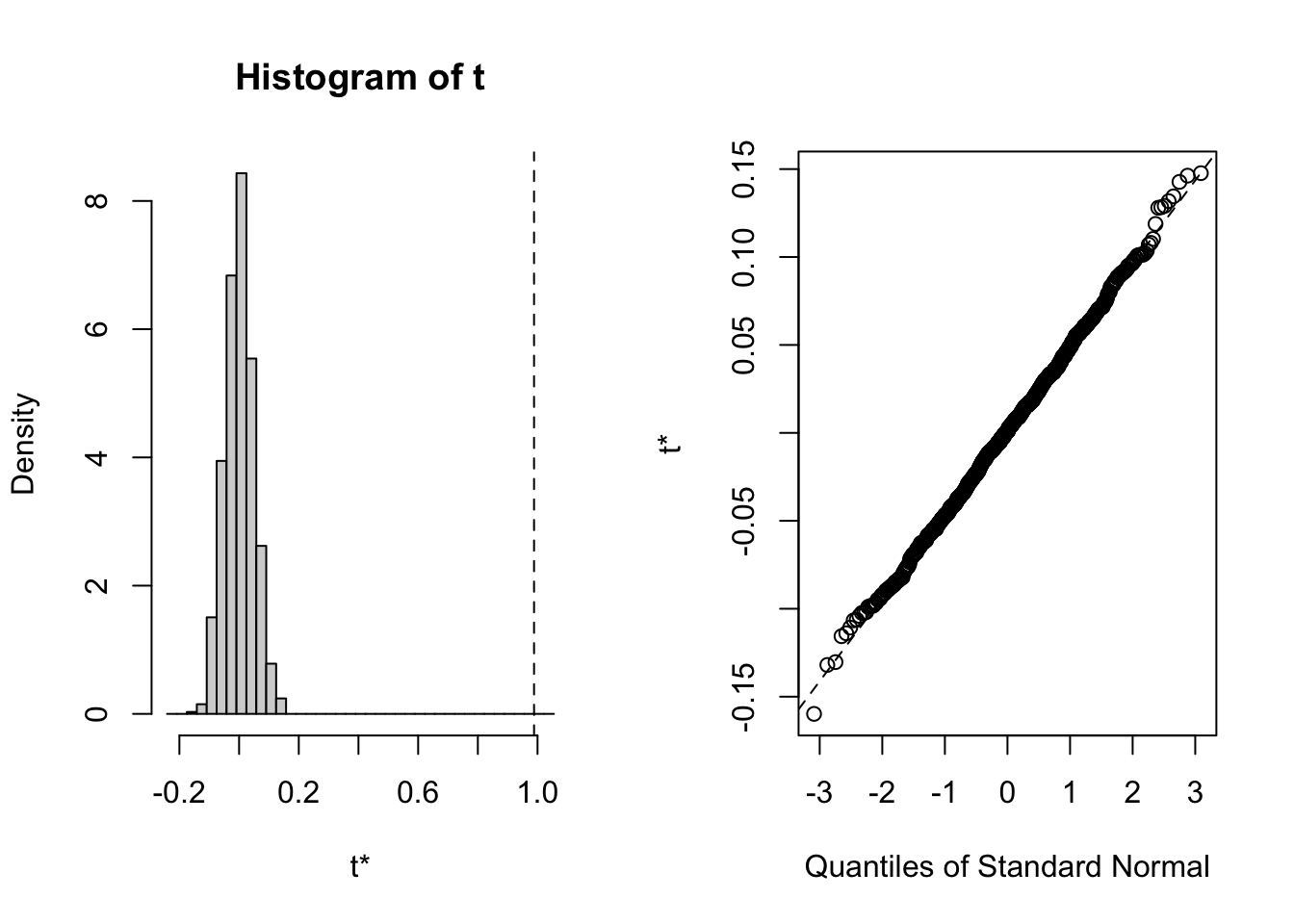
L’histogramme à gauche représente la distribution de \(\rho\), mais après transformation \(t = \rho \cdot \sqrt(\frac{n - 2}{1 - \rho^2})\), nous obtenons en fait une statistique qui suit à peu près une distribution t de Student. Sa valeur bootstrappée est notée \(t^*\). Le trait vertical en pointillé représente la valeur observée dans notre série originale. Nous déterminons combien de fois \(t^*\) est plus extrême (c’est-à-dire, plus grand en valeur absolue) que \(t\) pour un test bilatéral. Ceci représente une estimation de la valeur p du test qui est confrontée à \(\alpha\). Donc, si la valeur p < \(\alpha\), nous rejetons \(H_0\) et concluons qu’une tendance générale significative au seuil \(\alpha\) existe dans la série.

Le graphique de droite vous est familier. Il s’agit d’un graphique quantile-quantile qui compare la distribution \(t^*\) à une distribution théorique t de Student. Nous voyons ici que les deux distributions correspondent bien. Cela signifie que la distribution bootstrappée est quasi confondue à une t de Student. Donc, le test simple non bootstrappé est parfaitement valable dans ce cas-ci (et se calcule bien plus rapidement).

Pour obtenir la valeur p du test, nous faisons :

co2_trend_test$p.value

# [1] 0

De même, nous pouvons obtenir un intervalle de confiance comme ceci :

boot::boot.ci(co2_trend_test, conf = 0.95, type = "norm")

# BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
# Based on 999 bootstrap replicates
# 
# CALL : 
# boot::boot.ci(boot.out = co2_trend_test, conf = 0.95, type = "norm")
# 
# Intervals : 
# Level      Normal        
# 95%   ( 1.8824,  2.0685 )  
# Calculations and Intervals on Original Scale

Comme cet intervalle de confiance ne contient pas zéro, nous en concluons toujours que nous rejetons \(H_0:\). Notez bien que les résultats peuvent varier quelque peu d’un bootstrap à l’autre, et que nous avons utilisé set.seed(x), en prenant bien soin d’utiliser un nombre x différent à chaque fois et pris au hasard, afin de rendre notre analyse reproductible dans ce cours en ligne.

Maintenant que nous avons compris comment utiliser le test bootstrappé sur un exemple où la tendance générale est flagrante, voyons sur un jeu de données plus problématique : eeg. Vu la longueur de la série, nous nous limitons à R = 99, mais plus le nombre de valeurs calculées est grand, plus le résultat est précis naturellement.

set.seed(1563)
(eeg_trend_test <- trend.test(eeg, R = 99))

# 
# BLOCK BOOTSTRAP FOR TIME SERIES
# 
# Fixed Block Length of 1 
# 
# Call:
# tsboot(tseries = x, statistic = test.trend, R = R, l = 1, sim = "fixed")
# 
# 
# Bootstrap Statistics :
#       original      bias    std. error
# t1* 0.01624775 -0.01604486 0.008620437

La valeur de p vaut :

eeg_trend_test$p.value

# [1] 0.06060606

… et le graphique :

plot(eeg_trend_test)

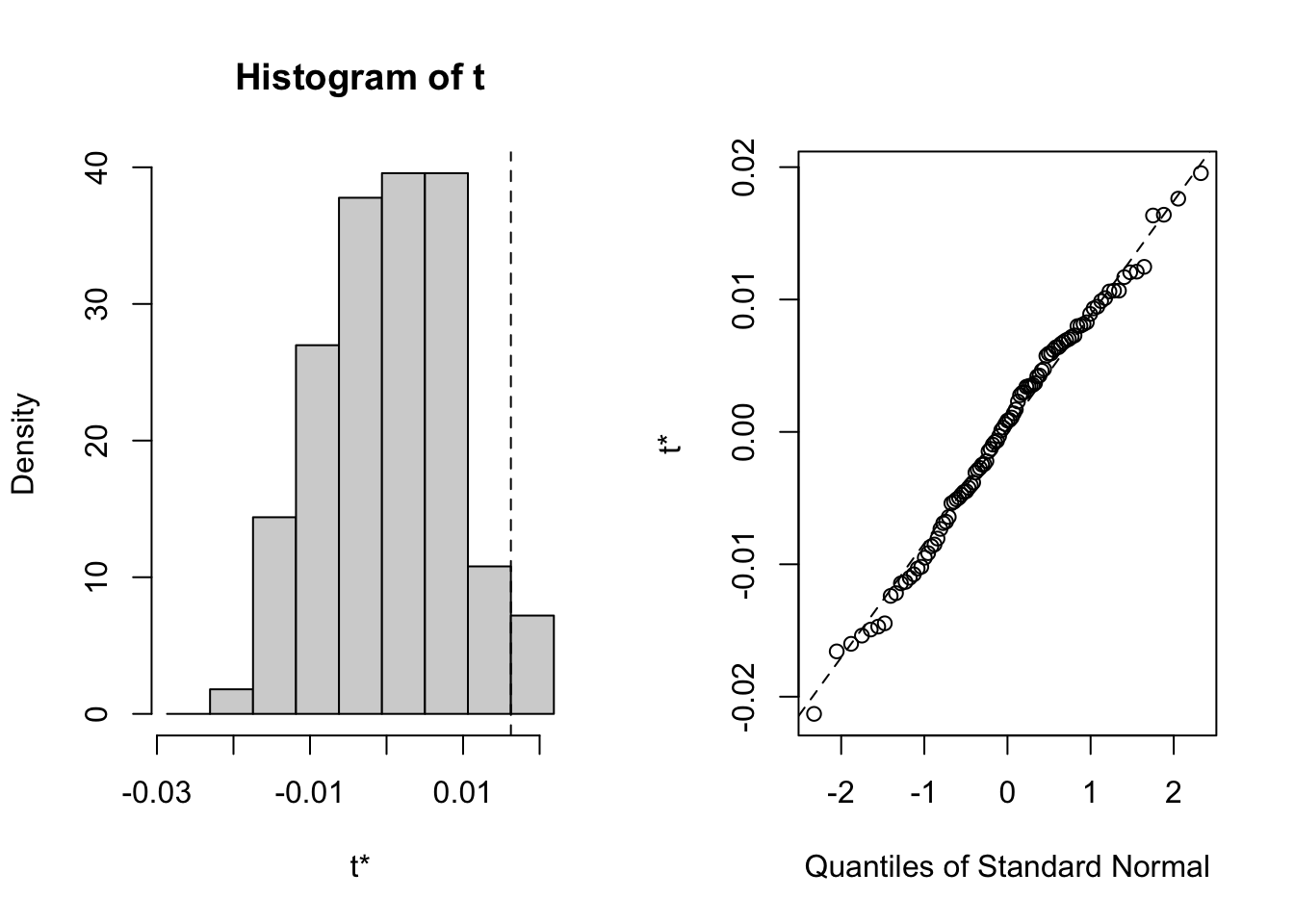
La distribution n’est pas très différente d’une t de Student, et d’autre part, la valeur p vaut 6%, donc juste supérieure à un seuil \(\alpha\) de 5% que nous avons choisi avant de faire ce test. Nous en concluons que nous ne rejetons pas \(H_0\) et que cette série ne comporte pas de tendance générale significative à ce seuil. Dans le cas présent, la valeur p bootstrappée n’est pas très différente de celle calculée à l’aide d’un test paramétrique considérant une distribution théorique idéale. Ceci se produit lorsque les deux distributions (bootstrappée versus théorique) sont similaires, ce que le graphique quantile-quantile de droite nous confirme.

Pour en savoir plus

• Le Manuel en ligne de {pastecs}, en français, détaille les calculs réalisés pour ce test de tendance.

• Une introduction au bootstrap en français et pas trop technique.

• Aide en ligne de la fonction tsboot() qui explique comment le bootstrap sur série chronologique est réalisé, en anglais.

4.4.4 Tendance locale

Nous pouvons être confrontés à des séries qui montrent différentes phases d’évolution à long terme, par exemple, une croissance, suivie d’une décroissance. Dans ce cas, la tendance générale risque de ne pas être significative, alors qu’elle le serait si les deux phases de la série sont séparées l’une de l’autre et analysées individuellement. Ceci montre qu’il est utile d’identifier les cas où des phases successives existent dans notre série, et surtout, à indiquer à quelles date(s) la ou les transitions se font.

Une méthode simple, dite des sommes cumulées, permet de reconnaitre de tels changements de tendance d’une série. Elle permet :

• de détecter les changements survenant dans le niveau moyen de la série,
• de déterminer la date d’apparition de ces changements,
• d’estimer la valeur moyenne d’intervalles homogènes.

En partant d’une série régulière \(x_t\) avec n observations, nous allons choisir une valeur de référence \(k\). Cette valeur est par défaut la moyenne des \(x_t\) pour toute la série, mais nous pouvons très bien choisir une autre constante. Ensuite, nous allons cumuler les observations jusqu’à chaque position \(q\), donc pour \(t = q\), tout en soustrayant \(k\) autant de fois qu’il y a d’observations dans notre somme cumulée (\(q\) fois). Le calcul de la somme cumulée \(S_q\) est donc :

\[S_q = \sum_{i = 1}^q x_{t_i} - q \cdot k\]

Cette somme cumulée est très sensible au changement de la valeur moyenne d’une série. Une propriété de ce type de graphique est que toute moyenne locale se déduit immédiatement de la pente du segment de droite pour ces sommes cumulées, additionné de la valeur de référence \(k\).

Exemple

Partons d’un exemple artificiel. Imaginons une série chronologique de 100 observations pour laquelle les 50 premières ont une moyenne de 4 et les 50 suivantes, une moyenne de 5, simulant ainsi un changement brutal de régime entre la 50^èmeet la 51^ème observations. Cette série présente enfin un bruit blanc important qui masque cette transition, et qui rend en tous cas son positionnement précis sur l’axe du temps impossible.

# Tendances locales
trend <- ts(c(rep(4, 50), rep(5, 50)))
# Bruit blanc
set.seed(742)
noise <- ts(rnorm(100, sd = 0.8))
# Série artificielle
ts2 <- trend + noise
plot(ts2)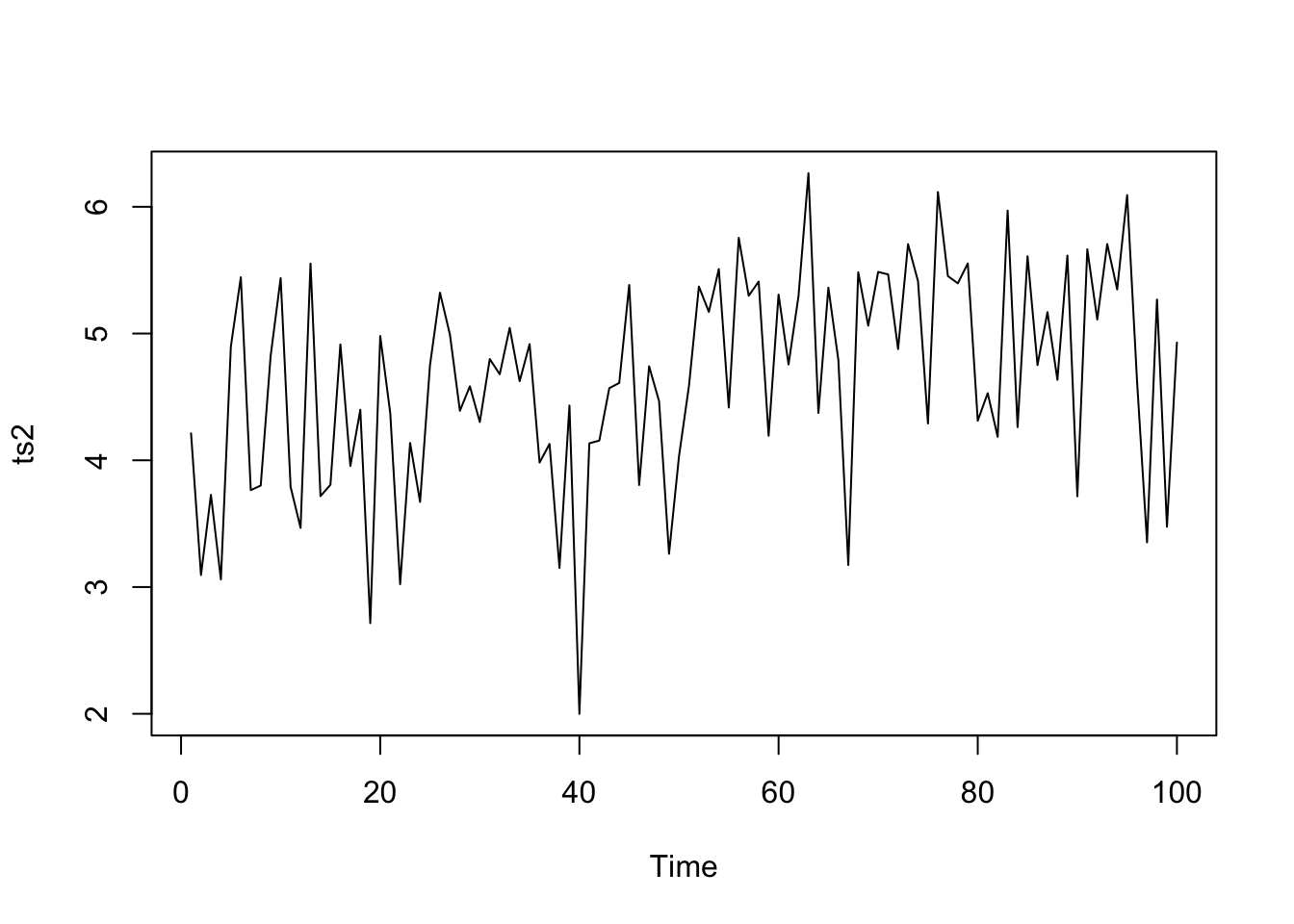

La transition nette entre deux périodes constantes par ailleurs n’est pas visible tant le bruit blanc est dominant et masque cela. Traçons maintenant le graphique des sommes cumulées de cette série à l’aide de local.trend() :

ts2_lt <- local.trend(ts2)

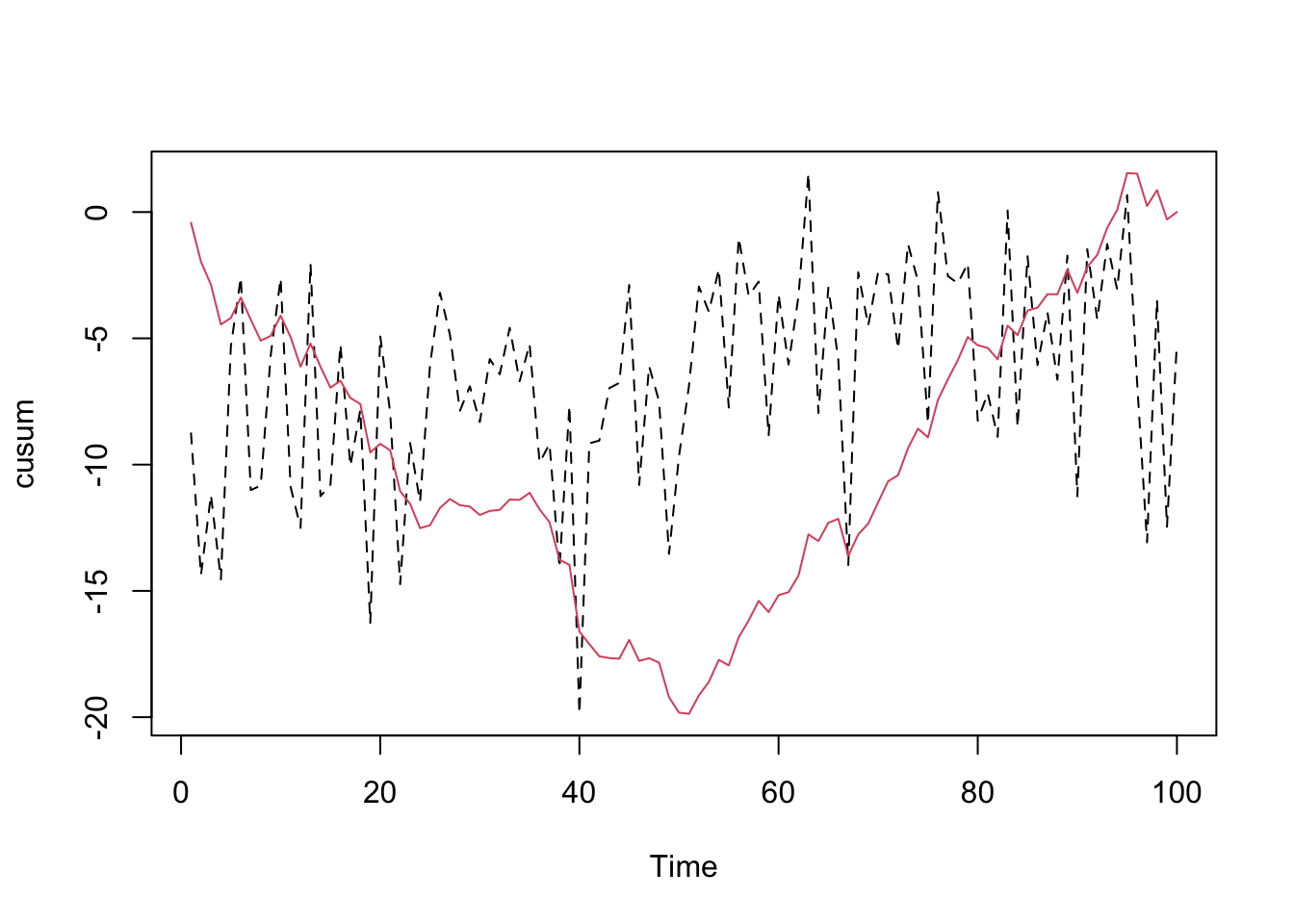
Le graphique montre la série en trait noir pointillé sur laquelle le signal des sommes cumulées est superposé en rouge. Le but pour détecter les phases différentes est de considérer ces sommes cumulées comme un ensemble de segments de droites, et d’identifier les points de départ et de fin de chaque segment. Il ne faut pas regarder trop dans le détail. Ici, les sommes cumulées forment globalement un “V” très net. Elles sont donc composées de deux segments de droites qui représentent les deux branches du “V”.

Lorsque le graphique est tracé dans l’onglet “Plots” de RStudio, il peut être manipulé de manière interactive. La fonction identify() permet alors de cliquer sur des points et d’enregistrer leurs positions sur le graphique. Dans un document R Markdown, cette interaction n’est pas possible malheureusement… et de toute façon, elle n’est pas automatisable, rendant le document Markdown non reproductible.

À ce stade, il est tout de même très pratique de pouvoir cliquer sur le graphique pour identifier les différents segments de droites. Vous pouvez le faire en exécutant le code suivant dans l’onglet “Console” de RStudio en le copiant depuis le document R Markdown (ou du document en ligne) et en le collant dans la console R.

# Copiez et collez ces lignes de code dans la console et exécutez-les
# Données (remplacez par votre propre code)
trend <- ts(c(rep(4, 50), rep(5, 50)))
set.seed(742)
noise <- ts(rnorm(100, sd = 0.8))
ts2 <- trend + noise
# Analyse des tendances locales
ts2_lt <- local.trend(ts2)
identify(ts2_lt)

Ensuite, vous cliquez sur les points du graphique qui vous semblent définir les deux segments de droites formant le “V” (donc, la première observation, puis celle à la pointe du “V”, et enfin, une observation vers la fin de la série). Le gif animé suivant montre cette procédure.

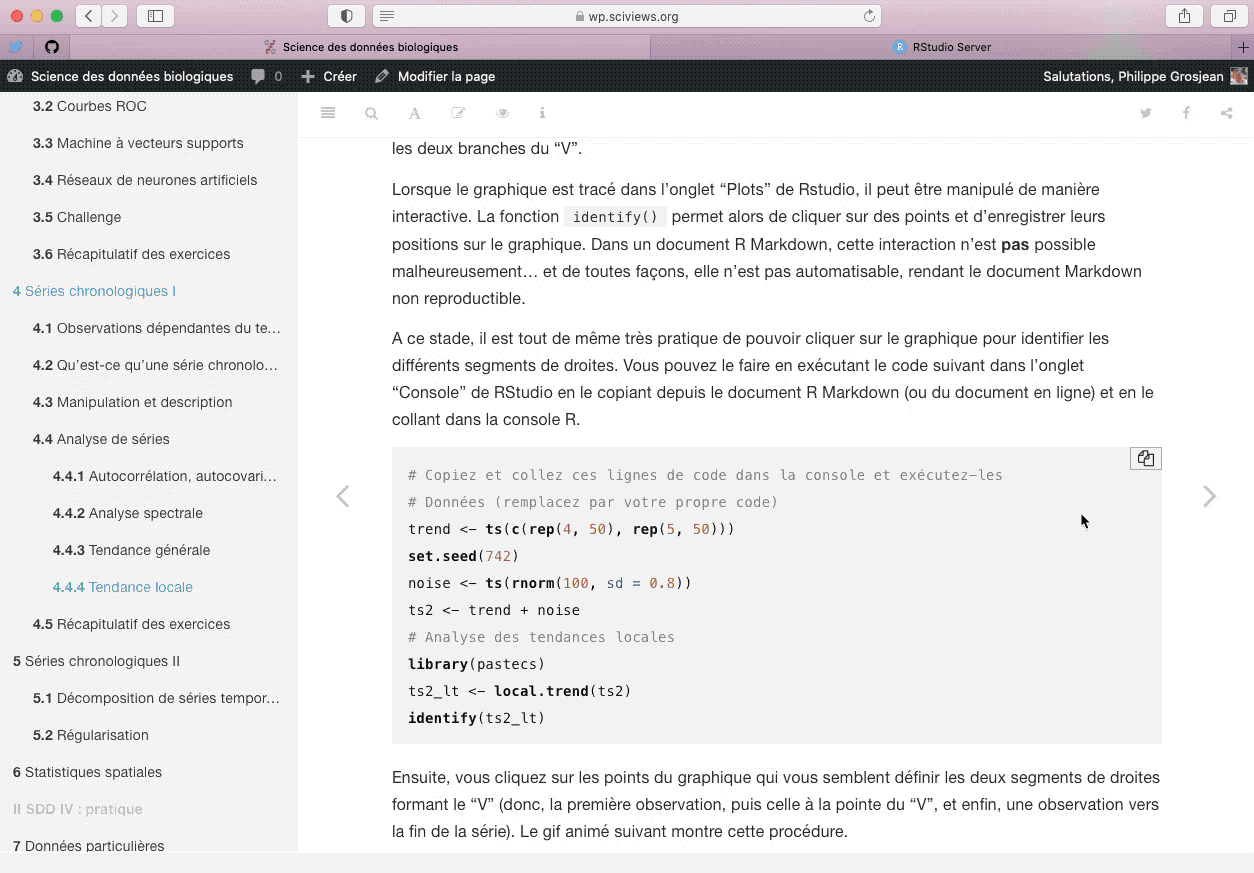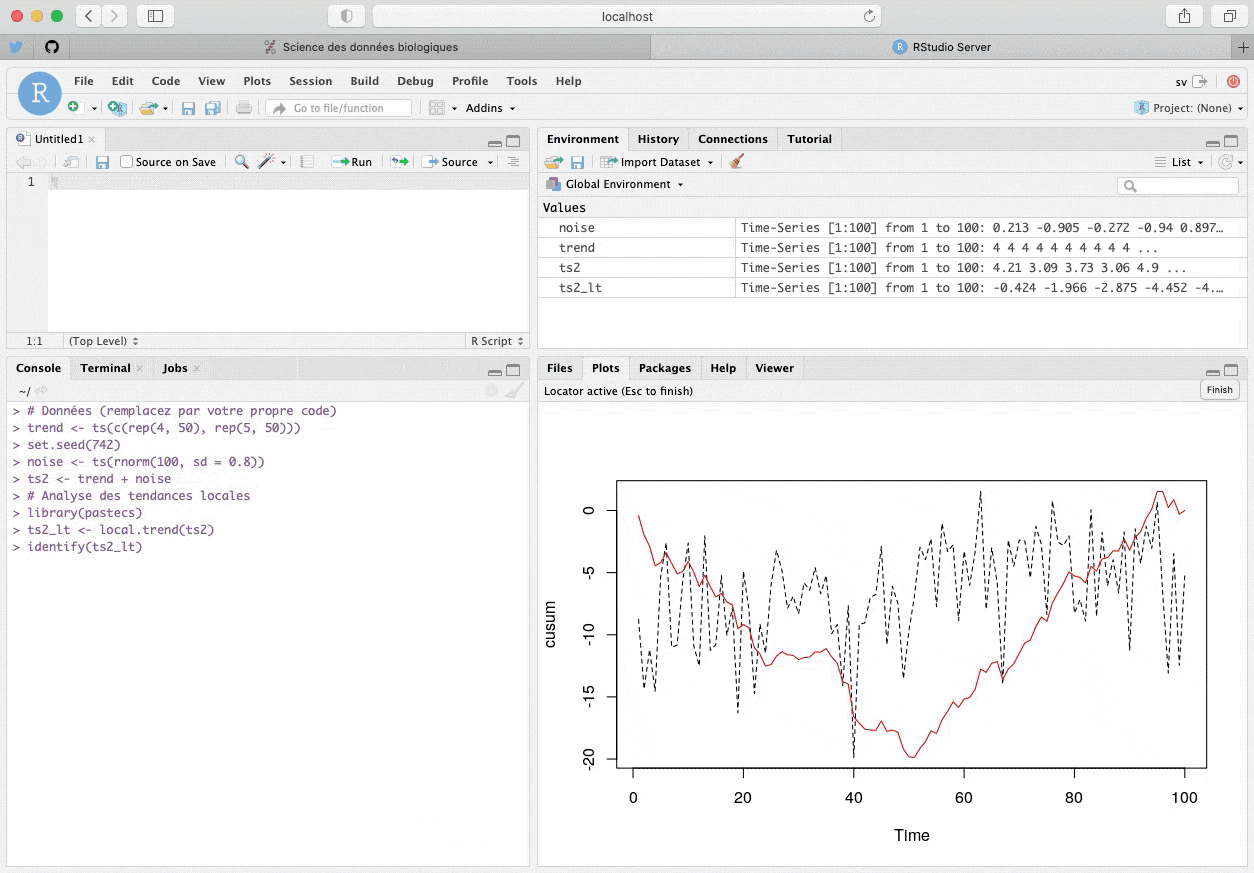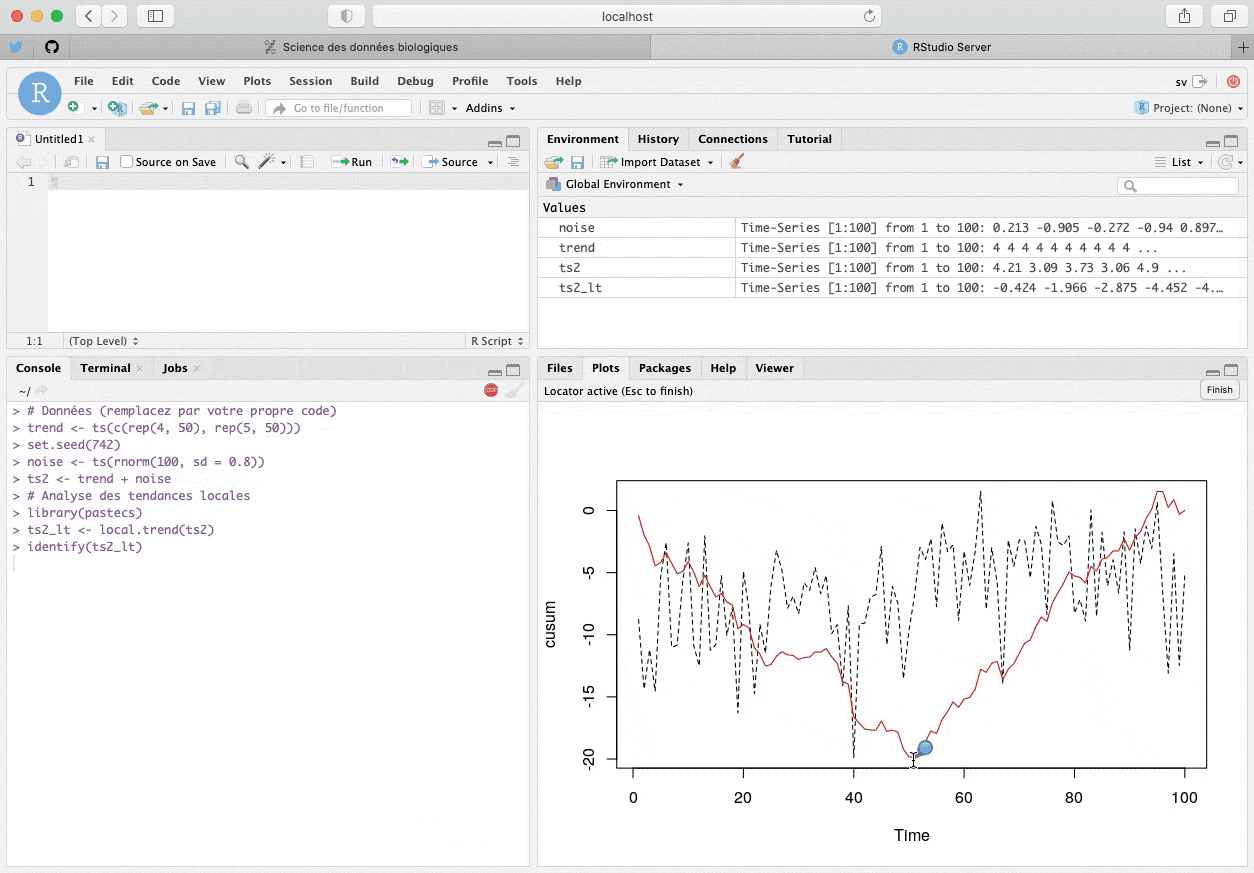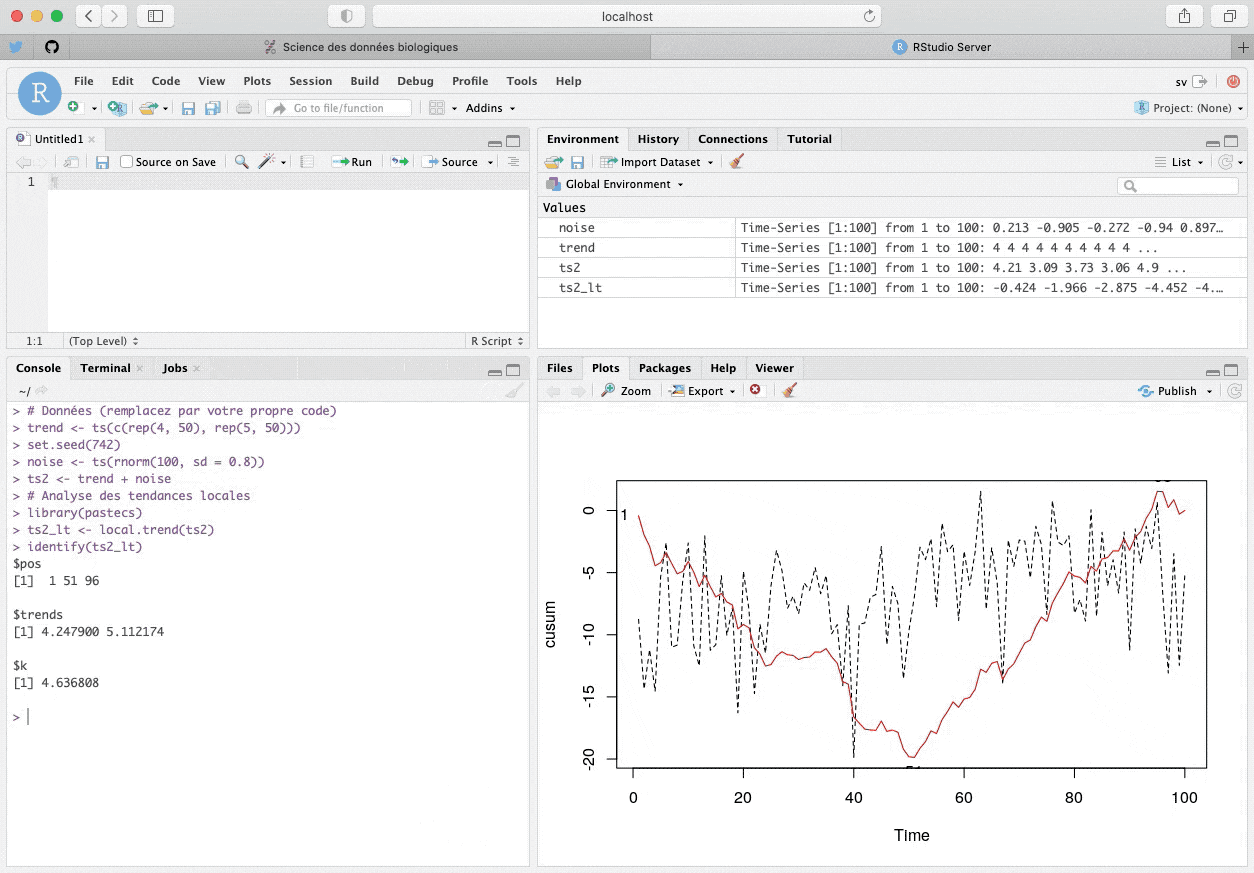
Utilisation de identify() avec un graphique généré à la Console R pour déterminer les points de transitions des segments de droites représentant les sommes cumulées.

Le vecteur $pos renvoie les index des points cliqués dans la série. Les tendances moyennes entre ces points sont renvoyées dans $trends. La valeur de référence \(k\) est ici reportée (par défaut c’est la moyenne de toute la série, ou la valeur de $k indiquée en utilisant local.trend(series, k = …)). Nous avons identifié trois points ($pos) : le 1^er, le 51^èmeet le 96^ème. Nous allons maintenant utiliser le code suivant dans un chunk de notre document R Markdown pour “rejouer” notre analyse et obtenir les résultats dans notre rapport :

# Créer un vecteur ici avec les positions cliquées sur le graphique
pos <- c(1, 51, 96)
# Fonction pour le calcul
lt_calc <- function(x, pos) {
  n <- length(pos)
  k <- attr(x, "k")
  x_val <- as.numeric(x)[pos]
  trends <- (x_val[2:n] - x_val[1:(n - 1)]) / (pos[2:n] - pos[1:(n - 1)]) + k
  list(pos = pos, trends = trends, k = k)
}
# Calcul des tendances locales
lt_calc(ts2_lt, pos)

# $pos
# [1]  1 51 96
# 
# $trends
# [1] 4.247900 5.112174
# 
# $k
# [1] 4.636808

Nous avons identifié deux phases. La première commence à la première observation et se termine à la 51^ème avec une moyenne de 4,24. La seconde commence à la 51^èmeet se termine à la 96^ème avec une moyenne de 5,11. La technique a donc effectué un bon travail pour retrouver les deux phases sur l’axe t, et a donné des estimations pas trop mauvaises des moyennes durant ces deux phases, compte tenu du bruit blanc important dans la série.

Si vous avez affaire à un objet mts, n’oubliez pas d’extraire la série que vous voulez traiter avec local.trend() à l’aide de l’opérateur [,].

À vous de jouer !

Réalisez en groupe le travail C04Ga_ts_cheatsheet, partie I.

Travail en groupe de 4 pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2022-12-09 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie I.

Exercez-vous

Appliquez la technique des sommes cumulées sur les diverses séries d’exemples pour vous familiariser avec son utilisation, en particulier la partie interactive avec identify() dans la console R de RStudio :

• Est-ce que cette technique est appropriée pour co2 ? Pourquoi ?
• L’application sur lynx pose un challenge à cause d’une dominance très nette de cycles.
• Pour eeg, malgré qu’il s’agisse d’une série univariée, elle est encodée comme une matrice. Vous devez donc utiliser eeg[, 1] dans local.trend(). Ici, la technique prend tout son sens.
• De même pour marbioet marphy où nous savons d’emblée qu’il existe différentes phases successives correspondant aux différentes masses d’eaux traversées par le transect.

À vous de jouer !

Réalisez le travail C04Ia_ts.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2022-11-25 12:30:00.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md.