1.3 Outils de diagnostic
Une fois la meilleure droite de régression obtenue, le travail est loin d’être terminé. Il se peut que le nuage de point ne soit pas tout à fait linéaire, que sa dispersion ne soit pas homogène, que les résidus n’aient pas une distribution Normale, qu’il existe des valeurs extrêmes aberrantes, ou qui “tirent la droite vers elle” de manière excessive (points trop influents).
Nous allons maintenant devoir diagnostiquer ces possibles problèmes. L’analyse des résidus permet de le faire. Ensuite, si deux ou plusieurs modèles sont utilisables, il nous faut décider lequel conserver. Enfin, nous pouvons extraire de l’information liée à notre modèle de manière réutilisable dans R ou faire de la prédiction pour de nouvelles observations.
1.3.1 Analyse des résidus
Le tableau numérique obtenu à l’aide de summary() peut faire penser que l’étude d’une régression linéaire se limite à examiner quelques valeurs numériques et divers tests d’hypothèses associés. Ce sont effectivement des indicateurs utiles, mais c’est oublier que la technique est essentiellement visuelle. Le graphique du nuage de points avec la droite superposée est un premier outil diagnostique visuel indispensable, mais il n’est pas le seul ! Plusieurs graphiques spécifiques existent pour mettre en évidence diverses propriétés des résidus qui peuvent révéler des problèmes. Leur inspection est indispensable et s’appelle l’analyse des résidus.
1.3.1.1 Graphique résidus versus valeurs prédites
Avant de se lancer dans l’analyse des résidus, on vérifie le nombre d’observations qui se trouvent dans le set d’apprentissage utilisé. Si ce nombre est trop faible, nous ne pourrons pas faire grand-chose (pour fixer les idées, moins d’une dizaine de points). S’il est moyennement bas, nous n’aurons qu’une analyse approchante (entre une dizaine et une trentaine d’observations). Entre une trentaine et quelques centaines de points, nous sommes dans une zone idéale. Mais si nous avons un très gros jeu de données avec plusieurs milliers de points, alors les graphiques seront très lents à se construire et seront peu lisibles. Avec un très grand nombre d’observations, on peut facilement séparer un set d’apprentissage et un set de test et plutôt travailler sur base du set de test avec des métriques adaptées. Nous ferons cela dans le cours de science des données III. Naturellement, si le jeu de données est très volumineux, on peut aussi commencer par en échantillonner quelques centaines de points au hasard pour le ramener à un tableau plus raisonnable pour les graphiques d’analyse des résidus. Ici, avec 31 observations, on est dans la plage inférieure, mais utilisable.
Le premier des graphiques d’analyse des résidus, que l’on obtient en indiquant un type différent soit par chart(objet_lm, type = "mon_type"), soit en abrégé via chart$mon_type(objet_lm) permet de vérifier visuellement la distribution des résidus (valeurs prédites sur l’axe X et résidus sur l’axe Y). C’est le type resfitted.
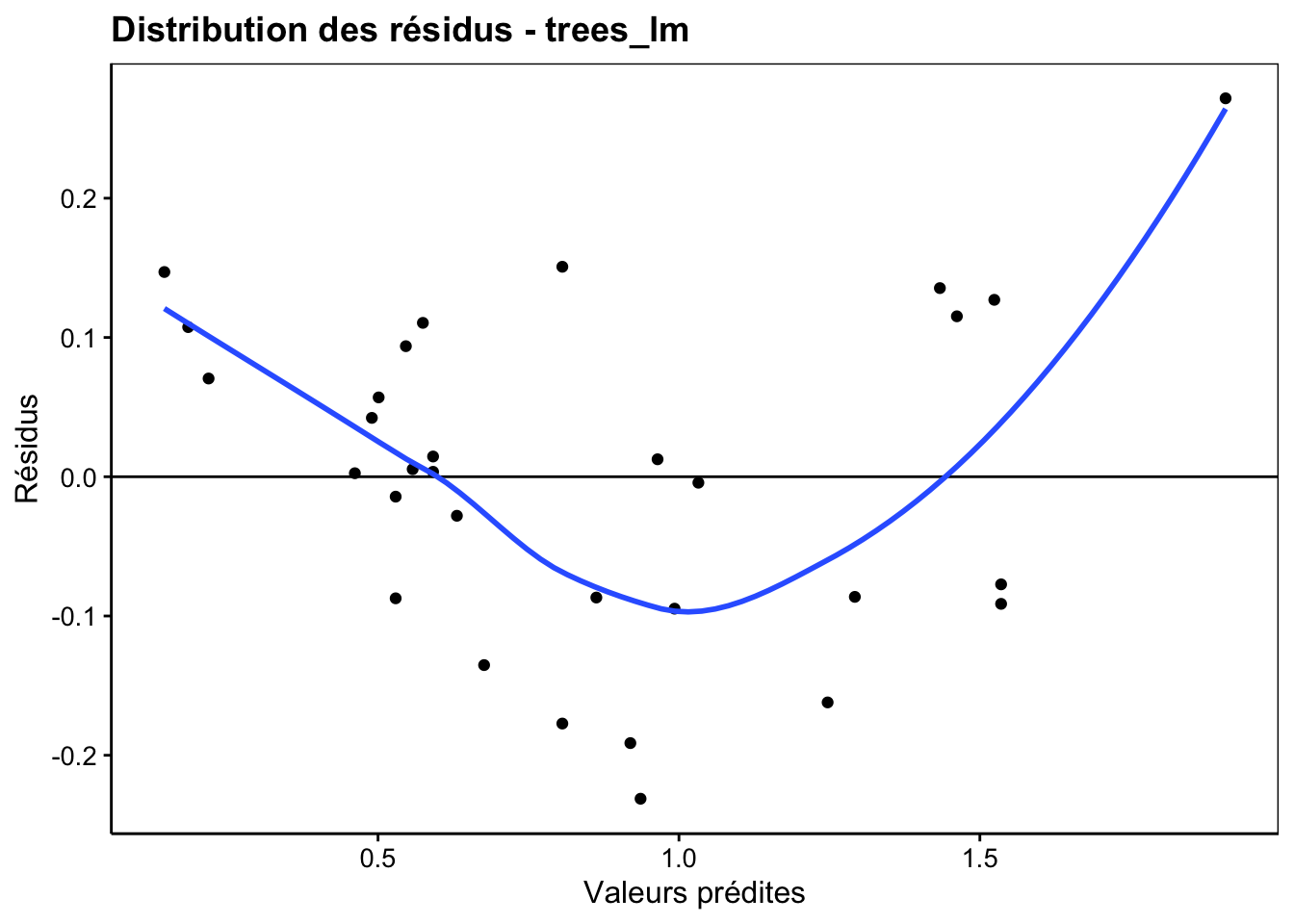
Pour étudier ce graphique, commencez par regarder l’étendue des résidus sur l’axe Y . Comparer-là à l’étendue des valeurs prédites (sur l’axe X). Plus elle sera proportionnellement petite, mieux ce sera : nous avons alors des résidus faibles. Ici, on va de -0.2 à +2.5 sur Y, soit un peu plus de 10% de part et d’autre de l’étendue des valeurs ajustées qui est de 2 unités. Ce n’est pas négligeable, mais en même temps, ce n’est pas mauvais.
Avec une bonne régression, nous aurons une distribution équilibrée de part et d’autre du zéro sur l’axe Y, et ce, tout au long de l’axe X . La courbe de tendance en bleu nous aide à visualiser cela. Ici nous avons clairement une forme en “banane” qui tend à montrer que le nuage de points n’est peut-être pas si linéaire que cela en fin de compte.
1.3.1.2 Graphique quantile-quantile
Le second graphique sert à vérifier la Normalité des résidus (comparaison par graphique quantile-quantile à une distribution Normale). Son type est qqplot.
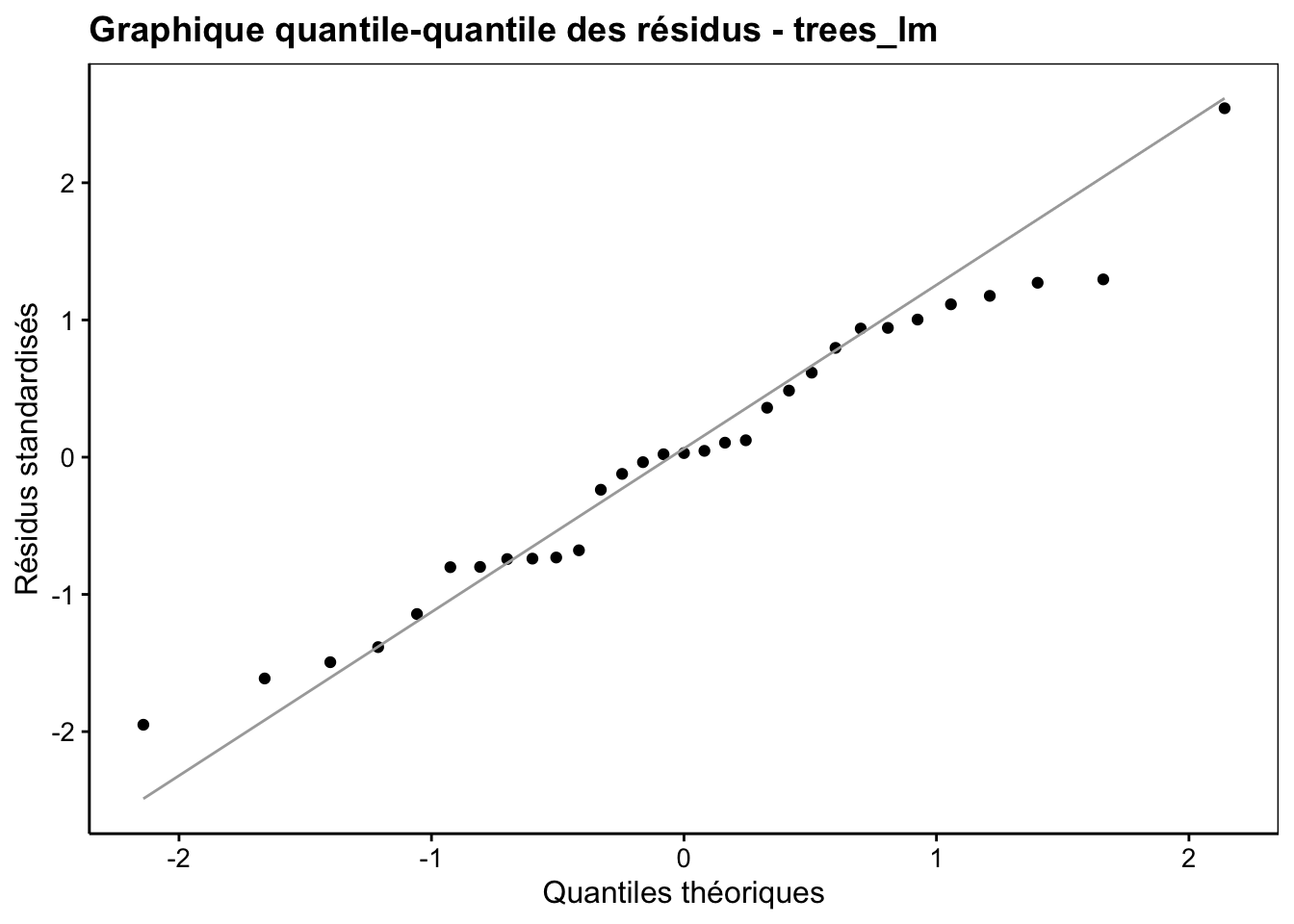
Le graphique quantile-quantile s’interprète en regardant si les points s’alignent plus ou moins bien le long de la droite, en particulier aux extrémités. Des petits écarts sont d’autant plus acceptables que l’échantillon est de petite taille. Ils sont aussi tolérables parce que la régression linéaire est relativement robuste par rapport à ces écarts, surtout si la distribution reste symétrique. Ici nous ne notons pas de difficultés particulières : les points sont assez proches de la droite. Pour être bien clair, le graphique quantile-quantile ne prouve jamais que les résidus suivent effectivement une distribution Normale. Il indique seulement si leur distribution ressemble à la distribution théorique Normale. En fait, dans le cas de notre régression linéaire, ceci est suffisant.
1.3.1.3 Graphique position et échelle
Un troisième graphique (de type scalelocation) va standardiser les résidus, et surtout, en prendre la racine carrée des valeurs absolues pour les présenter sur l’axe Y par rapport aux valeurs ajustées sur l’axe X. Cela a pour effet de superposer les résidus négatifs sur les résidus positifs. Nous y diagnostiquons beaucoup plus facilement des problèmes de dispersion de ces résidus. Ce graphique permet, en effet, de visualiser plus facilement l’étalement des résidus en fonction de valeurs croissantes des valeurs prédites \(\hat y_i\), ce qui revient à en examiner la variance, ou si vous préférez à vérifier s’il y a homoscédasticité (variance constante horizontalement).

Pour l’interprétation, un graphique correct montrera des points qui se distribuent de manière homogène en Y tout au long de l’axe X. La majorité des points semblent confinés dans un tunnel horizontal de hauteur constante. S’il n’y a pas homoscédasticité, la hauteur du tunnel varie de gauche à droite. Ici, le nombre restreint de points ne rend pas le diagnostic facile, mais nous pouvons tout de même nous demander s’il y a homoscédasticité car on a l’impression que la variance des résidus est plus élevée aux deux extrémités.
1.3.1.4 Graphique de la distance de Cook
Le quatrième graphique d’analyse des résidus (type cooksd) met en évidence l’influence des individus sur la régression linéaire, les observations étant rangées dans l’ordre avec le numéro de l’observation qui est la ligne du jeu de données où elle se trouve. Effectivement, la régression linéaire par les moindres carrés est sensible aux valeurs extrêmes dont les résidus déjà importants au départ sont élevés au carré. La distance de Cook mesure l’effet de la suppression du point sur la droite de régression. Plus l’effet est important, plus le point a d’influence.
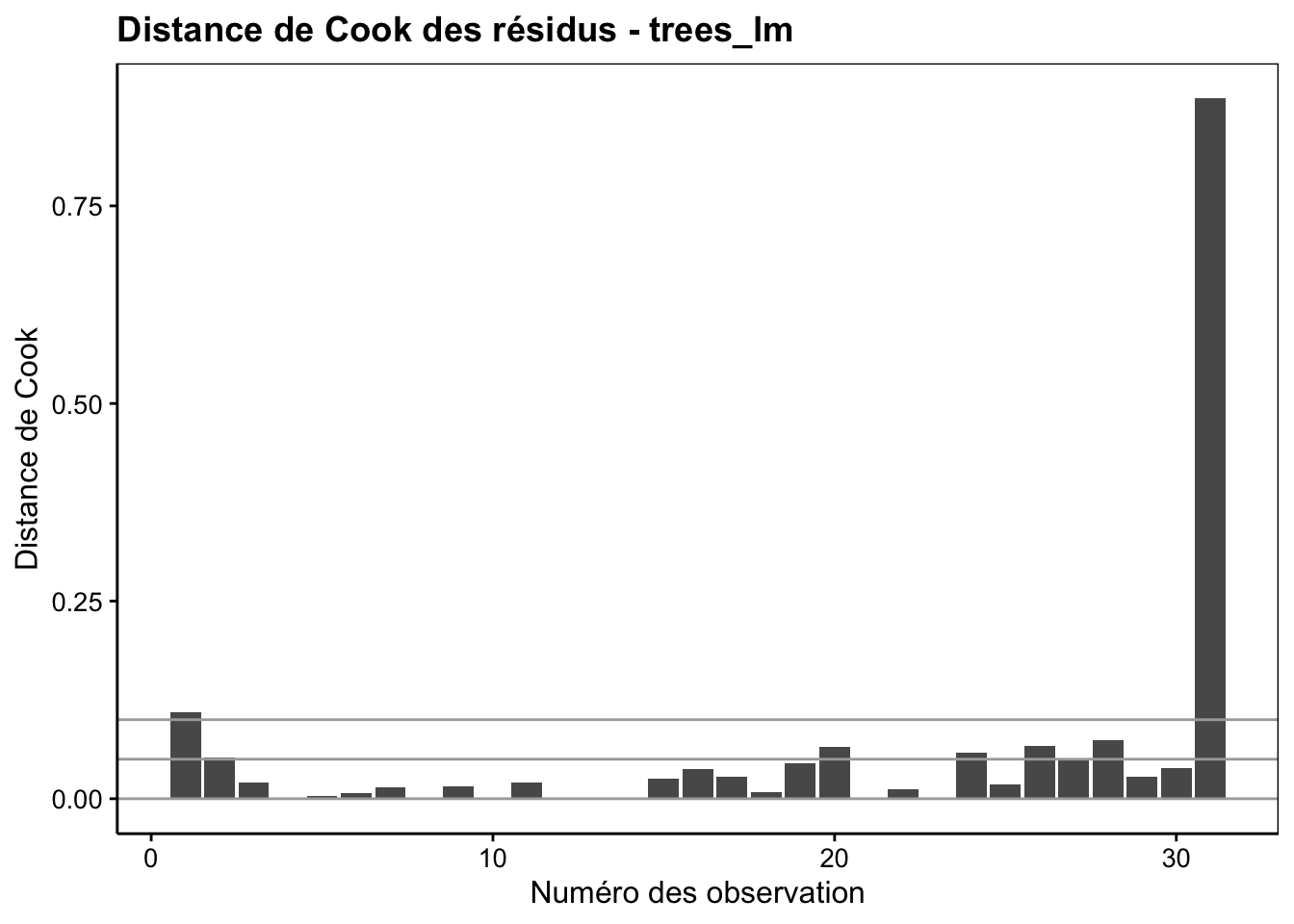
Les points ayant une influence particulièrement forte sont à examiner plus en détail. Ici; il s’agit de la dernière observation du tableau. Deux explications sont possibles. Premièrement, il peut s’agir d’une valeur extrême, aberrante ou non. Deuxièmement, il peut s’agit aussi d’une région dans le plan qui manque d’observations. Un point tout seul à cet endroit, même “normal”, pourra alors avoir une influence importante… Nous allons voir maintenant deux graphiques supplémentaires (complémentaires) pour décrypter ce problème.
1.3.1.5 Graphique de l’effet de levier
Le cinquième graphique utilise l’effet de levier (leverage en anglais, d’où son type resleverage) qui mesure la distance de chaque point à tous les autres le long de l’axe X. Un effet de levier important indique un point isolé à une extrémité. Ce point est donc en position de “tirer” la droite à lui comme un levier. Autant la distance de Cook met en évidence des valeurs extrêmes le long de l’axe Y (variable réponse), autant l’effet de levier le fait le long de l’axe X (variable explicative). Sur le graphique, l’effet de levier est présenté sur l’axe X . Il est complété par deux informations : la valeur standardisée des résidus (écart type ramené à un) sur l’axe Y, et la distance de Cook comme diamètre des points.
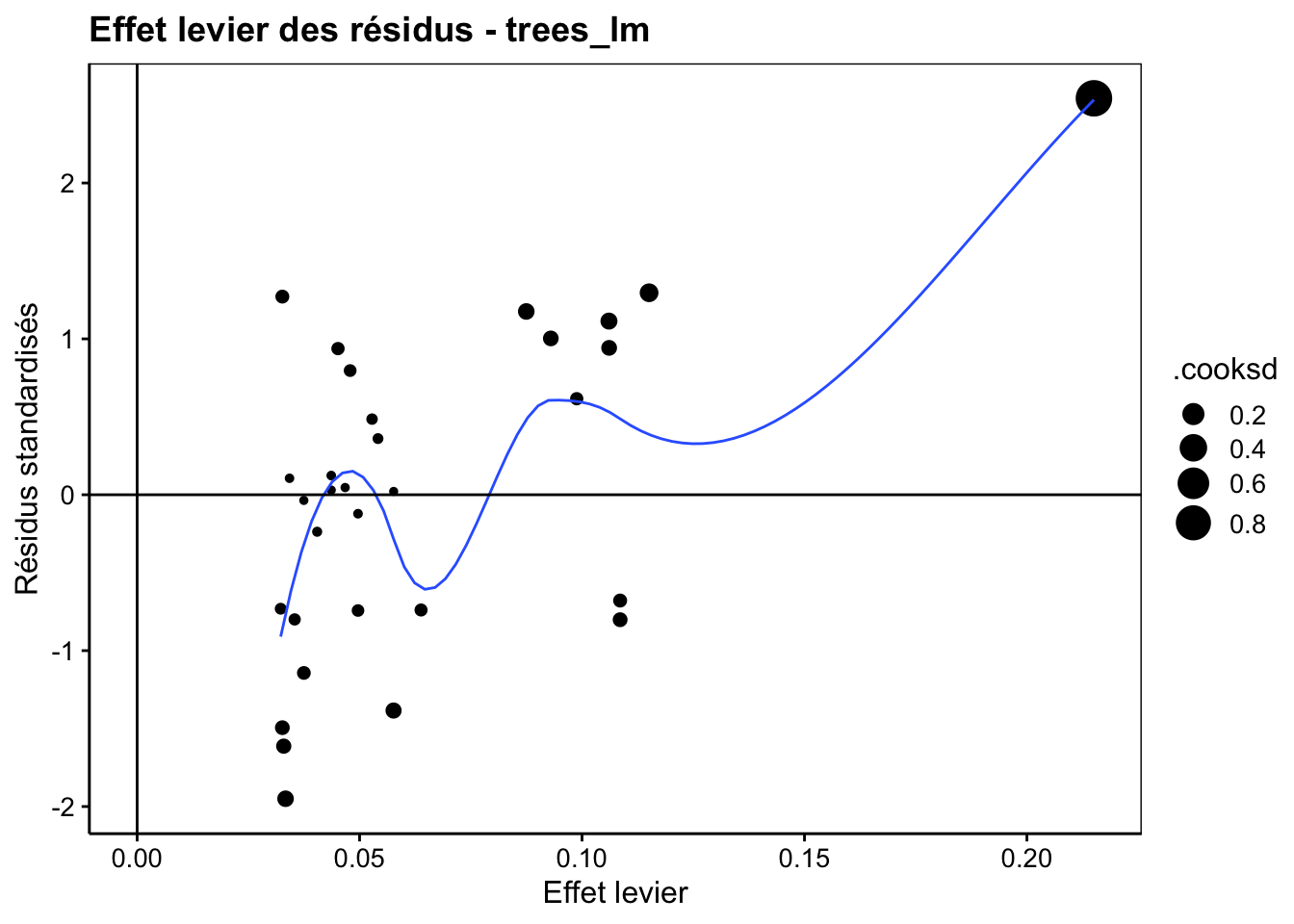
Ici, nous notons que le point qui a la distance de Cook la plus élevée a aussi l’effet de levier le plus fort. Et par la même occasion, c’est le point qui a un résidu le plus grand.
1.3.1.6 Effet de levier versus distance de Cook
Le sixième graphique, de type cookleverage, est une autre variante qui étudie les points extrêmes et influents. Il montre encore l’effet de levier sur l’axe X qu’il oppose cette fois-ci à la distance de Cook sur l’axe Y. L’information sur les résidus (standardisés) n’est pas disponible ici, mais comme dans le graphique précédent, le diamètre des points correspond aussi à la distance de Cook. Souvent, les points influents ressortent encore mieux dans cette représentation.

L’analyse de ce graphique consiste à rechercher un ou plusieurs points influents soit horizontalement (levier), soit verticalement (distance de Cook), soit les deux. Ici nous voyons clairement que le point extrême l’est pour les deux critères simultanément.
Vous noterez que les trois derniers graphiques visent un objectif identique : celui de rechercher des points anormalement influents sur la droite. Il n’est pas utile de les représenter tous les trois. Choisissez celui que vous préférez. Sachant que le second reprend le plus d’information, car il présente les résidus, l’effet de levier et la distance de Cook sur un même graphique, nous conseillons de garder celui-là préférentiellement.
1.3.1.7 Autres graphiques des résidus
Nous avons encore deux autres types que nous ne détaillerons pas ici. Le type reshist représente un histogramme des résidus et le type resautocor étudie l’autocorrélation des résidus par rapport à eux-mêmes, mais décalés d’une observation. Ce dernier graphique est plutôt réservé à des mesures répétées sur le même individu et successives dans le temps, lorsque nous suspectons que la valeur à un temps t peut avoir une influence considérable sur la valeur que l’on observera au temps t + 1 au niveau des résidus. Dans le cours 3, nous étudierons plusieurs techniques relatives à l’analyse de séries chronologiques qui ont cette particularité d’avoir une sorte d’“effet mémoire” au cours du temps.
Ces deux graphiques sont d’un moindre intérêt dans notre exemple. Avec 31 observations, nous sommes un peu court pour observer des effets subtils sur un histogramme. D’autre part, les observations correspondent à des arbres différents et sont donc indépendantes les unes des autres. Nous n’avons pas de raisons de suspecter qu’il puisse y avoir une quelconque autocorrélation.
1.3.1.8 Graphique composite des résidus
Un dernier type, residuals, offre la possibilité de créer directement une figure composée des quatre graphiques les plus utilisés :

Cette composition offre une vision d’ensemble synthétique. Pour une inspection rapide, c’est le meilleur candidat. À l’issue de l’analyse des résidus de trees_lm, nous observons donc différents problèmes qui suggèrent que le modèle choisi n’est peut-être pas le plus adapté. Nous expliquerons pourquoi plus loin, mais à ce stade si vous avez compris le principe et le type d’anomalies que l’on recherche à l’aide de ces différents graphiques de diagnostic, c’est suffisant. Bien analyser les résidus d’une régression n’est pas une tâche facile et on n’y arrive qu’après avoir observé un certain nombre de situations différentes. Vous vous y exercerez avec les différents exercices qui vous seront proposés en présentiel.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel B01Lb_residuals (Analyse des résidus d’une régression).
BioDataScience2::run("B01Lb_residuals")Pièges et astuces : extrapolation
Notre régression linéaire a été réalisée sur des cerisiers noirs dont le diamètre est compris entre 0.211 et 0.523 mètre. Pensez-vous qu’il soit acceptable de prédire des volumes de bois pour des arbres dont le diamètre est inférieur ou supérieur aux valeurs extrêmes de notre jeu de données d’apprentissage (extrapolation) ?
Utilisons notre régression linéaire afin de prédire huit volumes de bois à partir d’arbres dont le diamètre varie entre 0.1 et 0.7m.
Ajoutons une variable pred qui contient les prédictions en volume de bois d’après notre meilleur modèle linéaire. Pour la prédiction, vous pouvez utiliser la fonction predict() qui renvoie un vecteur de résultats, ou add_predictions() qui rajoute une colonne pred à un jeu de données.
# diameter pred
# 1: 0.1000000 -0.482324424
# 2: 0.1857143 0.002092891
# 3: 0.2714286 0.486510206
# 4: 0.3571429 0.970927522
# 5: 0.4428571 1.455344837
# 6: 0.5285714 1.939762152
# 7: 0.6142857 2.424179468
# 8: 0.7000000 2.908596783Observez-vous un problème particulier sur base du tableau obtenu ? Il est peut-être plus simple de voir le problème sur un graphique en nuage de points. Pour un diamètre de 0.1857143 m de diamètre, le volume de bois est de 0 m3, mis en avant par l’intersection des lignes pointillées bleues.
chart(data = trees, volume ~ diameter) +
geom_hline(yintercept = 0, linetype = "dashed", color = "grey") +
geom_vline(xintercept = new_trees$diameter[2],
linetype = "twodash", color = "blue") +
geom_hline(yintercept = new_trees$pred[2],
linetype = "twodash", color = "blue") +
geom_point() +
geom_abline(aes(intercept = trees_lm$coefficients[1], slope = trees_lm$coefficients[2])) +
geom_point(data = new_trees, f_aes(pred~diameter), color = "red") 
Le volume de bois prédit est même négatif pour des arbres encore plus petits ! Notre modèle est-il alors complètement faux ? Rappelons-nous qu’un modèle est nécessairement une vision simplifiée de la réalité. En particulier, notre modèle a été entraîné avec des données comprises dans un intervalle. Il est alors valable pour effectuer des interpolations à l’intérieur de cet intervalle, mais ne peut pas être utilisé pour effectuer des extrapolations en dehors, comme nous venons de le faire, ou alors avec énormément de précautions (pour un phénomène qui varie dans le temps, une extrapolation dans un futur proche est, par exemple, parfois raisonnable).
trees <- add_predictions(trees, trees_lm)
chart(data = trees, volume ~ diameter) +
geom_point() +
geom_line(f_aes(pred ~ diameter))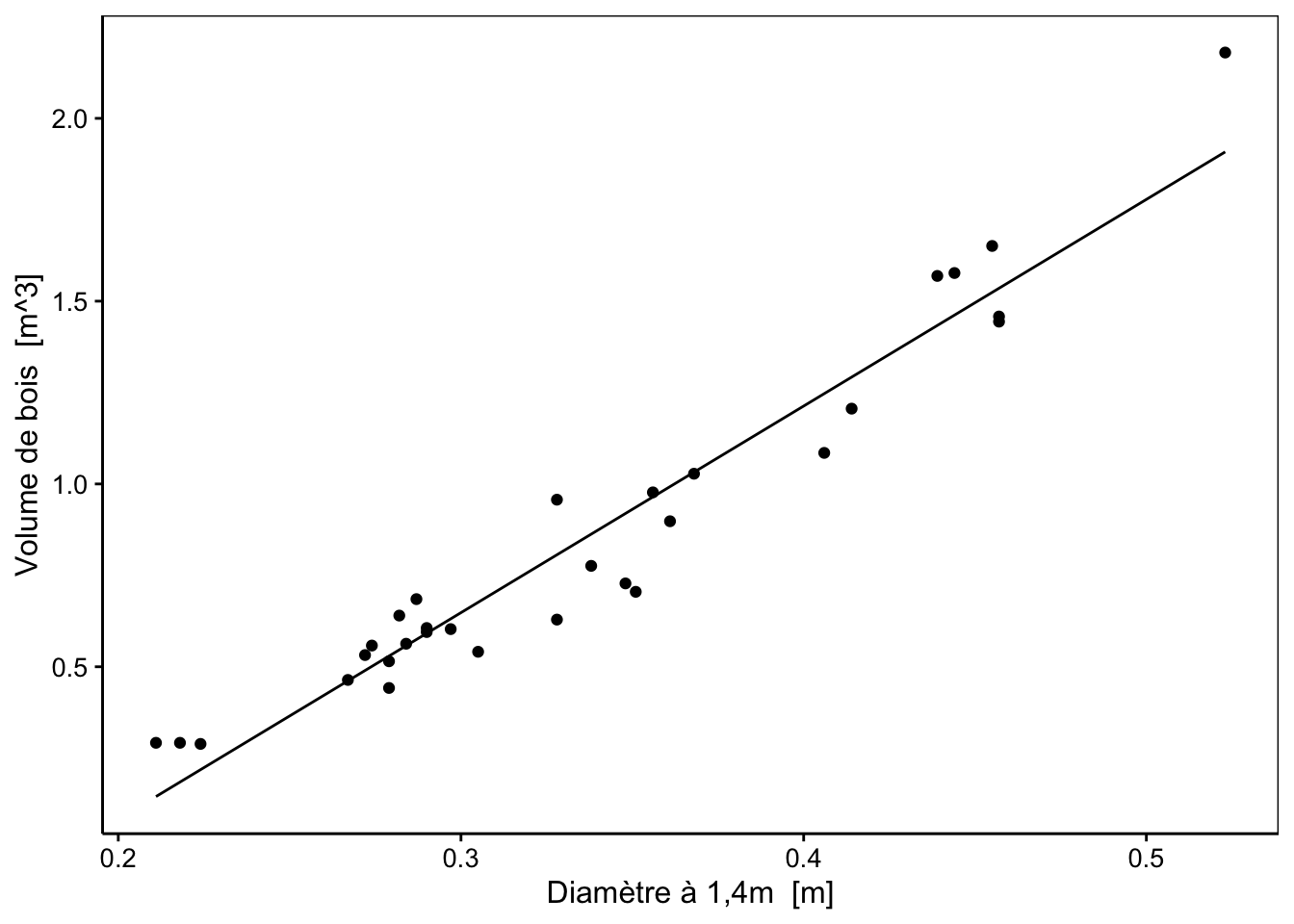
Pièges et astuces : significativité fortuite
Gardez toujours à l’esprit qu’il est possible que votre jeu de données donne une régression significative, mais purement fortuite. Les données supplémentaires de test devraient alors démasquer le problème. D’où l’importance de vérifier/valider votre modèle.
Le principe de parcimonie veut que l’on ne teste pas toutes les combinaisons possibles deux à deux des variables d’un gros jeu de données, mais que l’on restreigne les explorations à des relations qui ont un sens biologique et qui répondent à la question que vous avez posée au départ, afin de minimiser le risque d’obtenir une telle régression de manière fortuite.
À vous de jouer !
Réalisez le travail B01Ia_debug.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q1 : modélisation) à terminer avant le 2023-09-25 12:45:00.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.
1.3.2 Enveloppe de confiance
De même que l’on peut définir un intervalle de confiance dans lequel la moyenne d’un échantillon se situe avec une probabilité donnée, il est aussi possible de calculer et de tracer une enveloppe de confiance qui indique la région dans laquelle le “vrai” modèle se trouve avec une probabilité donnée (généralement, on choisit cette probabilité à 95%). Comme nous l’avons vu plus haut, le graphique chart() par défaut (qui est en fait de type model) le fait pour nous. Voici ce que cela donne en utilisant la fonction stat_smooth() pour ajouter cette enveloppe de confiance sur un graphique que nous composons nous-mêmes :
trees_lm %>.%
(function(lm, model = lm[["model"]], vars = names(model)) {
var_x <- as.symbol(vars[2])
var_y <- as.symbol(vars[1])
chart(data = model, aes(x = !!var_x, y = !!var_y)) +
geom_point() +
stat_smooth(method = "lm", formula = y ~ x)
})(.)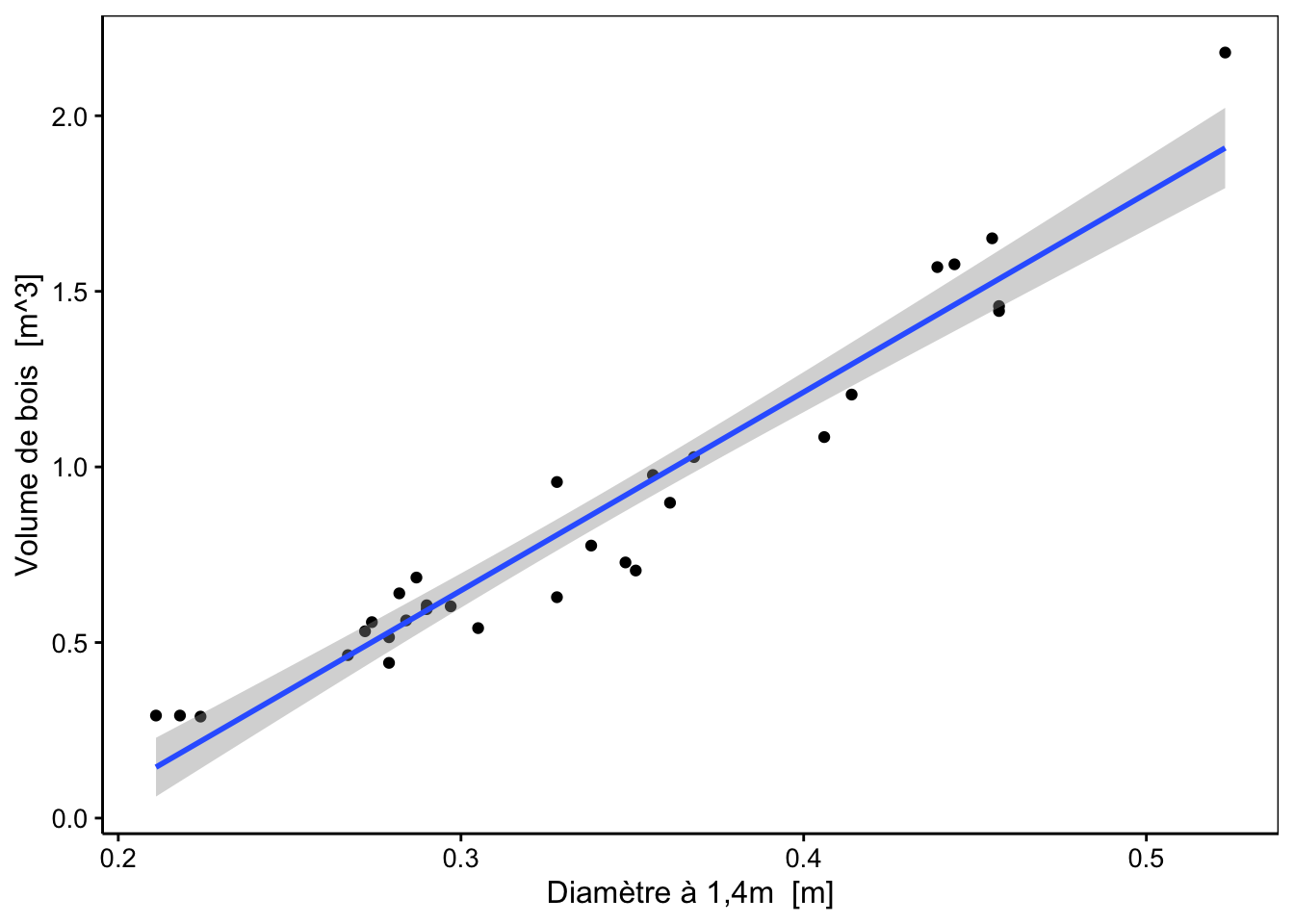
Cette enveloppe de confiance est en réalité basée sur l’écart type conditionnel (écart type de \(y_i\) sachant quelle est la valeur de \(x_i\)) qui se calcule comme suit :
\[s_{y|x}\ =\ \sqrt{ \frac{\sum_{i = 0}^n\left(y_i - \hat y_i\right)^2}{n-2}}\]
À partir de là, il est possible de définir également un intervalle de confiance conditionnel à \(x_i\) :
\[\operatorname{CI}_{1-\alpha}\ =\ \hat y_i\ \ \pm \ t_{\frac{\alpha}{2}}^{n-2} \frac{s_{y|x}\ }{\sqrt{n}}\] C’est cet intervalle de confiance conditionnel qui est matérialisé par l’enveloppe de confiance autour de la droite de régression représentée sur le graphique précédent.
1.3.3 Extraire les données d’un modèle
La fonction tidy() extrait facilement et rapidement sous la forme d’un tableau différentes valeurs associées à la paramétrisation de notre régression linéaire (informations relatives aux paramètres du modèle).
# # A tibble: 2 × 5
# term estimate std.error statistic p.value
# <chr> <dbl> <dbl> <dbl> <dbl>
# 1 (Intercept) -1.05 0.0955 -11.0 7.85e-12
# 2 diameter 5.65 0.276 20.4 9.09e-19On obtient l’équivalent sous forme d’un tableau bien formaté pour un rapport à l’aide de tabularise$tidy()(ici on utilise header = FALSE pour ne pas rajouter d’information supplémentaire au-dessus du tableau comme le type de modèle et son équation) :
Terme | Valeur estimée | Ecart type | Valeur de t | Valeur de p | |
|---|---|---|---|---|---|
Ordonnée à l'origine | -1.05 | 0.0955 | -11.0 | 7.85·10-12 | *** |
Diamètre à 1,4m | 5.65 | 0.2765 | 20.4 | < 2·10-16 | *** |
0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05 | |||||
Pour extraire facilement et rapidement sous la forme d’un tableau des valeurs numériques servant au diagnostic de la qualité d’ajustement d’un modèle, nous pouvons aussi utiliser la fonction glance().
# # A tibble: 1 × 12
# r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
# <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 0.935 0.933 0.121 418. 9.09e-19 1 22.6 -39.2 -34.9
# # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Nous aborderons certaines de ces métriques dans le prochain module. Ici aussi, tabularise$glance() permets d’obtenir un tableau formaté :
R2 | R2 ajusté | RSE | Valeur de t | Valeur de p | Ddl modèle | Log-vraisemblance | AIC | BIC | Déviance | Ddl résidus | N |
|---|---|---|---|---|---|---|---|---|---|---|---|
0.935 | 0.933 | 0.121 | 418 | 9.09·10-19 | 1 | 22.6 | -39.2 | -34.9 | 0.422 | 29 | 31 |
À vous de jouer !
Réalisez le travail B01Ib_abalone.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q1 : modélisation) à terminer avant le 2023-10-02 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.