4.1 Modèle linéaire généralisé

Le modèle linéaire nous a permis de combiner différents types de variables indépendantes ou explicatives dans un même modèle. Cependant, la variable dépendante ou réponse à la gauche de l’équation doit absolument être numérique et une distribution Normale est exigée pour la composante statistique du modèle exprimée dans les résidus \(\epsilon\). Donc, si nous voulons modéliser une variable dépendante qui ne répond pas à ces caractéristiques, nous sommes dans l’impasse avec la fonction lm(). Dans certains cas, une transformation des données peut résoudre le problème. Par exemple, prendre le logarithme d’une variable qui a une distribution log-Normale au départ la normalise. Dans d’autres cas, il semble qu’il n’y ait pas de solution… C’est ici que le modèle linéaire généralisé vient nous sauver la mise.

Le modèle linéaire généralisé se représente comme suit :

\[ g(y) = \alpha + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_l I_1 + \beta_m I_2 + ... + \epsilon \]

La différence par rapport au modèle linéaire, c’est que notre variable dépendante \(y\) est transformée à l’aide d’une fonction \(g(y)\) que l’on appelle fonction de lien. Cette fonction de lien est choisie soigneusement pour transformer une variable qui a une distribution non-Normale vers une distribution Normale ou quasi-Normale. Du coup, il ne faut rien changer dans le membre de droite (à la droite du signe égal) dans l’équation par rapport au modèle linéaire, et les outils existants peuvent être réemployés ou adaptés, une fois la transformation réalisée.

La fonction de lien est utile pour transformer une variable dépendante qui a une distribution non-Normale, mais elle ne résout pas le problème de la distribution des résidus \(\epsilon\) qui serait inadéquate, par exemple, lorsque sa variance n’est pas constante (hétéroscédasticité). Une fonction de variance vient compléter le modèle. Elle décrit comment varie la variance en fonction de la valeur prédite \(\hat{y}\) (forme de base utilisée dans la fonction R glm()) :

\[ \operatorname{var}y = \phi\ V(\hat{y}) \]

avec : - \(V\) la fonction de variance - \(\phi\) (phi) une constante ≥ 0 appelée paramètre de dispersion qui permet de contrôler la variance de la distribution de \(y\). Il est fixé à 1 dans certains cas (voir ci-dessous).

Dans le cas du modèle linéaire, nous aurons l’identité comme fonction de lien \(g(y) = y\) (aucune transformation) et une constante comme fonction de variance \(V(\hat{y}) = 1\) (homoscédasticité) avec \(\phi = /sigma^2\) (concrètement, on utilisera \(s^2\) la variance observée dans l’échantillon comme estimateur \(\hat{\sigma^2}\) de la variance \(\sigma^2\)), ce qui nous mène à la distribution de \(y\) :

\[ g(y) = y \sim \mathcal{N}(\hat{y},\ \phi \ V(\hat{y})) \sim \mathcal{N}(\hat{y},\ \sigma^2) \sim \mathcal{N}(\alpha + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_l I_1 + \beta_m I_2,\ \sigma^2) \] et comme les résidus sont égaux à \(y - \hat{y}\), nous avons :

\[ \epsilon = y - \hat{y} \sim \mathcal{N}(\hat{y},\ \sigma^2) - \hat{y} \sim \mathcal{N}(0,\ \sigma^2) \]

Sans entrer dans les détails, une GLM définie de cette façon ajuste le modèle par maximum de vraisemblance (un concept que nous avions déjà rencontré avec le critère d’Akaiké au module 2, mais sans le détailler). Nous n’irons pas plus loin dans la théorie, mais sachez que le maximum de vraisemblance ajustera le modèle de telle sorte que la distribution observée dans l’échantillon soit la plus proche possible de la distribution définie dans le modèle. Concrètement, dans le cas particulier de la fonction de lien identité et fonction de variance égale à 1, les estimateurs des paramètres \(\alpha\) et \(\beta_i\) seront les mêmes que ceux obtenus avec la fonction lm(). On parlera aussi de déviance des résidus en GLM à la place de la somme des carrés des résidus dans le modèle linéaire classique (notions équivalentes, mais pas exactement identiques, d’où les noms différents).

À vous de jouer !
h5p

Maintenant que nous avons mis en place un modèle général, toute la difficulté tient dans la définition de fonctions de lien et de variance pertinentes par rapport à la distribution de \(y\) et de \(\epsilon\). Le tableau suivant reprend les situations les plus courantes prises en compte par la fonction glm() dans R qui calcule le modèle linéaire généralisé (la fonction de lien par défaut ne doit pas être précisée et la fonction de variance ne doit jamais être indiquée, car elle dépend directement de la famille sauf dans le cas family = quasi(...) non repris ici, voir ?family).

Distribution de y Fonction de lien \(\phi\) Code R
Gaussienne (Normale) identité \(\sigma^2\) glm(..., family = gaussian)
Log-Normale log \(\sigma^2\) glm(..., family = gaussian(link = log))
Poisson log 1 (fixe) glm(..., family = poisson)
Quasi Poisson log \(\sigma^2\) glm(..., family = quasipoisson)
Binomiale logit 1 (fixe) glm(..., family = binomial)
Quasi Binomiale logit \(\sigma^2\) glm(..., family = quasibinomial)

Dans le tableau, “Gaussienne” correspond au modèle linéaire qui est additif alors que “Log-Normale” est un modèle où les termes sont en réalité multiplicatifs9. La distribution de Poisson est utilisée souvent pour des dénombrements ou des abondances (nombres entiers ≥ 0), la distribution binomiale est utilisée pour des proportions ou lorsque la variable est binaire (0 ou 1, oui ou non, présence ou absence, sain ou malade…) La fonction de lien logit est :

\[ logit(\hat{y}) = \log(\frac{\hat{y}}{(1 - \hat{y})} \]

En réalité, nous modélisons ici la transition entre deux états “0” et “1” à l’aide d’une courbe logistique en forme de “S”. Une variation croissante d’une ou plusieurs variables indépendantes \(x_i\) fait passer la proportion des individus du premier état “0” vers le second “1”, selon l’équation suivante :

\[ y = \frac{1}{1 + e^{- \beta_i x_i}} \]

Pensez, par exemple, à des doses croissantes d’un insecticide qui font que la proportion d’insectes morts (état “1”) passe de 0% lorsque la dose est trop faible jusqu’à 100% pour des doses importantes avec une transition progressive pour des doses croissantes.

Les versions “quasi” sont des modèles estimés différemment et qui sont à appliquer lorsqu’il y a surdispersion. Dans le cas des familles binomiale et Poisson, la dispersion \(\phi\) est censée être fixe à 1 en théorie. En pratique, ce n’est pas toujours le cas. Si la variance est bien plus grande, il faudra utiliser les versions “quasi” de ces distributions ou respécifier le modèle (avec préférence pour la seconde, nous verrons un exemple plus loin). Concrètement, nous pourrons avoir une idée de la dispersion observée dans les données en divisant la déviance des résidus par le nombre de degrés de liberté de ces résidus. Si la valeur obtenue est très supérieure 1, nous serons alors dans une situation de surdispersion (overdispersion en anglais). De même, si la valeur est très inférieure à 1, nous serions dans un cas de sousdispersion. Il existe encore d’autres familles de GLM et d’autres fonctions de lien. Voyez l’aide de ?family pour plus de détails.

Pour aller plus loin

La question de la surdispersion des données est encore bien plus complexe que ce qui a été traité ici. Voyez par exemple https://r.qcbs.ca/workshop06/book-fr/que-faire-avec-des-données-dabondance.html pour des informations plus détaillées sur le traitement de la surdispersion avec des données d’abondance d’espèces.

À vous de jouer !
h5p

4.1.1 GLM Poisson : ray-grass dans les dunes

Comme premier exemple, nous traiterons de l’abondance du ray-grass Lolium perenne L., 1753 dans 20 sites différents de dunes en Hollande ainsi que des caractéristiques environnementales associées (jeux de données dune et dune.env du package {vegan}). Nous voulons établir une relation entre l’abondance de cette graminée et les caractéristiques du sol (épaisseur de la couche A1 de sable sous la couche organique du profil pédologique en cm et Moisture, l’humidité du sol sous forme d’une variable qualitative ordonnée avec les niveaux 1 < 2 < 4 < 5) ou de gestion des dunes (variable Management que nous remanions en deux modalités conservation et culture), voir ?vegan::dune pour plus de détails.

dune <- sbind_cols(
  read("dune", package = "vegan") |> sselect(Lolipere),
  read("dune.env", package = "vegan") |> sselect(A1, Moisture, Management)
) %>.%
  smutate(., Management = case_when(
    Management == "NM" ~ "conservation",
    .default = "culture") |> factor())
skimr::skim(dune)
Tableau 4.1: Data summary
Name dune
Number of rows 20
Number of columns 4
Key NULL
_______________________
Column type frequency:
factor 2
numeric 2
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
Moisture 0 1 TRUE 4 1: 7, 5: 7, 2: 4, 4: 2
Management 0 1 FALSE 2 cul: 14, con: 6

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
Lolipere 0 1 2.90 2.83 0.0 0.0 2.0 6.00 7.0 ▇▃▁▂▆
A1 0 1 4.85 2.18 2.8 3.5 4.2 5.73 11.5 ▇▂▁▁▁

Avec seulement 20 lignes dans le tableau, nous n’avons pas beaucoup de données (notez que c’est une situation qui se rencontre malheureusement souvent en biologie). Nous verrons qu’il est quand même possible d’exploiter ce petit jeu de données. Voici le graphique en barres qui montre la distribution de l’abondance de L. perenne.

chart(data = dune, ~ Lolipere) +
  geom_bar() +
  labs(x = "Abondance [nbr de plants/quadrat]",
       y = "Nombre de sites")

Nous avons huit sites où la graminée est absente. Ensuite il semble qu’il y ait un mode aux alentours de six plants par quadra avec quatre sites concernés. Comment se distribuent les sites en fonction de l’humidité du sol et du mode de gestion ?

table(Humidité = dune$Moisture, Gestion = dune$Management) |>
  tabularise()

Humidité

Gestion

conservation

culture

Total

1

Count

1 (5.0%)

6 (30.0%)

7 (35.0%)

Mar. pct (1)

16.7% ; 14.3%

42.9% ; 85.7%

2

Count

1 (5.0%)

3 (15.0%)

4 (20.0%)

Mar. pct

16.7% ; 25.0%

21.4% ; 75.0%

4

Count

0 (0.0%)

2 (10.0%)

2 (10.0%)

Mar. pct

0.0% ; 0.0%

14.3% ; 100.0%

5

Count

4 (20.0%)

3 (15.0%)

7 (35.0%)

Mar. pct

66.7% ; 57.1%

21.4% ; 42.9%

Total

Count

6 (30.0%)

14 (70.0%)

20 (100.0%)

(1) Columns and rows percentages

Avec si peu de données, nous pouvons nous attendre à des effectifs faibles. Il n’y a même pas de cas de niveau d’humidité 4 en zone de conservation et un seul cas pour les humidités 1 ou 2, mais pour le reste, on a de la donnée. Comment l’abondance de L. perenne se distribue par rapport à l’épaisseur de la couche A1 ?

chart(data = dune, Lolipere ~ A1) +
  geom_point() +
  labs(x = "Épaisseur de la couche A1 [cm]",
       y = "Abondance [nbr de plants/quadrat]")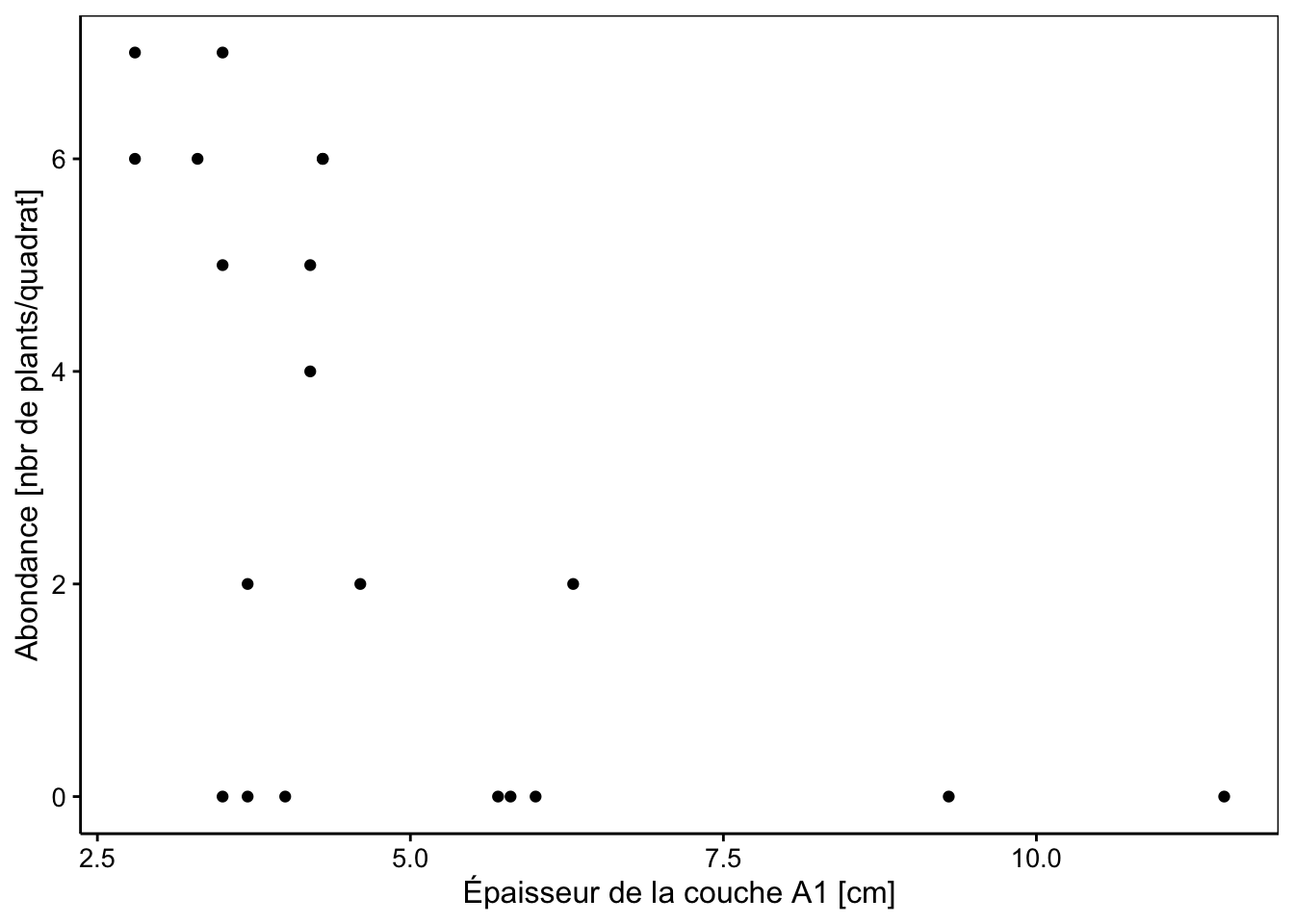

Ce genre de graphique est assez classique pour des données d’abondance en fonction d’une variable quantitative. C’est loin d’être un beau nuage de points bien étiré que nous avons l’habitude de rencontrer en régression linéaire. Nous avons quand même les abondances les plus importantes qui se retrouvent pour des épaisseurs A1 faibles. Commençons par un modèle simple relatif à cette dernière variable A1 uniquement. Nous choisissons une GLM de type Poisson.

dune_glm <- glm(data = dune, Lolipere ~ A1, family = poisson)
summary(dune_glm) |> tabularise()

Modèle linéaire généralisé

log⁡(E(Lolipere⁡))=α+β(A1⁡)\log ({ E( \operatorname{Lolipere} ) }) = \alpha + \beta_{}(\operatorname{A1})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

3.569

0.591

6.04

1.53·10-09

***

β\beta_{}

-0.607

0.154

-3.94

8.11·10-05

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Poisson: 1)

Déviance totale : 68.58 pour 19 degrés de liberté

Déviance résiduelle : 41.44 pour 18 degrés de liberté

AIC : 85.75 - Nombre d’itérations de la fonction de score de Fisher: 5

Il n’y a pas ici d’ANOVA pour déterminer si le modèle est significatif, mais le critère d’Akaiké est renseigné (AIC = 85.75, pratique pour comparer différents modèles ajustés dans les mêmes données). Les tests t sur les paramètres qui les comparent à des distributions de Student dans le modèle linéaire sont ici remplacés par des tests z par rapport à des distributions Normales. Le principe est le même. Pour un paramètre \(\alpha\) ou \(\beta_i\) H0 : \(\beta_i = 0\) et H1: \(\beta_i \neq 0\). L’ordonnée à l’origine et la pente sont tous les deux significativement différents de zéro au seuil \(\alpha\) de 5%.

Ensuite, il est précisé que le paramètre de dispersion \(\phi\) est fixé à 1 dans une GLMavec famille Poisson. Vérifions ce que nous obtenons avec nos données en divisant la déviance résiduelle par ses degrés de liberté = 41.44 / 18 = 2.3 >> 1. Nous sommes dans une situation de surdispersion. Ajustons un modèle quasi-Poisson à la place.

dune_glm_quasi <- glm(data = dune, Lolipere ~ A1, family = quasipoisson)
summary(dune_glm_quasi) |> tabularise()

Modèle linéaire généralisé

log⁡(E(Lolipere⁡))=α+β(A1⁡)\log ({ E( \operatorname{Lolipere} ) }) = \alpha + \beta_{}(\operatorname{A1})

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

3.569

0.771

4.63

0.000209

***

β\beta_{}

-0.607

0.201

-3.02

0.007367

**

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Quasi-Poisson: 1.704)

Déviance totale : 68.58 pour 19 degrés de liberté

Déviance résiduelle : 41.44 pour 18 degrés de liberté

AIC : NA - Nombre d’itérations de la fonction de score de Fisher: 5

Cette fois-ci, la dispersion \(\phi\) est estimée à 1.7 et c’est cette valeur qui est utilisée pour modéliser la variance en fonction des valeurs prédites dans les calculs. Notez que les estimateurs des paramètres ont changé complètement. Notez aussi que les valeurs p des tests z sont plus élevées. En fait le modèle quasi-Poisson est moins robuste que le modèle Poisson. Cela signifie qu’il détectera moins facilement si un paramètre est significativement différent de zéro ou non. C’est particulièrement ennuyeux lorsque nous avons peu de données à disposition comme ici. Enfin, le maximum de vraisemblance n’est pas calculable, et donc l’AIC. C’est aussi embêtant.

En cas de surdispersion ou sousdispersion, il est plutôt conseillé de revoir le modèle Poisson (les variables explicatives du modèle) plutôt que de se lancer directement dans un quasi-Poisson. On peut tester des transformations de la variable quantitative explicative (essayer la transformation log en particulier), ou ajouter/enlever des termes au modèle. Ici, nous allons introduire nos variables Moisture et Management. Vu le peu de données à dispositions, nous préférons ne pas introduire de termes d’interactions (ce qui ne veut pas dire qu’ils n’existent pas !)

dune_glm2 <- glm(data = dune, Lolipere ~ A1 +  Management + Moisture,
  family = poisson)
summary(dune_glm2) |> tabularise()

Modèle linéaire généralisé

log⁡(E(Lolipere⁡))=α+β1(A1⁡)+β2(Management⁡culture⁡)+β3(Moisture⁡.L⁡)+β4(Moisture⁡.Q⁡)+β5(Moisture⁡.C⁡)\log ({ E( \operatorname{Lolipere} ) }) = \alpha + \beta_{1}(\operatorname{A1}) + \beta_{2}(\operatorname{Management}_{\operatorname{culture}}) + \beta_{3}(\operatorname{Moisture}_{\operatorname{.L}}) + \beta_{4}(\operatorname{Moisture}_{\operatorname{.Q}}) + \beta_{5}(\operatorname{Moisture}_{\operatorname{.C}})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

0.454

1.002

0.453

0.6508

β1\beta_{1}

-0.344

0.159

-2.167

0.0302

*

β2\beta_{2}

1.921

0.734

2.616

0.0089

**

β3\beta_{3}

-1.066

0.431

-2.475

0.0133

*

β4\beta_{4}

0.153

0.460

0.333

0.7394

β5\beta_{5}

0.732

0.517

1.416

0.1567

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Poisson: 1)

Déviance totale : 68.58 pour 19 degrés de liberté

Déviance résiduelle : 14.17 pour 14 degrés de liberté

AIC : 66.48 - Nombre d’itérations de la fonction de score de Fisher: 6

La dispersion observée est de 14.17/14 = 1.01 ≈ 1. Nous avons maintenant bien la valeur attendue. Concernant l’AIC, elle vaut 66.5 contre 85.8 dans notre premier modèle. Donc notre dernier modèle est incontestablement meilleur. Pour analyser les paramètres, nous devons nous rappeler que les matrices de contraste fonctionnent aussi en GLM. Management étant une variable facteur, les contrastes par défaut sont des contrastes traitement. Le modèle est ajusté pour le premier niveau qui est conservation (les zones protégées). Le paramètre \(\beta_2\) indique le décalage pour les sites en culture. Ce décalage est positif, mais comment l’interpréter ? Résoudre l’équation du modèle nous aide à comprendre (ceci n’est pas l’équation générale du modèle, mais une version qui correspond au dernier modèle étudié).

\[ log(\hat{y}) = \alpha + \beta_1\ x + \beta_i\ I_j \]

avec :

  • \(\hat{y}\) la variable réponse prédite

  • \(\alpha\) l’ordonnée à l’origine

  • \(\beta_1\) la pente pour une variable quantitative \(x\)

  • \(\beta_i\) les paramètres relatifs aux contrastes définis pour les différentes variables qualitatives transformées en variables indicatrices \(I_j\)

Vous noterez le log qui correspond à la fonction de lien. Mais ce qui nous intéresse, c’est \(\hat{y}\) directement. Donc, on peut réécrire l’équation comme ceci :

\[ \hat{y} = e^{\alpha + \beta_1\ x + \beta_i\ I_j} = e^{\alpha} \cdot e^{\beta_1\ x} \cdot e^{\beta_2\ I_1} \cdot ... \]

Vous voyez maintenant pourquoi les modèles avec fonctions de lien log sont considérés comme multiplicatifs, parce qu’une fois transformés, ils font apparaître la multiplication des termes au lieu de leur addition. Si un paramètre \(\beta_i\) vaut zéro alors \(e^{\beta_i}\) vaut un et le terme ne joue plus puisqu’il multiplie la valeur par un. Aussi, nous devons considérer l’exponentielle des paramètres. Donc, l’effet culture se marque comme \(e^{\beta_2} = e^{1.92} = 6.82\). Donc, en culture, l’abondance de L. perenne est 6.82 fois plus abondante.

Pour interpréter \(\beta_3\) à \(\beta_5\), nous devons nous souvenir que Moisture est un facteur ordonné et que les matrices de contraste pour ce type de variable sont polynomiales faisant ressortir un effet linéaire (\(\beta_3\)), conique (\(\beta_4\)) et quadratique (\(\beta_5\)). Ici, des trois, seul l’effet linéaire est significatif au seuil \(\alpha\) de 5%. Le paramètre est estimé à -1.07 et donc l’effet est de \(e^{-1.07} = 0.34\). Notez au passage que des paramètres négatifs mènent à des multiplications par des nombres positifs inférieurs à un, soit à des divisions. Ainsi, cela signifie que l’abondance de L. perenne diminue avec le niveau d’humidité, ce qui nous mène à diviser son abondance par un terme qui est exponentiellement proportionnel avec le niveau d’humidité (oui, je sais, ce n’est pas facile… vous avez intérêt à relire la dernière phrase len-te-ment !).

Enfin, \(\beta_1\) est également significatif au seuil \(\alpha\) de 5% et est négatif. Cela signifie que l’abondance de L. perenne diminue avec l’augmentation de la couche A1 comme \(e^{-0.34} = 0.71\). Nous l’avions déjà remarqué sur le graphique. L’ordonnée à l’origine \(\alpha\) n’est, par contre, plus significativement différente de zéro ici.

Ce modèle pourrait être simplifié. Nous procéderons comme pour le modèle linéaire en comparant les critères d’Akaiké comme nous l’avons fait entre nos deux modèles Poissons précédents, ou en utilisant un test \(\chi^2\) équivalent de l’ANOVA de comparaison dans le cas de modèles linéaires imbriqués. L’AIC était en faveur du second modèle, que nous donne le test \(\chi^2\) ?

anova(dune_glm, dune_glm2, test = "Chisq") |> tabularise()
# Warning in tidy.anova(data): The following column names in ANOVA output were
# not recognized or transformed: Resid..Df, Resid..Dev, Deviance

Analyse de la déviance
Modèle 1: Lolipere ~ A1
Modèle 2: Lolipere ~ A1 + Management + Moisture

Modèle

Resid..Df

Resid..Dev

Ddl

Deviance

Valeur de p

Modèle 1

18

41.4

Modèle 2

14

14.2

4

27.3

1.75·10-05

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Il faut avouer que c’est un peu déroutant d’utiliser la fonction anova() ici avec un argument test = "Chisq" pour faire un test de \(\chi^2\) , mais c’est comme cela que les concepteurs de R l’ont décidé. Le tableau obtenu est plus correct, car intitulé “analyse de la déviance” et pas “ANOVA” ou “analyse de la variance”. L’interprétation est la même : H0 : les deux modèles sont équivalents versus H1 : le modèle le plus complexe est le meilleur. Ici, nous rejetons H0 au seuil \(\alpha\) de 5% en faveur du modèle le plus complexe (le second encore une fois). Voici notre modèle paramétré :

\[ \log ({ \widehat{E( \operatorname{Lolipere} )} }) = 0.45 - 0.34(\operatorname{A1}) + 1.92(\operatorname{Management}_{\operatorname{culture}}) - 1.07(\operatorname{Moisture}_{\operatorname{.L}}) + 0.15(\operatorname{Moisture}_{\operatorname{.Q}}) + 0.73(\operatorname{Moisture}_{\operatorname{.C}}) \]

Les prédictions d’abondances se font en utilisant predict(…, type = "response").

new_sites <- dtbl_rows(
 ~A1, ~Moisture, ~Management,
   3,         1, "conservation",
   3,         1, "culture",
   5,         2, "conservation",
   5,         2, "culture"
) %>.%
  mutate(., Moisture   = ordered(Moisture, levels = c(1, 2, 4, 5)),
            Management = factor(Management))
# Probabilité d'abondance de L. perenne en ces sites
new_sites$pred <- predict(dune_glm2,
  newdata = new_sites, type = "response")
new_sites
# # A tibble: 4 × 4
#      A1 Moisture Management    pred
#   <dbl> <ord>    <fct>        <dbl>
# 1     3 1        conservation 1.05 
# 2     3 1        culture      7.18 
# 3     5 2        conservation 0.543
# 4     5 2        culture      3.71

Le modèle prédit pour une culture avec un sol ayant une épaisseur A1 de 3 cm et une humidité de 1 environ sept plants par quadrats. Pour les mêmes caractéristiques, il en prédit un seul en site de conservation. Pour finir, voici un graphique qui permet de mieux comprendre. Comparez les prédictions avec les valeurs observées dans ce graphique :

chart(data = dune, Lolipere ~ A1 %size=% Moisture %col=% Management) +
  geom_point(alpha = 0.7) +
  labs(x = "Épaisseur de la couche A1 [cm]",
       y = "Abondance [nbr de plants/quadrat]")

Nous voyons bien que le ray-grass n’est abondant (ou même présent) qu’en zone de culture et que l’humidité faible et l’épaisseur faible de la couche A1 sont nécessaires pour qu’on le trouve en quantité. Les données restent un peu limitées pour bien mettre en évidence les différents effets et il faudrait mesurer plus de sites pour confirmer ces résultats.

4.1.2 GLM binomiale avec proportions : maturation d’ovocytes

L’action de l’hypoxanthine sur l’inhibition de la maturation d’ovocytes nus de souris est étudiée. Voici les résultats :

ovo <- dtbl_rows(
  ~hypo, ~mat, ~tot,
      4,    0,   32,
      3,    3,   23,
      2,   12,   24,
      1,   24,   32,
    0.5,   26,   29,
   0.25,   28,   30,
      0,   35,   35
) %>.%
  mutate(., prop = mat/tot)

chart(data = ovo, prop ~ hypo) +
  geom_point() +
  labs(x = "Hypoxanthine [µM]",
       y = "Fraction d'ovocytes matures")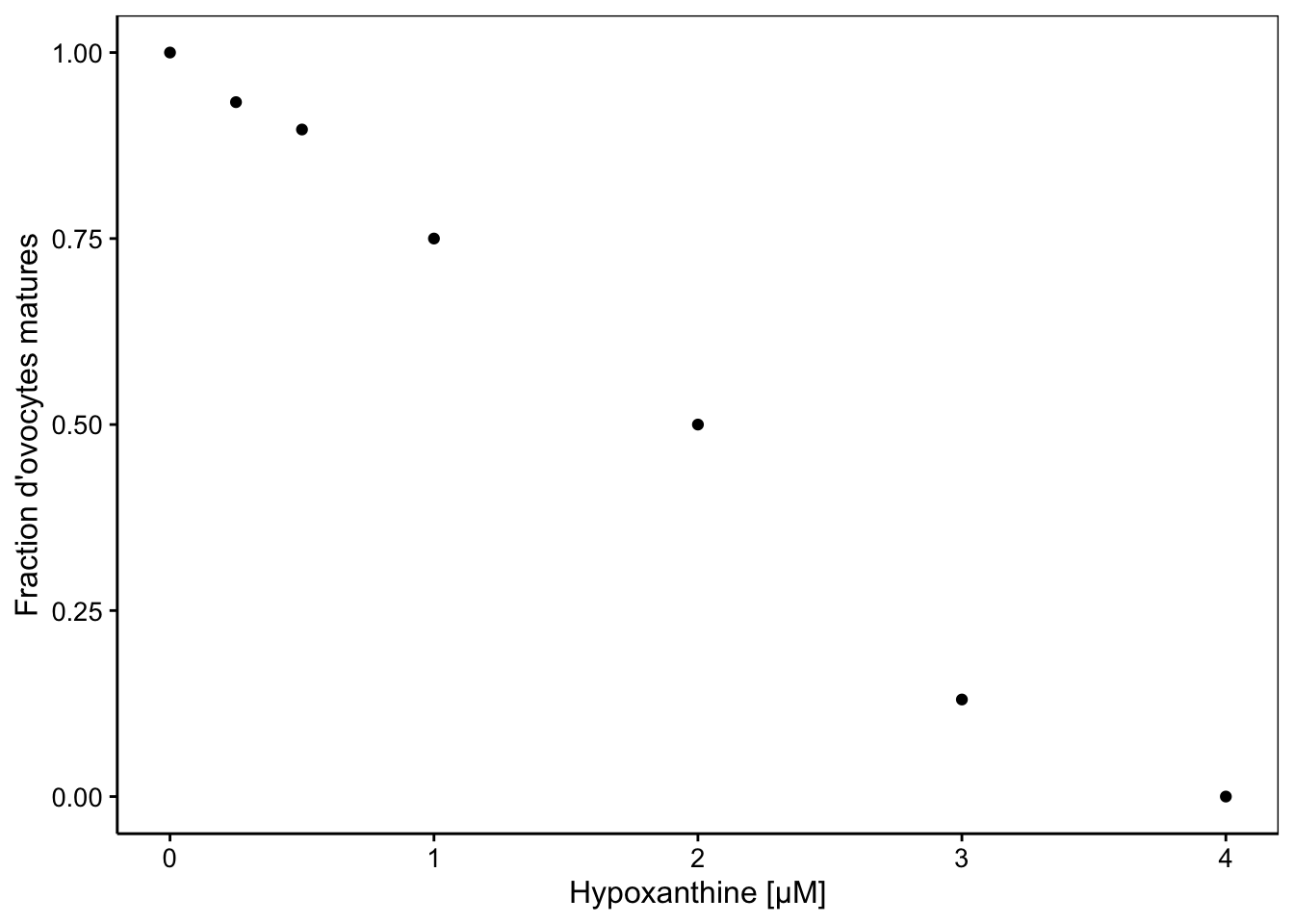

La GLM binomiale peut être utilisée ici avec une fonction de lien logit qui ajustera une courbe logistique en forme de S dans ces données.

ovo_glm <- glm(data = ovo, prop ~ hypo,
  family = binomial, weights = ovo$tot)
summary(ovo_glm) |> tabularise()

Modèle linéaire généralisé

log⁡[P(prop⁡=1⁡)1−P(prop⁡=1⁡)]=α+β(hypo⁡)\log\left[ \frac { P( \operatorname{prop} = \operatorname{1} ) }{ 1 - P( \operatorname{prop} = \operatorname{1} ) } \right] = \alpha + \beta_{}(\operatorname{hypo})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

3.27

0.407

8.03

9.54·10-16

***

β\beta_{}

-1.78

0.228

-7.83

4.80·10-15

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Binomiale: 1)

Déviance totale : 150.3 pour 6 degrés de liberté

Déviance résiduelle : 5.576 pour 5 degrés de liberté

AIC : 25.16 - Nombre d’itérations de la fonction de score de Fisher: 4

Il n’y a pas surdispersion (déviance résiduelle/degrés de liberté = 5.58/5 = 1.1 ≈ 1. Tous les paramètres sont significatifs au seuil \(\alpha\) de 5%. Notez que nous avons des proportions calculées sur des totaux différents pour chaque concentration. Le modèle en tient compte si nous indiquons ces totaux dans l’argument weights =. Une autre façon de renseigner cela au modèle est une forme un peu particulière. On lui donne une matrice de deux colonnes qui reprend le nombre de cas positifs et le total. Le modèle obtenu est le même.

ovo_glm_bis <- glm(data = ovo, cbind(mat, tot) ~ hypo,
  family = binomial)
summary(ovo_glm) |> tabularise()

Modèle linéaire généralisé

log⁡[P(prop⁡=1⁡)1−P(prop⁡=1⁡)]=α+β(hypo⁡)\log\left[ \frac { P( \operatorname{prop} = \operatorname{1} ) }{ 1 - P( \operatorname{prop} = \operatorname{1} ) } \right] = \alpha + \beta_{}(\operatorname{hypo})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

3.27

0.407

8.03

9.54·10-16

***

β\beta_{}

-1.78

0.228

-7.83

4.80·10-15

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Binomiale: 1)

Déviance totale : 150.3 pour 6 degrés de liberté

Déviance résiduelle : 5.576 pour 5 degrés de liberté

AIC : 25.16 - Nombre d’itérations de la fonction de score de Fisher: 4

Pour obtenir le graphique de ce modèle, nous pouvons utiliser stat_smooth().

chart(data = ovo, prop ~ hypo) +
  geom_point() +
  stat_smooth(method = "glm", method.args = list(family = binomial),
    formula = y ~ x, se = FALSE) +
  labs(x = "Hypoxanthine [µM]",
       y = "Fraction d'ovocytes matures")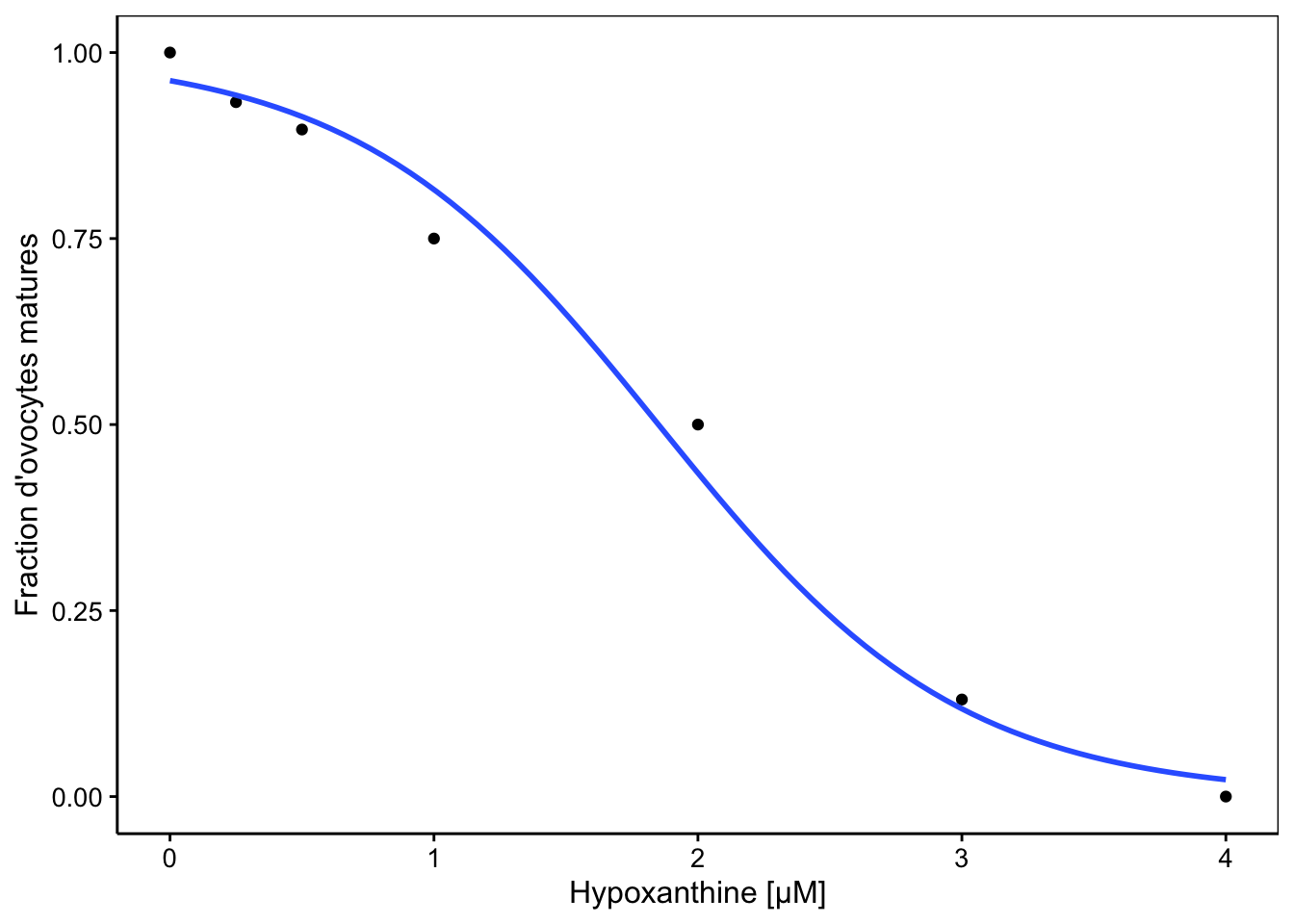

4.1.3 GLM binomiale avec variable binaire : acariens

Comme troisième exemple, nous allons travailler sur des données de présence/absence (variable binaire, donc qualitative à deux niveaux) de larves d’acariens dans des sols. Les jeux de données mite et mite.env du package {vegan} répertorient divers acariens dans des sols, ainsi que quelques-unes des propriétés de ces sols. Nous tranformons Oribatl1, les larves d’acariens Oribatidae en présence/absence et conservons WatrCont la teneur en eau en g/L ainsi que la topologie du sol (Topo, une variable qualitative à deux modalités Blanket ou Hummock) comme variables explicatives.

mite <- sbind_cols(
  read("mite", package = "vegan") |> sselect(Oribatl1),
  read("mite.env", package = "vegan") |> sselect(WatrCont, Topo)
) %>.%
  smutate(., Oribatl1 = case_when(
    Oribatl1 == 0 ~ "absent",
    .default = "present") |> factor())
skimr::skim(mite)
Tableau 4.2: Data summary
Name mite
Number of rows 70
Number of columns 3
Key NULL
_______________________
Column type frequency:
factor 2
numeric 1
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
Oribatl1 0 1 FALSE 2 abs: 40, pre: 30
Topo 0 1 FALSE 2 Bla: 44, Hum: 26

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
WatrCont 0 1 410.64 142.36 134.13 314.13 398.47 492.82 826.96 ▃▇▆▂▁

Le type de variable binaire réponse qui peut être traitée avec une GLM binomiale, outre la présence/absence est : sain/malade, vivant/mort, comportement A/comportement B, etc. Mais revenons à nos acariens, la présence/absence en fonction de la teneur en eaux varie comme ceci (normalement nous ferions ici des boîtes de dispersions parallèles, mais nous verrons plus tard pourquoi nous adoptons ce graphique un peu particulier ici) :

chart(data = mite, Oribatl1 ~ WatrCont | Topo) +
  geom_point(alpha = 0.5) +
  labs(x = "Teneur en eau [g/L]", y = "Larves d'acariens")

Qu’est-ce qu’on peut bien faire avec des données ayant ce genre de répartition ? En fait, si on considère une GLM binomiale, la transformation logit va nous calculer une transition de “absent” vers “présent” sous forme d’une courbe logistique en forme de S. Le modèle s’ajuste comme ceci :

mite_glm <- glm(data = mite, Oribatl1 ~ WatrCont * Topo,
  family = binomial)
summary(mite_glm) |> tabularise()

Modèle linéaire généralisé

log⁡[P(Oribatl1⁡=present⁡)1−P(Oribatl1⁡=present⁡)]=α+β1(WatrCont⁡)+β2(Topo⁡Hummock⁡)+β3(WatrCont⁡×Topo⁡Hummock⁡)\log\left[ \frac { P( \operatorname{Oribatl1} = \operatorname{present} ) }{ 1 - P( \operatorname{Oribatl1} = \operatorname{present} ) } \right] = \alpha + \beta_{1}(\operatorname{WatrCont}) + \beta_{2}(\operatorname{Topo}_{\operatorname{Hummock}}) + \beta_{3}(\operatorname{WatrCont} \times \operatorname{Topo}_{\operatorname{Hummock}})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

3.2198

1.63171

1.9733

0.0485

*

β1\beta_{1}

-0.0104

0.00406

-2.5542

0.0106

*

β2\beta_{2}

-0.0652

2.36999

-0.0275

0.9781

β3\beta_{3}

0.0042

0.00609

0.6897

0.4904

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Binomiale: 1)

Déviance totale : 95.61 pour 69 degrés de liberté

Déviance résiduelle : 67.69 pour 66 degrés de liberté

AIC : 75.69 - Nombre d’itérations de la fonction de score de Fisher: 5

Nous vérifions la dispersion \(\phi\) observée qui doit être proche de un avec ce modèle en divisant la déviance résiduelle par les degrés de liberté, soit 67.7/66 = 1.03 ≈ 1. Nous avons une AIC de 75.7. Les paramètres \(\alpha\) (ordonnées à l’origine) et \(\beta_1\) (teneur en eau) sont significatifs au seuil \(\alpha\) de 5%. Simplifions notre modèle en considérant que la topographie n’aurait aucun effet.

mite_glm2 <- glm(data = mite, Oribatl1 ~ WatrCont,
  family = binomial)
summary(mite_glm2) |> tabularise()

Modèle linéaire généralisé

log⁡[P(Oribatl1⁡=present⁡)1−P(Oribatl1⁡=present⁡)]=α+β(WatrCont⁡)\log\left[ \frac { P( \operatorname{Oribatl1} = \operatorname{present} ) }{ 1 - P( \operatorname{Oribatl1} = \operatorname{present} ) } \right] = \alpha + \beta_{}(\operatorname{WatrCont})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

3.7513

1.10988

3.38

0.000725

***

β\beta_{}

-0.0102

0.00277

-3.67

0.000241

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Binomiale: 1)

Déviance totale : 95.61 pour 69 degrés de liberté

Déviance résiduelle : 74.6 pour 68 degrés de liberté

AIC : 78.6 - Nombre d’itérations de la fonction de score de Fisher: 4

Les paramètres de ce second modèle simplifié sont tous également significatifs au seuil \(\alpha\) de 5%. Par contre, la dispersion observée augmente (74.6/68 = 1.1) sans être dramatique, mais l’AIC a augmenté à 78.6. Comparons également à l’aide d’un test \(\chi^2\) .

anova(mite_glm, mite_glm2, test = "Chisq")
# Analysis of Deviance Table
# 
# Model 1: Oribatl1 ~ WatrCont * Topo
# Model 2: Oribatl1 ~ WatrCont
#   Resid. Df Resid. Dev Df Deviance Pr(>Chi)  
# 1        66     67.694                       
# 2        68     74.596 -2  -6.9019  0.03172 *
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

La différence significative au seuil \(\alpha\) de 5% est aussi en faveur de conserver le modèle le plus complexe… Nous avons peut-être trop simplifié. Ajoutons Topo, mais cette fois-ci, sans les interactions.

mite_glm3 <- glm(data = mite, Oribatl1 ~ WatrCont + Topo,
  family = binomial)
summary(mite_glm3) |> tabularise()

Modèle linéaire généralisé

log⁡[P(Oribatl1⁡=present⁡)1−P(Oribatl1⁡=present⁡)]=α+β1(WatrCont⁡)+β2(Topo⁡Hummock⁡)\log\left[ \frac { P( \operatorname{Oribatl1} = \operatorname{present} ) }{ 1 - P( \operatorname{Oribatl1} = \operatorname{present} ) } \right] = \alpha + \beta_{1}(\operatorname{WatrCont}) + \beta_{2}(\operatorname{Topo}_{\operatorname{Hummock}})

Terme

Valeur estimée

Ecart type

Valeur de z

Valeur de p

α\alpha

2.56361

1.22983

2.08

0.03711

*

β1\beta_{1}

-0.00869

0.00295

-2.94

0.00324

**

β2\beta_{2}

1.52715

0.61449

2.49

0.01295

*

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

(Paramètre de dispersion pour une famille Binomiale: 1)

Déviance totale : 95.61 pour 69 degrés de liberté

Déviance résiduelle : 68.17 pour 67 degrés de liberté

AIC : 74.17 - Nombre d’itérations de la fonction de score de Fisher: 5

C’est beaucoup mieux avec une bonne dispersion et l’AIC de 74.2 le plus petit des trois. Tous les paramètres sont significativement différents de zéro au seuil \(\alpha\) de 5%.

anova(mite_glm, mite_glm3, test = "Chisq")
# Analysis of Deviance Table
# 
# Model 1: Oribatl1 ~ WatrCont * Topo
# Model 2: Oribatl1 ~ WatrCont + Topo
#   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
# 1        66     67.694                     
# 2        67     68.169 -1 -0.47444    0.491

Nous ne rejetons pas H0 pour le test de comparaison du modèle un avec le troisième, indiquant donc que la simplification par élimination du terme d’interaction nous donne un modèle équivalent au modèle complet. Nous conservons ce troisième et dernier modèle. Le voici paramétré :

\[ \log\left[ \frac { \widehat{P( \operatorname{Oribatl1} = \operatorname{present} )} }{ 1 - \widehat{P( \operatorname{Oribatl1} = \operatorname{present} )} } \right] = 2.56 - 0.0087(\operatorname{WatrCont}) + 1.53(\operatorname{Topo}_{\operatorname{Hummock}}) \]

Nous voudrions obtenir des prédictions de ce modèle ou le représenter sur un graphique et pouvoir interpréter ses paramètres. Mais ici, nous avons la variable réponse qui est transformée logit. Il faut donc appliquer une transformation inverse. Mais au fait, qu’est-ce \(P(\operatorname{Oribatil1=present})\) dans les équations ? C’est la probabilité d’observer une ou plusieurs larves d’acarien dans un échantillon, connaissant sa topographie et son degré d’humidité. Le calcul est plus compliqué, mais heureusement, la fonction predict(..., type = "response") le fait pour nous. Voici, par exemple, un nouveau tableau de teneurs en eau et topologies dans new_soils pour lequel nous voulons prédire les probabilités d’y observer des larves d’acariens :

new_soils <- dtbl_rows(
 ~WatrCont, ~Topo,
       150, "Blanket",
       500, "Blanket",
       800, "Blanket",
       200, "Hummock",
       400, "Hummock"
)
# Probabilité de larves d'acariens pour ces sols
new_soils$P <- predict(mite_glm3,
  newdata = new_soils, type = "response")
new_soils
# # A tibble: 5 × 3
#   WatrCont Topo         P
#      <dbl> <chr>    <dbl>
# 1      150 Blanket 0.779 
# 2      500 Blanket 0.144 
# 3      800 Blanket 0.0122
# 4      200 Hummock 0.913 
# 5      400 Hummock 0.649

De plus, chart() combiné à stat_smooth() permet de visualiser notre modèle (on y voit bien la forme en S de la courbe logistique) :

# Transformer la variable présence/absence en 0/1 d'abord
mutate(mite, Ori = as.numeric(Oribatl1 == "present")) %>.%
  chart(data = ., Ori ~ WatrCont %col=% Topo) +
    geom_point(alpha = 0.5) +
    stat_smooth(
      method = "glm",
      method.args = list(family = binomial),
      formula = y ~ x,
      se = TRUE) +
  labs(x = "Teneur en eau [g/L]", y = "Probabilité de présence")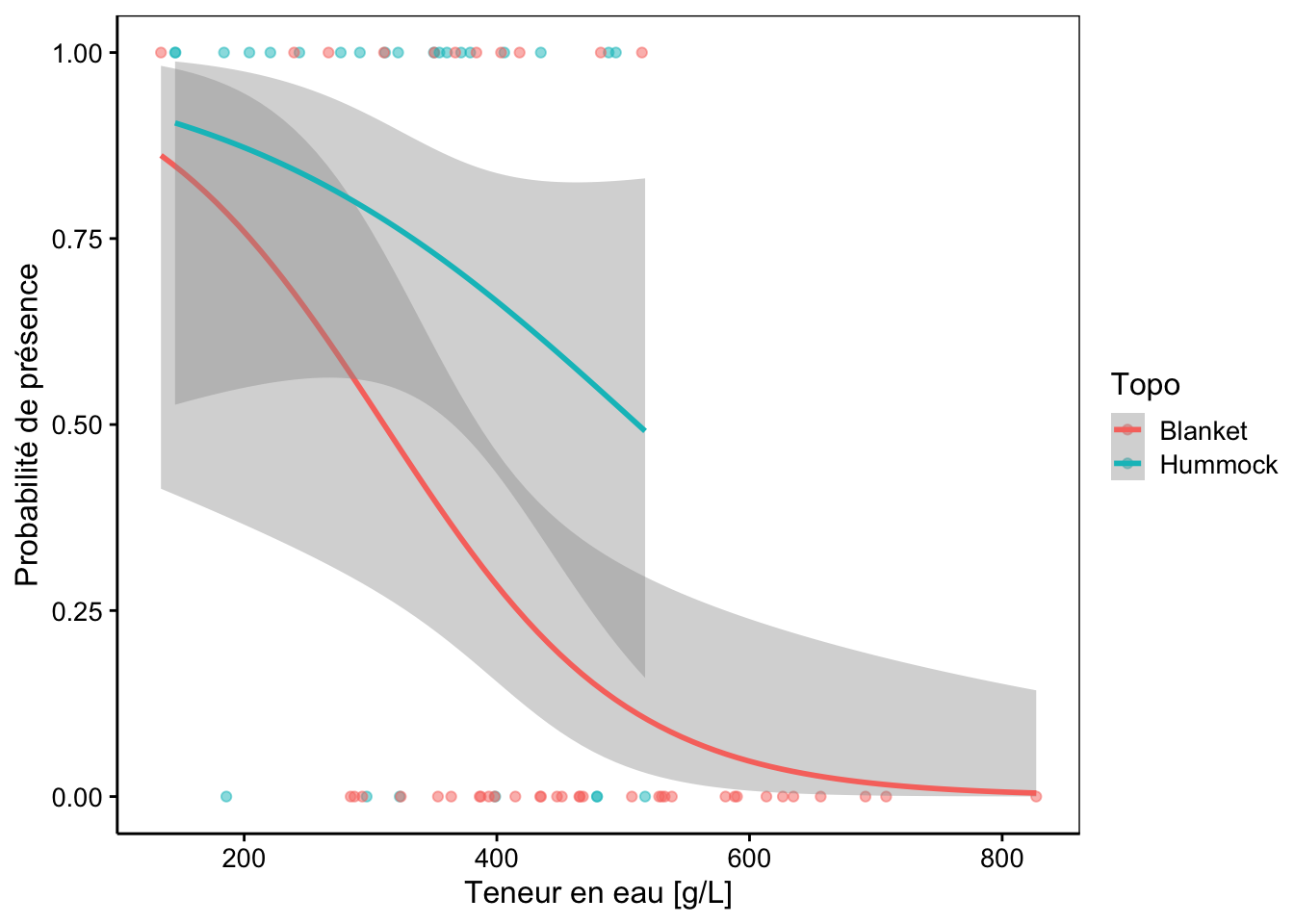

À vous de jouer !

Effectuez maintenant les exercices du tutoriel B04La_glm (Modèle linéaire généralisé).

BioDataScience2::run("B04La_glm")

  1. La GLM log-Normale (glm(data = …, y ~ x, family = gaussian(link = "log")) n’est pas équivalente à un modèle linéaire (généralisé) où \(y\) aurait été préalablement transformé en log avec soit lm(data = …, log(y) ~ x), soit glm(data = …, log(y) ~ x, family = gaussian) parce que dans le premier cas, l’erreur (la déviance des résidus) est calculée dans l’échelle non transformée alors que dans le second cas, l’erreur est aussi calculée dans l’échelle logarithmique. Selon la façon dont les résidus se distribuent, il faut donc utiliser l’une ou l’autre forme, mais elles ne sont ni synonymes, ni librement interchangeables.↩︎