3.4 ANCOVA

Avant l’apparition du modèle linéaire, une version particulière d’un mélange de régression linéaire et d’une ANOVA avec une variable indépendante quantitative et une autre variable indépendante qualitative s’appelait une ANCOVA (ANalyse de la COVariance). Un tel modèle d’ANCOVA peut naturellement également se résoudre à l’aide de la fonction lm() qui, en outre, peut faire bien plus. Nous allons maintenant ajuster un tel modèle à titre de première application concrète de tout ce que nous venons de voir sur le modèle linéaire et sur les matrices de contrastes.

À vous de jouer !
h5p

3.4.1 Oursins plus ou moins lourds

Commençons avec un jeu de données que vous connaissez bien : les oursins d’élevage comparés aux oursins sauvages pêchés en Bretagne. Nous voulons déterminer si la masse squelettique skeleton par rapport à la masse totale weight dépend de leur environnement (variable origin ; artificiel pour "Culture" versus naturel pour "Pêcherie"). Nous nous intéressons ici essentiellement aux oursins adultes dont la masse totale est supérieure ou égale à 30g (oursins à taille commercialisable). Nous prenons soin d’éliminer les valeurs manquantes pour la variable skeleton avant toute chose avec sdrop_na().

SciViews::R("model", lang = "FR")
read("urchin_bio", package = "data.io") %>.%
  sdrop_na(., skeleton) ->
  urchin
chart(data = urchin, skeleton ~ weight %col=% origin) +
  geom_point() +
  geom_vline(xintercept = 30, col = "darkgray", lty = 2)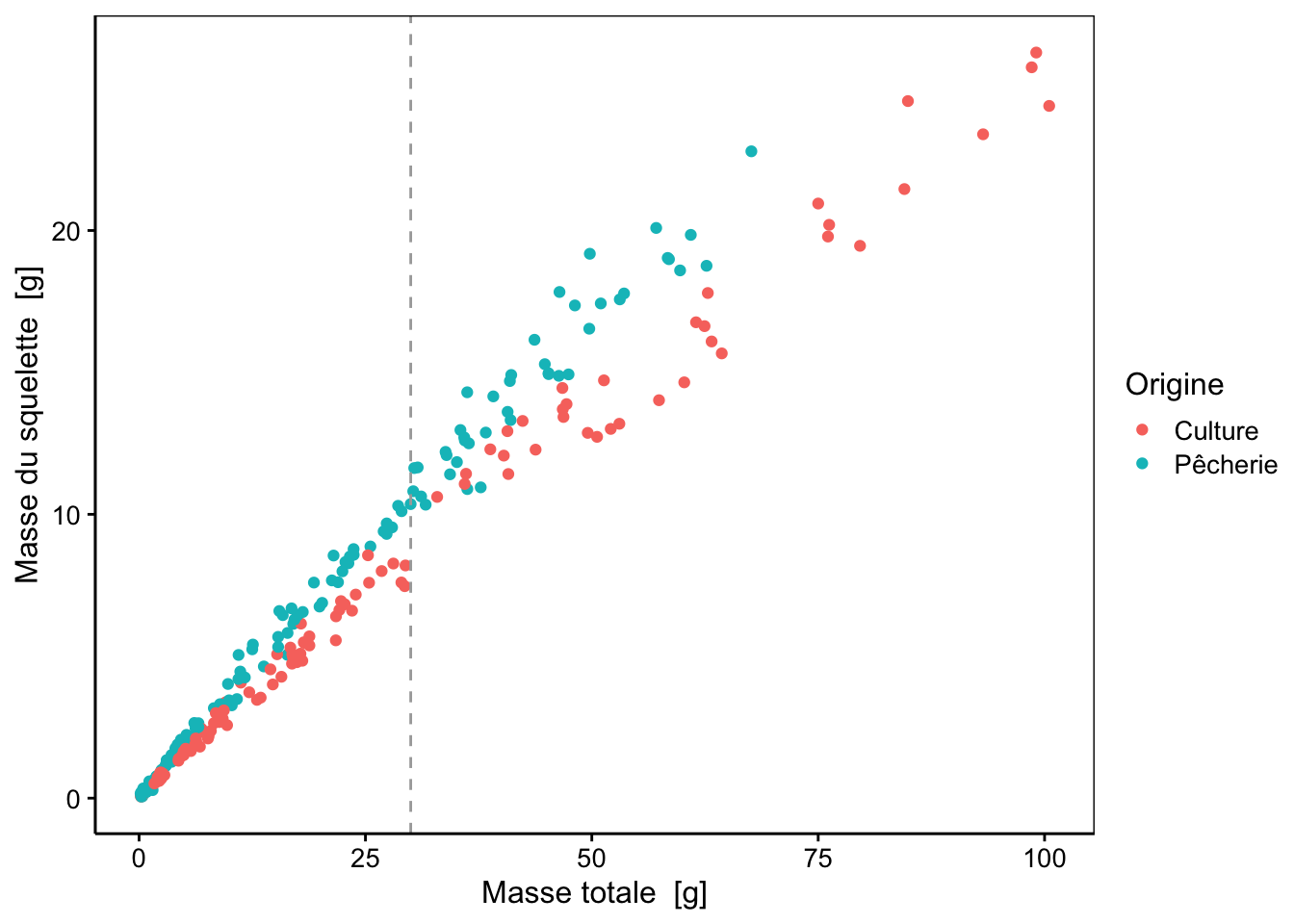

Sur le graphique, nous voyons très clairement une différence selon l’origine. Nous voyons aussi que les petits et les grands oursins semblent légèrement différer (à gauche et à droite du trait pointillé gris). Mais partout, les oursins pêchés ont un squelette plus lourd à masse totale équivalente. Nous pouvons imaginer ici des droites qui diffèrent par leurs pentes. Nous pouvons ajuster une droite différente pour chacune des deux sous-populations, mais comment déterminer si les deux pentes sont significativement différentes ? Le modèle linéaire permet de le faire. Tout comme pour l’ANOVA, utiliser * dans la formule permet de tester l’interaction entre les deux variables. Nous allons donc ajuster un modèle linéaire avec des interactions entre weight et origin. Si nous ne spécifions pas la matrice de contrastes à utiliser, c’est celle par défaut, soit les contrastes de type traitement qui seront utilisés. Notez aussi l’utilisation de l’argument subset= de lm() pour sélectionner un sous-ensemble des données.

urchin_lm <- lm(data = urchin, skeleton ~ weight * origin, subset = weight >= 30)
# Voici comment faire le graphique de ce modèle linéaire
chart(data = sfilter(urchin, skeleton > 10), skeleton ~ weight %col=% origin) +
  geom_point() +
  stat_smooth(method = "lm", formula = y ~ x)

Le résumé du modèle nous donne des informations utiles :

summary(urchin_lm)
# 
# Call:
# lm(formula = skeleton ~ weight * origin, data = urchin, subset = weight >= 
#     30)
# 
# Residuals:
#      Min       1Q   Median       3Q      Max 
# -2.15894 -0.50374 -0.05948  0.62930  2.67912 
# 
# Coefficients:
#                        Estimate Std. Error t value Pr(>|t|)    
# (Intercept)            2.635101   0.554260   4.754 9.75e-06 ***
# weight                 0.226661   0.008803  25.747  < 2e-16 ***
# originPêcherie        -0.852076   0.899589  -0.947  0.34667    
# weight:originPêcherie  0.073522   0.018094   4.063  0.00012 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 1.014 on 73 degrees of freedom
# Multiple R-squared:  0.9353,  Adjusted R-squared:  0.9326 
# F-statistic: 351.6 on 3 and 73 DF,  p-value: < 2.2e-16

Le R2 de 0.93 est élevé. La valeur p de l’ANOVA est inférieure à 5% et le modèle est significatif. Avec une matrice de type traitement, le modèle est ajusté d’abord sur la sous-population correspondant au premier niveau de la variable factor origin, c’est-à-dire "Culture".

class(urchin$origin)
# [1] "factor"
levels(urchin$origin)
# [1] "Culture"  "Pêcherie"

(Intercept) est l’ordonnée à l’origine et weight est la pente pour cette droite relative aux oursins d’élevage.

Nous avons deux lignes supplémentaires dans le tableau du résumé. La ligne originPêcherie correspond au décalage de l’ordonnée à l’origine pour la droite relative à la sous-population "Pêcherie". Cela signifie que l’ordonnée à l’origine pour les oursins pêchés vaut : 2.635 - 0.852 = 1.783. La ligne weight:originPêcherie correspond au décalage de pente entre les deux sous-populations, soit une pente de 0.2267 + 0.0735 = 0.3002 pour "Pêcherie". Nous pouvons donc écrire les deux droites de régression linéaire comme suit :

\[skeleton_{Culture} = 2.64 + 0.23 \cdot weight_{Culture}\]

\[skeleton_{Pêcherie} = 1.78 + 0.30 \cdot weight_{Pêcherie}\]

Maintenant, regardons les tests t de Student pour chaque paramètre (colonnes t value et Pr(>|t|)) pour la valeur p du test (rappelez-vous que pour ce test, nous avons : H0 le paramètre vaut zéro et H1 le paramètre est différent de zéro). Tous les paramètres (on dit aussi coefficients) sont significativement différents de zéro, sauf le décalage de l’ordonnée à l’origine originePêcherie. Le tableau de l’ANOVA du modèle linéaire confirme que les deux variables ont un effet significatif, ainsi que leurs interactions (mais il ne dit rien concernant le décalage de l’ordonnée à l’origine… il n’apparaît jamais dans ce tableau) :

anova(urchin_lm)
# Analysis of Variance Table
# 
# Response: skeleton
#               Df Sum Sq Mean Sq F value    Pr(>F)    
# weight         1 964.34  964.34 937.606 < 2.2e-16 ***
# origin         1 103.67  103.67 100.797 2.151e-15 ***
# weight:origin  1  16.98   16.98  16.511 0.0001205 ***
# Residuals     73  75.08    1.03                      
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dans un cas comme celui-ci, nous pouvons simplifier le modèle en éliminant le décalage de l’ordonnée à l’origine. Mais comment faire ? Nous devons nous rappeler que la formule skeleton ~ weight * origin est en fait une abréviation pour skeleton ~ weight + origin + weight:origin. Retenez que, dans cette dernière formule, le terme origin indique que nous voulons un décalage de l’origine pour chaque niveau, et le terme weight:origin indique qu’un décalage de pentes est souhaité. Donc, pour éliminer le décalage d’origine du modèle, il suffit d’écrire skeleton ~ weight + weight:origin.

urchin_lm2 <- lm(data = urchin, skeleton ~ weight + weight:origin, subset = weight >= 30)
summary(urchin_lm2)
# 
# Call:
# lm(formula = skeleton ~ weight + weight:origin, data = urchin, 
#     subset = weight >= 30)
# 
# Residuals:
#      Min       1Q   Median       3Q      Max 
# -2.25359 -0.67406 -0.05519  0.61250  2.58774 
# 
# Coefficients:
#                       Estimate Std. Error t value Pr(>|t|)    
# (Intercept)           2.311644   0.436258   5.299 1.16e-06 ***
# weight                0.231547   0.007129  32.480  < 2e-16 ***
# weight:originPêcherie 0.057135   0.005292  10.797  < 2e-16 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 1.013 on 74 degrees of freedom
# Multiple R-squared:  0.9345,  Adjusted R-squared:  0.9327 
# F-statistic: 527.7 on 2 and 74 DF,  p-value: < 2.2e-16

Nous voyons qu’effectivement, le terme non significatif a disparu et il ne reste plus que les termes significatifs au seuil \(\alpha\) de 5%.

anova(urchin_lm2)
# Analysis of Variance Table
# 
# Response: skeleton
#               Df Sum Sq Mean Sq F value    Pr(>F)    
# weight         1 964.34  964.34  938.91 < 2.2e-16 ***
# weight:origin  1 119.73  119.73  116.57 < 2.2e-16 ***
# Residuals     74  76.00    1.03                      
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dans ce dernier modèle, les deux droites ont même ordonnée à l’origine 2.312 et des pentes respectives de 0.231 pour "Culture" et 0.231 + 0.057 = 0.288 pour "Pêcherie". Les équations deviennent donc :

\[skeleton_{Culture} = 2.31 + 0.23 \cdot weight_{Culture}\]

\[skeleton_{Pêcherie} = 2.31 + 0.29 \cdot weight_{Pêcherie}\]

Les interactions sont significatives dans notre modèle linéaire, que l’on le simplifie ou non. Cela démontre que les pentes sont différentes également de manière signification au seuil \(\alpha\) de 5%.

Jusqu’ici, nous avons repris les sorties “brutes” de R pour les tableaux et nous avons écrit des équations à la main. Mais nous pouvons aussi utiliser tabularise() et eq_() pour des équations en ligne ou eq__() pour des équations sur leur propre ligne, avec éventuellement use_coefs = TRUE et coef_digits = pour la version paramétrisée. Voici ce que cela donne pour notre modèle simplifié :

summary(urchin_lm2) |> tabularise()

Modèle linéaire

skeleton⁡=α+β1(weight⁡)+β2(weight⁡×weight⁡originPe^cherie⁡)+ϵ\operatorname{skeleton} = \alpha + \beta_{1}(\operatorname{weight}) + \beta_{2}(\operatorname{weight} \times \operatorname{weight}_{\operatorname{originPêcherie}}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

2.3116

0.43626

5.3

1.16·10-06

***

β1\beta_{1}

0.2315

0.00713

32.5

< 2·10-16

***

β2\beta_{2}

0.0571

0.00529

10.8

< 2·10-16

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-2.254, 2.588]

Ecart type des résidus : 1.013 pour 74 degrés de liberté

R2 multiple : 0.9345 - R2 ajusté : 0.9327

Statistique F : 527.7 pour 2 et 74 ddl - valeur de p : < 2.22e-16

\[\operatorname{\widehat{skeleton}} = 2.31 + 0.23(\operatorname{weight}) + 0.057(\operatorname{weight} \times \operatorname{weight}_{\operatorname{originPêcherie}})\]

Nous avons l’équation du modèle qui reprend les deux droites en même temps. Le terme \((weight \times weight_{originPêcherie})\) est le terme d’interactions. Rappelons-nous que les niveaux de la variable factor origin sont réencodés en variables muettes. \(weight_{originPêcherie}\) prend la valeur 0 pour la sous-population "Culture" et 1 pour la sous-population "Pêcherie". On retrouve donc bien nos calculs de pentes qui valent 0.23 pour la première et 0.23 + 0.057 = 0.29 pour la seconde.

Pour le modèle complet avec décalage de pente, l’équation paramétrée est :

\[\operatorname{\widehat{skeleton}} = 2.64 + 0.23(\operatorname{weight}) - 0.85(\operatorname{origin}_{\operatorname{Pêcherie}}) + 0.074(\operatorname{weight} \times \operatorname{origin}_{\operatorname{Pêcherie}})\] Ici, la variable muette est appelée \(origin_{Pêcherie}\), ce qui est un nom plus correct (une correction est sans doute nécessaire ici dans le moteur qui génère automatiquement les équations depuis le modèle dans le cas simplifié). Le principe est le même : la variable muette permet de prendre en compte le décalage de pente et d’ordonnée à l’origine, mais seulement dans le cas de la sous-population "Pêcherie" (valeur 1), puisque ces termes tombent pour "Culture"(valeur 0).

Nous n’avons pas encore réalisé l’analyse des résidus qui reste à faire également pour la partie régression linéaire de notre modèle. Voici l’analyse pour le modèle simplifié.

chart$residuals(urchin_lm2)

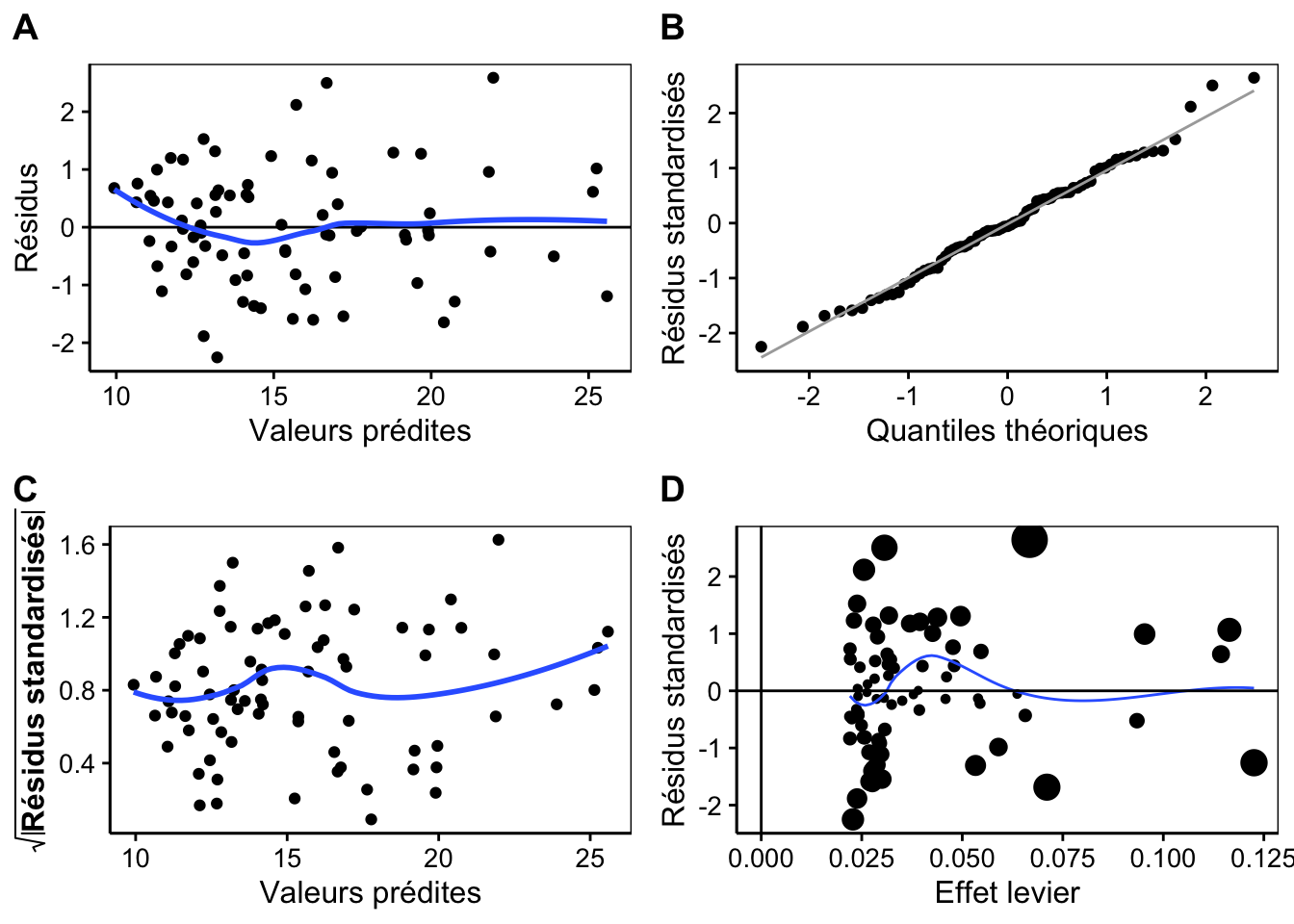
Nous observons des résidus d’étendue raisonnable par rapport aux valeurs prédites et une relativement bonne linéarité, sauf au début, mais cela correspond sans doute à une transition entre juvéniles et adultes (A). La distribution des résidus est proche de la Normale (B) et nous avons une relativement bonne homoscédasticité (C). Le seul souci ici est la présence de valeurs influentes à la distance de Cook élevée, dont certaines ont un grand effet de levier (D). Globalement, l’analyse des résidus est satisfaisante mais par sécurité, nous pourrions utiliser une méthode de régression plus robuste (non vue au cours, voir par exemple ?MASS::rlm()), ou étudier les points problématiques pour voir s’il n’y a pas lieu de les éliminer de l’analyse avec justification.

3.4.2 Bébés à la naissance

Afin d’explorer d’autres aspects du modèle linéaire, nous étudions maintenant un autre jeu de données. Analysons des données de masse de nouveaux nés en fonction du poids de la mère et du fait qu’elle fume ou non. Cette étude s’inspire de Verzani (2005). Nous avons une variable dépendante wt, la masse des bébés qui est quantitative, et deux variables indépendantes ou prédictives wt1, la masse de la mère, et smoke le fait que la mère fume ou non. Or la première de ces variables explicatives est quantitative (wt1) et l’autre (smoke) est une variable facteur à quatre niveaux (0 = la mère n’a jamais fumé, 1 = elle fume y compris pendant la grossesse, 2 = elle fumait, mais a arrêté à la grossesse, et 3 = la mère a fumé, mais a arrêté, et ce, bien avant la grossesse). La progression ici n’est pas logique, car si on classe les niveaux depuis le meilleur vers le moins bon pour la santé, nous devrions avoir 0 = jamais fumé, 3 = a arrêté depuis longtemps, 2 = a arrêté à la grossesse et 1 = continue de fumer. Un dernier niveau 9 = inconnu encode de manière inhabituelle les valeurs manquantes dans notre tableau de données (valeurs que nous éliminerons). Les masses des nouveau-nés et des mères sont dans des unités impériales (américaines) respectivement en “onces” et en “livres”. Nous les convertirons. Enfin, nous devons prendre soin de bien encoder la variable smoke comme une variable factor (ici nous ne considérons pas qu’il s’agit d’un facteur ordonné et nous voulons faire un contraste de type traitement avec comparaison à des mères qui n’ont jamais fumé). Un remaniement soigneux des données est donc nécessaire avant de pouvoir appliquer notre modèle ! C’est souvent le cas…

SciViews::R("model", lang = "fr")
babies <- read("babies", package = "UsingR")
tabularise$headtail(babies[, c("wt", "wt1", "smoke")])

wt

wt1

smoke

120

100

0

113

135

0

128

115

1

123

190

3

108

125

1

...

...

...

113

100

0

128

120

0

130

150

1

125

110

0

117

129

0

Premières et dernières 5 lignes d'un total de 1236

Il y a bien d’autres variables dans le jeu de données, que nous ne considérerons pas ici. Voyez help("babies", package = "UsingR") pour de plus amples informations. Nous allons maintenant remanier tout cela correctement.

# wt = masse du bébé à la naissance en onces et 999 = valeur manquante
# wt1 = masse de la mère à la naissance en livres et 999 = valeur manquante
# smoke = 0 (non), = 1 (oui), = 2 (jusqu'à grossesse),
#       = 3 (plus depuis un certain temps) and = 9 (inconnu)
#       transformé en 0 -> "never", 3 -> "before", 2 -> "until", 1 -> "during"
#       et NA = 9 (éliminé)
babies %>.% 
  sselect(., wt, wt1, smoke) %>.% # Garder seulement wt, wt1 & smoke
  sfilter(., wt1 < 999, wt < 999, smoke < 9) %>.% # Éliminer les valeurs manquantes
  smutate(., wt = wt * 0.02835) %>.% # Transformer le poids de livres en kg
  smutate(., wt1 = wt1 * 0.4536) %>.% # Idem de onces en kg
  smutate(., smoke = recode(smoke, "0" = "never", "3" = "before",
                                   "2" = "until", "1" = "during")) %>.%
  smutate(., smoke = factor(smoke,
    levels = c("never", "before", "until", "during"))) ->
  babies2 # Enregistrer le résultat dans babies2

tabularise$headtail(babies2)

wt

wt1

smoke

3.40200

45.3600

never

3.20355

61.2360

never

3.62880

52.1640

during

3.48705

86.1840

before

3.06180

56.7000

during

...

...

...

3.20355

45.3600

never

3.62880

54.4320

never

3.68550

68.0400

during

3.54375

49.8960

never

3.31695

58.5144

never

Premières et dernières 5 lignes d'un total de 1190

Description des données :

skimr::skim(babies2)
Tableau 3.1: Data summary
Name babies2
Number of rows 1190
Number of columns 3
Key NULL
_______________________
Column type frequency:
factor 1
numeric 2
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
smoke 0 1 FALSE 4 nev: 531, dur: 465, bef: 102, unt: 92

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
wt 0 1 3.39 0.52 1.56 3.06 3.4 3.71 4.99 ▁▃▇▅▁
wt1 0 1 58.30 9.49 39.46 51.82 56.7 62.60 113.40 ▅▇▁▁▁

L’idéal pour la variable smoke serait d’avoir autant d’items dans chaque niveau. Ce n’est pas le cas ici, mais nous ne pouvons pas faire grand-chose, sauf à éliminer des données dans niveaux les plus abondants, ce qui serait dommage. Nous allons maintenant réaliser quelques graphiques pertinents dans le contexte de notre analyse pour visualiser les données.

chart(data = babies2, wt ~ wt1 %col=% smoke) +
  geom_point() +
  xlab("wt1 : masse de la mère [kg]") +
  ylab("wt : masse du bébé [kg]")

chart(data = babies2, wt ~ smoke) +
  geom_boxplot() +
  ylab("wt : masse du bébé [kg]")

chart(data = babies2, wt1 ~ smoke) +
  geom_boxplot() +
  ylab("wt1 : masse de la mère [kg]")

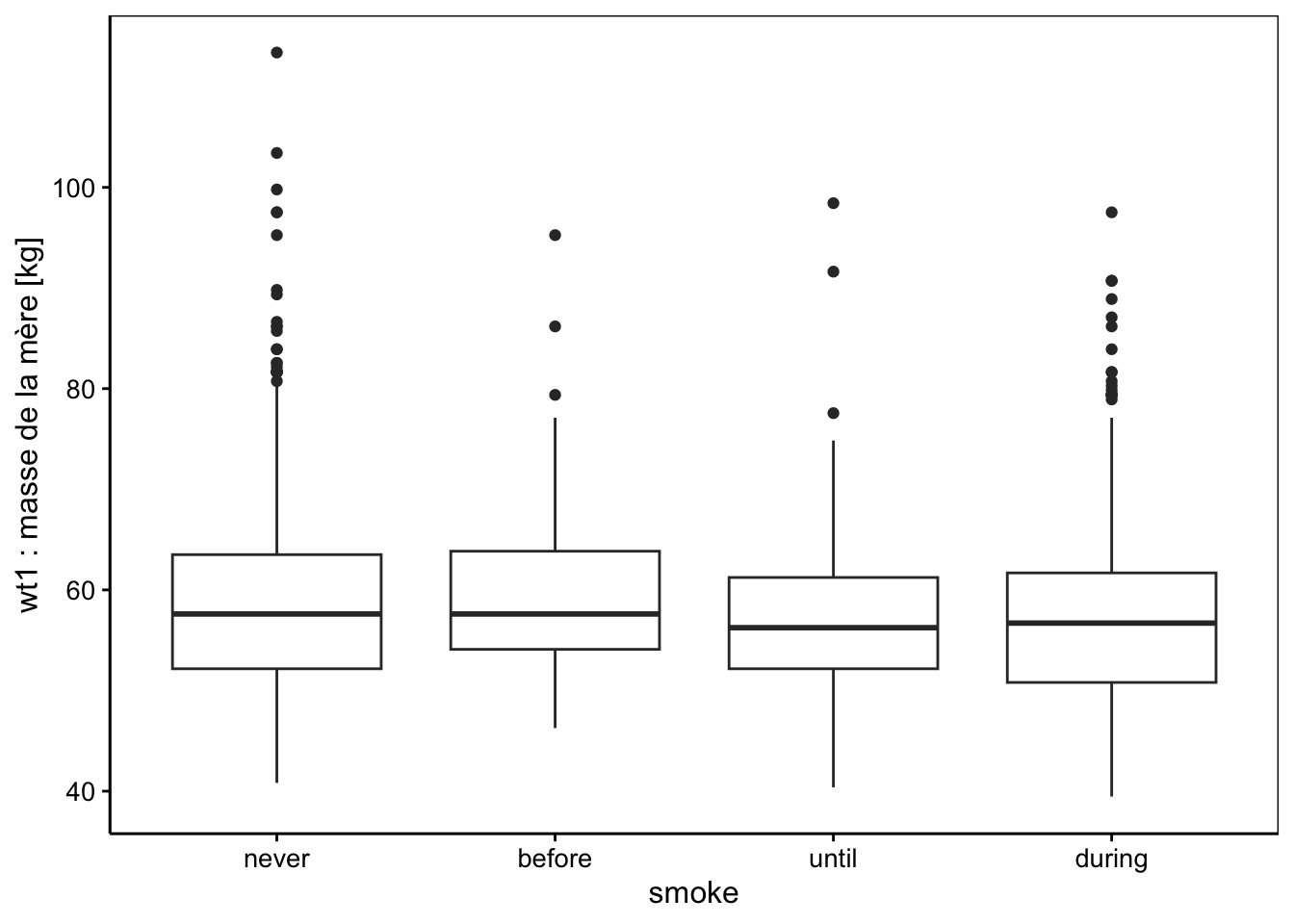
Avec les graphiques, nous ne voyons pas d’effet marquant. Peut-être la condition during de smoke (mère qui fume pendant la grossesse) mène-t-elle à des bébés moins gros, mais est-ce significatif ? Pour cela, ajustons notre modèle linéaire (alias ANCOVA) avec une matrice de traitement (choix par défaut pour une la variable factor smoke). Comme nous savons déjà utiliser lm(), nous sommes en tarrain connu : cela fonctionne exactement comme avant8.

# Modèle linéaire de type (anciennement) ANCOVA
babies2_lm <- lm(data = babies2, wt ~ smoke * wt1)
summary(babies2_lm) |> tabularise()

Modèle linéaire

wt⁡=α+β1(smoke⁡before⁡)+β2(smoke⁡until⁡)+β3(smoke⁡during⁡)+β4(wt1⁡)+β5(smoke⁡before⁡×wt1⁡)+β6(smoke⁡until⁡×wt1⁡)+β7(smoke⁡during⁡×wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{1}(\operatorname{smoke}_{\operatorname{before}}) + \beta_{2}(\operatorname{smoke}_{\operatorname{until}}) + \beta_{3}(\operatorname{smoke}_{\operatorname{during}}) + \beta_{4}(\operatorname{wt1}) + \beta_{5}(\operatorname{smoke}_{\operatorname{before}} \times \operatorname{wt1}) + \beta_{6}(\operatorname{smoke}_{\operatorname{until}} \times \operatorname{wt1}) + \beta_{7}(\operatorname{smoke}_{\operatorname{during}} \times \operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

3.00066

0.12833

23.3818

< 2·10-16

***

β1\beta_{1}

-0.03550

0.37138

-0.0956

9.24·10-01

β2\beta_{2}

0.90189

0.37139

2.4284

1.53·10-02

*

β3\beta_{3}

-0.30361

0.19693

-1.5417

1.23·10-01

β4\beta_{4}

0.00812

0.00215

3.7768

1.67·10-04

***

β5\beta_{5}

0.00118

0.00615

0.1914

8.48·10-01

β6\beta_{6}

-0.01534

0.00639

-2.4006

1.65·10-02

*

β7\beta_{7}

0.00115

0.00335

0.3446

7.30·10-01

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.957, 1.499]

Ecart type des résidus : 0.4992 pour 1182 degrés de liberté

R2 multiple : 0.08248 - R2 ajusté : 0.07705

Statistique F : 15.18 pour 7 et 1182 ddl - valeur de p : < 2.22e-16

anova(babies2_lm) |> tabularise()
Tableau 3.2:

Terme

Ddl

Somme des carrés

Carrés moyens

Valeur de Fobs.

Valeur de p

smoke

3

18.66

6.220

24.96

1.16·10-15

***

wt1

1

6.16

6.162

24.73

7.56·10-07

***

smoke:wt1

3

1.65

0.551

2.21

8.51·10-02

.

Résidus

1 182

294.50

0.249

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

L’analyse de variance (tableau du bas) montre que la masse de la mère a un effet significatif au seuil alpha de 5%, de même que la variable smoke. Par contre, il n’y a pas d’interactions entre les deux. Le fait de pouvoir mesurer des interactions entre variables qualitatives et quantitatives est ici bien évidemment un plus du modèle linéaire par rapport à ce qu’on pouvait faire avant !

Dans le tableau supérieur, nous avons le détail du modèle linéaire complet qui tient compte de la matrice de contrastes de type traitement choisie pour smoke (donc, comparaison à un modèle de base ajusté pour smoke == "never", mères n’ayant jamais fumé, premier niveau de la variable). Cette analyse est bien plus complète qu’une simple ANOVA, et nous voyons se dégager d’autres résultats lorsque les quatre conditions de smoke sont contrastées. Le résumé de l’analyse nous montre que la régression de la masse des bébés en fonction de la masse de la mère (ligne wt1 dans le tableau des coefficients), bien qu’étant significative, n’explique que 8% de la variance totale (le R2). Suite à l’examen du nuage de points plus haut, nous n’en sommes pas surpris.

Les coefficients \(\beta_1\), \(\beta_2\) et \(\beta_3\) des termes smoke == "before", smoke == "until" et smoke == "during" respectivement, sont les contrastes appliqués par rapport au contrôle (smoke == "never"). Ce sont les décalages des ordonnées à l’origine dans la régression du poids du bébé en fonction du poids de la mère, lorsque la matrice de contrastes de traitements est utilisée comme ici. Par exemple, pour smoke == "before", l’estimation de l’ordonnée à l’origine pour la sous-population de référence smoke == "never" est de 3.000 (paramètre \(\alpha\)) -0.0355, valeur de décalage estimé de \(\beta_1\) pour le terme smoke == "before", ce qui donne une ordonnée à l’origine pour la droite de la sous-population smoke == "before" de 2.965. Le même raisonnement peut être fait pour la sous-population smoke == "until" (3.000 + 0.902 = 3.902) et smoke == "during" (3.000 - 0.304 = 2.696).

Les coefficients \(\beta_5\), \(\beta_6\) et \(\beta_7\) correspondent aux termes d’interactions notés smokebefore:wt1, smokeuntil:wt1 et smokeduring:wt1 dans les sorties brutes de R (sans utiliser tabularise()), ou \(smoke_{before} \times wt1\), \(smoke_{until} \times wt1\) et \(smoke_{during} \times wt1\) dans les équations avec tabularise(). Concrètement, cela représente le décalage de la pente par rapport à la droite représentant le poids des bébés wt en fonction du poids de la mère wt1 dans la sous-population de référence smoke == "never" dont la pente \(\beta_4\) est estimée à 0.00812. Nous pouvons donc dire que la pente estimée pour la sous-population smoke == "before" est de 0.00812 + 0.00118 = 0.00930, pour la sous-population smoke == "until" elle est de 0.00812 - 0.0153 = -0.00718, et enfin pour la sous-population smoke == "during", elle est de 0.00812 + 0.00115 = 0.00927.

Bien. Mais maintenant, est-ce que ces décalages d’ordonnées à l’origine et de pente sont significatifs ? Nous regardons les tests t de Student sur la même ligne du tableau pour chacun des coefficients (H0: coefficient = 0, H1: coefficient ≠ 0). Au seuil alpha de 5% choisi au départ avant de faire l’analyse, nous regardons donc si la valeur de p de chaque test est inférieure à ce seuil \(\alpha\) pour rejeter H0 et considérer le coefficient comme significativement différent de zéro. Nous constatons que les droites pour smoke == "before" (décalage d’ordonnée à l’origine \(\beta_1\) et décalage de pente = \(\beta_5\)) sont toutes deux non significatifs. Pour smoke == "during" (décalage d’ordonnée à l’origine \(\beta_3\) et décalage de pente = \(\beta_7\)) nous faisons le même constat. Dans les deux cas, nous concluons donc qu’il n’y a pas de différences avec la droite de référence pour smoke == "never" (pente \(\beta_4\) et ordonnée à l’origine \(\alpha\)). Par contre, tant le décalage de l’ordonnée à l’origine (\(\beta_2\) pour le terme smoke == "until" alias \(smoke_{until}\) dans l’équation) que le décalage de pente (\(\beta_6\) du terme smokeuntil:wt1 alias \(smoke_{until} \times wt1\) dans l’équation) sont significatifs au seuil alpha de 5%. Donc, la sous-population smoke == "until" semble avoir un comportement différent en termes de variation du poids du bébé wt en fonction du poids de la mère wt1 d’après le résumé du modèle linéaire.

Pour vérifier tout cela, nous pouvons considérer le modèle de base comme une droite de régression ajustée entre wt et wt1 pour la sous-population de référence smoke == "never". Ainsi, si nous faisons :

lm(data = babies2, wt ~ wt1, subset = smoke == "never") |>
  summary() |> tabularise()

Modèle linéaire

wt⁡=α+β(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

3.00066

0.12357

24.28

< 2·10-16

***

β\beta_{}

0.00812

0.00207

3.92

9.92·10-05

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.957, 1.499]

Ecart type des résidus : 0.4806 pour 529 degrés de liberté

R2 multiple : 0.02826 - R2 ajusté : 0.02642

Statistique F : 15.38 pour 1 et 529 ddl - valeur de p : 9.9243e-05

Nous voyons en effet que les pentes et ordonnées à l’origine sont ici parfaitement identiques au modèle linéaire complet (mais pas les tests associés). Notez que \(\beta\) dans cette régression simple correspond à \(\beta_4\) dans le modèle de l’ANCOVA.

Faisons de même pour la régression entre wt et wt1 pour la sous-population smoke == "before" :

lm(data = babies2, wt ~ wt1, subset = smoke == "before") |>
  summary() |> tabularise()

Modèle linéaire

wt⁡=α+β(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

2.96516

0.36521

8.12

1.26·10-12

***

β\beta_{}

0.00929

0.00604

1.54

1.27·10-01

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.67, 1.311]

Ecart type des résidus : 0.5231 pour 100 degrés de liberté

R2 multiple : 0.02316 - R2 ajusté : 0.01339

Statistique F : 2.371 pour 1 et 100 ddl - valeur de p : 0.12679

Nous avons une ordonnée à l’origine qui vaut 2,965 et une pente qui vaut 0.00929, exactement comme calculées plus haut (aux arrondis près). L’estimation de l’ordonnée à l’origine correspond donc bien, dans l’ANCOVA, à \(\alpha\) + \(\beta_1\) = 3,000 - -0.0355 = 2,965. De même, la pente de notre droite pour la sous-population smoke == "before" est égale à \(\beta_4\) + \(\beta_5\) = 0.00812 + 0.00118 = 0.00930 (équivalent à 0.00929 aux arrondis près). Cela se vérifie aussi pour les deux autres droites pour smoke == "until" et smoke == "during".

Donc, notre modèle complet ne fait rien d’autre que d’ajuster les quatre droites correspondant aux relations linéaires entre wt et wt1, mais en décompose les effets, niveau par niveau de la variable qualitative smoke en fonction de la matrice de contraste que l’on a choisie. En bonus, nous avons la possibilité de tester si chacune des composantes (tableau coefficient de summary()) ou si globalement chacune des variables (tableau obtenu avec anova()) a un effet significatif ou non dans le modèle.

Le graphique correspondant est le même que si nous avions ajusté les quatre régressions linéaires indépendamment l’une de l’autre (mais les tests et les enveloppes de confiance diffèrent).

chart(data = babies2, wt ~ wt1 %col=% smoke) +
  geom_point() +
  stat_smooth(method = "lm", formula = y ~ x) +
  xlab("wt1 : masse de la mère [kg]") +
  ylab("wt : masse du bébé [kg]")

chart(data = babies2, wt ~ wt1 | smoke) +
  geom_point() +
  stat_smooth(method = "lm", formula = y ~ x) +
  xlab("wt1 : masse de la mère [kg]") +
  ylab("wt : masse du bébé [kg]")

Sur ces deux graphiques, nous voyons très bien que les droites pour smoke == "before" et smoke == "during" sont parallèles à la droite de référence smoke == "never", mais avec un léger décalage qui n’apparaît pas significatif à 5% dans notre analyse, toutefois. Par contre, la droite relative à la sous-population smoke == "until" a une pente très différente ainsi que son ordonnée à l’origine. Et ces différences sont significatives au seuil alpha de 5% (mais ne l’auraient pas été, si nous avions choisi 1% à la place).

Ce résultat est en contradiction avec le tableau de l’ANOVA qui indique que les interactions smoke:wt1 ne sont pas significatives au même seuil \(\alpha\) de 5%. Mais regardez bien les graphiques ci-dessus. Vous constaterez que le positionnement de la droite pour smoke == "until" ne dépend que de quelques cas de mères pesant plus de 80 kg et qui “tirent” la droite vers le bas (idem pour smoke == "before" d’ailleurs, mais ici sans conséquence). De plus, gardez toujours à l’esprit l’intercorrélation des paramètres dans un modèle : si l’un change (la pente), l’autre change aussi (l’ordonnée à l’origine). Que se passe-t-il si nous continuons notre analyse en nous fiant au tableau de l’ANOVA et en excluant donc les interactions du modèle ? Cela veut donc dire que nous considérons même pente pour toutes les droites et que nous autorisons seulement des décalages de l’ordonnée à l’origine entre les sous-populations pour smoke. Il suffit de le faire pour voir ce que cela donne…

# Modèle linéaire sans interactions (+ au lieu de * dans la formule)
babies2_lm2 <- lm(data = babies2, wt ~ smoke + wt1)
summary(babies2_lm2) |> tabularise()

Modèle linéaire

wt⁡=α+β1(smoke⁡before⁡)+β2(smoke⁡until⁡)+β3(smoke⁡during⁡)+β4(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{1}(\operatorname{smoke}_{\operatorname{before}}) + \beta_{2}(\operatorname{smoke}_{\operatorname{until}}) + \beta_{3}(\operatorname{smoke}_{\operatorname{during}}) + \beta_{4}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

3.03005

0.09286

32.630

< 2·10-16

***

β1\beta_{1}

0.03549

0.05407

0.656

5.12·10-01

β2\beta_{2}

0.02267

0.05651

0.401

6.88·10-01

β3\beta_{3}

-0.23794

0.03182

-7.478

1.46·10-13

***

β4\beta_{4}

0.00762

0.00153

4.966

7.85·10-07

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.955, 1.494]

Ecart type des résidus : 0.4999 pour 1185 degrés de liberté

R2 multiple : 0.07733 - R2 ajusté : 0.07422

Statistique F : 24.83 pour 4 et 1185 ddl - valeur de p : < 2.22e-16

anova(babies2_lm2) |> tabularise()
Tableau 3.3:

Terme

Ddl

Somme des carrés

Carrés moyens

Valeur de Fobs.

Valeur de p

smoke

3

18.66

6.22

24.9

1.28·10-15

***

wt1

1

6.16

6.16

24.7

7.85·10-07

***

Résidus

1 185

296.15

0.25

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Maintenant que nous avons éliminé les interactions, nous avons toujours une régression significative entre wt et wt1 (mais avec un R2 toujours très faible de 7,7%), mais maintenant, nous faisons apparaître un effet significatif du contraste avec smoke == "during" au seuil alpha de 5% (\(\beta_3\)). Les effets des deux variables sont également clairs dans notre tableau de l’ANOVA.

À vous de jouer !
h5p

Le graphique correspondant est l’ajustement de droites parallèles les unes aux autres pour les quatre sous-populations en fonction de smoke. Ce graphique est difficile à réaliser. Il faut ruser, et les détails du code vont au-delà de ce cours (il n’est pas nécessaire de les comprendre à ce stade).

offsets <- c(0, 0.03549, 0.02267, -0.23794)
cols <- scales::hue_pal()(4)
chart(data = babies2, wt ~ wt1) +
  geom_point(aes(col = smoke)) +
  purrr::map2(offsets, cols, function(offset, col)
    geom_smooth(method = lm, formula = y + offset ~ x, col = col)) +
  xlab("wt1 : masse de la mère [kg]") +
  ylab("wt : masse du bébé [kg]")

Le graphique montre une tendance claire, comme le tableau du résumé du modèle. Voyons ce que donne l’analyse post hoc des comparaisons multiples.

babies2_lm2_compa <- multcomp::glht(babies2_lm2,
  linfct = multcomp::mcp(smoke = "Tukey")) |> confint()
summary(babies2_lm2_compa)
# 
#    Simultaneous Tests for General Linear Hypotheses
# 
# Multiple Comparisons of Means: Tukey Contrasts
# 
# 
# Fit: lm(formula = wt ~ smoke + wt1, data = babies2)
# 
# Linear Hypotheses:
#                      Estimate Std. Error t value Pr(>|t|)    
# before - never == 0   0.03549    0.05407   0.656    0.908    
# until - never == 0    0.02267    0.05651   0.401    0.977    
# during - never == 0  -0.23794    0.03182  -7.478   <1e-04 ***
# until - before == 0  -0.01282    0.07199  -0.178    0.998    
# during - before == 0 -0.27342    0.05478  -4.991   <1e-04 ***
# during - until == 0  -0.26060    0.05704  -4.568   <1e-04 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# (Adjusted p values reported -- single-step method)
.oma <- par(oma = c(0, 5.1, 0, 0)); plot(babies2_lm2_compa); par(.oma); rm(.oma)

Ici, comme nous testons tous les contrastes, nous pouvons dire que la population des mères qui ont fumé pendant la grossesse smoke == "during" donne des bébés significativement moins gros au seuil \(\alpha\) de 5%, et ce, en comparaison de tous les autres niveaux (mère n’ayant jamais fumé, ou ayant fumé, mais arrêté avant la grossesse, que ce soit longtemps avant ou juste avant). Globalement, le modèle sans interactions donne ici des résultats bien plus clairs que le modèle avec interactions.

Il semble évident maintenant qu’il n’est pas utile de préciser si la mère a fumé ou non avant sa grossesse. L’élément déterminant est uniquement le fait de fumer pendant la grossesse ou non. Nous pouvons le montrer également en utilisant des contrastes de Helmert :

babies2_lm3 <- lm(data = babies2, wt ~ smoke + wt1,
  contrasts = list(smoke = "contr.helmert"))
summary(babies2_lm3) |> tabularise()

Modèle linéaire

wt⁡=α+β1(smoke⁡1⁡)+β2(smoke⁡2⁡)+β3(smoke⁡3⁡)+β4(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{1}(\operatorname{smoke}_{\operatorname{1}}) + \beta_{2}(\operatorname{smoke}_{\operatorname{2}}) + \beta_{3}(\operatorname{smoke}_{\operatorname{3}}) + \beta_{4}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

2.98511

0.09170

32.5547

< 2·10-16

***

β1\beta_{1}

0.01774

0.02703

0.6563

5.12·10-01

β2\beta_{2}

0.00164

0.01960

0.0837

9.33·10-01

β3\beta_{3}

-0.06433

0.00854

-7.5328

9.82·10-14

***

β4\beta_{4}

0.00762

0.00153

4.9656

7.85·10-07

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.955, 1.494]

Ecart type des résidus : 0.4999 pour 1185 degrés de liberté

R2 multiple : 0.07733 - R2 ajusté : 0.07422

Statistique F : 24.83 pour 4 et 1185 ddl - valeur de p : < 2.22e-16

anova(babies2_lm3) |> tabularise()
Tableau 3.4:

Terme

Ddl

Somme des carrés

Carrés moyens

Valeur de Fobs.

Valeur de p

smoke

3

18.66

6.22

24.9

1.28·10-15

***

wt1

1

6.16

6.16

24.7

7.85·10-07

***

Résidus

1 185

296.15

0.25

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Ici les valeurs estimées pour \(\beta_1\), \(\beta_2\) et \(\beta_3\) sont relatives à smoke1 smoke2 et smoke3 qui représentent les trois contrastes utilisés dans la matrice de Helmet (rien à voir avec les niveaux initiaux dans les données brutes babies, attention), soit :

helm <- contr.helmert(4)
rownames(helm) <- c('smoke == "never"', 'smoke == "before"',
                    'smoke == "until"', 'smoke == "during"')
colnames(helm) <- c('smoke1', 'smoke2', 'smoke3')
helm
#                   smoke1 smoke2 smoke3
# smoke == "never"      -1     -1     -1
# smoke == "before"      1     -1     -1
# smoke == "until"       0      2     -1
# smoke == "during"      0      0      3
  • smoke1 est le décalage de l’ordonnée à l’origine entre le modèle moyen établi avec les données smoke == "until" et smoke == "before" et celui pour smoke == "before" (non significatif au seuil alpha de 5%),
  • smoke2 est le décalage de l’ordonnée à l’origine pour smoke == "until" par rapport au modèle ajusté sur smoke == "never", smoke == "before" et smoke == "until" avec des pondérations respectives de -1, -1, et 2 (non significatif au seuil alpha de 5%),
  • smoke3 est le décalage de l’ordonnée à l’origine par rapport au modèle ajusté sur l’ensemble des autres observations et des pondérations respectives comme dans la dernière colonne de la matrice de contraste. Donc, ce dernier contraste est celui qui nous intéresse, car il compare les cas où la mère n’a pas fumé pendant la grossesse avec le cas smoke == "during" où la mère a fumé pendant la grossesse. Ce contraste est significatif au seuil alpha de 5%. L’interprétation des valeurs estimées est plus complexe ici. Comparez ce résultat avec le modèle ajusté avec les contrastes de traitement par défaut :
lm(data = babies2, wt ~ smoke + wt1) |>
  summary() |> tabularise()

Modèle linéaire

wt⁡=α+β1(smoke⁡before⁡)+β2(smoke⁡until⁡)+β3(smoke⁡during⁡)+β4(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{1}(\operatorname{smoke}_{\operatorname{before}}) + \beta_{2}(\operatorname{smoke}_{\operatorname{until}}) + \beta_{3}(\operatorname{smoke}_{\operatorname{during}}) + \beta_{4}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

3.03005

0.09286

32.630

< 2·10-16

***

β1\beta_{1}

0.03549

0.05407

0.656

5.12·10-01

β2\beta_{2}

0.02267

0.05651

0.401

6.88·10-01

β3\beta_{3}

-0.23794

0.03182

-7.478

1.46·10-13

***

β4\beta_{4}

0.00762

0.00153

4.966

7.85·10-07

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.955, 1.494]

Ecart type des résidus : 0.4999 pour 1185 degrés de liberté

R2 multiple : 0.07733 - R2 ajusté : 0.07422

Statistique F : 24.83 pour 4 et 1185 ddl - valeur de p : < 2.22e-16

Les conclusions sont les mêmes, mais les valeurs estimées pour \(\alpha\), \(\beta_1\), \(\beta_2\) et \(\beta_3\) diffèrent. Par exemple, dans ce dernier cas, \(\beta_1\) est estimé au double de la valeur avec les contrastes Helmert, ce qui est logique puisque la référence est ici la droite ajustée pour la sous-population smoke == "never" là où dans le modèle avec les contrastes de Helmert, le décalage est mesuré par rapport au modèle moyen (donc à “mi-chemin” entre les deux droites pour smoke == "never" et smoke == "before").

Naturellement, nous pouvons aussi considérer la variable smoke comme une variable facteur ordonnée (ordered). Dans ce cas, c’est les contrastes polynomiaux qui sont utilisés :

smutate(babies2, smoke = as.ordered(smoke)) |>
  lm(data = _, wt ~ smoke + wt1) |>
  summary() |>
  tabularise()

Modèle linéaire

wt⁡=α+β1(smoke⁡.L⁡)+β2(smoke⁡.Q⁡)+β3(smoke⁡.C⁡)+β4(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{1}(\operatorname{smoke}_{\operatorname{.L}}) + \beta_{2}(\operatorname{smoke}_{\operatorname{.Q}}) + \beta_{3}(\operatorname{smoke}_{\operatorname{.C}}) + \beta_{4}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

2.98511

0.09170

32.555

< 2·10-16

***

β1\beta_{1}

-0.16248

0.02678

-6.067

1.75·10-09

***

β2\beta_{2}

-0.14804

0.03929

-3.768

1.73·10-04

***

β3\beta_{3}

-0.04460

0.04879

-0.914

3.61·10-01

β4\beta_{4}

0.00762

0.00153

4.966

7.85·10-07

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.955, 1.494]

Ecart type des résidus : 0.4999 pour 1185 degrés de liberté

R2 multiple : 0.07733 - R2 ajusté : 0.07422

Statistique F : 24.83 pour 4 et 1185 ddl - valeur de p : < 2.22e-16

Notez que R est capable d’utiliser automatiquement les contrastes adéquats (polynomiaux) lorsque la variable facteur smoke est encodée en ordered. Des contrastes tenant compte d’une variation le long des successions croissantes de niveaux de “gravité” de la variable smoke sont maintenant calculés, ce qui donne des résultats (et une équation) encore différents. Le coefficient \(\beta_1\) relatif à smoke.L indique une variation linéaire (significative au seuil alpha de 5%). Le coefficient \(\beta_2\) du terme smoke.Q est une variation quadratique (également significative) et enfin \(\beta_3\) du terme smoke.C pour une variation cubique, lui, ne l’est pas. Voyez la présentation des matrices de contrastes plus haut pour bien comprendre ce qui est calculé ici.

Au final, il apparaît que l’élément important relatif à la variable smoke est en définitive le fait de fumer pendant la grossesse ou non, pas l’histoire de la mère avant sa grossesse par rapport à la cigarette ! En modélisation, nous avons toujours intérêt à choisir le modèle le plus simple. Donc ici, cela vaut le coup de simplifier smoke à une variable à deux niveaux smokepreg qui indique uniquement si la mère fume ou non pendant la grossesse. Ensuite, nous ajustons à nouveau un modèle plus simple avec cette nouvelle variable.

babies2 %>.%
  smutate(., smokepreg = recode(smoke, "never" = "0", "before" = "0",
                                       "until" = "0", "during" = "1")) %>.%
  smutate(., smokepreg = factor(smokepreg, levels = c("0", "1"))) ->
  babies2
babies2_lm4 <- lm(data = babies2, wt ~ smokepreg + wt1)
summary(babies2_lm4) |> tabularise()

Modèle linéaire

wt⁡=α+β1(smokepreg⁡1⁡)+β2(wt1⁡)+ϵ\operatorname{wt} = \alpha + \beta_{1}(\operatorname{smokepreg}_{\operatorname{1}}) + \beta_{2}(\operatorname{wt1}) + \epsilon

Terme

Valeur estimée

Ecart type

Valeur de t

Valeur de p

α\alpha

3.03751

0.09190

33.05

< 2·10-16

***

β1\beta_{1}

-0.24580

0.02975

-8.26

3.76·10-16

***

β2\beta_{2}

0.00762

0.00153

4.98

7.25·10-07

***

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Etendue des résidus : [-1.962, 1.487]

Ecart type des résidus : 0.4996 pour 1187 degrés de liberté

R2 multiple : 0.07692 - R2 ajusté : 0.07537

Statistique F : 49.46 pour 2 et 1187 ddl - valeur de p : < 2.22e-16

anova(babies2_lm4) |> tabularise()
Tableau 3.5:

Terme

Ddl

Somme des carrés

Carrés moyens

Valeur de Fobs.

Valeur de p

smokepreg

1

18.50

18.50

74.1

< 2·10-16

***

wt1

1

6.19

6.19

24.8

7.25·10-07

***

Résidus

1 187

296.28

0.25

0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

À présent, tous les termes de notre modèle sont significatifs au seuil \(\alpha\) de 5%. Le coefficient \(\beta_1\) du terme \(smokepreg_1\) est le décalage de l’ordonnée à l’origine du poids des bébés issus de mères fumant pendant la grossesse. Il donne donc directement la perte moyenne de poids des bébés lié aux femmes qui fument pendant la grossesse par rapport à celles qui ne fument pas à ce moment-là. La représentation graphique de ce dernier modèle est la suivante :

offsets <- c(0, -0.2458)
cols <- scales::hue_pal()(2)
chart(data = babies2, wt ~ wt1) +
  geom_point(aes(col = smokepreg)) +
  purrr::map2(offsets, cols, function(offset, col)
    geom_smooth(method = lm, formula = y + offset ~ x, col = col)) +
  xlab("wt1 : masse de la mère [kg]") +
  ylab("wt : masse du bébé [kg]")

Enfin, n’oublions pas que notre modèle n’est valide que si les conditions d’application sont rencontrées, en particulier, une distribution Normale des résidus et une homoscédasticité (même variance pour les résidus). Nous vérifions cela visuellement toujours avec les graphiques d’analyse des résidus. En voici les plus importants :

chart$resfitted(babies2_lm4)

chart$qqplot(babies2_lm4)

chart$scalelocation(babies2_lm4)

chart$cooksd(babies2_lm4)

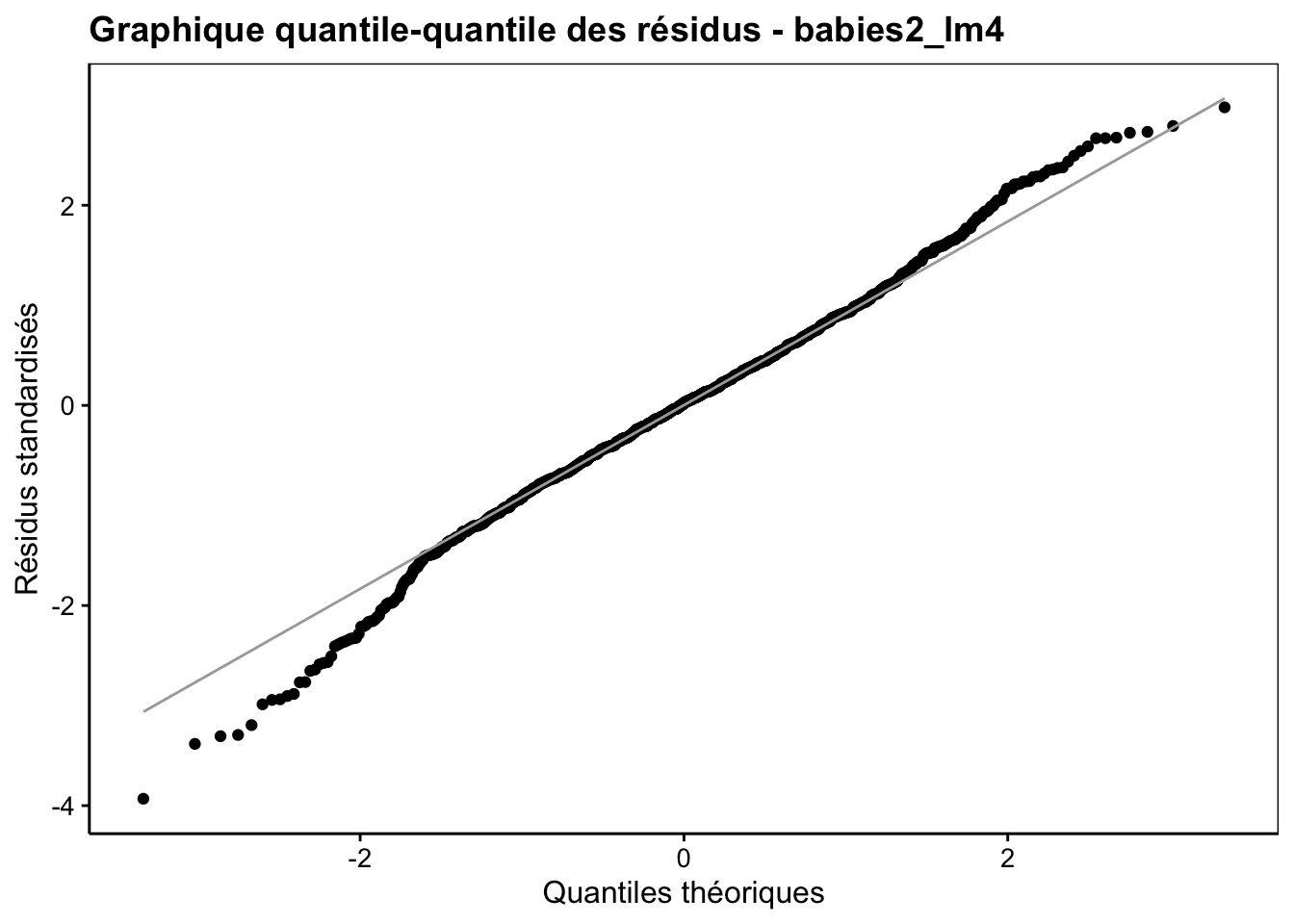
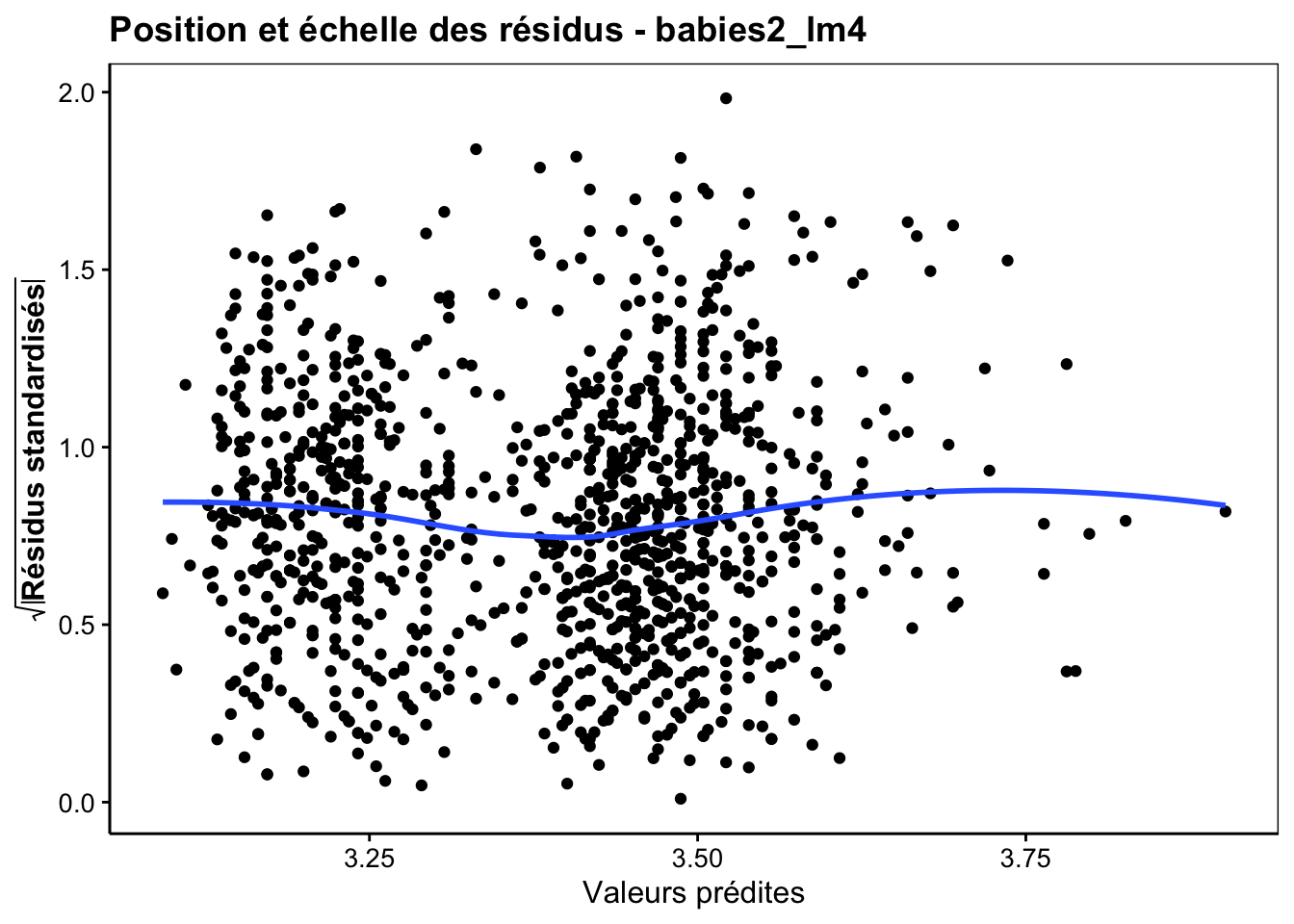
Ici le comportement des résidus est sain. Des petits écarts à la normalité sur le graphique quantile-quantile s’observent peut-être, mais ce n’est pas dramatique et le modèle linéaire est robuste à ce genre de petits changements d’autant plus qu’ils apparaissent relativement symétriques à gauche et à droite de la distribution. En conclusion de cette analyse, nous pouvons dire que la masse du bébé dépend de la masse de la mère, mais assez faiblement (seulement 7,7% de la variance totale expliquée). Par contre, nous pouvons aussi dire que le fait de fumer pendant la grossesse a un effet moyen significatif sur la réduction de la masse du bébé à la naissance (en moyenne cette réduction est de 0,25kg pour une masse moyenne à la naissance de 3,04kg, soit une réduction de 0,25 / 3,04 * 100 = 8%).

Voilà, nous venons d’analyser et d’interpréter notre premier modèle linéaire constitué d’une variable prédictive numérique et d’une variable prédictive facteur (anciennement appelé ANCOVA). Les données à traiter (graphiques descriptifs) ne montraient a priori pas un allongement visible du nuage de point, et effectivement, le R2 du modèle est extrêmement faible (< 8%). Il n’est pas utilisable pour prédire la masse du bébé à la naissance en fonction de la masse de la mère, bien que la relation soit significative au seuil \(\alpha\) de 5%. Il nous a pourtant servis à mettre en évidence un léger décalage significatif de la masse du bébé pour des mères qui ont fumé pendant leur grossesses. Ceci n’aurait pas été mis en évidence par une ANOVA à un facteur sans tenir compte de la relation masse du bébé versus masse de la mère simultanément dans le modèle linéaire. En pratique, la plupart des données que vous traiterez en modèle linéaire (ou ANCOVA) auront très probablement un bien meilleur R2. Mais ce jeu de données a été choisi pour vous montrer qu’il est parfois possible de sortir des résultats intéressants de données pour lesquelles une première analyse descriptive ne montre pas de relation évidente.

3.4.3 Choix du modèle

Un modèle linéaire constitué d’une variable dépendante numérique (Y) et de deux variables explicatives dont l’une est numérique (X) et l’autre qualitative (variable “factor” F), peut s’écrire de plusieurs façons différentes. Graphiquement, il s’agit d’ajuster des droites entre X et Y qui diffèrent d’un niveau à l’autre de la variable F. Considérant que le facteur F est fixe et que les observations sont indépendantes les unes des autres, nous avons essentiellement trois cas de figure (ici, une situation fictive où F n’a que deux modalités ou niveaux nommés “A” et “B”) :

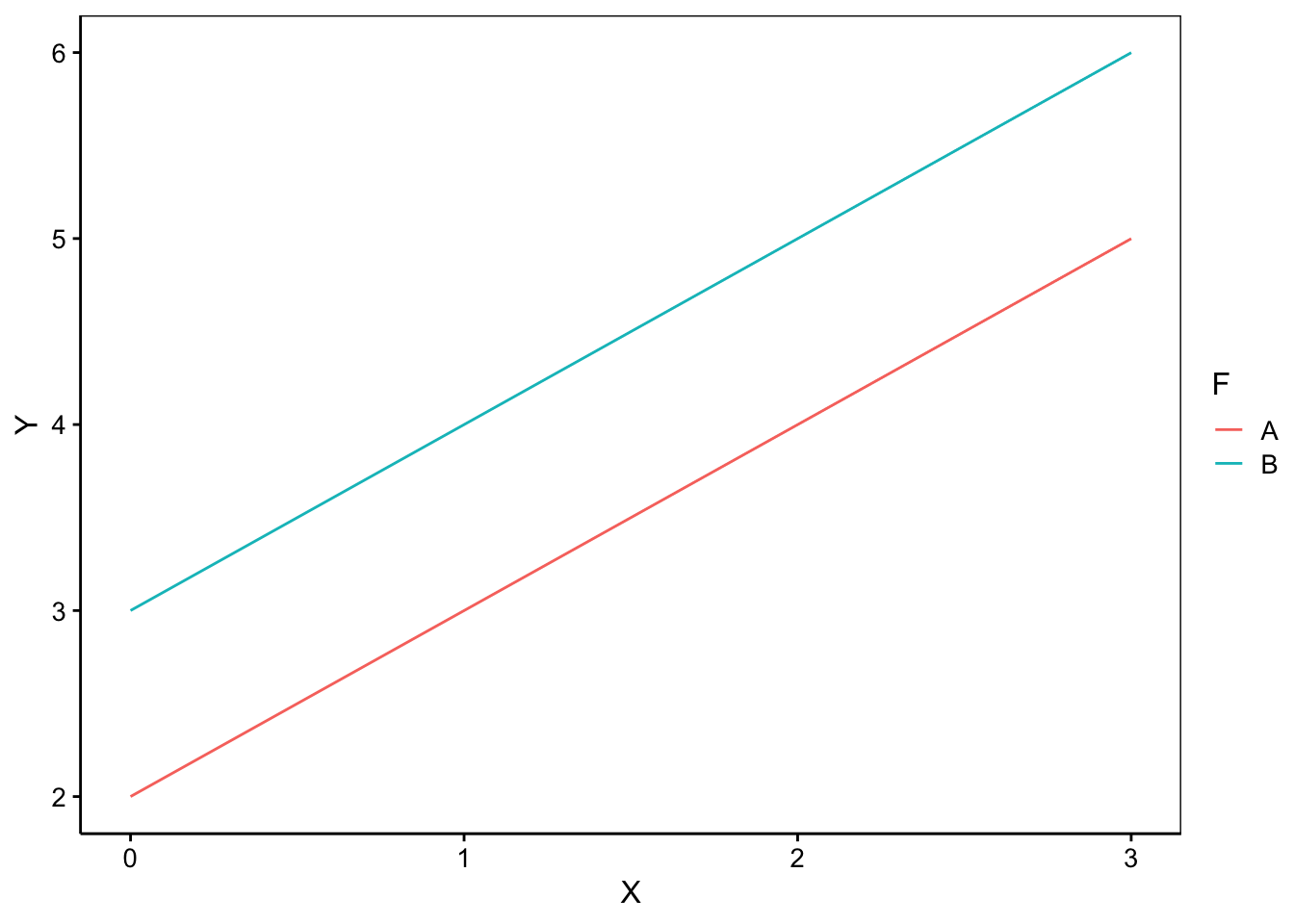
  • Les deux nuages de points sont parallèles l’un à l’autre. Les deux droites diffèrent donc seulement par un décalage de l’ordonnée à l’origine. La formule à considérer dans R est alors Y ~ X + F.

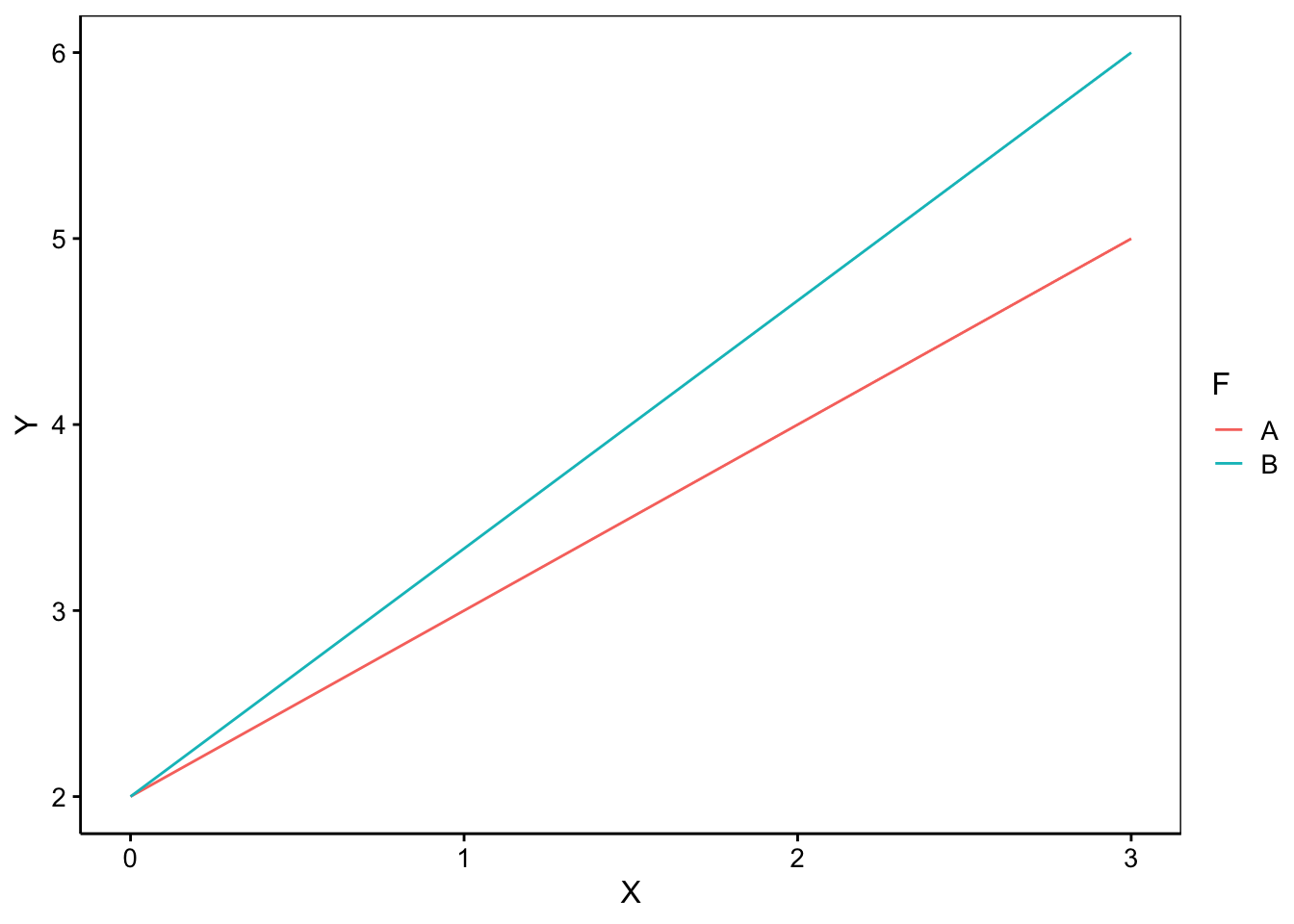
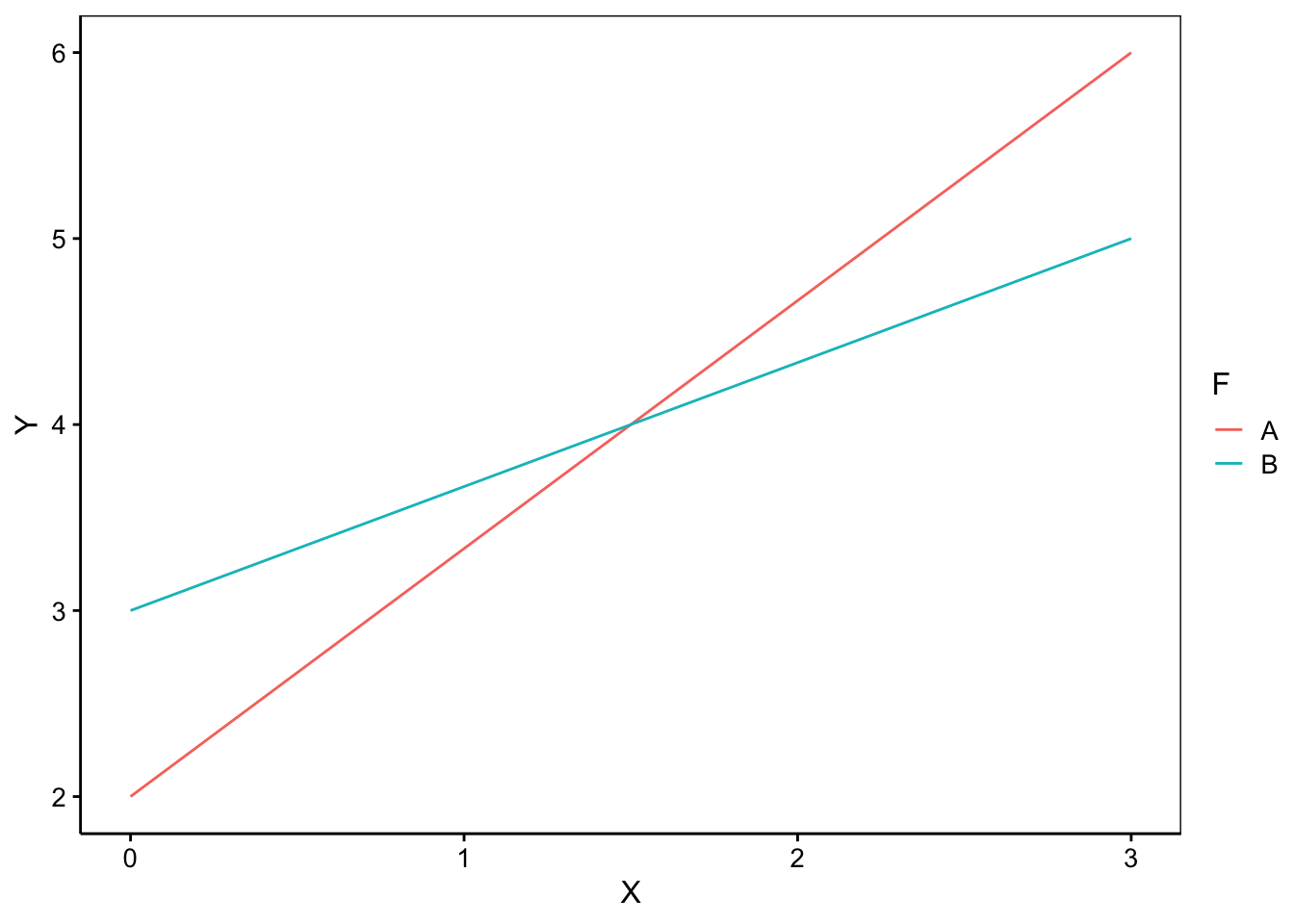
  • Les deux nuages de points s’allongent linéairement le long de droites ayant des pentes différentes, mais qui se croisent en X = 0. Les droites diffèrent donc par leurs pentes, mais pas par leurs ordonnées à l’origine. Cela s’exprime par des interactions entre X et F dans le modèle qui se notent X:F dans une formule. Nous écrirons donc notre modèle comme Y = X + X:F.

  • Les deux droites se croisent en un point quelconque différent de X = 0. Les droites diffèrent à la fois par leurs pentes et par leurs ordonnées à l’origine. Le modèle complet sera alors utilisé. Dans R nous écrirons : Y = X + F + X:F. Une forme abrégée synonyme existe aussi : Y = X * F. Ces deux formules décrivent strictement le même modèle et sont interchangeables.

En pratique, et surtout en cas de doute, vous pouvez commencer par ajuster le modèle complet. Ensuite vous analysez les différentes lignes du tableau issu de summary() appliqué à votre modèle. Vous déterminer si le test t de Student qui est réalisé sur chaque paramètre du modèle (H0: le paramètre vaut zéro, H1: le paramètre est différent de zéro) rejette l’hypothèse nulle de manière significative au seuil alpha choisi. Si pas, cela signifie que ce paramètre peut probablement être ignoré dans le modèle (c’est-à-dire, forcé à zéro dans l’équation) et vous pouvez alors passer sur une forme plus concise, soit le modèle sans interactions à droites parallèles, soit le modèle avec uniquement les interactions pour des droites qui se croisent à l’origine de l’axe des abscisses.

À vous de jouer !

Effectuez maintenant les exercices du tutoriel B03La_mod_lin (Modèle linéaire).

BioDataScience2::run("B03La_mod_lin")

Le projet suivant est individuel et cadré.

Réalisez le travail B03Ia_who.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q1 : modélisation) à terminer avant le 2023-11-13 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md.

Références

Verzani, John. 2005. Using r for Introductory Statistics. Boca Raton, Florida: Chapman; Hall/CRC. https://www.crcpress.com/Using-R-for-Introductory-Statistics/Verzani/p/book/9781466590731.

  1. Pour rappel, on utilise le signe + pour indiquer un modèle sans interactions et un signe * pour spécifier un modèle complet avec interactions entre les variables.↩︎