2.2 Régression linéaire multiple

Dans le cas de la régression linéaire simple, nous considérions le modèle statistique suivant (avec \(\epsilon\) représentant les résidus, terme statistique dans l’équation) :

\[y = \alpha + \beta \ x + \epsilon \]

Dans le cas de la régression linéaire multiple, nous introduisons plusieurs variables indépendantes notées \(x_1\), \(x_2\), …, \(x_n\) :

\[y = \alpha + \beta_1 \ x_1 + \beta_2 \ x_2 + ... + \beta_n \ x_n + \epsilon \]

La bonne nouvelle, c’est que tous les calculs, les métriques et les tests d’hypothèses relatifs à la régression linéaire simple se généralisent, tout comme nous sommes passés dans le cours SDD 1 de l’ANOVA à un facteur à un modèle plus complexe à deux ou plusieurs facteurs. Voyons tout de suite ce que cela donne si nous utilisons à la fois le diamètre et la hauteur des cerisiers noirs pour prédire leur volume de bois :

trees_lm3 <- lm(data = trees, volume ~ diameter + height)
summary(trees_lm3) |>
  tabularise()

Modèle linéaire
$\operatorname{Volume\ de\ bois \ [m^{3}]} = \alpha + \beta_{1}(\operatorname{Diamètre\ à\ 1,4m \ [m]}) + \beta_{2}(\operatorname{Hauteur \ [m]}) + \epsilon$
Terme	Valeur estimée	Ecart type	Valeur de t	Valeur de p
$\alpha$	-1.6356	0.2446	-6.69	2.95·10-07	***
$\beta_{1}$	5.2564	0.2959	17.76	< 2·10-16	***
$\beta_{2}$	0.0311	0.0121	2.57	1.56·10-02	*
0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05
Etendue des résidus : [-0.1804, 0.2418]
Ecart type des résidus : 0.1104 pour 28 degrés de liberté
R2 multiple : 0.9475 - R2 ajusté : 0.9438
Statistique F : 252.7 pour 2 et 28 ddl - valeur de p : < 2.22e-16

D’un point de vue pratique, nous voyons que la formule qui spécifie le modèle peut très bien comporter plusieurs variables séparées par des +. Nous avons ici trois paramètres dans notre modèle : l’ordonnée à l’origine \(\alpha\) qui vaut -1,64, la pente relative au diamètre \(\beta_1\) de 5,26, et la pente relative à la hauteur \(\beta_2\) de 0,031. Le modèle trees_lm3 sera donc paramétré comme suit : volume de bois = 5,26 . diamètre + 0,031 . hauteur - 1,64… mais nous pouvons tout aussi bien laisser la fonction eq__() extraire cette équation paramétrée pour nous, en précisant l’argument use_coefs = TRUE) (ici, nous avons aussi ajouté coef_digits = c(2, 2, 3) pour avoir deux chiffres derrière la virgule pour les premiers paramètres et trois pour le dernier) :

\[\operatorname{\widehat{Volume\ de\ bois \ [m^{3}]}} = -1.64 + 5.26(\operatorname{Diamètre\ à\ 1,4m \ [m]}) + 0.031(\operatorname{Hauteur \ [m]})\]

Notons que la pente relative à la hauteur (0,031) n’est pas significativement différente de zéro au seuil \(\alpha\) de 1% (mais l’est seulement pour \(\alpha\) = 5%). En effet, la valeur t du test de Student pour \(\beta_2\) (rappel : H₀ : le paramètre vaut zéro, H₁ : le paramètre est différent de zéro) vaut 2,57. Cela correspond à une valeur p du test de 0,0156, une valeur moyennement significative donc, matérialisée par un seul astérisque à la droite du tableau. Cela dénote un plus faible pouvoir de prédiction du volume de bois par la hauteur que par le diamètre de l’arbre. Nous l’avions déjà observé sur le graphique matrice de nuages de points réalisé initialement, ainsi que par l’intermédiaire des coefficients de corrélation respectifs.

La représentation de cette régression nécessite un graphique à trois dimensions (diamètre, hauteur et volume) et le modèle représente en fait le meilleur plan dans cet espace à trois dimensions. Pour un modèle comportant plus de deux variables indépendantes, il n’est plus possible de représenter graphiquement la régression.

library(rgl)

# Warning in rgl.init(initValue, onlyNULL): RGL: unable to open X11 display

# Warning: 'rgl.init' failed, running with 'rgl.useNULL = TRUE'.

knitr::knit_hooks$set(webgl = hook_webgl)

car::scatter3d(data = trees, volume ~ diameter + height,
  fit = "linear", residuals = TRUE, bg = "white", axis.scales = TRUE,
  grid = TRUE, ellipsoid = FALSE)
rgl::rglwidget(width = 800, height = 800)

Utilisez la souris pour zoomer (molette) et pour retourner le graphique (cliquez et déplacez la souris en maintenant le bouton enfoncé) pour comprendre ce graphique 3D. La régression est matérialisée par un plan bleu. Les observations sont les boules jaunes et les résidus sont des traits cyan lorsqu’ils sont positifs et magenta lorsqu’ils sont négatifs.

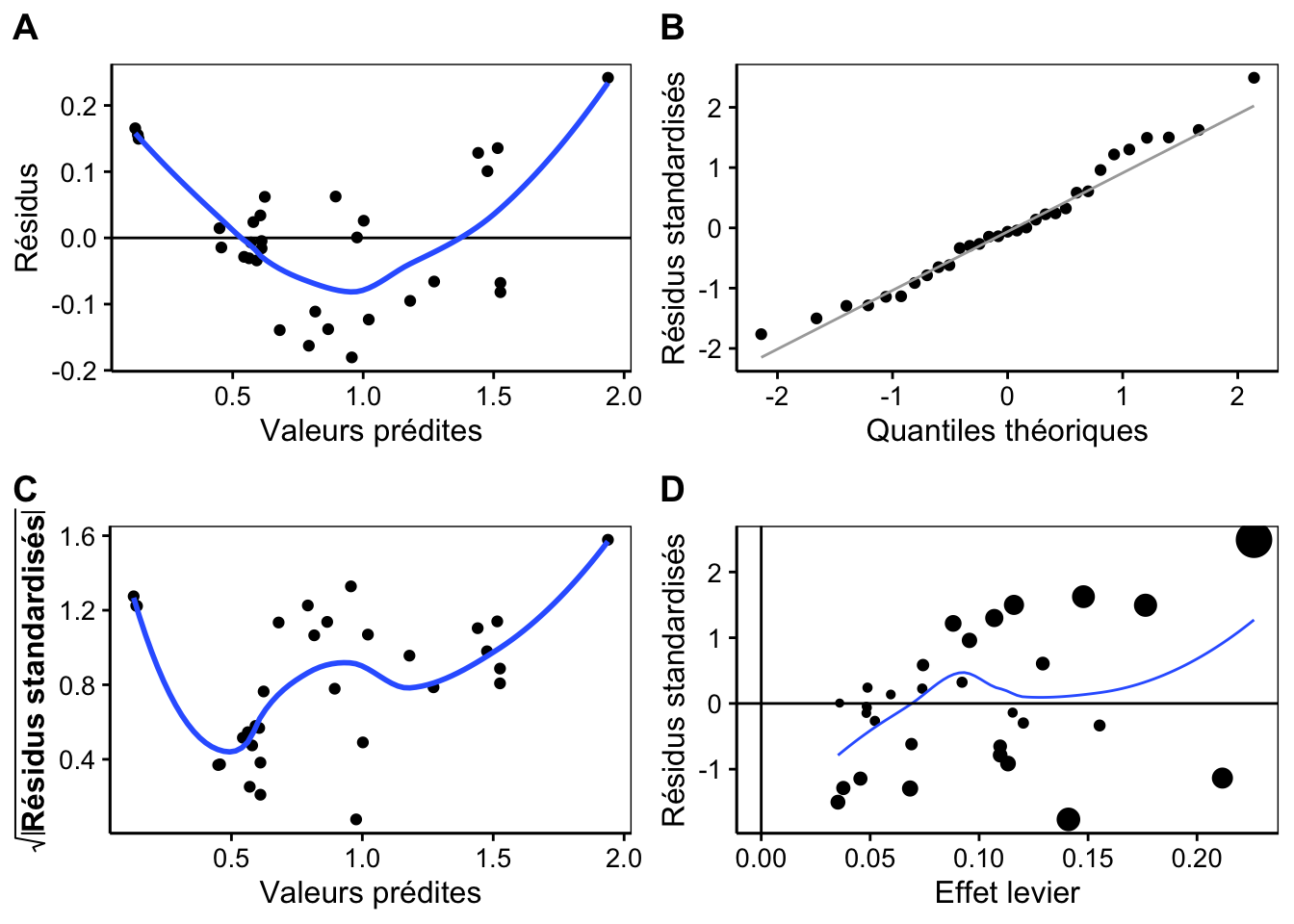
Les graphes d’analyse des résidus sont toujours disponibles :

chart$residuals(trees_lm3) 

À vous de jouer !

Ce modèle est-il préférable à celui n’utilisant que le diamètre ? Le R² ajusté est passé de 0,93 avec le modèle simple trees_lm utilisant uniquement le diamètre à 0,94 dans le présent modèle trees_lm3 utilisant le diamètre et la hauteur. Cela semble une amélioration, mais le test de significativité de la pente pour la hauteur ne nous indique pas un résultat hautement significatif. De plus, cela a un coût en pratique de devoir mesurer deux variables au lieu d’une seule pour estimer le volume de bois. Cela en vaut-il la peine ? Nous sommes encore une fois confrontés à la question de comparer deux modèles, cette fois-ci ayant une complexité différente (comprenez, un nombre de paramètres à estimer différent).

À vous de jouer !

Dans le cas particulier de modèles imbriqués (un modèle contient l’autre, mais rajoute un ou plusieurs termes), une ANOVA est possible en décomposant la variance selon les composantes reprises respectivement par chacun des deux modèles. La fonction anova() est programmée pour faire ce calcul en lui indiquant chacun des deux objets contenant les modèles à comparer :

anova(trees_lm, trees_lm3) |>
  tabularise()

Analyse de la variance Modèle 1: volume ~ diameter Modèle 2: volume ~ diameter + height
Modèle	Ddl des résidus	Somme des carrés des résidus	Ddl	Somme des carrés	Valeur de Fobs.	Valeur de p
Modèle 1	29	0.422
Modèle 2	28	0.341	1	0.0807	6.63	0.0156	*
0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05

Notez que dans le cas de l’ajout d’un seul terme, la valeur p de cette ANOVA est identique à la valeur p de test de significativité du paramètre de ce nouveau terme (ici, cette valeur p est de 0,0156 dans les deux cas). Donc, le choix peut se faire directement à partir de summary() pour ce terme unique. La conclusion est similaire : l’ANOVA donne un résultat seulement moyennement significatif entre les deux modèles. Dans un cas plus complexe, la fonction anova() de comparaison pourra être utile. Enfin, tous les modèles ne sont pas nécessairement imbriqués. Dans ce cas, il nous faudra un autre moyen de les départager… mais avant d’aborder cela, étudions une variante intéressante de la régression multiple : la régression polynomiale.

À vous de jouer !

Effectuez maintenant les exercices du tutoriel B02La_reg_multi (Régression linéaire multiple).

BioDataScience2::run("B02La_reg_multi")