5.2 Types de variables
Lors de la réalisation de graphiques dans les modules précédents vous avez compris que toutes les variables ne sont pas équivalentes. Certains graphiques sont plutôt destinés à des variables qualitatives (par exemple, graphique en barres), alors que d’autres représentent des données quantitatives comme le nuage de points.
# # A tibble: 395 x 7
# gender day_birth weight height wrist year_measure age
# <fct> <date> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 M 1995-03-11 69 182 15 2013 18
# 2 M 1998-04-03 74 190 16 2013 15
# 3 M 1967-04-04 83 185 17.5 2013 46
# 4 M 1994-02-10 60 175 15 2013 19
# 5 W 1990-12-02 48 167 14 2013 23
# 6 W 1994-07-15 52 179 14 2013 19
# 7 W 1971-03-03 72 167 15.5 2013 42
# 8 W 1997-06-24 74 180 16 2013 16
# 9 M 1972-10-26 110 189 19 2013 41
# 10 M 1945-03-15 82 160 18 2013 68
# # … with 385 more rowsLa Figure 5.1 montre deux boites de dispersion parallèles différentes. Laquelle de ces deux représentations est incorrecte et pourquoi ?
a <- chart(biometry, height ~ gender %fill=% gender) +
geom_boxplot()
b <- chart(biometry, height ~ weight %fill=% gender) +
geom_boxplot()
combine_charts(list(a, b), common.legend = TRUE)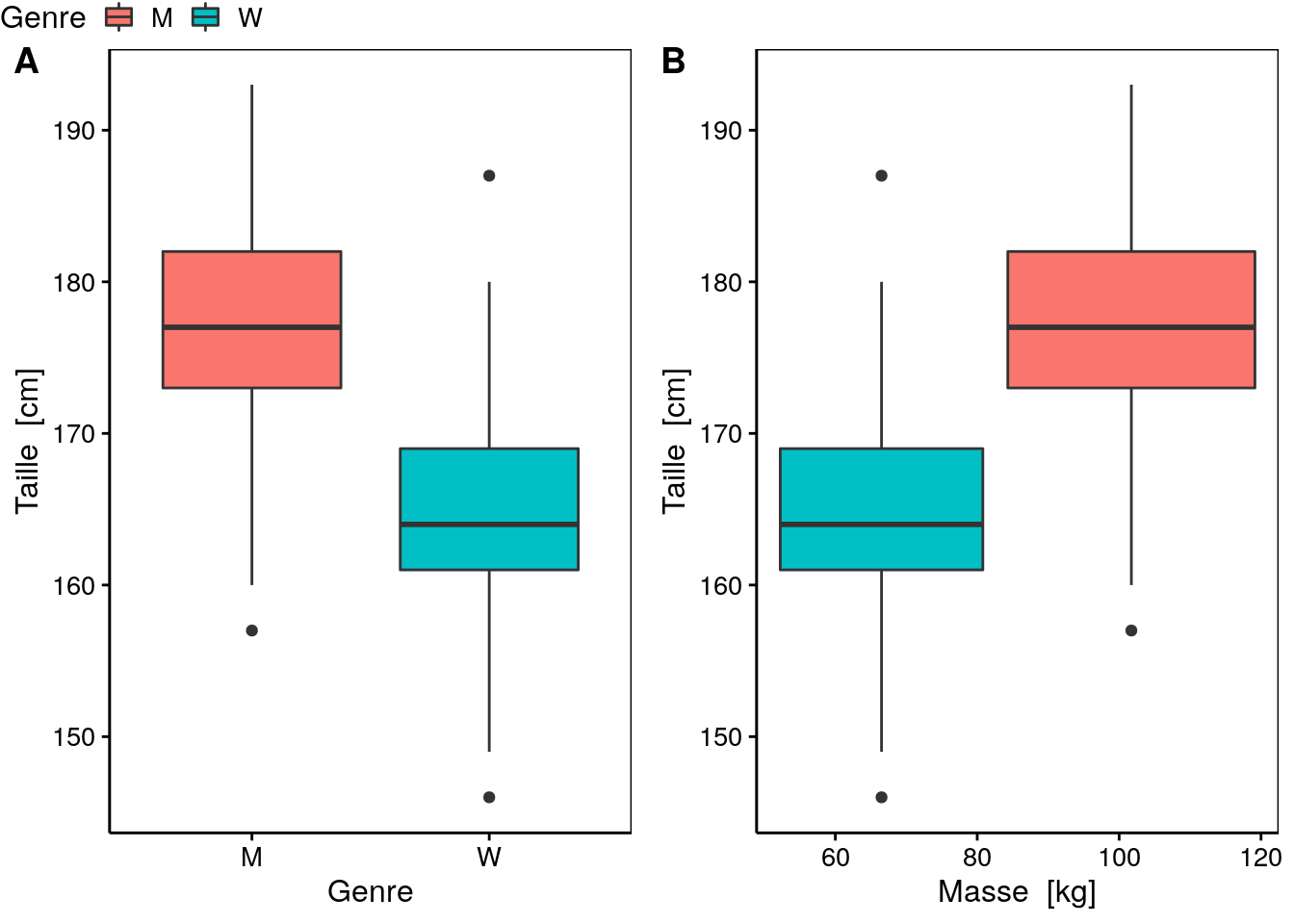
Figure 5.1: Boites de dispersion parallèles de la taille (height) en fonction de A. une variable qualitative (gender) et B. une variable quantitative (weight) et couleur en fonction de gender`
C’est la Figure 5.1B qui tente de représenter une variable quantitative numérique heightsous forme de boites de dispersion parallèles (correct), mais en fonction d’une variable de découpage en sous-ensemble (weight) qui est elle-même une variable quantitative, … alors qu’une variable qualitative telle que gender aurait dû être utilisée (comme dans la Fig. 5.1A). Dans le cas présent, R a bien voulu réaliser le graphique (avec juste un petit message d’avertissement), mais comment l’interpréter ? Dans d’autres situations, il vous renverra purement et simplement un message d’erreur.
Les jeux de données, lorsqu’ils sont bien encodés (tableaux “cas par variables”, en anglais on parlera de tidy data), sont en fait un ensemble de variables en colonnes mesurées sur un ensemble d’individus en lignes. Vous avez à votre disposition plusieurs types de variables pour personnaliser le jeu de données. Deux catégories principales de variables existent, chacune avec deux sous-catégories :
- Les variables quantitatives sont issues de mesures quantitatives ou de dénombrements
- Les variables quantitatives continues sont représentées par des valeurs réelles (
doubledans R) - Les variables quantitatives discrètes sont typiquement représentées par des entiers (
integerdans R)
- Les variables quantitatives continues sont représentées par des valeurs réelles (
- Les variables qualitatives sont constituées d’un petit nombre de valeurs possibles (on parle des niveaux de la variables ou de leurs modalités)
- Les variables qualitatives ordonnées ont des niveaux qui peuvent être classés dans un ordre du plus petit au plus grand. elles sont typiquement représentées dans R par des objets
ordered. - Les variables qualitatives non ordonnées ont des niveaux qui ne peuvent être rangés et sont typiquement représentées par des objets
factoren R
- Les variables qualitatives ordonnées ont des niveaux qui peuvent être classés dans un ordre du plus petit au plus grand. elles sont typiquement représentées dans R par des objets
Il existe naturellement encore d’autres types de variables. Les dates sont représentées, par exemple, par des objets Date, les nombres complexes par complex, les données binaires par raw, etc.
La fonction skim() du package {skimr} permet de visualiser la classe de la variable et bien plus encore. Elle fournit un résumé différent en fonction du type de la variable et propose, par exemple, un histogramme stylisé pour les variables numériques comme le montre le tableau ci-dessous.
| Name | biometry |
| Number of rows | 395 |
| Number of columns | 7 |
| _______________________ | |
| Column type frequency: | |
| Date | 1 |
| factor | 1 |
| numeric | 5 |
| ________________________ | |
| Group variables | None |
Variable type: Date
| skim_variable | n_missing | complete_rate | min | max | median | n_unique |
|---|---|---|---|---|---|---|
| day_birth | 0 | 1 | 1927-08-29 | 2000-08-11 | 1988-10-05 | 210 |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| gender | 0 | 1 | FALSE | 2 | M: 198, W: 197 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| weight | 0 | 1.00 | 71.20 | 15.45 | 41.5 | 59.0 | 69.3 | 80 | 131 | ▅▇▅▁▁ |
| height | 0 | 1.00 | 170.71 | 9.07 | 146.0 | 164.0 | 171.0 | 177 | 193 | ▁▆▇▆▂ |
| wrist | 2 | 0.99 | 16.65 | 1.67 | 10.0 | 15.5 | 16.5 | 18 | 23 | ▁▃▇▃▁ |
| year_measure | 0 | 1.00 | 2015.32 | 1.61 | 2013.0 | 2014.0 | 2016.0 | 2017 | 2017 | ▅▅▁▅▇ |
| age | 0 | 1.00 | 35.34 | 17.32 | 15.0 | 19.0 | 27.0 | 50 | 89 | ▇▁▅▁▁ |
Avec une seule instruction, on obtient une quantité d’information sur notre jeu de données comme le nombre d’observations, le nombre de variables et un traitement spécifique pour chaque type de variable. Cette instruction permet de visualiser et d’appréhender le jeu de données mais ne doit généralement pas figurer tel quel dans un rapport d’analyse.