2.1 Nuage de points

Dès que vous vous sentez familiarisé avec les principes de base de R, vous allez pouvoir réaliser assez rapidement des beaux graphiques. Par exemple, si vous souhaitez représenter une variable numérique en fonction d’une autre variable numérique, vous pouvez exprimer cela sous la forme d’une formule3

\[y \sim x\]

que l’on peut lire “y en fonction de x”. Pour les deux variables numériques x et y, la représentation graphique la plus classique est le nuage de points (voir Fig. 2.1 pour un exemple).

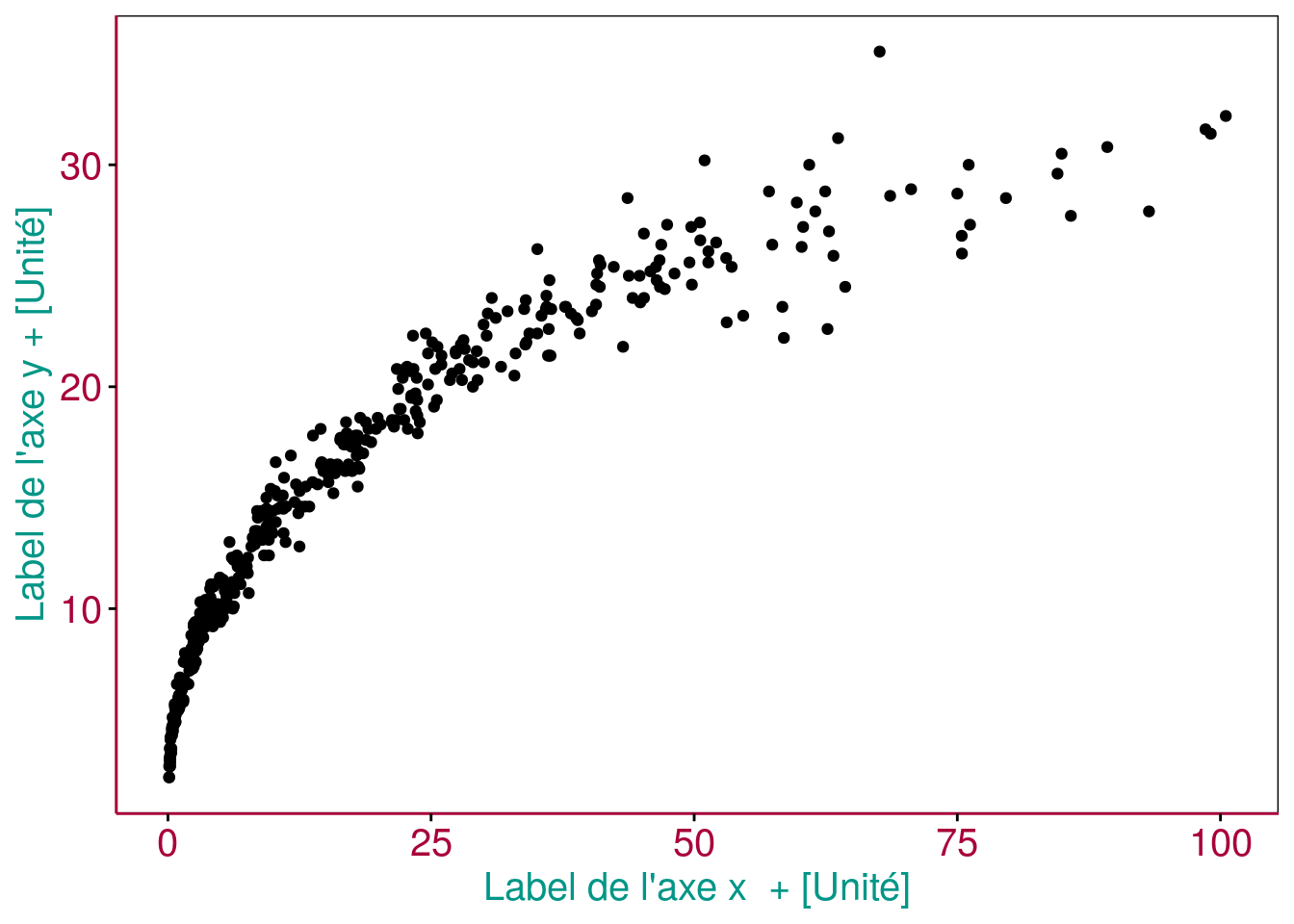
Exemple de graphique en nuage de points. Des éléments essentiels sont ici mis en évidence en couleurs (voir texte). \label{np_intro}

Figure 2.1: Exemple de graphique en nuage de points. Des éléments essentiels sont ici mis en évidence en couleurs (voir texte).

Les éléments indispensables à la compréhension d’un graphique en nuage de points sont mis en évidence à la Fig. 2.1 :

  • Les axes avec les graduations (en rouge),
  • les labels et les unités des axes (en bleu).

Les instructions dans R pour produire un tel nuage de points sont :

# Chargement de SciViews::R
SciViews::R
# Importation du jeu de données
urchin <- read("urchin_bio", package = "data.io", lang = "fr")
# Visualisation interactive du tableau de données

DT::datatable(urchin , filter = 'top', class = "cell-border compact", 
  rownames = FALSE, options = list(pageLength = 5, scrollX = TRUE),
  caption = "Jeu de données sur la biométrie des oursins")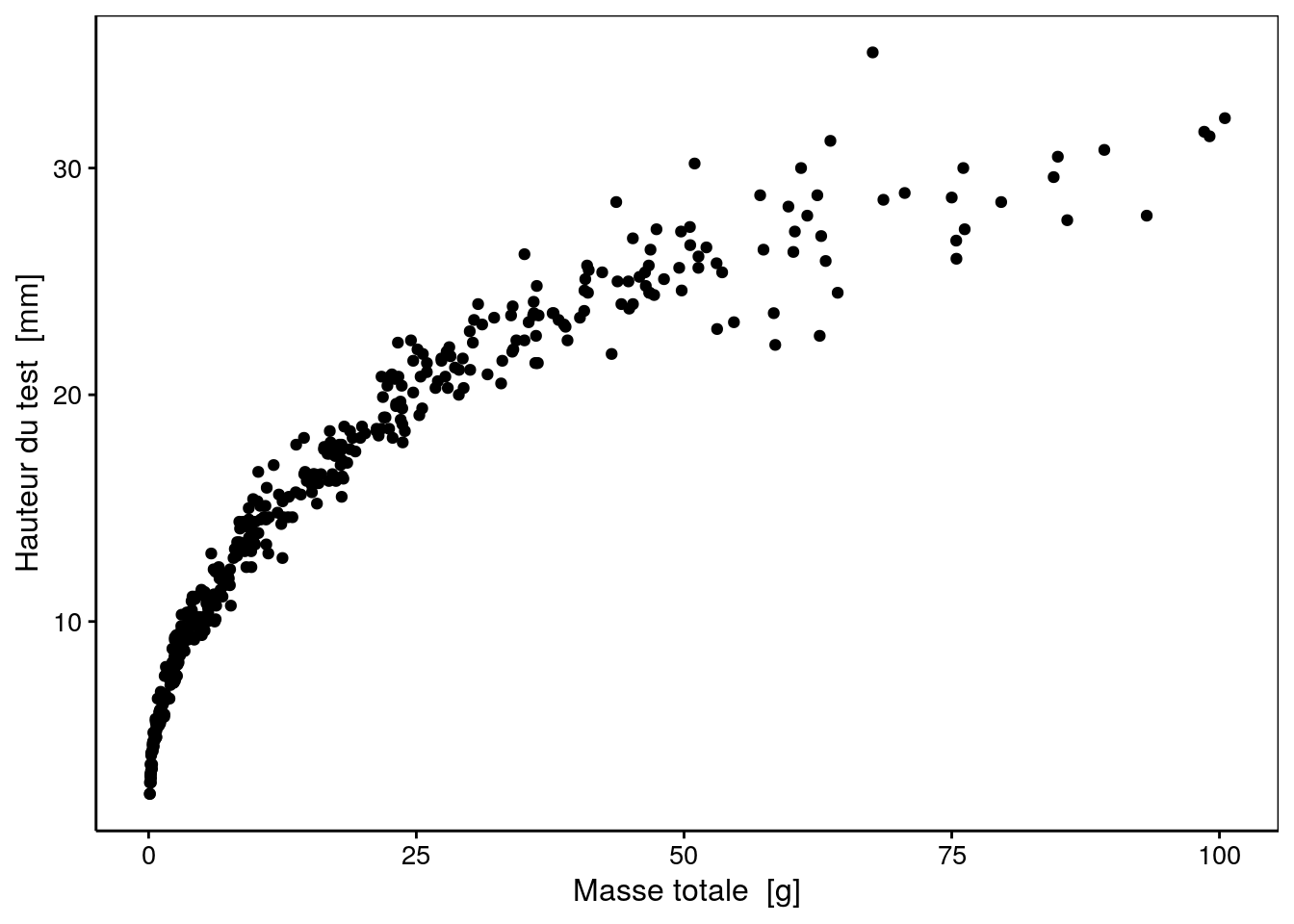
# Réalisation du graphique 
chart(data = urchin, height ~ weight) +
  geom_point()
Taille (hauteur du test) d'oursins en fonction de leur masse.

Figure 2.2: Taille (hauteur du test) d’oursins en fonction de leur masse.

La fonction chart() n’est pas accessible dans R de base, mais l’extension chargée via l’instruction SciViews::R rend cette fonction disponible. Elle requiert comme argument le jeu de donnée (data = urchin, c’est un objet dataframe ou tibble dans le langage de R), ainsi que la formule à employer dans laquelle vous avez indiqué le nom des variables que vous voulez sur l’axe des ordonnées à gauche et des abscisses à droite de la formule, les deux membres étant séparés par un “tilde” (~). Vous voyez que le jeu de données contient beaucoup de variables (les titres des colonnes du tableau en sortie). Parmi toutes ces variables, nous avons choisi ici de représenter height en fonction de weight, la hauteur en fonction de la masse des oursins. Jusqu’ici, nous avons spécifié ce que nous voulons représenter, mais pas encore comment (sous quelle apparence), nous voulons les matérialiser sur le graphique. Pour un nuage de points, nous voulons les représenter sous forme de … points ! Donc, nous devons ajouter la fonction geom_point() pour indiquer cela.

À vous de jouer !

Note : la vidéo ci-dessous vous expliquant la création du nuage de points dans R sur le jeu de données urchin est affublée du signe “H5P”, ce qui signifie qu’elle contient également des questions auxqeulles vous devez répondre dans le cadre de votre progression dans la matière.

h5p

Auto-évaluez maintenant vos acquis avec le tutoriel learnr suivant.

Effectuez maintenant les exercices du tutoriel A02Lc_nuage (Nuage de points).

BioDataScience1::run("A02Lc_nuage")

2.1.1 Echelles de graphiques

Vous devez être vigilant lors de la réalisation d’un nuage de point particulièrement sur l’étendue des valeurs présentées sur vos axes. Vous devez utilisez votre expertise de biologiste pour vous posez les deux questions suivantes :

  • Est ce que l’axe représente des valeurs plausibles de hauteurs et de masses de ces oursins appartenant à l’espèce Paracentrotus lividus ?

  • Quels est la précision des mesures effectuées ?

Dans certains cas, la forme du nuage de points peut être distendu par la présence de valeurs aberrantes. Ce n’est pas le cas ici, mais nous pouvons le simuler en distendant artificiellement soit l’axe X, soit l’axe Y, soit les deux :

Piège du nuage de points. A) graphique initial montrant la variation de la hauteur [mm] en fonction de la masse [g]. B) graphique A avec la modification de l'échelle de l'axe X. C) Graphique A avec une seconde modification de l'axe X. D) Graphique A avec modification simultanée des deux axes.

Figure 2.3: Piège du nuage de points. A) graphique initial montrant la variation de la hauteur [mm] en fonction de la masse [g]. B) graphique A avec la modification de l’échelle de l’axe X. C) Graphique A avec une seconde modification de l’axe X. D) Graphique A avec modification simultanée des deux axes.

À vous de jouer !

Note : l’exercice suivant est une application Shiny. Il s’agit d’un petit programme interactif écrit en R et qui vise à expérimenter librement avec un concept. Vous pouvez lancer cette exercice directement dans cette page ou l’exécuter dans RStudio à l’intérieur de votre machine virtuelle. Vérifiez d’être bien enregistré (message à l’ouverture de l’app) et n’oubliez pas de cliquer sur le bouton Submit pour tester votre choix, mais également sur le bouton Save & Quit pour valider définitivement votre réponse pour la prendre en compte dans votre rapport de progression.

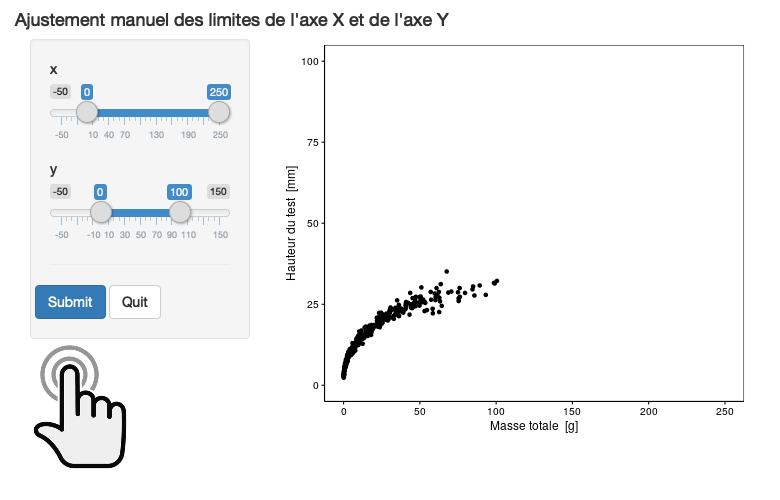Cliquez pour lancer ou exécutez dans RStudio BioDataScience1::run_app("A02Sa_limits").

2.1.2 Transformation des données

Vous avez la possibilité d’appliquer une transformation de vos données (il est même conseillé de le faire) afin qu’elles soient plus facilement analysables. Par exemple, il est possible d’utiliser des fonctions de puissance, racines, logarithmes, exponentielles4 pour modifier l’apparence du nuage de points dans le but de le rendre plus linéaire (car il est plus facile d’analyser statistiquement des données qui s’alignent le long d’une droite).

À vous de jouer !

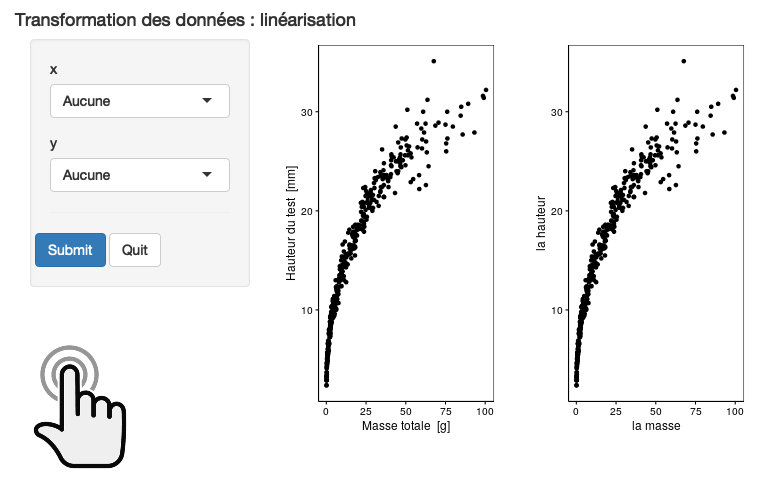Cliquez pour lancer ou exécutez dans RStudio BioDataScience1::run_app("A02Sa_transformation").

Pièges et astuces

RStudio permet de récupérer rapidement des instructions à partir d’une banque de solutions toutes prêtes. Cela s’appelle des snippets. Vous avez une série de snippets disponibles dans la SciViews Box. Celui qui vous permet de réaliser un graphique en nuage de points s’appelle .cbxy (pour chart -> bivariate -> xy-plot). Entrez ce code et appuyez ensuite sur la tabulation dans un script R, et vous verrez le code remplacé par ceci dans la fenêtre d’édition :

chart(data = DF, YNUM ~ XNUM) +
  geom_point()

Vous avez à votre disposition un ensemble de snippets que vous pouvez retrouver dans l’aide-mémoire consacré à SciViews. Vous avez également à votre disposition l’aide-mémoire sur la visualisation des données (Data Visualization Cheat Sheet) qui utilise la fonction ggplot() plutôt que chart() et une interface légèrement différente pour spécifier les variables à utiliser pour réaliser le graphique (aes(x = ..., y = ...)).

À vous de jouer !

Note : pour rappel, le travail ci-dessous est une assignation GitHub. Créez le dépôt GitHub relatif à cette assignation, ensuite clonez-le dans shared/projects dans votre machine virtuelle et vous aurez un nouveau projet RStudio B.1.1 dans lequel vous pourrez travailler.

Réalisez l’assignation A02Ga_nuagepoints, partie I.

Assignation GitHub Classroom pour les étudiants inscrits au cours de Science des Données Biologiques I à l’UMONS

Assignation GitHub Classroom pour les étudiants inscrits au cours de Bio-Informatique et Science des Données à Charleroi

Si vous êtes un utilisateur non enregistré ou que vous travaillez en dehors d’un cours, faites un “fork” de ce dépôt.

Voyez les explications dans le fichier README.md, partie I.

Inspirez-vous du script dans le dépôt sdd1_iris. Vous devez commencer par faire un “fork” du dépôt, puis un clone sur votre ordinateur en local pour pouvoir l’utiliser.

Prêtez une attention toute particulière à l’organisation d’un script R. En plus des instructions R, il contient aussi sous forme de commentaires, un titre , la date de la dernière mise à jour, le nom de l’auteur, et des sections qui organisent de façon claire le contenu du script. A ce sujet, vous trouverez des explications détaillées concernant l’utilisation des scripts R dans l’annexe B.1.2.

Pour en savoir plus

  1. Dans R, une formule permet de spécifier les variables avec lesquelles on souhaite travailler, et leur rôle. Par exemple ici, la variable x sur l’axe des abscisses et la variable y sur l’axe des ordonnées.↩︎

  2. Pour les proportions (prop) ou les pourcentages (perc) (valeurs bornées entre 0 et 1 ou 0 et 100%) la transformation arc-sinus est souvent utilisée : \(prop′ = \arcsin \sqrt{prop}\) ou \(perc′ = \arcsin \sqrt{perc / 100}\).↩︎