9.6 Représentation graphique
Il n’existe pas un graphique de référence afin de présenter un test t de Student ou un test de Wilcoxon. On retrouve malheureusement dans la littérature plusieurs graphiques qui coexistent. Afin de présenter 3 graphiques courants, nous utilisons le jeu de données crabs.
On retrouve généralement 2 graphiques montrant la moyenne et l’intervalle de confiance.
a <- chart(data = crabs, rear ~ sex) +
stat_summary(geom = "col", fun.y = "mean") +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_cl_normal", fun.args = list(conf.int = 0.95))# Warning: `fun.y` is deprecated. Use `fun` instead.b <- chart(data = crabs, rear ~ sex) +
geom_jitter(alpha = 0.3, width = 0.2) +
stat_summary(geom = "point", fun.y = "mean", size = 2) +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_cl_normal", fun.args = list(conf.int = 0.95), size = 1)# Warning: `fun.y` is deprecated. Use `fun` instead.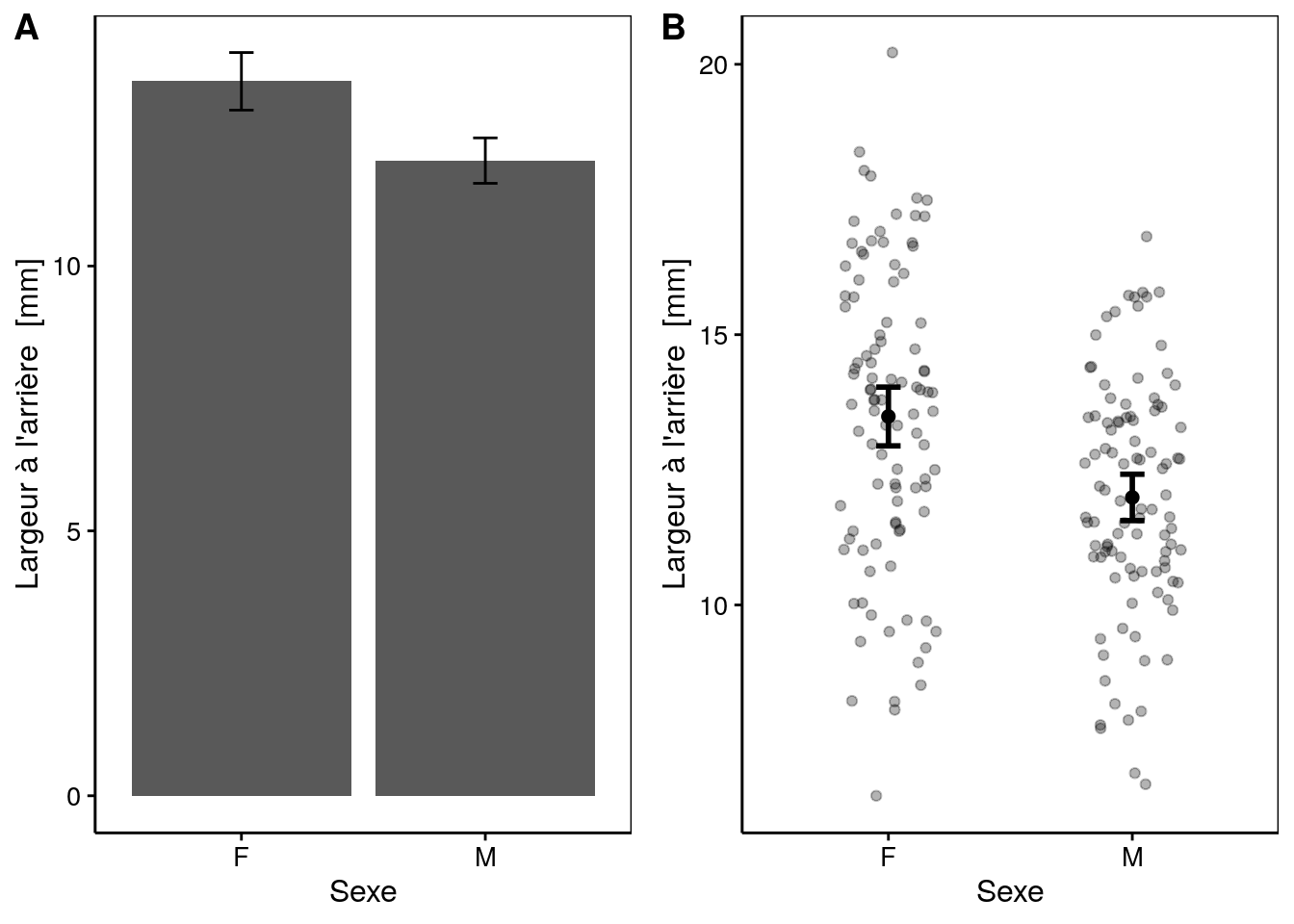
La graphique en barre et le nuage de point représentent identiquement la information. Ils représentent la moyenne avec des barres erreurs qui représentent l’intervalle de confiance à 0.95. Le graphe en dynamite avec des barres d’erreurs ne donne aucune information sur le nombre d’observation. Nous avons déja abordé rapidement cette problématique dans la section 4.1.3. Il n’est donc pas le graphique optimal pour présenter un test t de Student.
Malgré le fait que le test t de Student est un test paramétrique, on retrouve dans la littérature scientifique la boite de dispersion qui est pourtant un graphique associé à des valeurs non paramétriques. Pour le test de wilcoxon, la boite de dispersion est l’outil graphique recommandé.
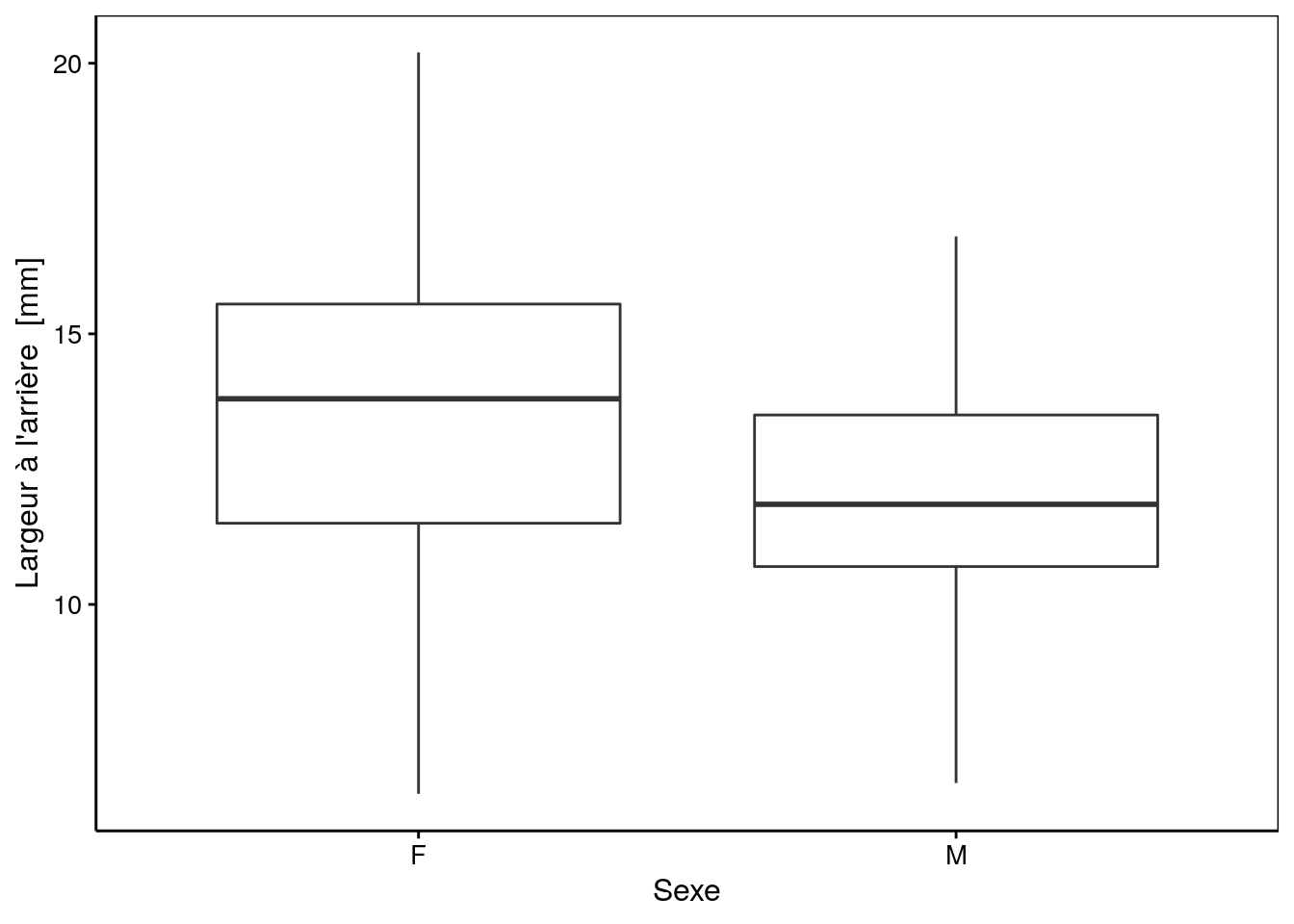
Parmi ces 3 choix, nous vous conseillons d’employer le nuage de point avec la valeur moyenne et l’intervalle de confiance.
chart(data = crabs, rear ~ sex) +
geom_jitter(alpha = 0.3, width = 0.2) +
stat_summary(geom = "point", fun.y = "mean") +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_cl_normal", fun.args = list(conf.int = 0.95))# Warning: `fun.y` is deprecated. Use `fun` instead.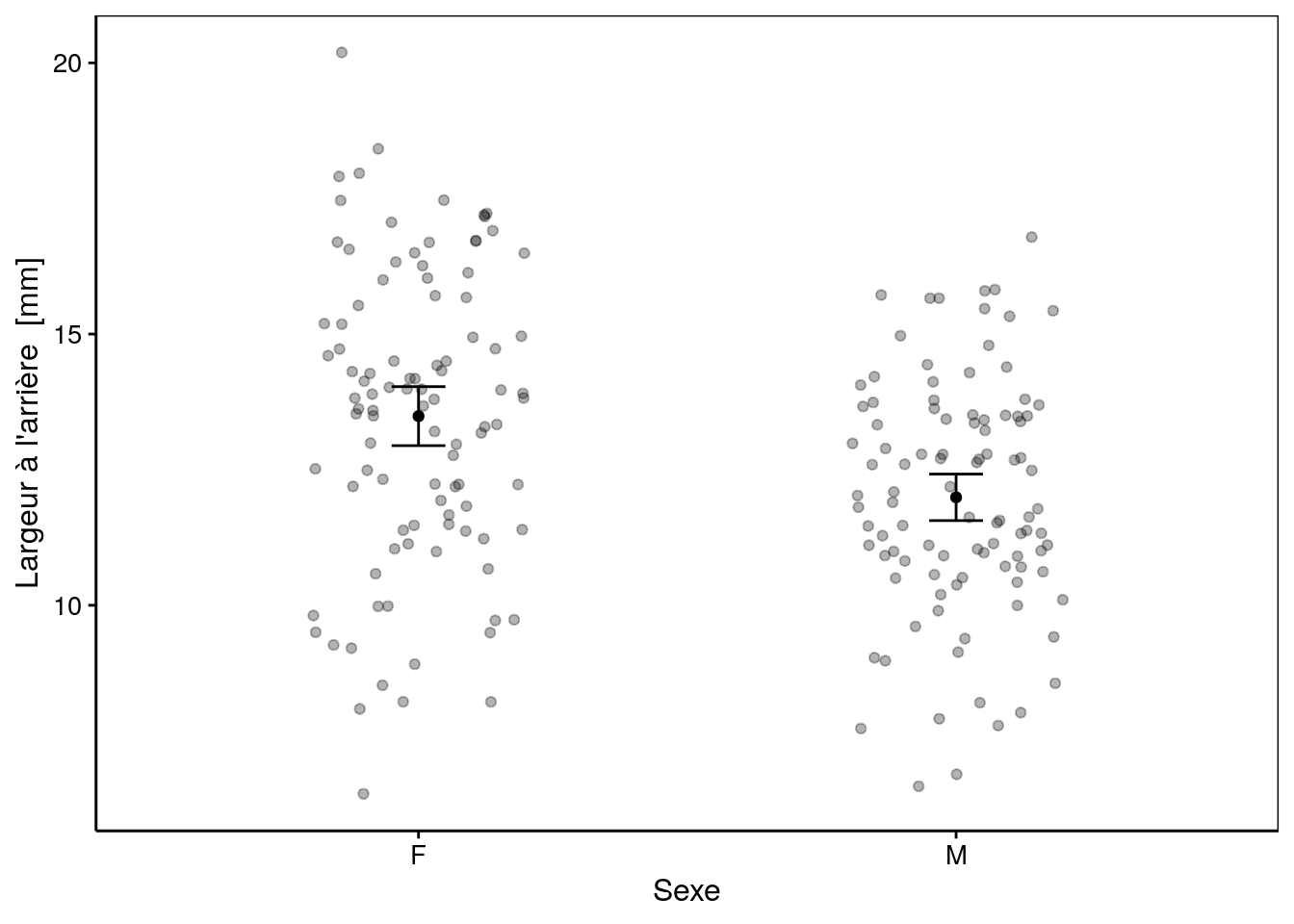
Pièges et astuces : barres d’erreurs
Que vous utilisiez le nuage de points ou le graphique en barres, vous devez être extrêmement vigilant aux barres d’erreurs. Vous devez toujours préciser et bien comprendre ce que les barres d’erreurs cachent. Voici 4 graphiques qui présentent différentes barres d’erreurs (la taille de l’axe y a volontairement été figée).
p <- chart(data = crabs, rear ~ sex) +
geom_jitter(alpha = 0.1, width = 0.2) +
stat_summary(geom = "point", fun.y = "mean") +
scale_y_continuous(limits = c(5,22))# Warning: `fun.y` is deprecated. Use `fun` instead.a <- p +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_cl_normal", fun.args = list(conf.int = 0.95))
b <- p +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_sdl", fun.args = list(mult = 1))
c <- p +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_sdl", fun.args = list(mult = 2))
d <- p +
stat_summary(geom = "errorbar", width = 0.1,
fun.data = "mean_se", fun.args = list(mult = 1))
combine_charts(list(a,b,c,d))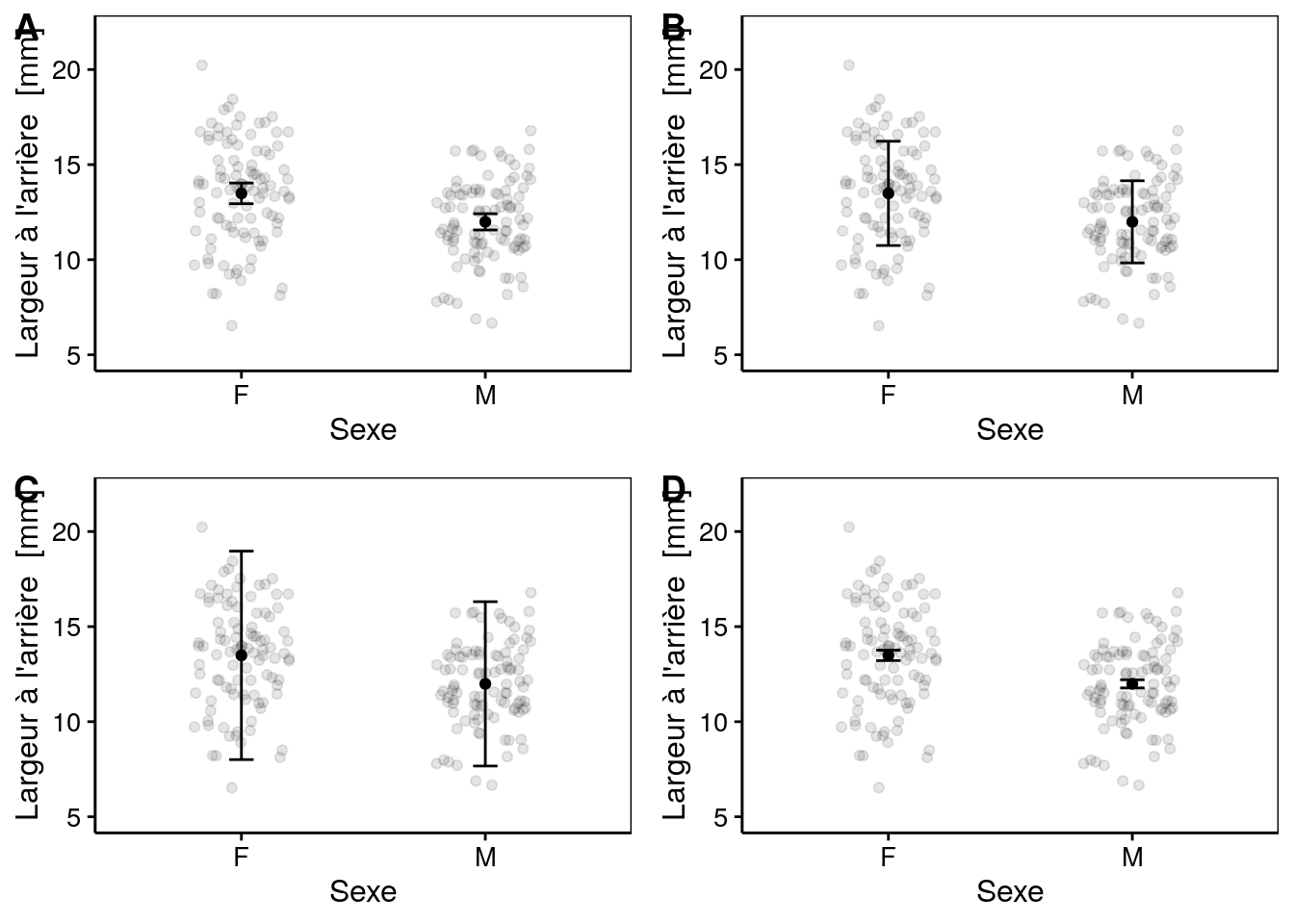
Figure 9.8: Nuage de points de la largeur de l’arrière de la carapace en focntion du sexe avec la moyenne et des barres d’erreurs. Graphe A : moyenne et intervalle de confiance 0.95. Graphe B : moyenne et écart-type. Graphe C : moyenne et 2*écart-type. Graphe D : moyenne et erreur standard
Les formules associées aux barres d’erreurs sont les suivantes de A à D:
- Graphe A : l’intervalle de confiance 0.95
\[\mathrm{IC}(1 - \alpha) \simeq \bar{x} \pm t_{\alpha/2}^{n-1} \cdot SE_x\]
# y ymin ymax
# 1 12.7385 12.37968 13.09732- Graphe B : l’écart-type
\[s_x = \sqrt{\sum_{i=1}^n{\frac{(x_i - \bar{x})^2}{n-1}}}\]
# y ymin ymax
# 1 12.7385 10.16516 15.31184- Graphe C : deux fois la valeur de l’écart-type
\[2 \times s_x\]
# y ymin ymax
# 1 12.7385 7.59182 17.88518- Graphe D : l’erreur standard
\[SE_x = \frac{s_x}{\sqrt{n}}\]
# y ymin ymax
# 1 12.7385 12.55654 12.92046Comme nous venons de le voir, les barres d’erreurs sont calculées à partir de différentes fonctions. Il est donc indispensable de préciser explicitement ce que les barres d’erreurs représentent.
Pour en savoir plus
Beware of dynamite. Démonstration de l’impact d’un graphe en barres pour représenter la moyenne (et l’écart type) = graphique en “dynamite”.
Dynamite plots : unmitigated evil? Une autre comparaison du graphe en dynamite avec des représentations alternatives qui montre que le premier peut avoir quand même quelques avantages dans des situations particulières.
Comparaison de moyennes : indiquez la significativité des différences sur le graph. Tutoriel sur la comparaison de moyennes avec
ggpubr
Pour terminer, bien que la moyenne soit un descripteur statistique très utile, il est parfois utilisé de manière abusive. Une distribution statistique ne se résume pas à un nombre, fût-ce la moyenne. De plus, si la distribution est asymétrique, la moyenne est un mauvais choix (préférer alors la médiane, ou transformer les données pour rendre la distribution plus symétrique). La vidéo suivante détaille le problème qui peut se produire :
À vous de jouer !
Appliquez vos nouvelles connaissances dans l’assignation de groupe que vous avez débutée lors du module précédent.
Réalisez en groupe l’assignation A08Ga_human_health, partie II.
Si vous êtes un utilisateur non enregistré ou que vous travaillez en dehors d’un cours, faites un “fork” de ce dépôt.
Voyez les explications dans le fichier README.md, partie II.
Note : Ce projet est la continuité d’un projet débuté lors que premier quadrimestre. l’assignation GitHub suivante est un exercice à réaliser en binôme. Ce projet est également transmodule, ce qui signifie que vous reviendrez dessus à plusieurs reprises au fur et à mesure de votre progression dans la matière afin de compléter votre analyse de ces données, toujours en binômes. Vous formez les binômes librement comme bon vous semble.
Réalisez en groupe l’assignation A03Ga_urchin, partie II.
Si vous êtes un utilisateur non enregistré ou que vous travaillez en dehors d’un cours, faites un “fork” de ce dépôt.
Voyez les explications dans le fichier README.md, partie II.