7.5 Distribution de poisson

Maintenant, nous pouvons poser la question autrement. Prenons un couple sain au hasard en Belgique, quelle est la probabilité que ce couple transmette la mucoviscidose à leur descendance ? Ne considérons pas ici les personnes elles-même atteintes de la maladie qui prendront certainement des précautions particulières. Sachant qu’une personne sur 20 est porteuse du gène défectueux (hétérozygote) dans la population saine belge, la probabilité de former un couple doublement hétérozygote qui pourrait transmettre la maladie est de34 :

1/20 * 1/20
# [1] 0.0025

… soit un couple sur 400. Donc, globalement, les probabilités d’avoir des enfants sains est beaucoup plus grande que 0.75 si nous incluons tous les couples belges de parents sains porteurs ou non. Cette probabilité est de35 :

(399 * 1 + 1 * 0.75) / 400
# [1] 0.999375

Pour un couple au hasard sans connaissance a priori du fait que les parents soient porteurs ou non, la probabilité d’avoir un enfant atteint de la mucoviscidose est heureusement très, très faible, mais non nulle (de l’ordre de 1/1600 = 0,000625 = 1 - 0.999375). Si nous considérons maintenant une population suffisamment grande pour pouvoir espérer y trouver “statistiquement” une personne atteinte de mucoviscidose, nous pourrions décider d’étudier un échantillon aléatoire de 1600 enfants belges. La distribution binomiale requiert alors le calcul de \(C^j_n\) sur base de \(n = 1600\), ce qui revient à devoir calculer le factoriel de 1600 :

factorial(1)
# [1] 1
factorial(10)
# [1] 3628800
factorial(100)
# [1] 9.332622e+157
factorial(1600)
# [1] Inf

Or, le factoriel est un nombre qui grandit très, très vite. Déjà le factoriel de 100 est un nombre à 157 chiffres. Nous voyons que R est incapable de calculer précisément le factoriel de 1000. Ce nombre est supérieur au plus grand nombre que l’ordinateur peut représenter pour un double en R (1.797693110^{308}). Donc, nous sommes incapables de répondre à la question à l’aide de la loi binomiale à cause du passage nécessaire par un calcul du factoriel de très grands nombres.

7.5.1 Évènements rares

La distribution de Poisson permet d’obtenir la réponse à la question posée parce qu’elle effectue le calcul différemment. Cette distribution discrète a un seul paramètre \(\lambda\) qui représente le nombre moyen de cas rares que l’on observe dans un échantillon donné, ou sur un laps de temps fixé à l’avance. Cette distribution est asymétrique pour de faible \(\lambda\). Les conditions d’application sont :

  • résultat binaire,
  • essais indépendants (les probabilités ne changement pas d’un essai à l’autre),
  • taille d’échantillon ou laps de temps que le phénomène est observé fixe,
  • probabilité d’observation de l’évènement \(\lambda\) faible.

Pour une variable \(Y \sim P(\lambda)\), nous pouvons calculer la probabilité que \(Y = 0\), \(Y = 1\), … de la façon suivante :

\[P(Y=0) = e^{-\lambda}\]

et

\[P(Y=k) = P(Y=k-1) \times \frac{\lambda}{k}\]

Le calcul se réalise de proche en proche en partant de la probabilité de ne jamais observer l’évènement. Comme l’évènement est rare, la probabilité tend très rapidement vers une valeur extrêmement faible. Seul le calcul des quelques premiers termes est donc nécessaire. A titre d’exercice, faites le calcul pour notre exemple d’un échantillon de la population belge, avec \(\lambda = 1\) comme paramètre. La densité de probabilité pour cette distribution est représentée à la Fig. 7.8.

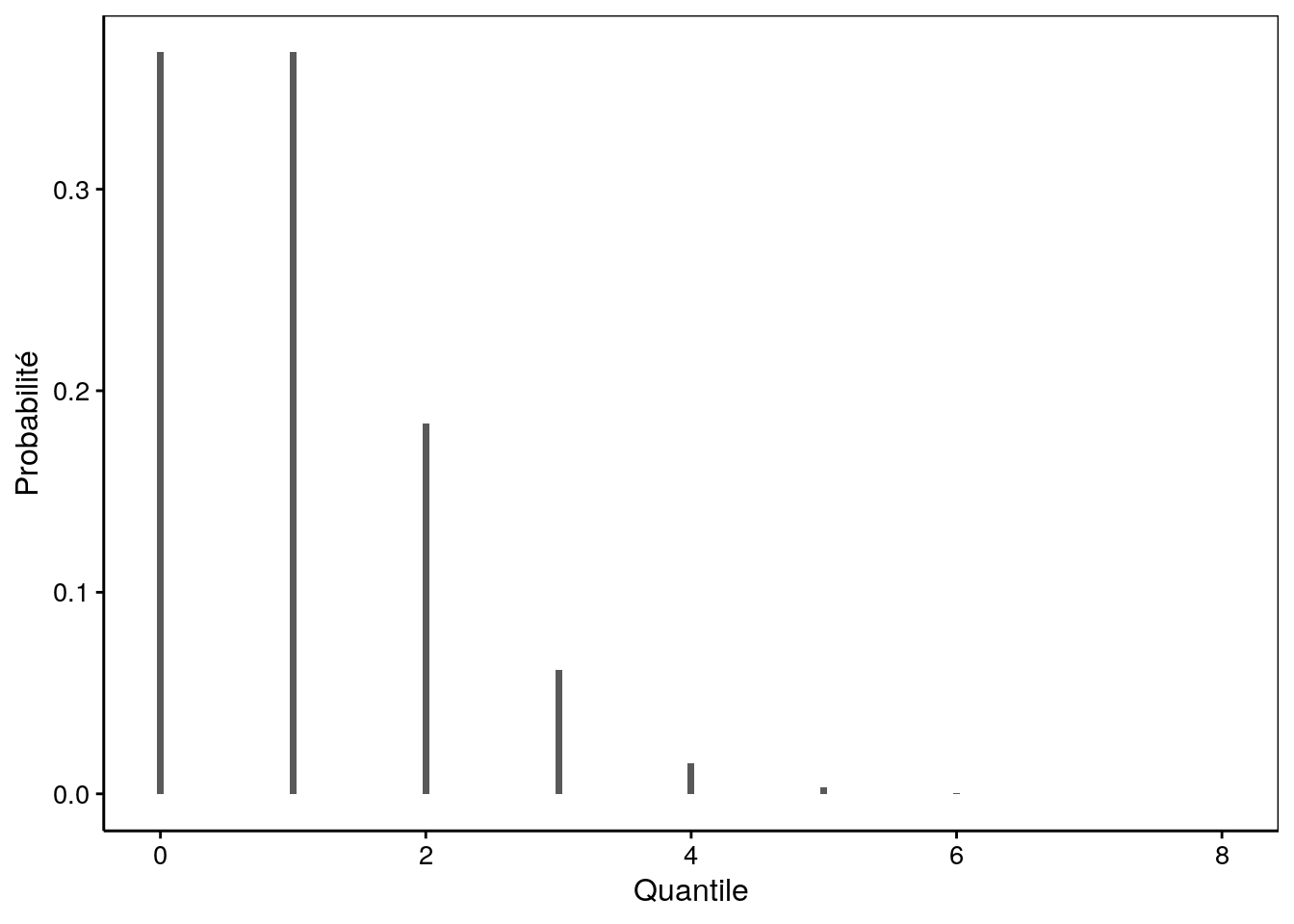
Probabilité d'occurence de mucoviscidose dans un échantillon aléatoire de 1600 belges.

Figure 7.8: Probabilité d’occurence de mucoviscidose dans un échantillon aléatoire de 1600 belges.

7.5.2 Loi de Poisson dans R

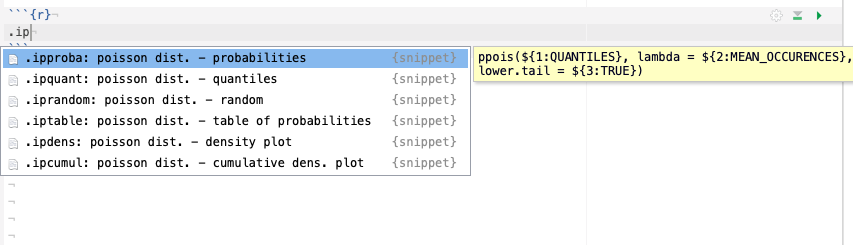
Les fonctions dans R relatives à la distribution de Poisson portent des noms <x>pois(), tel que ppois() pour calculer des probabilités, qpois() pour calculer des quantiles ou rpois() pour générer des nombres pseudo-aléatoires selon cette distribution. Voici la liste des snippets à votre disposition dans la SciViews Box pour vous aider (menu (d)istributions: poisson à partir de .ip) :

À vous de jouer !

Effectuez maintenant les exercices du tutoriel A07Lb_distri (Lois de distributions).

BioDataScience1::run("A07Lb_distri")

  1. Comme il y a la même proportion d’hommes et de femmes porteurs, nous avons 1/20 des hommes et 1/20 des femmes qui sont porteurs. Nous formons des couples au hasard en piochant un homme dans la population masculine et une femme dans la population féminine de manière indépendante. Dans ce cas, nous obtenons un couple double porteur à une fréquence de 1/20 * 1/20 = 1/400.↩︎

  2. Sur 400 couples, 399 ont une probabilité d’engendrer des enfants sains (porteurs hétérozygotes ou non porteurs confondus) de 100%. A cela il faut ajouter un couple sur 400 qui aura une probabilité de 75% de faire des enfants non atteints car non homozygotes.↩︎