4.2 Qu’est-ce qu’une série chronologique ?

Lorsque nous mesurons de manière répétée le même individu à des moments différents, nous parlons de série chronologique, de séries temporelles, ou de série spatio-temporelle (space-time series en anglais). Ce dernier terme “spatio-temporel” se réfère, en réalité, à un axe unidimensionnel que nous représentons toujours par convention sur l’axe des abscisses sur un graphique et le long duquel nos observations varient. Il peut s’agir du temps, ou d’une dimension spatiale linéaire (mesures le long d’un transect, comme nous l’avons vu pour le plancton méditerranéen), ou d’un mélange des deux c’est-à-dire que le temps se déroule alors que nous progressons dans nos mesures le long du transect. Quoi qu’il en soit, le fait de mesurer toujours le même individu ou la même entité mène à une interdépendances des observations les unes par rapport aux autres.

Cette propriété de corrélation au sein de la série entre les observations est dite autocorrélation. C’est la caractéristique principale d’une série temporelle que de contenir une autocorrélation non nulle (dans le cas contraire, on parle de bruit blanc, white noise en anglais). C’est cette autocorrélation qui fait que l’hypothèse d’indépendance des observations entre elles n’est pas respectée, et comme corollaire, que nous ne pouvons pas utiliser les outils de statistique classique lorsque nous avons affaire à des séries temporelles.

Donc, nous devons utiliser des outils statistiques spécialisés qui tiennent compte de l’autocorrélation. Il faut aussi noter que cette autocorrélation, si elle est très forte, peut être utilisée à notre avantage. En effet, nous pouvons imaginer prédire la valeur que prendra la variable mesurée dans la série au temps \(t + \Delta t\), connaissant uniquement la valeur qu’elle prend au temps \(t\) (et peut-être aussi, au temps \(t - \Delta t\), \(t - 2 \Delta t\), \(t - 3 \Delta t\), …). Nous appellerons \(\Delta t\), l’intervalle temporel entre deux mesures successives, le pas de temps de notre série.

Une autre caractéristique importante des séries temporelles est l’existence de cycles. En effet, de nombreux phénomènes sont périodiques dans le temps (cycles circadiens, lunaires, annuels, etc.) et ils influent sur les biologie et l’écologie des êtres vivants. Il n’est donc pas étonnant de retrouver des cycles similaires dans les séries temporelles en biologie. Plusieurs méthodes existent également pour étudier et/ou extraire des cycles ou des tendances à plus long terme du bruit de fond contenu dans les séries temporelles. Nous verrons ici quelques uns de ces outils.

Au cours de notre exploration des séries temporelles, nous aborderons les fonctions standard de R pour la manipulation et l’analyse des séries temporelles. Nous aborderons aussi des outils plus spécialisés contenus dans les packages {pastecs} (“Package for the Analysis of Space-Time Ecological Series”) et {xts} (“eXtensible Time Series”). Nous allons successivement étudier comment créer et manipuler des séries temporelles dans R et comment les décrire. Dans le module suivant, nous poursuivrons en apprenant à les décomposer, et enfin, nous verrons comment régulariser des séries irrégulières.

4.2.1 Séries régulières

Une série régulière est un ensemble de données mesurées sur la même entité (même individu, même unité statistique) avec un espacement constant dans le temps (ou le long d’un transect). La série n’a pas de valeurs manquantes. Ce type de série a des avantages énormes car nous pouvons décaler la série d’un ou plusieurs pas de temps, et les observations après décalage correspondent aux mêmes dates que les observations originales, à part aux extrémités, bien entendu.

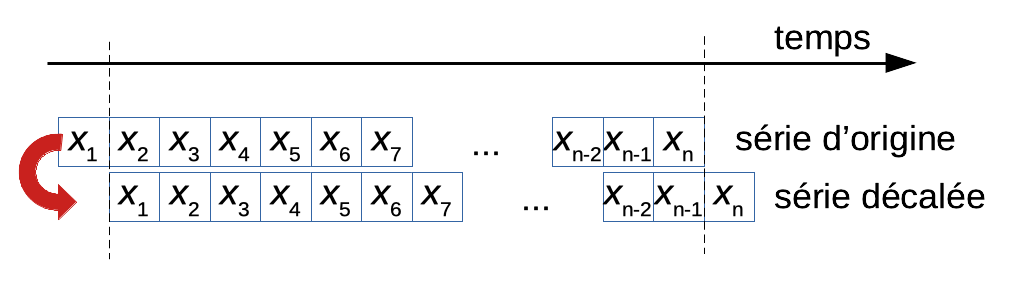
Le décalage d’une série régulière d’un pas de temps résulte en des observations aux mêmes dates, mais décalées d’une unité : x1 est maintenant à la même date que x2 avant le décalage, x2 à la même date que x3 avant, et ainsi de suite…
Le décalage d’une série régulière d’un pas de temps résulte en des observations aux mêmes dates, mais décalées d’une unité : x1 est maintenant à la même date que x2 avant le décalage, x2 à la même date que x3 avant, et ainsi de suite…

Après avoir effectué un décalage (lag en anglais) de un pas de temps, et moyennant l’élimination de la première observation x1 de la série d’origine et la dernière observation xn de la série décalée, nous obtenons un tableau de 2 lignes et n - 1 colonnes. Nous noterons l’opérateur de décalage ou opérateur retard L, un opérateur qui effectue exactement ce traitement, c’est-à-dire qu’il associe à tout élément de la série régulière, l’observation précédente.

\[L X_t = X_{t-1}\]

Nous pouvons calculer la corrélation \(r\), par exemple à l’aide du coefficient de corrélation de Pearson (ou de Spearman) entre les deux lignes du tableau obtenu en accolant la série de départ \(X_t\) et la même série décalée \(LX_t\), amputées des extrémités ne comportant pas de paires d’observations (la version de Spearman se calculera sur les rangs des observations, voir module 12 du cous SDD I) :

\[r_{X_t,LX_t} = \frac{cov_{X_t,LX_t}}{\sqrt{S^2_{X_t} + S^2_{LX_t}}}\]

Avec \(cov\) la covariance et \(S^2\) la variance. Cette corrélation étant calculée entre la série et elle-même, elle est appelée autocorrélation. Par simplicité, nous pouvons aussi noter le décalage choisi “tau” (\(\tau\)), et nous aurons alors l’autocorrélation correspondante à ce décalage qui sera notée \(r(\tau)\) avec \(\tau = 1\). Naturellement, nous pouvons décaler de plus de un pas de temps. Par exemple, si nous décalons de deux pas de temps, l’opérateur correspondant s’appelle alors L2 :

\[L^2 X_t = X_{t-2}\]

Ce calcul correspond au schéma suivant :

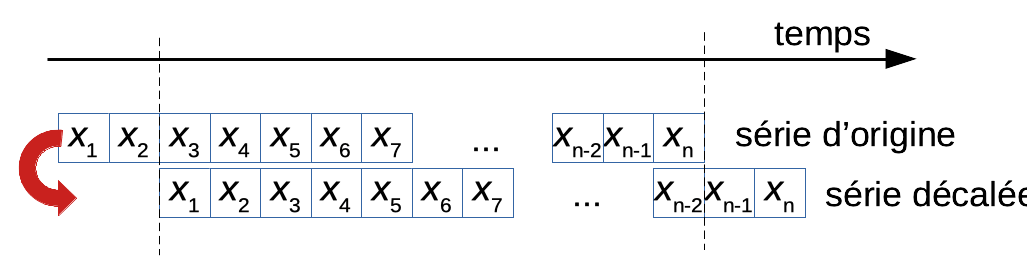
Décalage de deux pas de temps (L2) : x1 est maintenant à la même date que x3 avant le décalage, x2 à la même date que x4, etc.
Décalage de deux pas de temps (L2) : x1 est maintenant à la même date que x3 avant le décalage, x2 à la même date que x4, etc.

Si nous voulons rassembler la série de départ X et la série décalée L2 X, nous sommes maintenant obligés de laisser tomber les deux premières observations de X et les deux dernières de L2 X. Nous pouvons naturellement aussi calculer l’autocorrélation \(r_{X_t,L^2X_t}\), ou encore, \(r(\tau)\) pour \(\tau = 2\).

De manière générale, nous définissons Lk, avec k pouvant prendre des valeurs entières positives ou négatives (la série est décalée dans l’autre sens).

\[L^k X_t = X_{t-k}\]

L0 est un cas particulier où la série est simplement recopiée aux mêmes dates. Comme la corrélation entre une série et elle-même est toujours parfaite, \(r(\tau) = 1\) toujours pour \(\tau = 0\). L’autocorrélation pour un décalage nul vaut toujours un. Notez que \(r(\tau)\) est en fait une fonction dépendant de variations discrètes de \(\tau\). On l’appelle donc la fonction d’autocorrelation (autocorrelation fonction en anglais). Cette fonction d’autocorrélation est un merveilleux outil pour analyser les caractéristiques de notre série… nous y reviendrons donc dans la partie analyse plus loin.

R propose un type d’objet particulier pour représenter des séries régulières univariées (une seule variable mesurée à chaque fois) : les objets ts. Nos trois séries d’exemples de la section précédent sont des objets de ce type. Prenons lynx et examinons comment cet objet est représenté.

data("lynx", package = "datasets")
lynx
# Time Series:
# Start = 1821 
# End = 1934 
# Frequency = 1 
#   [1]  269  321  585  871 1475 2821 3928 5943 4950 2577  523   98  184  279  409
#  [16] 2285 2685 3409 1824  409  151   45   68  213  546 1033 2129 2536  957  361
#  [31]  377  225  360  731 1638 2725 2871 2119  684  299  236  245  552 1623 3311
#  [46] 6721 4254  687  255  473  358  784 1594 1676 2251 1426  756  299  201  229
#  [61]  469  736 2042 2811 4431 2511  389   73   39   49   59  188  377 1292 4031
#  [76] 3495  587  105  153  387  758 1307 3465 6991 6313 3794 1836  345  382  808
#  [91] 1388 2713 3800 3091 2985 3790  674   81   80  108  229  399 1132 2432 3574
# [106] 2935 1537  529  485  662 1000 1590 2657 3396

Visiblement, à l’impression de lynx, on voit que c’est un objet particulier “Time Series”.

class(lynx) # Objet ts
# [1] "ts"

De même, la fonction de {pastecs} is.tseries() renvoie TRUE si l’objet est une des formes de séries temporelles de R :

library(pastecs)
# 
# Attachement du package : 'pastecs'
# The following objects are masked _by_ '.GlobalEnv':
# 
#     marbio, marphy
# The following objects are masked from 'package:dplyr':
# 
#     first, last
# The following object is masked from 'package:tidyr':
# 
#     extract
is.tseries(lynx)
# [1] TRUE

Pour inspecter (aux rayons X) un objet dans R, on peu le “déclasser” avec unclass(), ce qui a pour effet d’imprimer son contenu.

unclass(lynx)
#   [1]  269  321  585  871 1475 2821 3928 5943 4950 2577  523   98  184  279  409
#  [16] 2285 2685 3409 1824  409  151   45   68  213  546 1033 2129 2536  957  361
#  [31]  377  225  360  731 1638 2725 2871 2119  684  299  236  245  552 1623 3311
#  [46] 6721 4254  687  255  473  358  784 1594 1676 2251 1426  756  299  201  229
#  [61]  469  736 2042 2811 4431 2511  389   73   39   49   59  188  377 1292 4031
#  [76] 3495  587  105  153  387  758 1307 3465 6991 6313 3794 1836  345  382  808
#  [91] 1388 2713 3800 3091 2985 3790  674   81   80  108  229  399 1132 2432 3574
# [106] 2935 1537  529  485  662 1000 1590 2657 3396
# attr(,"tsp")
# [1] 1821 1934    1

Ici, nous voyons qu’il s’agit d’un vecteur de données numériques auquel est ajouté un attribut (attr) nommé tsp pour time series parameters et qui contient trois valeurs : 1821, 1934 et 1. Où sont les données de temps ? Et que veulent dire ces valeurs de tsp ? En fait, pour économiser de la place en mémoire, R n’enregistre pas toutes les dates, mais seulement la première, la dernière et le pas de temps de la série dans tsp. a l’aide de ces trois valeurs il est en fait possible de reconstituer toutes les dates. La fonction time() s’en charge :

time(lynx)
# Time Series:
# Start = 1821 
# End = 1934 
# Frequency = 1 
#   [1] 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835
#  [16] 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850
#  [31] 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865
#  [46] 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 1879 1880
#  [61] 1881 1882 1883 1884 1885 1886 1887 1888 1889 1890 1891 1892 1893 1894 1895
#  [76] 1896 1897 1898 1899 1900 1901 1902 1903 1904 1905 1906 1907 1908 1909 1910
#  [91] 1911 1912 1913 1914 1915 1916 1917 1918 1919 1920 1921 1922 1923 1924 1925
# [106] 1926 1927 1928 1929 1930 1931 1932 1933 1934

Nous obtenons un autre objet ts qui contient cette fois-ci les dates de chaque observation. Le troisième nombre de tsp est la fréquence des observations (ici, 1) par rapport à l’unité de temps choisie (ici l’année). A partir de ces trois nombres, nous pouvons donc reconstituer la séquence des années depuis 1821 jusqu’à 1934 auxquelles les observations ont été réalisées.

Comment connaître l’unité de temps utilisée dans la série ? En fait, cette unité n’est pas stockée dans l’objet ts. Vous la choisissez librement, vous définissez la date de départ, la date de fin exprimés dans cette unité choisie, ainsi que la fréquence des observations, et votre attribut tsp est complètement défini. La fonction ts() permet de générer une série temporelle, ou de transformer un vecteur d’observations en une série temporelle. Par exemple, si nous générons des données artificielles à partir d’une distribution Normale avec rnorm(), et que nous considérons ces données comme une série chronologique mesurée mensuellement entre janvier 2010 et décembre 2014, nous ferions ceci :

fake_ser <- ts(rnorm(5 * 12), start = 2010, frequency = 12)
fake_ser
#              Jan         Feb         Mar         Apr         May         Jun
# 2010  0.33276411  0.66480010  0.78081969 -0.80558932  1.27484733 -1.07926363
# 2011  2.54164018 -0.60340160  1.45171120 -2.28800156 -1.53784331 -1.61409886
# 2012 -0.36334814 -0.56905164 -0.08793338  0.22007130  0.08072106 -0.03184569
# 2013 -0.81389959  0.93752651  2.65404877  0.15000252  0.66844304 -0.82838731
# 2014  0.86920348  0.90742916 -0.55337746  0.60886286 -0.23233407  0.21748908
#              Jul         Aug         Sep         Oct         Nov         Dec
# 2010  0.82425467 -1.09953578 -1.62153527 -1.51898774 -0.95785049 -1.35779032
# 2011  1.28867327 -0.11939720 -0.37034715 -0.45481942  0.93236964  0.93389445
# 2012  0.69479980 -0.49097350  0.55629556 -1.07023525  1.39517849 -1.12115037
# 2013 -1.83571289  2.39463318 -0.59442328  1.61860177 -0.52639859 -0.45531895
# 2014  0.01651689  0.86433498  1.20429809 -0.04913012 -1.69600516  1.13857560

Notez comme R formate notre sortie (il assume qu’une série à fréquence de 12 correspond à des données mensuelles). Nous ne devons indiquer que deux des trois paramètres de tsp, car le nombre d’observations dans le vecteur fournit l’information manquante à ts(). Quelles sont les dates de ces observations ?

time(fake_ser)
#           Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
# 2010 2010.000 2010.083 2010.167 2010.250 2010.333 2010.417 2010.500 2010.583
# 2011 2011.000 2011.083 2011.167 2011.250 2011.333 2011.417 2011.500 2011.583
# 2012 2012.000 2012.083 2012.167 2012.250 2012.333 2012.417 2012.500 2012.583
# 2013 2013.000 2013.083 2013.167 2013.250 2013.333 2013.417 2013.500 2013.583
# 2014 2014.000 2014.083 2014.167 2014.250 2014.333 2014.417 2014.500 2014.583
#           Sep      Oct      Nov      Dec
# 2010 2010.667 2010.750 2010.833 2010.917
# 2011 2011.667 2011.750 2011.833 2011.917
# 2012 2012.667 2012.750 2012.833 2012.917
# 2013 2013.667 2013.750 2013.833 2013.917
# 2014 2014.667 2014.750 2014.833 2014.917

R mesure ici le temps sous forme décimale. C’est pratique, mais nous n’y sommes pas habitués. Ainsi, il divise l’année en 12 douzièmes, peu importe que certains mois contiennent 31, 30 ou même 28/29 jours. Ainsi, le 1er janvier 2010 est 2010.000. Le 1er février 2010 est 2010 + 1/12 = 2010.083. Et le 1er décembre 2014 est 2014 + 11/12 = 2014.917. La petite erreur de décalage du début de chaque mois est minime et sans impacts pratiques pour nos séries chronologiques biologiques car le vivant se soucie peu de notre calendrier grégorien. Par contre, pour des données comme le cours de la bourse, par exemple, ce genre d’approximation n’est pas utilisable et il faut alors employer des objets qui manipulent les dates de manière plus précise (mais aussi plus fastidieuse), que ceux du package {xts} (voir plus loin, les séries irrégulières).

Dans notre série fake_ser de fréquence 12, le pas de temps est donc de un mois, soit 1/12 d’année. Notez que le pas de temps est en fait l’inverse de la fréquence des observations. Si vous êtes plus à l’aise avec ce pas de temps, vous pouvez le substituer à la fréquence dans la fonction ts()via l’argument deltat=. Ainsi, indiquer ts(...., frequency = 12) ou ts(...., deltat = 1/12) est strictement équivalent.

Nous rencontrons également des objets mts pour multivariate time series. Ces objets contiennent plusieurs variables mesurées sur la même entité au cours du temps. Le vecteur est alors remplacé par une matrice à n lignes (le nombre d’observations dans le temps) et m colonnes (le nombre de variables mesurées à chaque fois). L’attribut tsp est le même que pour ts. La sélection des séries au sein de la matrice se fait à l’aide de l’opérateur “crochet” [,] où la ou les séries d’intérêt sont reprises en second argument après la virgule soit sous forme d’un vecteur d’entiers qui représentent les positions des colonnes à conserver, soit sous forme d’un vecteur de chaînes de caractères qui reprennent les noms des séries à conserver. Les séries multivariées marbio et marphy en sont des bons exemples. Les objets mts sont également des objets ts et des objets matrix (on dit qu’elles héritent de ces classes2) :

class(marphy)
# [1] "mts"    "ts"     "matrix"

Comme la température et la densité sont les première et quatrième colonnes de marphy, nous pouvons les extraire par position (et colnames() est utilisé pour renvoyer les noms des colonnes dans une matrice et donc par héritage, dans un objet mts) :

# Nom de toutes les séries dans marphy
colnames(marphy)
# [1] "Temperature"  "Salinity"     "Fluorescence" "Density"
# Nom après sélection de deux séries
colnames(marphy[, c(1, 4)])
# [1] "Temperature" "Density"

La sélection à l’aide des identifiants est souvent préférable, car plus explicite. Le même résultat est obtenu avec :

colnames(marphy[, c("Temperature", "Density")])
# [1] "Temperature" "Density"
N’essayez pas d’utiliser la sélection à l’aide de [,] sur un objet ts contenant une série univariée. Vous génèreriez une erreur car cet objet contient un vecteur et non pas une matrice. De plus, cela n’a aucun sens de faire une sélection parmi… une seule série dans cet objet !
À vous de jouer !
h5p

4.2.2 Séries à trous

Une série à trous est une série régulière, mais avec des valeurs manquantes. Comme R représente des valeurs manquantes dans un vecteur par NA, il est possible de créer et manipuler des séries à trous à l’aide des objets ts et mts. Par contre, certaines méthodes statistiques ne gérerons pas ces valeurs manquantes et refuseront de renvoyer un résultat.

En profitant des propriétés d’autocorrélation de la série, il est possible d’estimer des valeurs raisonnables pour remplacer les données manquantes si elles sont peu nombreuses. Par exemple, il est possible de faire une interpolation linéaire entre les deux observations qui encadrent la valeur manquante. Cette technique, et d’autres, seront abordées dans le module suivant dans la section relative à la régularisation. Retenez juste, à ce stade, que notre objectif sera de régulariser autant que possible une série à trous avant de l’analyser.

4.2.3 Séries irrégulières

Dès que le pas de temps entre les observations n’est pas constant, nous parlons de série irrégulière. Les séries irrégulières ne peuvent pas être représentées par des objets ts ou mts de R qui imposent un pas de temps régulier. Par contre, les packages {zoo} et {xts} permettent de manipuler ce genre de données.

TODO: introduction rapide à {xts} et conversion entre objets.

De manière générale, nous avons toujours intérêt à réaliser une séries régulière, ou la plus régulière possible. Ensuite, il faut penser aux techniques de régularisation si c’est faisable pour obtenir une série régulière qui approxime suffisamment bien les données de départ. En effet, la plupart des techniques d’analyse des séries temporelles se basent sur des séries régulières, et en tous cas celles du package {pastecs}.

À vous de jouer !
h5p
À retenir

  • Nous devons nous arranger pour obtenir autant que possible des séries régulières. Sinon, les séries à trous, voire légèrement irrégulières, pourront être régularisées avant analyses (voir module suivant).

  • R représente des séries régulières à l’aides d’objets ts (univariées) ou mts (multivariées).

  • Dans ces objets, le temps est encodé grâce à l’attribut tsp qui contient trois valeurs : la date de départ, celle de fin et la fréquence des observations.

  • L’unité de temps n’est pas définie par R : vous la choisissez librement. Si la fréquence est 12, R considérera toutefois à l’impression du contenu de l’objet que c’est des mesures mensuelles et que l’unité est l’année. De même si la fréquence est de 4, il considérera des mesures trimestrielles sur une année. Sinon, le temps est manipulé et imprimé par R de manière décimale.

  • Nous pouvons créer un objet ts ou mts à l’aide de la fonction ts(). Nous devons donner le vecteur ou la matrice des observations, ainsi que deux des trois paramètres de tsp. Nous pouvons substituer le pas de temps à la fréquence des observations via l’argument deltat=. En fait, deltat == 1/frequence, le pas de temps est l’inverse de la fréquence.

  • Les séries irrégulières doivent être représentées par des objets xts et le package {xts} propose une large palette de fonction pour manipuler de tels objets.

Pour en savoir plus