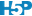2.6 Forêt alétoire
La forêt aléatoire, ou random forest en anglais (RF) est un algorithme introduit par Breiman (2001) qui créé un ensemble d’arbres décisionnels individuels, dont la variable discriminante à chaque nœud est choisie parmi un sous-ensemble aléatoire de toutes les p variables utilisées (afin d’introduire une variation aléatoire dans chaque arbre de partitionnement qui sont donc tous différents). Lorsque l’ensemble des arbres est créé, un vote à la majorité est appliqué en utilisant la réponse donnée par chaque arbre pour déterminer à quelle classe appartient l’individu étudié. C’est actuellement un des algorithmes les plus performants de classification supervisée. Par contre, étant donné qu’il faut créer plusieurs centaines d’arbres, le temps de calcul est généralement plus élevé qu’avec des méthodes simples comme ADL, k plus proches voisins, ou l’utilisation d’un arbre unique.
La combinaison de plusieurs classifieurs donne quasi-systématiquement des meilleurs résultats qu’un classifieur seul. On parle alors d’ensemble de classifieurs. La forêt aléatoire en est un excellent exemple. Plusieurs autres techniques existent pour combiner des classifieurs et améliorer les résultats, mais leur développement sort du cadre de ce cours :
stacking : Les résultats d’un ou plusieurs classifieurs sont utilisés comme variables d’entrée pour un autre classifieur. En d’autre terme, les classifieurs sont reliés en série les uns derrière les autres.
bagging : pour bootstrap aggregating améliore la stabilité et la précision de la classification. Quelques méthodes sont implémentées notamment dans le package R {ipred}. Le principe consiste à générer plusieurs sets d’apprentissage artificiellement par échantillonnage avec remplacement (technique de bootstrap), à entraîner des classifieurs sur chaque set, et à ensuite résumer les résultat via un vote à la majorité.
boosting : entraîne successivement des classifieurs en se focalisant sur les erreurs du précédent. L’un des algorithmes les plus performants actuellement, XGBoost fait partie de cette catégorie (voir le package {xgboost} dans R).
Les paramètres à définir sont le nombre d’arbres et le nombre de p attributs à choisir aléatoirement parmi tous les attributs à chaque nœud pour établir la règle de décision. C’est par cette présélection aléatoire de candidats de départ pour les règles que la variation est créée d’un arbre à l’autre. Cette présélection aléatoire est réitérée, naturellement, à chaque nœeud de chaque arbre. Les paramètres choisis ici sont de 500 arbres et de 2p/3 attributs conservés aléatoirement à chaque nœud. Ces valeurs se sont montrées efficaces dans des études antérieures, et l’algorithme est, par ailleurs, relativement robuste face aux variations de ces paramètres autour des valeurs par défaut.
2.6.1 Pima avec forêt aléatoire
La méthode de forêt aléatoire est disponible dans {mlearning}. Son utilisation est similaire aux autres fonctions du package, avec ici les arguments ntree = pour le nombre d’arbres, et mtry = pour le nombre de variables à sélectionne au hasard à chaque nœud. Par défaut, 500 arbres sont construits et les 2/3 des variables sont utilisées. Voyons ce que cela donne avec ces valeurs par défaut :
library(mlearning)
pima1_rf <- mlRforest(data = pima1, diabetes ~ .)
set.seed(74356)
pima1_rf_conf <- confusion(cvpredict(pima1_rf, cv.k = 10), pima1$diabetes)
plot(pima1_rf_conf)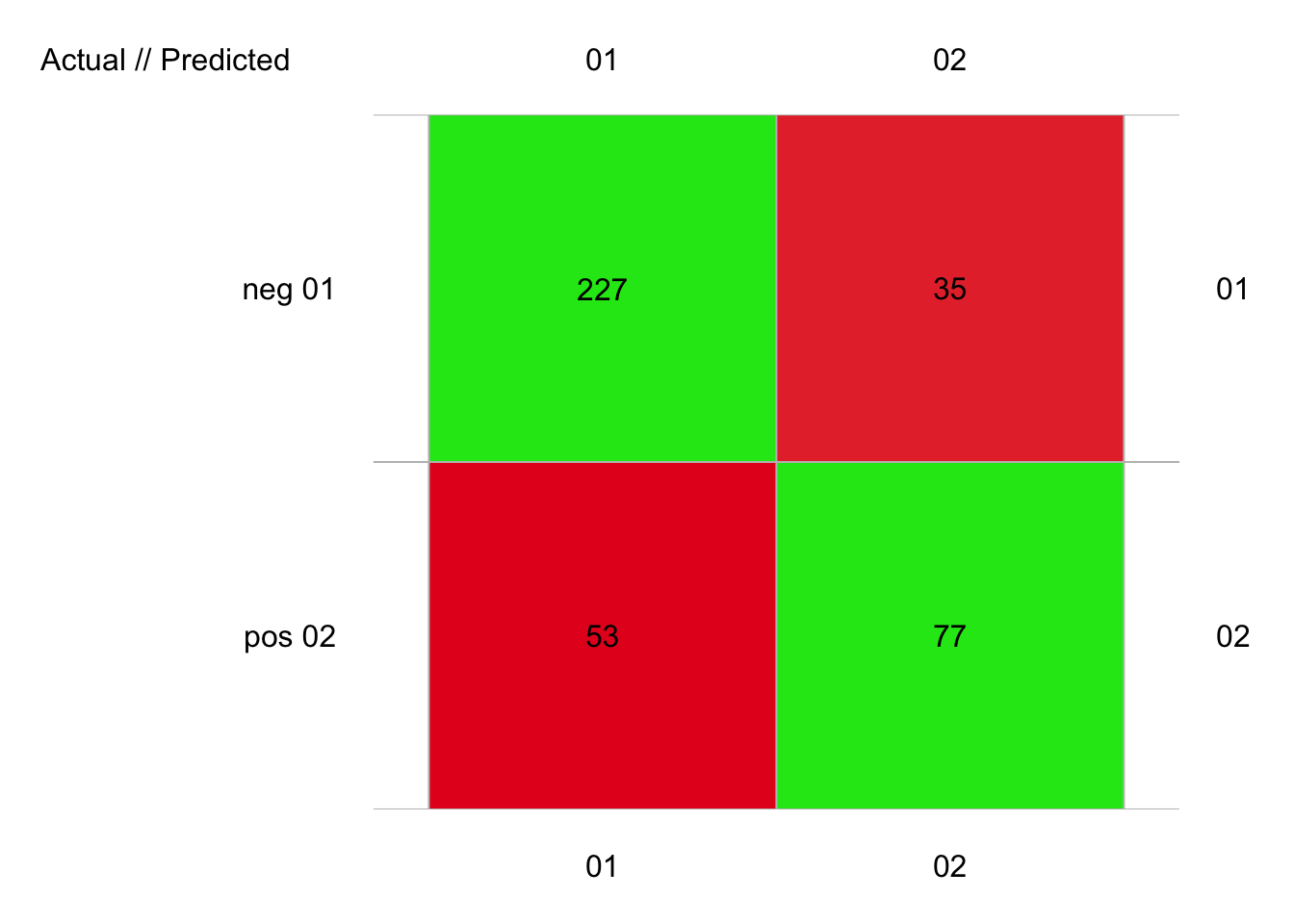
# 392 items classified with 304 true positives (error = 22.4%)
#
# Global statistics on reweighted data:
# Error rate: 22.4%, F(micro-average): 0.739, F(macro-average): 0.737
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8376384 0.8664122 0.8107143 0.5923077 0.6875000 0.4076923 0.1335878
# pos 0.6363636 0.5923077 0.6875000 0.8664122 0.8107143 0.1335878 0.4076923
# FDR FOR LRPT LRNT LRPS LRNS BalAcc MCC
# neg 0.1892857 0.3125000 2.125162 0.2255378 2.594286 0.2753247 0.72936 0.4780594
# pos 0.3125000 0.1892857 4.433846 0.4705524 3.632075 0.3854626 0.72936 0.4780594
# Chisq Bray Auto Manu A_M TP FP FN TN
# neg 89.588 0.02295918 280 262 18 227 53 35 77
# pos 89.588 0.02295918 112 130 -18 77 35 53 227Nous avons ici un peu plus de 22% d’erreur, soit le meilleur score de peu devant l’ADL. Notons que le temps de calcul est déjà non négligeable sur ce petit jeu de données (faire attention à de très gros jeux de données avec cette méthode).
library(mlearning)
pima2_rf <- mlRforest(data = pima2, diabetes ~ .)
set.seed(9764)
pima2_rf_conf <- confusion(cvpredict(pima2_rf, cv.k = 10), pima2$diabetes)
plot(pima2_rf_conf)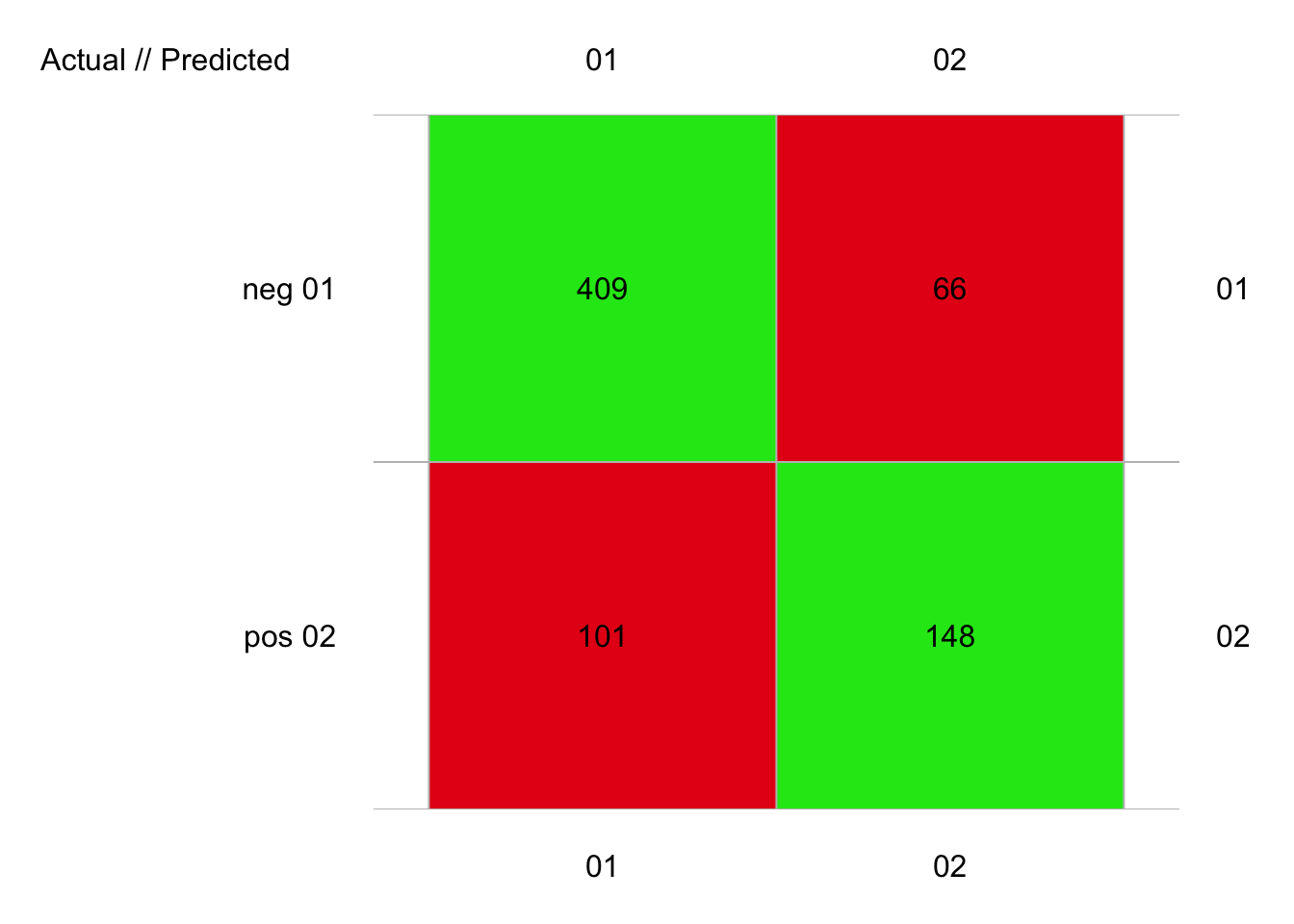
# 724 items classified with 557 true positives (error = 23.1%)
#
# Global statistics on reweighted data:
# Error rate: 23.1%, F(micro-average): 0.737, F(macro-average): 0.735
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8304569 0.8610526 0.8019608 0.5943775 0.6915888 0.4056225 0.1389474
# pos 0.6393089 0.5943775 0.6915888 0.8610526 0.8019608 0.1389474 0.4056225
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.1980392 0.3084112 2.122793 0.2337696 2.600297 0.2863540 0.7277151
# pos 0.3084112 0.1980392 4.277717 0.4710775 3.492181 0.3845714 0.7277151
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.4741069 162.7388 0.02417127 510 475 35 409 101 66 148
# pos 0.4741069 162.7388 0.02417127 214 249 -35 148 66 101 409Avec 23% d’erreur, nous avons encore une fois le meilleur algorithme. Nous pouvons encore effectuer deux choses à partir d’ici : (1) optimiser les paramètres, et (2) étudier l’importance des variables dans la classification. Concernant le nombre d’arbres, un graphique montre la variation de l’erreur en fonction du nombre d’arbres dans notre forêt.
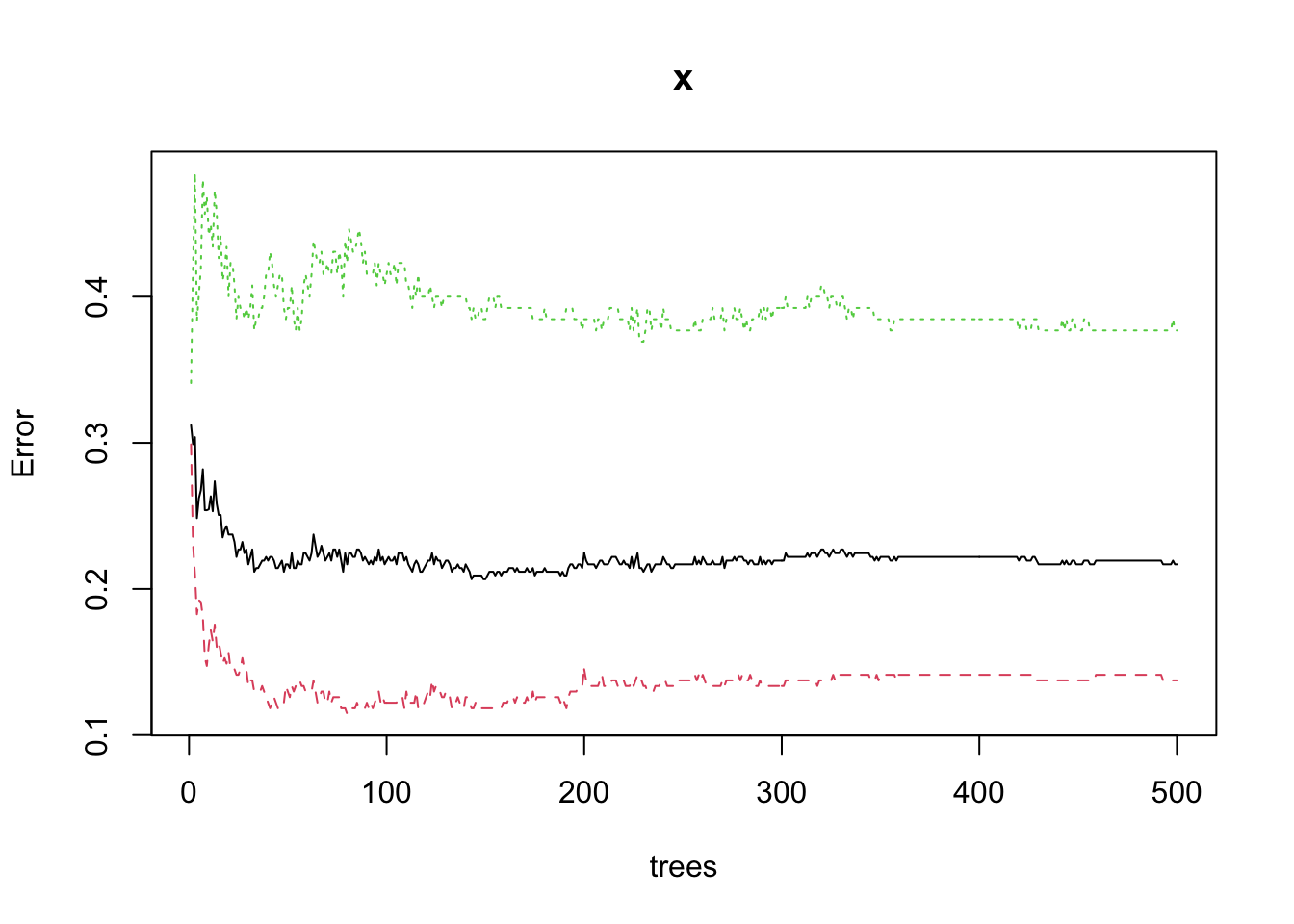
Comme il y a très clairement un aspect probabiliste ici, le graphique indique les erreurs minimales et maximales observées en rouge et en vert, respectivement. En noir, la tendance générale. Nous voyons qu’avec quelques arbres, l’erreur est plus importante, mais elle diminue ici rapidement pour se stabiliser vers les 200 arbres. Donc, si nous voulons gagner du temps de calcul sans perdre en performance, nous pourrions définir ici ntree = 200 dans mlRforest(). différentes valeurs pour l’argument mtry() pourraient aussi parfaitement être étudiées, mais en pratique, la valeur par défaut donne bien souvent déjà les meilleurs résultats.
Un autre graphique présente l’importance des variables : varImpPlot() du package {randomForest}.
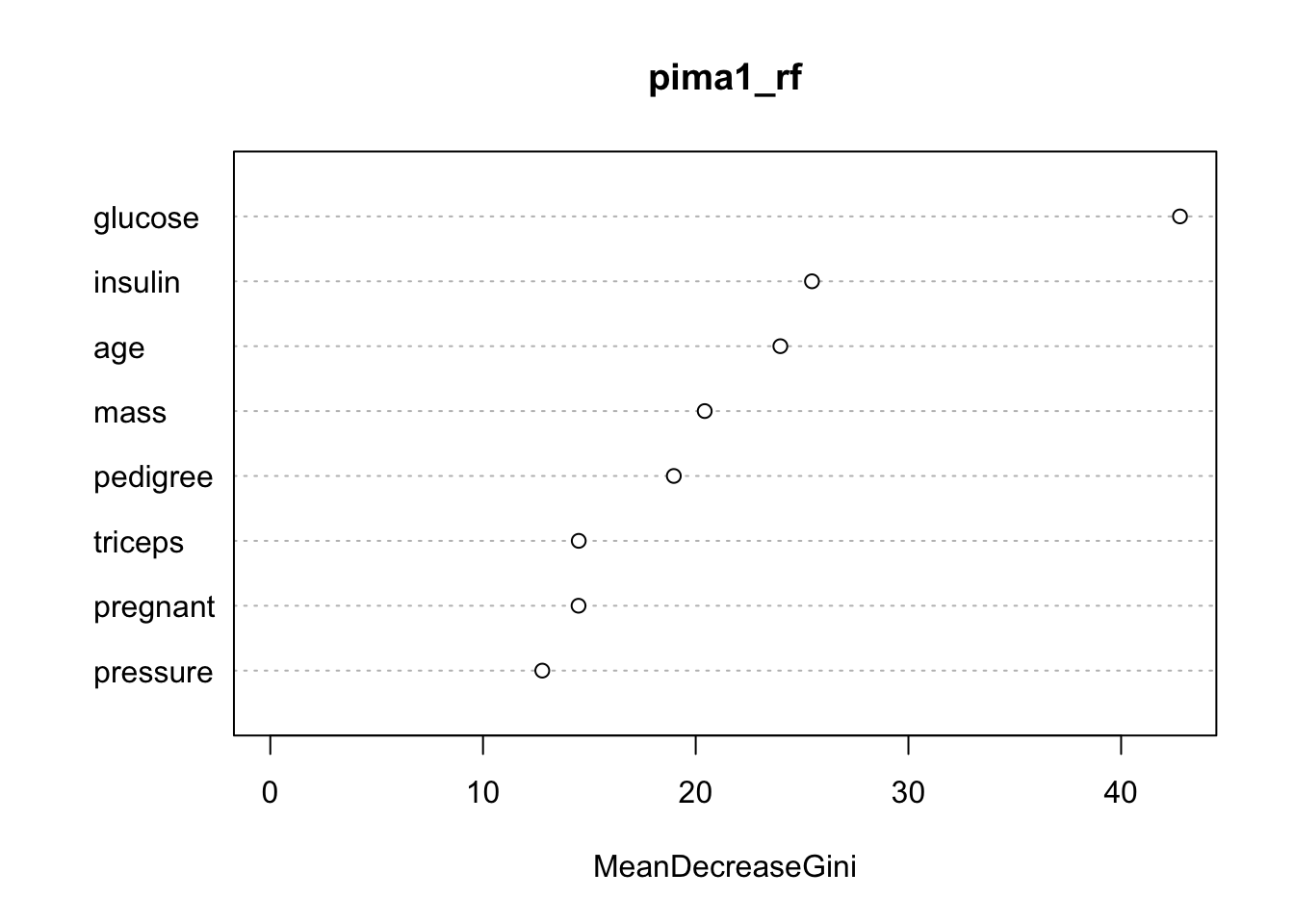
Le critère utilisé est la diminution de l’indice Gini à chaque fois que la variable en question apparaît à un nœud d’un des arbres de la forêt. L’indice Gini pour une probabilité p est p(p - 1). Plus les probabilités s’éloignent de 0,5, plus l’indice est petit. Appliqué à la proportions d’items par classe, plus les sous-groupes résultant d’une division dans l’arbre sont purs, plus la probabilité d’une classe s’approche de 1 tandis que celle des autres tend vers zéro… et donc l’indice Gini diminue. Donc, la variable qui a le plus contribuer à diminuer Gini est aussi celle qui est la plus discriminante entre les classes, ici c’est clairement glucose, suivi de insulin et age. Par contre, triceps, pregnant et pressure ont moindre importance, bien que celle-ci ne soit pas complètement nulle.
Sur cette base, nous pourrions décider de simplifier notre modèle en laissant tomber, par exemple, les trois dernières variables de moindre importance et en se limitant à 200 arbres.
library(mlearning)
pima1_rf2 <- mlRforest(data = pima1, diabetes ~ glucose + insulin + age + mass + pedigree,
ntree = 200)
set.seed(85436)
pima1_rf2_conf <- confusion(cvpredict(pima1_rf2, cv.k = 10), pima1$diabetes)
plot(pima1_rf2_conf)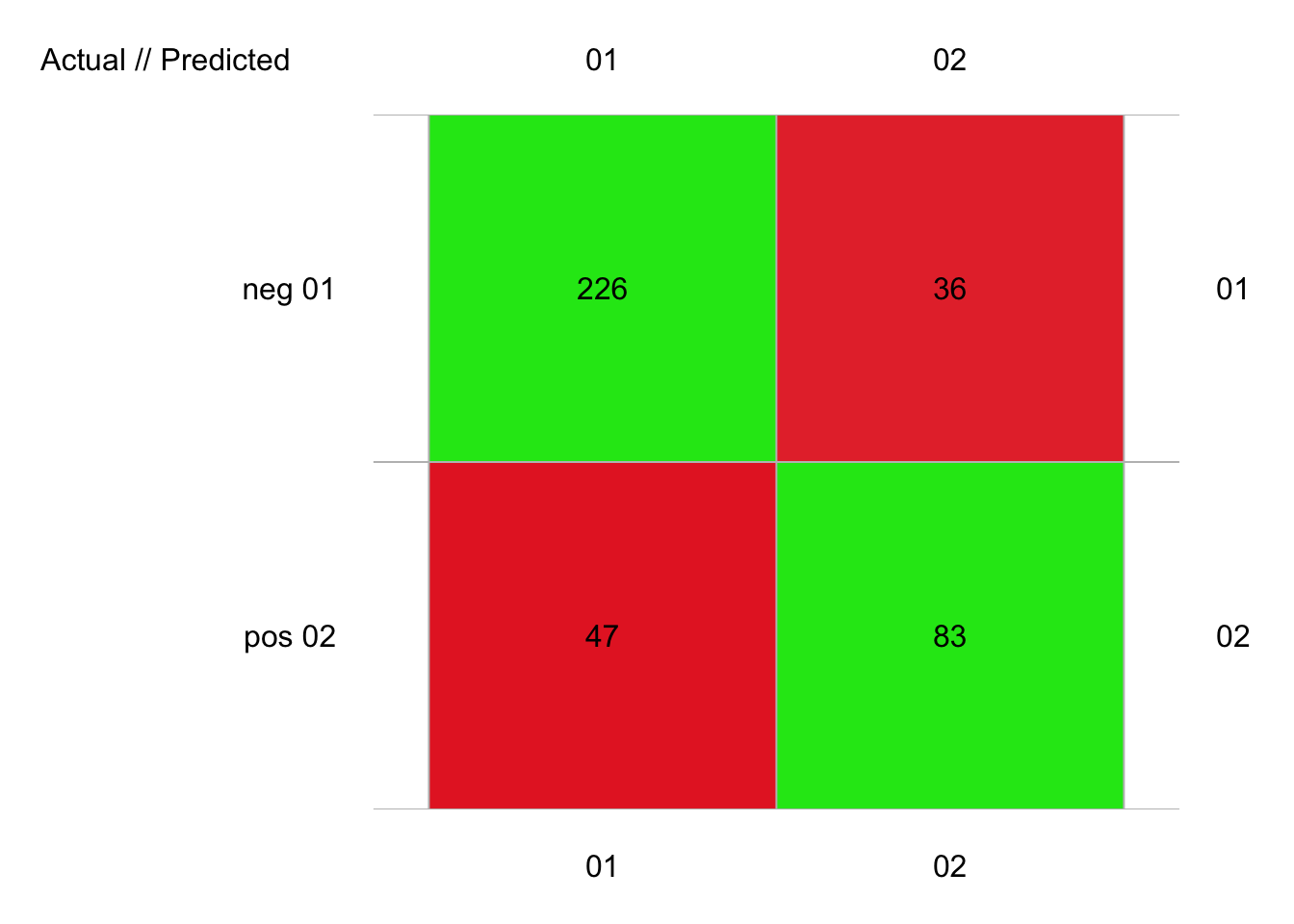
# 392 items classified with 309 true positives (error = 21.2%)
#
# Global statistics on reweighted data:
# Error rate: 21.2%, F(micro-average): 0.757, F(macro-average): 0.756
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8448598 0.8625954 0.8278388 0.6384615 0.6974790 0.3615385 0.1374046
# pos 0.6666667 0.6384615 0.6974790 0.8625954 0.8278388 0.1374046 0.3615385
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.1721612 0.3025210 2.385902 0.2152120 2.736467 0.2468335 0.7505285
# pos 0.3025210 0.1721612 4.646581 0.4191287 4.051314 0.3654347 0.7505285
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.513044 103.1799 0.01403061 273 262 11 226 47 36 83
# pos 0.513044 103.1799 0.01403061 119 130 -11 83 36 47 226Effectivement, avec un petit peu plus de 21%, c’est notre meilleur score jusqu’ici, tout en réduisant le nombre d’attributs nécessaires et d’arbres à calculer. Dans le module suivant, nous étudierons encore quelques concepts autour de la classification supervisée afin de réaliser un choix éclairé du meilleur modèle.
À vous de jouer !
Réalisez le travail C02Ia_ml2, partie III.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2021-12-24 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md, partie III.
Trucs et astuces
Pour l’instant {mlearning} utilise les fonctions du package {randomForest} qui reprend le code original de Breiman. Cependant, d’autres implémentations plus performantes ont été développées depuis. En particulier, le package R {ranger} implémente une version parallélisée (utilisation de plusieurs cœurs du processeur pour effectuer le calcul en parallèle) bien plus rapide sur les ordinateur actuels. Si la vitesse est un frein à l’utilisation de la forêt aléatoire dans votre application, allez voir du côté de cette implémentation.