5.4 Décomposition par LOESS
LOESS (prononcez “LO-ESSE”) est une méthode de régression polynomiale locale. Pour chaque valeur \(X_t\) d’une série \(X\), on va considérer les k voisins à gauche et à droite, éventuellement pondérés (par exemple par la distance les séparant de \(X_t\)). On effectue une régression par les moindres carrés d’un polynôme d’ordre p (habituellement p vaut 1 ou 2), et on récupère la valeur prédite au temps \(t\) (voir Cleveland et al, 1992). Il s’agit donc de l’utilisation d’une régression polynomiale dans une fenêtre mobile. Si l’ordre p du polynôme vaut 0, le calcul se ramène à une moyenne mobile classique.
Avec un choix judicieux de k, et éventuellement en réitérant le processus, on va pouvoir extraire la tendance générale. Comme avec la méthode des moyennes mobiles, on va aussi pouvoir désaisonnaliser une série en prenant une fenêtre égale à un an, donc, en considérant 12 termes pour des données mensuelles (13 en fait pour une fenêtre centrée sur les observations de la série). Une combinaison de ces deux traitements va permettre de décomposer une série en tendance, cycle saisonnier et résidus selon un modèle additif. On peut aussi n’extraire que le cycle saisonnier et les résidus (surtout utile lorsque la tendance générale est périodique sur un an).
Comme les résidus ont rarement une distribution normale et ne sont souvent pas indépendants entre eux dans les séries, les hypothèses de base indispensables pour la régression à l’aide de la méthode des moindres carrés sont violées la plupart du temps. Ainsi, pour obtenir une estimation plus exacte des composantes, il est possible d’utiliser une méthode de régression plus robuste (i.e., moins sensible à la violation de ces hypothèses de base). On peut par exemple décider de pondérer les valeurs de manière inversement proportionnelle à leur influence respective sur la régression. Ainsi, une valeur qui, à elle seule, aurait tendance à tirer la courbe vers elle (valeur isolée, très éloignée du nuage formé par toutes les autres) recevra une pondération très faible afin de minimiser son effet.
L’algorithme implémenté dans decloess() ou tsd(method = "loess"), lui-même implémenté dans stl() est en réalité un peu plus complexe, avec des passages multiples des différents filtres dans un ordre particulier, et avec un calcul supplémentaire éventuellement entre ces passages. Ceci explique que la méthode est plus efficace qu’une simple moyenne mobile. Cependant, les explications ci-dessus suffisent pour en comprendre le principe général. Si vous êtes intéressés par les détails, vous pouvez lire la page d’aide de ?stl.
Exemple
Le jeu de données qui se prête merveilleusement bien à la décomposition LOESS est co2. Nous l’avons déjà réalisée. Néanmoins, nous la reprenons ici pour discuter de différentes valeurs possibles des arguments qui vont influer sur la forme des différentes composantes extraites.
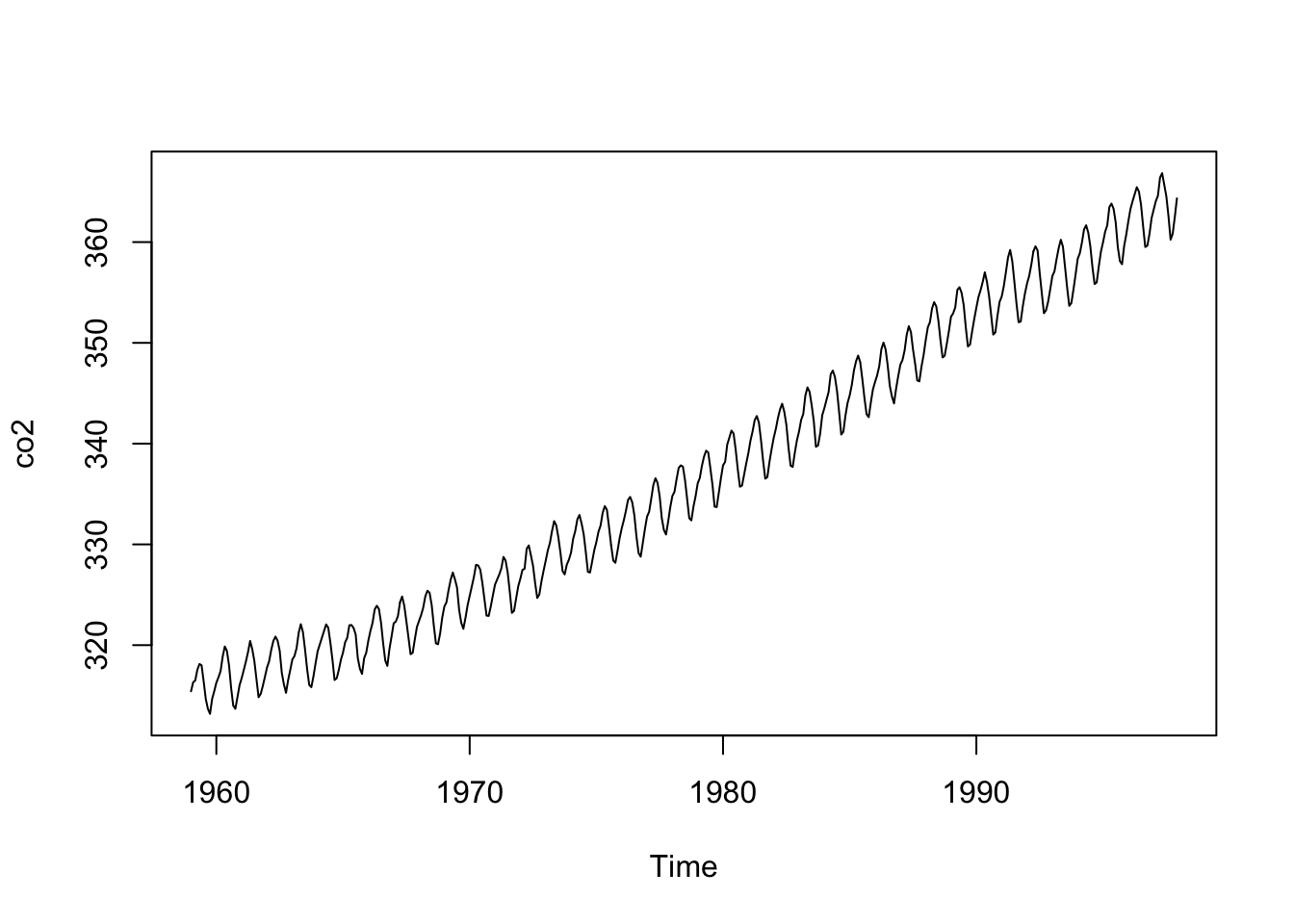
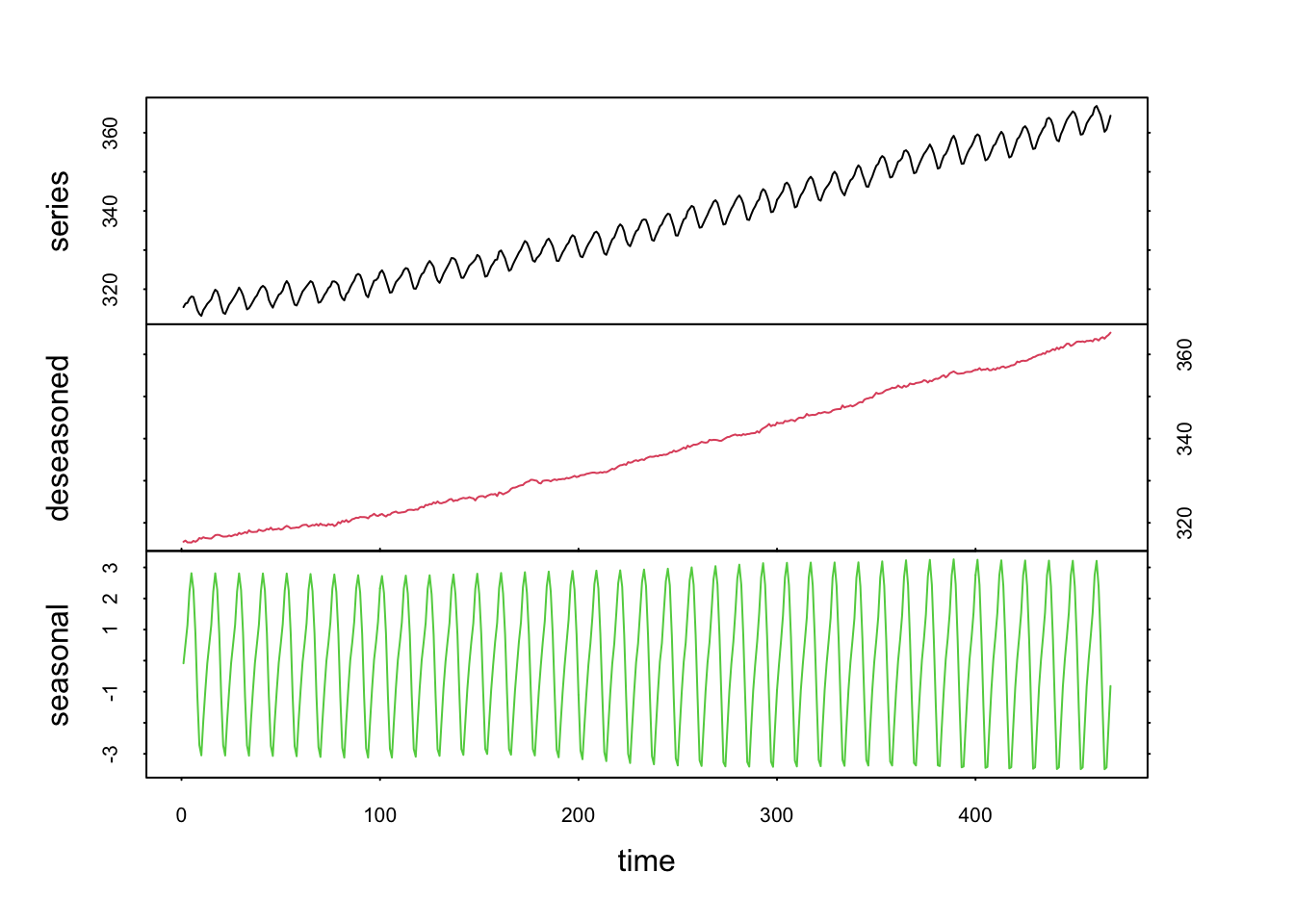
L’argument s.window = n’a pas de valeur par défaut et doit donc être toujours fourni. Il s’agit de l’étendue de la fenêtre de décomposition saisonnière (attention : l’étendue est bien 2 k + 1, où k est l’argument order = pour les moyennes mobiles). Nous choisissons la valeur impaire immédiatement supérieure à la fréquence des observations pour une unité d’un an (ou d’un cycle, en tous cas). Donc, pour des données mensuelles, s.window = 13. Une autre valeur possible est s.window = "periodic". Dans ce cas, la valeur moyenne à chaque mois sera calculée sur toute la longueur de la série. Il en résulte un signal cyclique de forme quelconque, mais strictement identique chaque année :
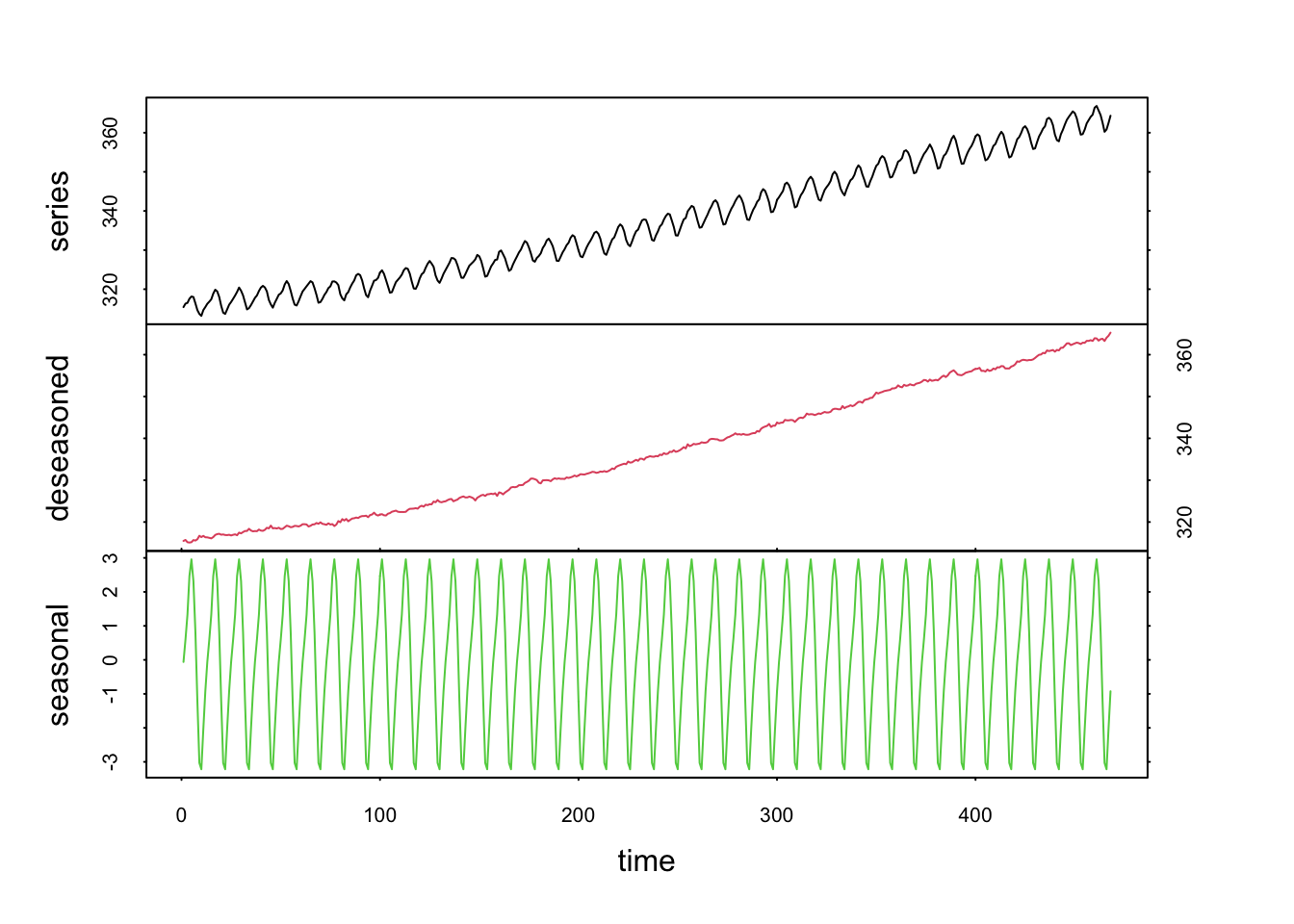
L’argument s.degree = indique le degré du polynôme utilisé pour l’extraction de la composante saisonnière. Il peut valoir zéro (valeur par défaut pour utiliser les moyennes mobiles). Donc, notre première décomposition en n’indiquant que s.window = 13 se rapproche en fait à l’application d’un lissage par moyenne mobile. Lorsque s.degree = 1, nous ajustons une droite par les moindres carrés à chaque fois dans le fenêtre. Le signal résultant est très légèrement différent (non perceptible ici).
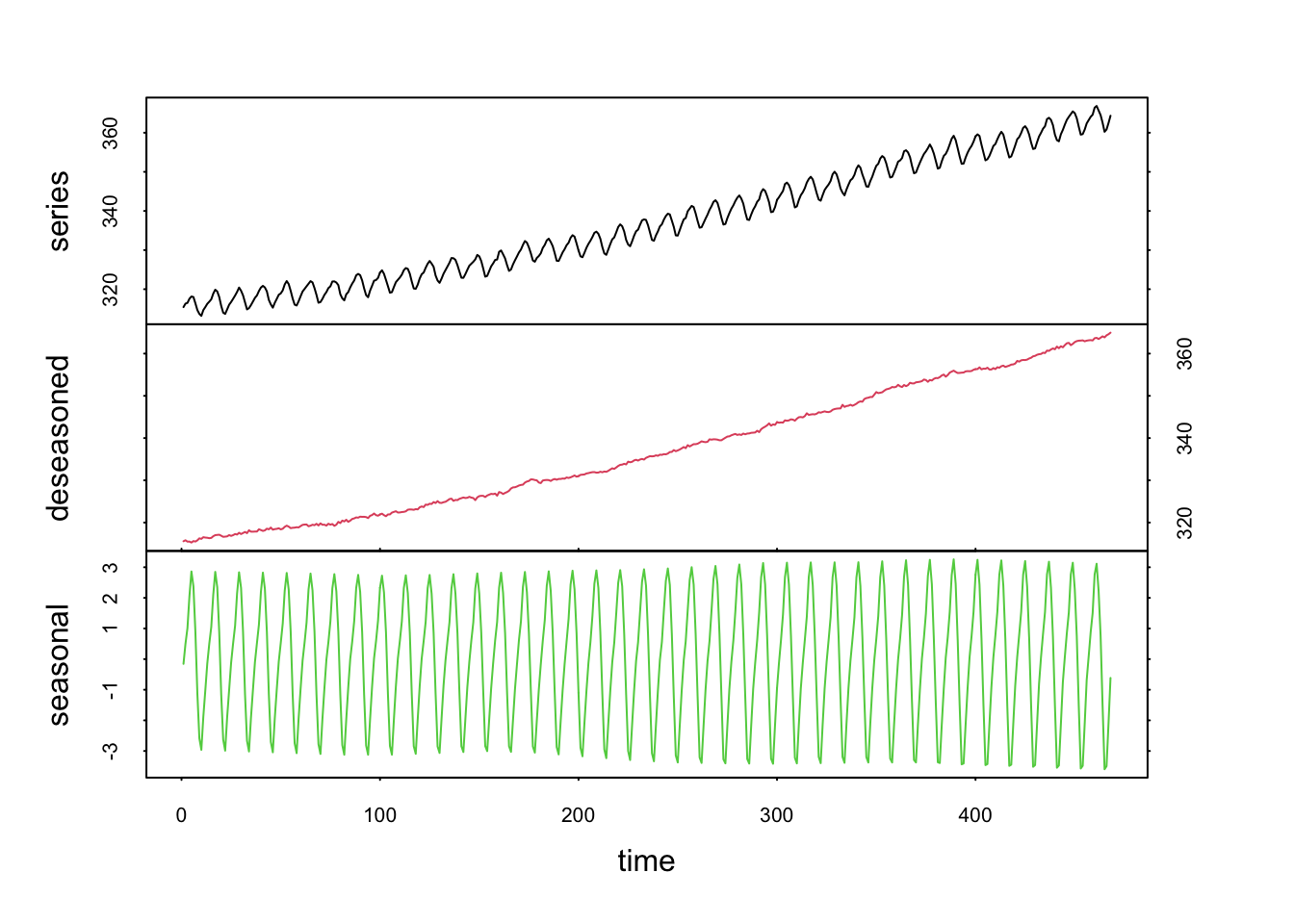
L’argument trend = indique si nous désaisonnalisons uniquement ou si nous retirons également une tendance générale. La valeur par défaut est trend = FALSE. Si nous indiquons trend = TRUE, la fonction utilise des valeurs par défaut pour t.window =, la largeur de la fenêtre pour l’extraction de la tendance (voir ?stl pour l’explication plus détaillée et pour le calcul de la valeur pas défaut). Enfin, t.degree = 1 par défaut, mais il peut aussi être ramené à zéro. Cette dernière valeur est moins intéressante dans le cas de la tendance bien souvent.
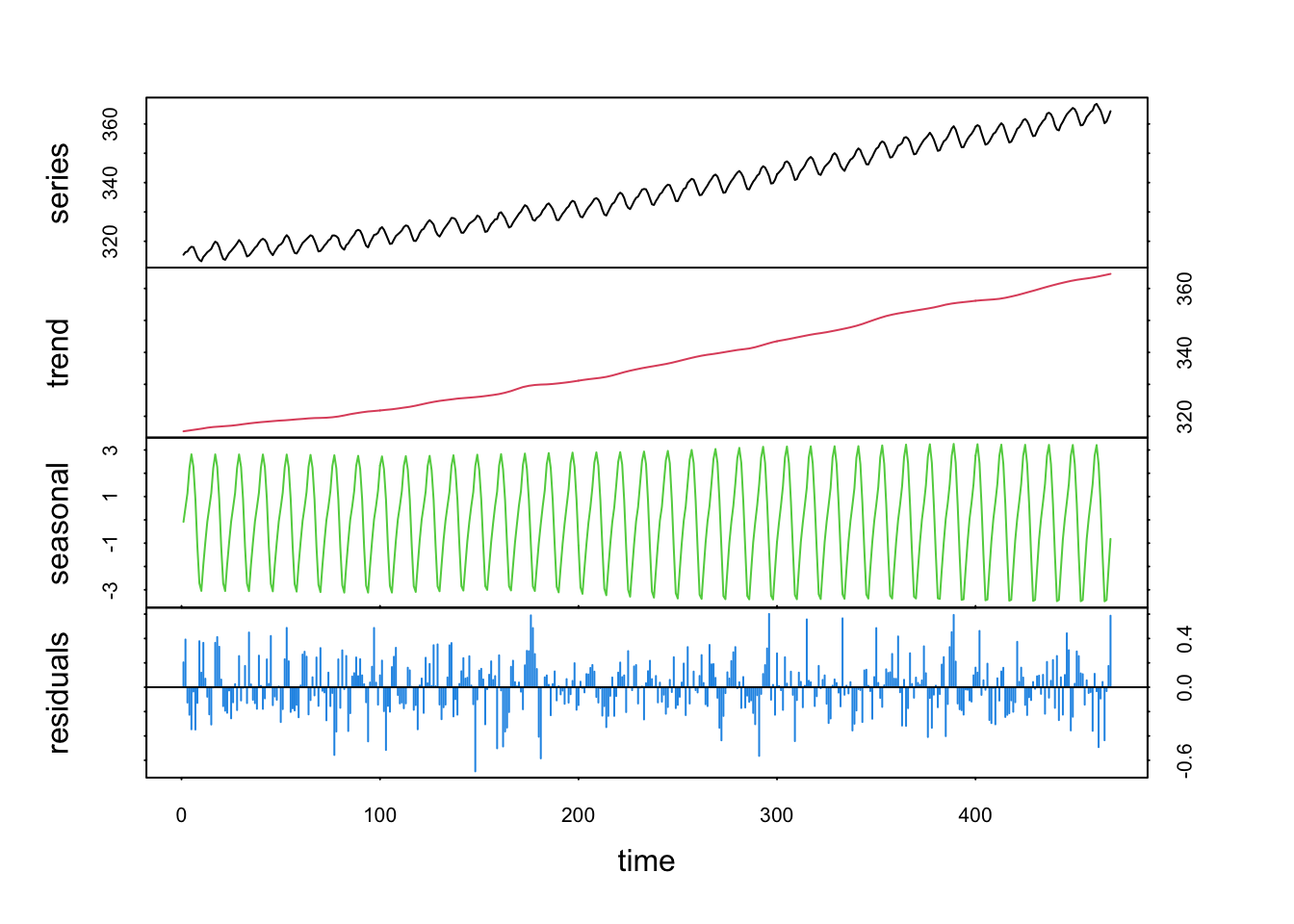
Si nous diminuons la valeur de t.window =, la tendance générale est moins lissée. La plupart du temps, les valeurs par défaut conviennent très bien.
co2_loess <- tsd(co2, method = "loess", s.window = 13, trend = TRUE, t.window = 7)
plot(co2_loess, col = 1:4)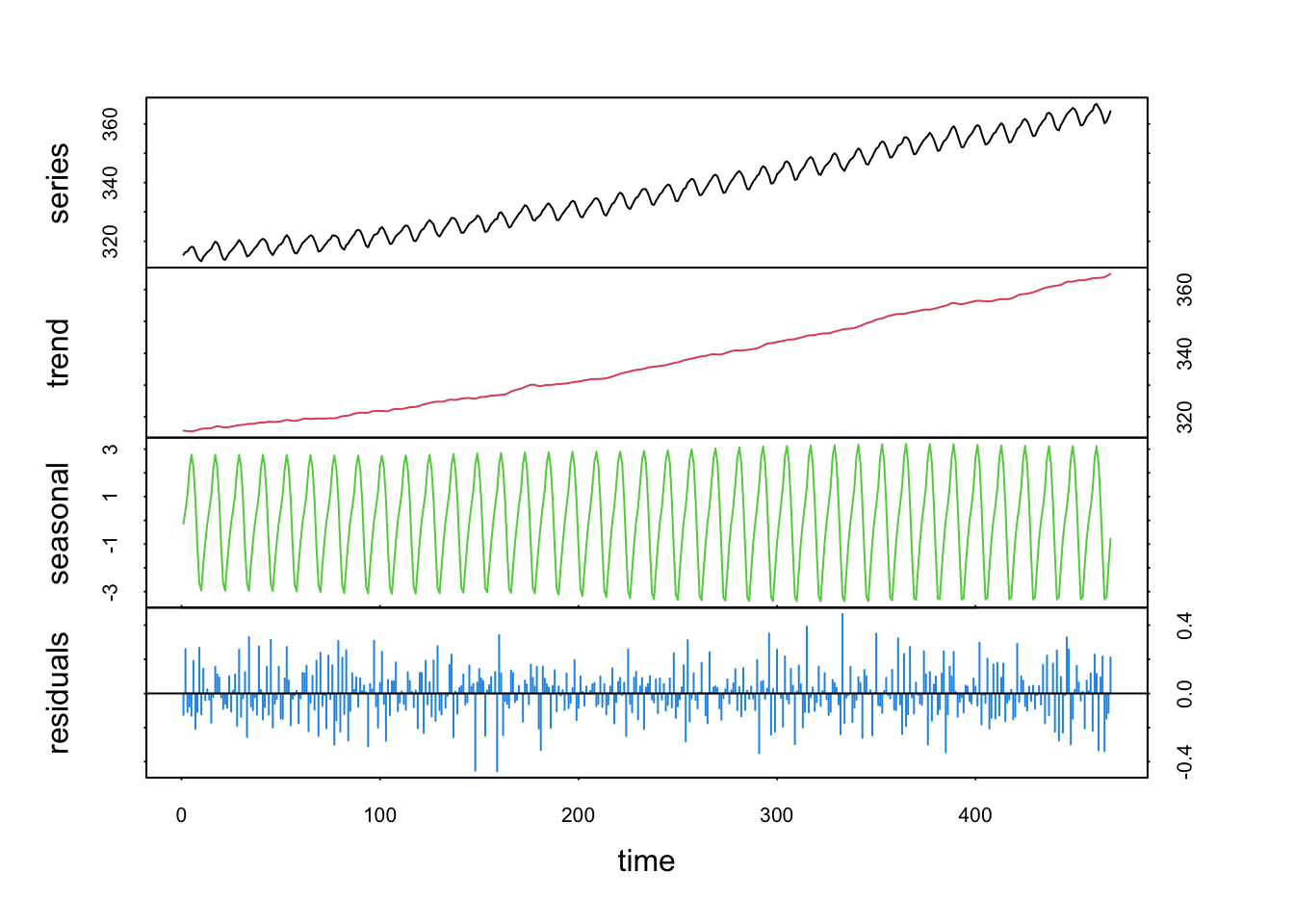
Enfin, en présence de valeurs extrêmes suspectes, nous pouvons utiliser une régression robuste à la place d’une régression par les moindres carrés classiques. Il suffit pour cela de préciser robust = TRUE (pas nécessaire ici).
co2_loess <- tsd(co2, method = "loess", s.window = 13, trend = TRUE, robust = TRUE)
plot(co2_loess, col = 1:4)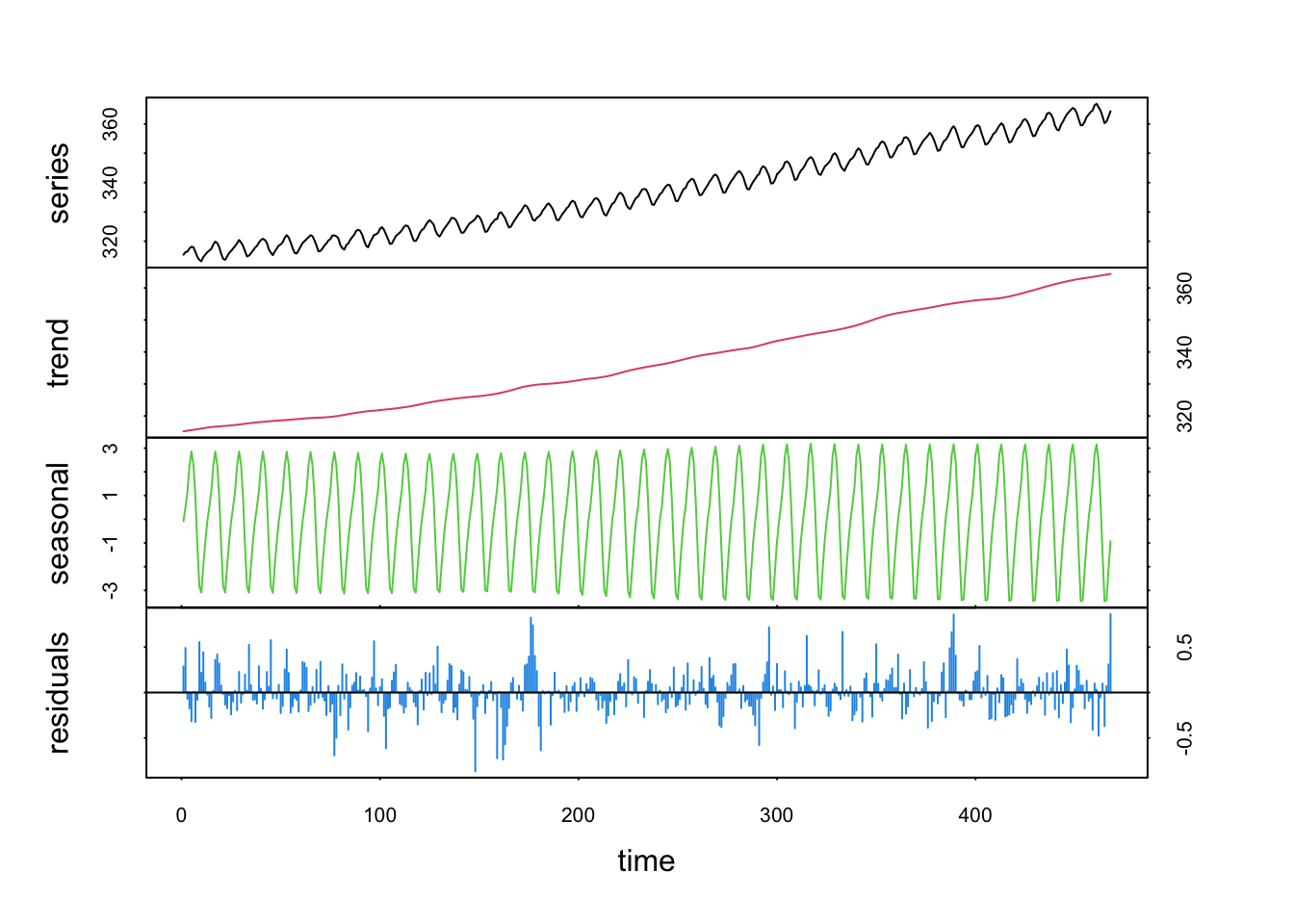
Enfin, terminons en signalant que si la méthode est prévue pour traiter uniquement des modèles additifs, decloess() et tsd(method = "loess") sont également capables de traiter des modèles multiplicatifs avec type = "multiplicative" grâce à l’astuce de la transformation logarithmique du signal implémentée en interne dans ces fonctions, mais stl(), elle ne le peut pas.
À vous de jouer !
Réalisez en groupe le travail C05Gb_ts_adv.
Travail en groupe de 2 pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2021-10-08 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md.