5.3 Régressions et séries
Les régressions linéaires et non linéaires, surtout s’il s’agit de modèles ajustés par les moindres carrés, ne sont a priori pas compatibles avec les séries spatio-temporelles puisqu’elles nécessitent une indépendance des observation, une distribution Normale des résidus, etc. Mais en fait toutes ces conditions s’appliquent aux tests d’hypothèses autour de le régression. Si nous nous contentons d’utiliser la régression pour estimer la forme d’une composante, et ensuite que nous l’extrayons sans utiliser le tableau de l’ANOVA, les tests de Student sur les paramètres, etc., alors notre usage de cet outil sera approprié ici.
5.3.1 Estimation de la tendance par régression
Les méthodes de filtrage présentées ci-dessus permettent d’extraire ou d’éliminer une tendance de forme quelconque (on n’a pas d’idée a priori de sa forme ; on ne cherche pas à la modéliser). Les méthodes d’estimation par régression, au contraire, font appel à des hypothèses très fortes quant à sa nature : on cherche à ajuster une ou plusieurs équations fonctionnelles à la tendance de la série.
5.3.1.1 Tendance générale
L’idée simple pour estimer une tendance générale est de vérifier son ajustement par une droite, une parabole, un polynôme d’ordre plus élevé simulant un mouvement pseudo-cyclique de forte période. Ces techniques reposent sur l’algorithme des moindres carrés : on minimise les carrés d’écarts entre les données observées et un polynôme de degré fixé à l’avance.
On pourrait imaginer bien d’autres formes de tendance générale (exponentielle, logistique, etc.). Certains de ces modèles prennent même en compte une autocorrélation entre les observations, aspect fondamental dans le cadre de l’analyse de séries spatio-temporelles. Ces modèles autorégressifs sont très importants dans le domaine, mais ils sont plutôt appliqués en économie, en physique, … et moins en biologie. Nous ne les étudierons donc pas ici.
Exemple
Nous reprenons ici l’exemple du manuel de {pastecs} qui illustre bien l’utilisation de différents modèles (linéaire, polynomial, non linéaire) pour estimer la tendance générale de la densité de l’eau le long du transect Nice - Calvi pour le jeu de données marphy (comme c’est un excès de densité par rapport à 1000 g/L qui est enregistrée dans le jeu de données, nous rajoutons 1000 pour rétablir la valeur).
data("marphy", package = "pastecs")
density <- ts(marphy$Density + 1000)
plot(density, xlab = "Transect Nice - Calvi (stations)",
ylab = "Densité [g/L]")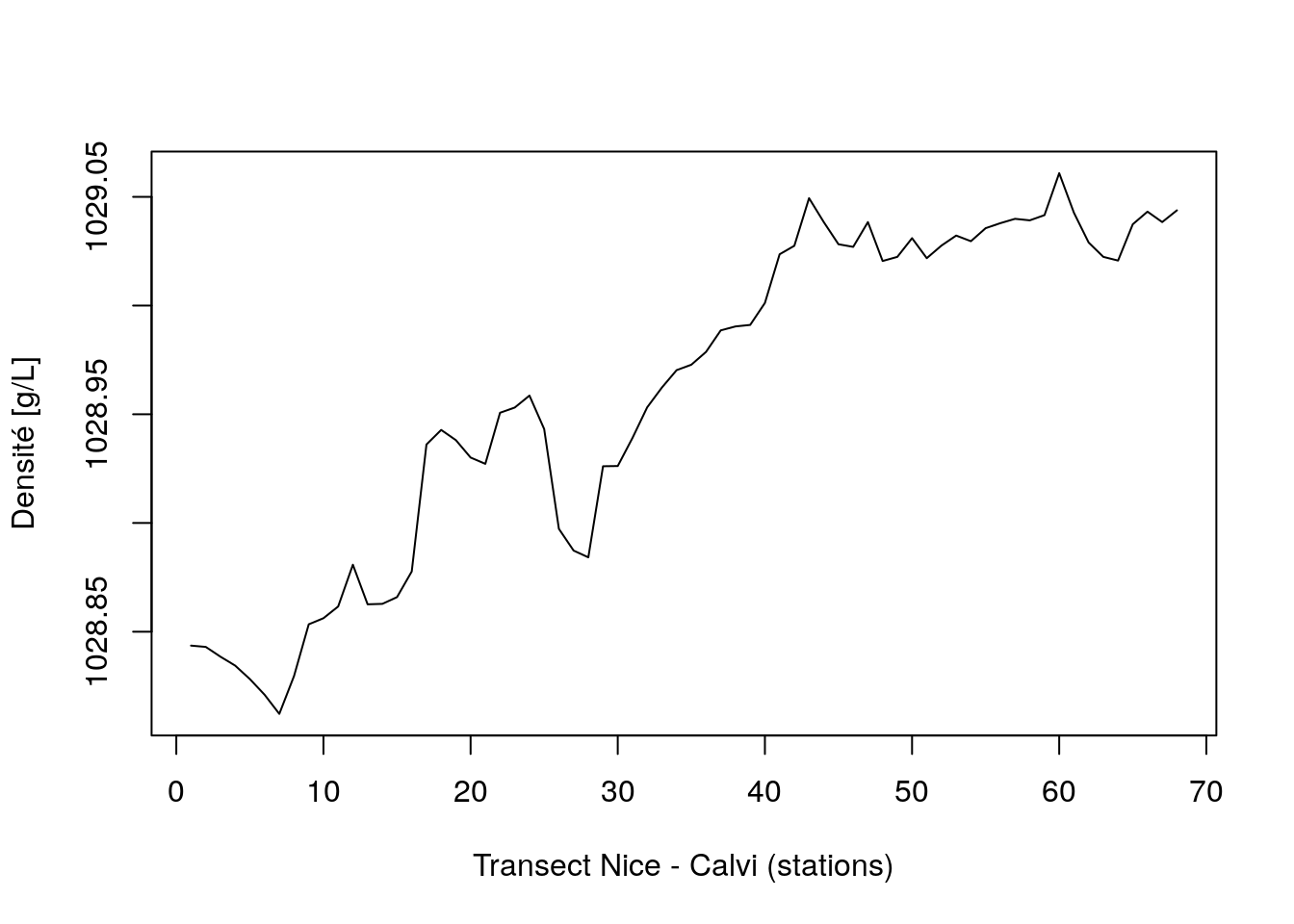
Nous voyons très bien ici une nette tendance à l’augmentation. Ajustons tout d’abord une simple droite pour estimer (et extraire) la tendance générale :
library(pastecs)
t <- time(density) # Extraction du vecteur temps de l'objet ts
density_lin <- lm(density ~ t) # Ajustement
coef(density_lin) # Paramètres du modèle ajusté# (Intercept) t
# 1.028835e+03 3.605243e-03Remarquons que nous avons appelé lm() ici sans préciser data =. Dans ce cas, la fonction va rechercher ses variables comme vecteurs numériques directement dans l’environnement de travail. Nous avions déjà density qui est un objet ts, mais nous savons par ailleurs que ce ts est aussi, et avant tout, un vecteur numérique (auquel un attribut tsp a été ajouté, attribut inconnu et donc ignoré de lm()). Nous avons créé notre second vecteur numérique t en extrayant la variable de temps de l’objet ts en utilisant time(). Ainsi, nous pouvons travailer avec lm() directement.
L’objet density_lin est un objet lm tout-à-fait classique. Nous pouvons donc afficher le tableau summary(), effectuer l’analyse des résidus, etc. et … stop ! Gardez à l’esprit que l’application de lm() à une série temporelle tord le système car la non indépendance des observations entre elles peut être problématique. Nous n’utiliserons donc ici que l’ajustement du modèle sans en analyser les résidus.
#
# Call:
# lm(formula = density ~ t)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.052226 -0.018014 0.001945 0.017672 0.058895
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.029e+03 6.585e-03 156250.31 <2e-16 ***
# t 3.605e-03 1.659e-04 21.73 <2e-16 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.02685 on 66 degrees of freedom
# Multiple R-squared: 0.8774, Adjusted R-squared: 0.8755
# F-statistic: 472.3 on 1 and 66 DF, p-value: < 2.2e-16L’ANOVA, et les tests de Student sur les paramètres ne peuvent être utilisés ici, même si nous pouvons les calculer à partir de summary() ou anova(). Afin d’utiliser ce modèle linéaire pour décomposer la série, nous utilisons predict() pour récupérer les valeurs prédites par le modèle pour la tendance, et nous les utilisons dans decreg() ou tsd(methode = "reg") :
trend_lin <- predict(density_lin)
density_lindec <- tsd(density, method = "reg", xreg = trend_lin)
plot(density_lindec, col = c(1, 3, 2), xlab = "Stations")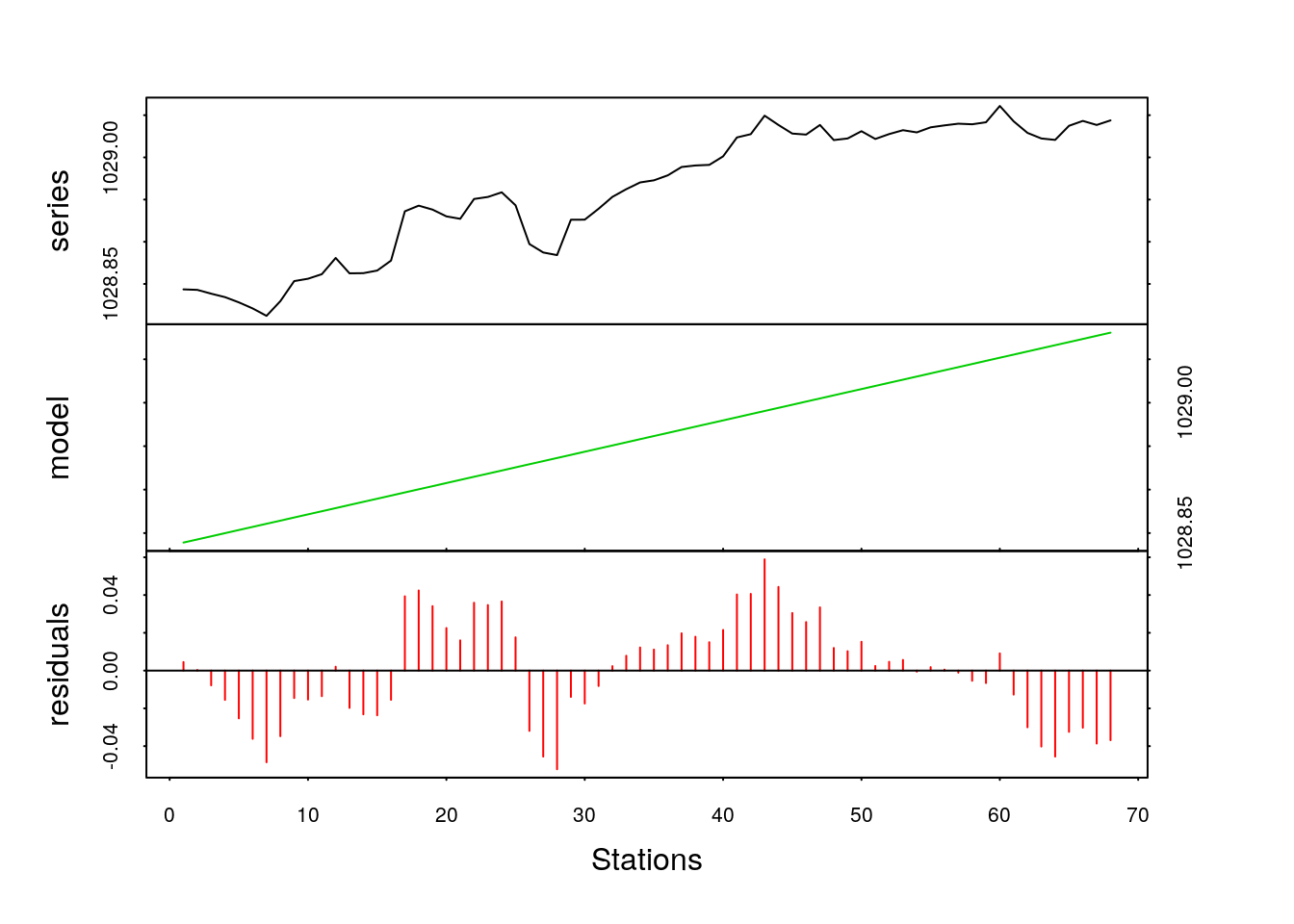
Ou mieux, nous représentons la série de départ et la tendance générale superposée en utilisant stack = FALSE :
plot(density_lindec, stack = FALSE, resid = FALSE, col = c(1, 3),
xlab = "Stations", ylab = "Densité [g/L]", main = "Tendance linéaire")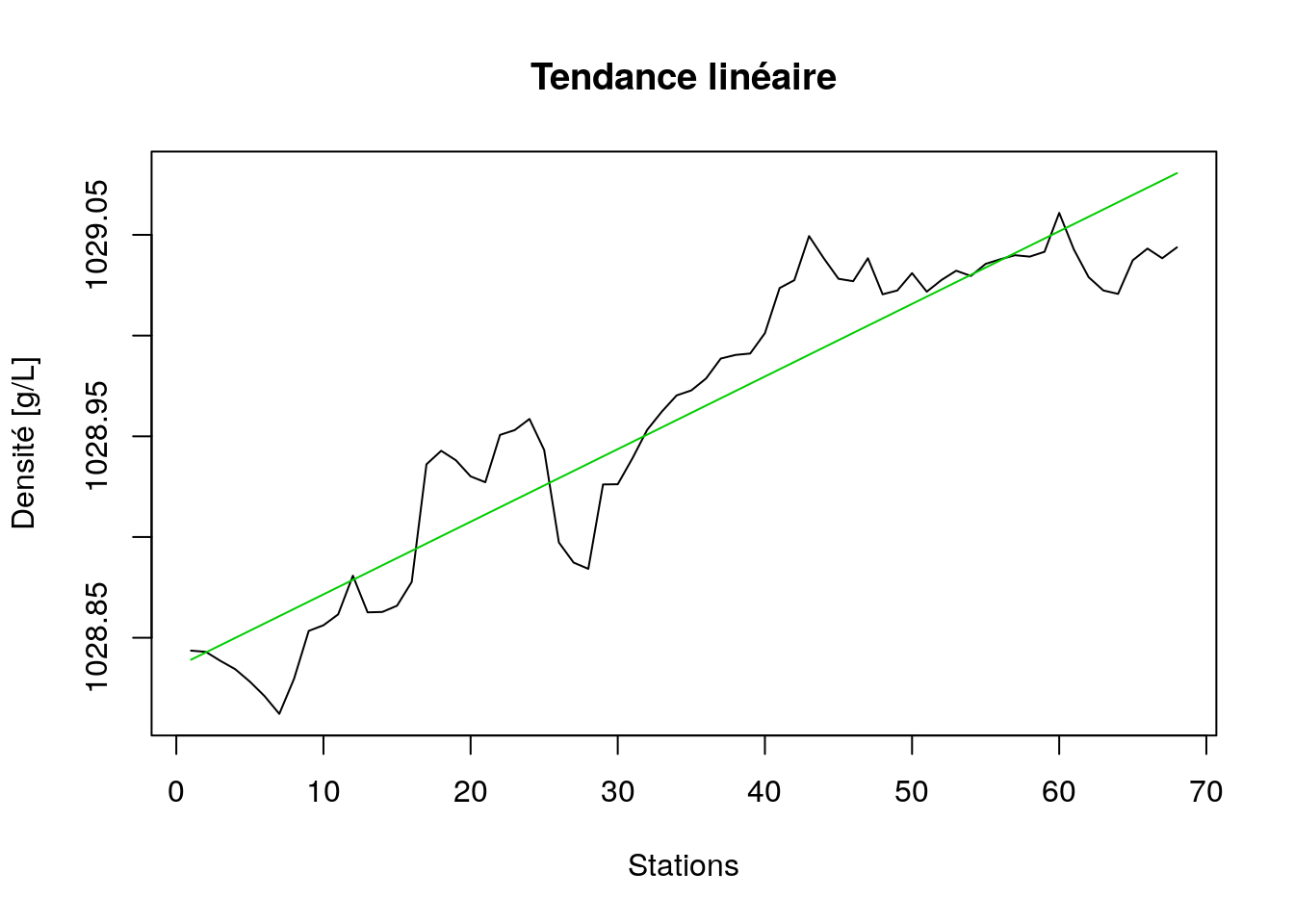
Nous voyons bien que la droite n’est qu’une mauvaise approximation de la tendance générale. Nous pourrions essayer une courbe à la place. Commençons avec un polynôme d’ordre deux.
# (Intercept) t I(t^2)
# 1.028801e+03 6.593172e-03 -4.330333e-05density_poly2dec <- tsd(density, method = "reg", xreg = predict(density_poly2))
plot(density_poly2dec, stack = FALSE, resid = FALSE, col = c(1, 2),
xlab = "Stations", ylab = "Densité [g/L]",
main = "Tendance polynomiale d'ordre 2")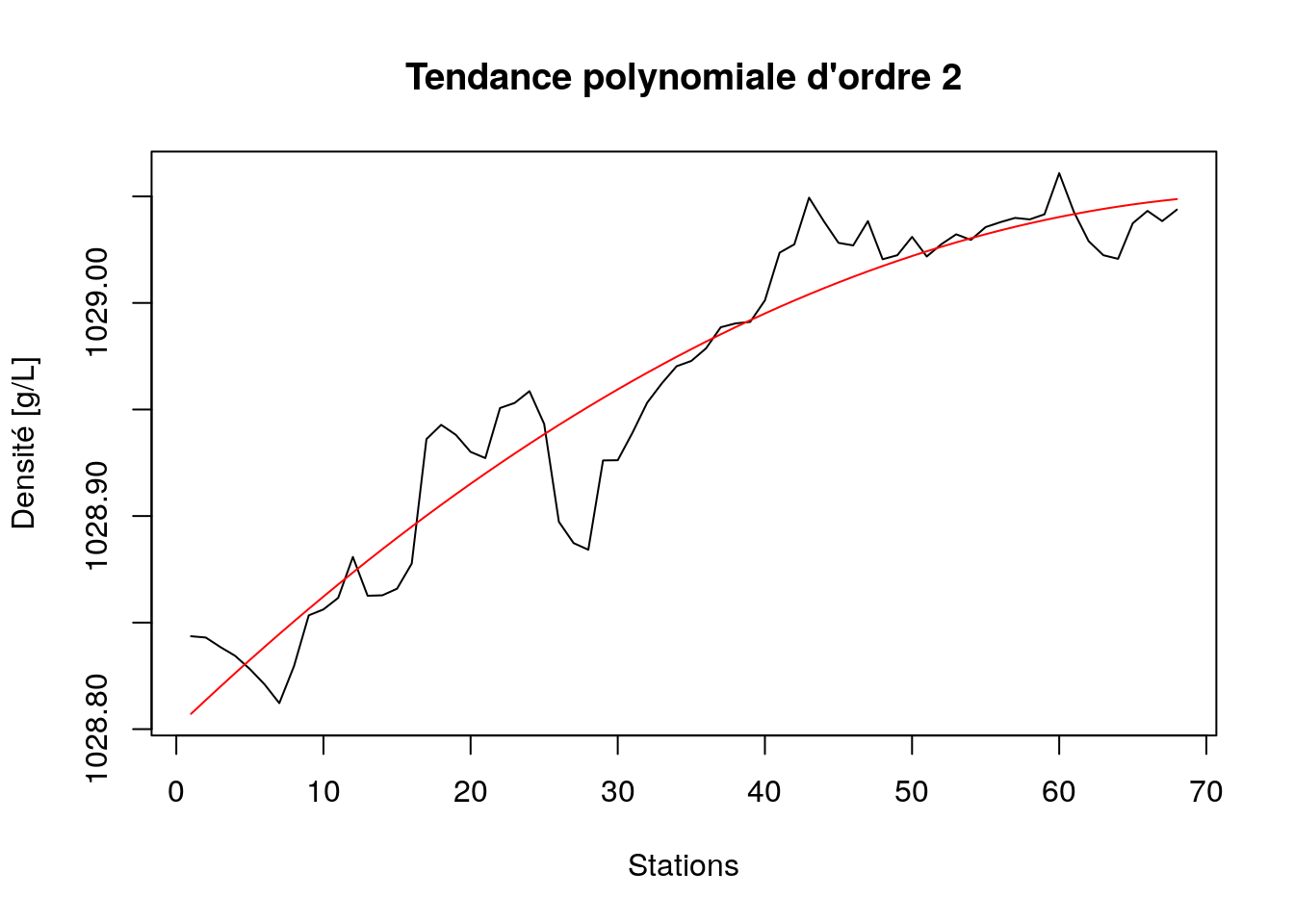
N’oubliez pas d’utiliser I() dans la formule pour indiquer un calcul, sinon, lm() recherchera une variable qui s’appellerait t^2 et ne la trouverait pas bien sûr (et en plus, le message d’erreur n’est pas toujours très explicite dans ce cas). Ce modèle polynomial d’ordre deux est déjà nettement mieux. Et que donne un polynôme d’ordre trois ?
# (Intercept) t I(t^2) I(t^3)
# 1.028822e+03 3.062584e-03 8.368743e-05 -1.226964e-06density_poly3dec <- tsd(density, method = "reg", xreg = predict(density_poly3))
plot(density_poly3dec, stack = FALSE, resid = FALSE, col = c(1, 4),
xlab = "Stations", ylab = "Densité [g/L]",
main = "Tendance polynomiale d'ordre 3")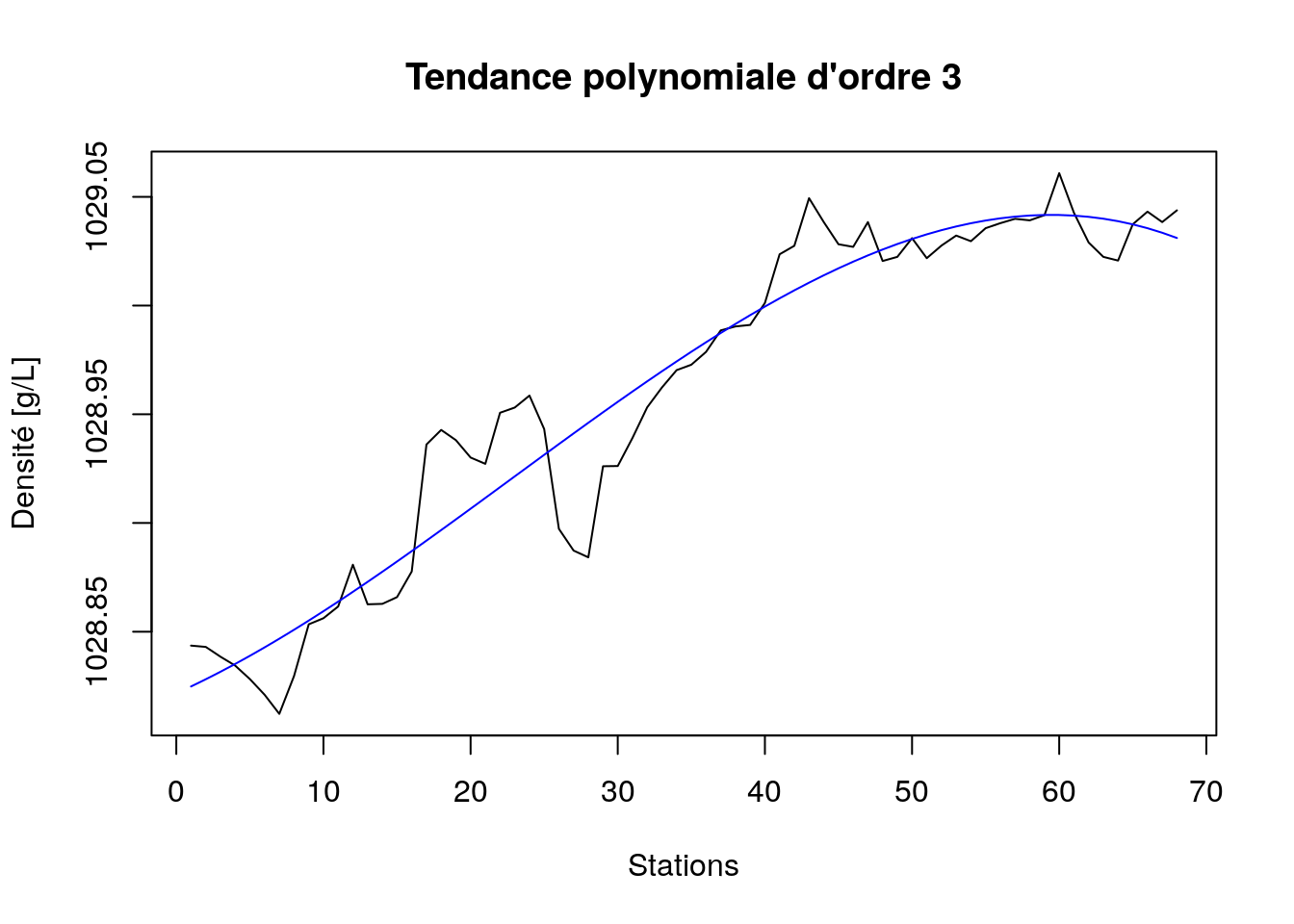
Il ne semble pas que le gain soit flagrant ici… peut-être du côté de la Corse, et encore. Testons à présent une modèle non linéaire. Par exemple, une courbe logistique. Le principe est le même, si ce n’est que nous utilisons ici la fonction nls() à la place de lm() et le modèle SSfpl(..., A, B, xmid, scal) pour le modèle logistique à quatre paramètres (voyez le module 4 du cours SDD II).
# A B xmid scal
# 1028.78310 1029.05367 22.25032 12.85642density_logisdec <- tsd(density, method = "reg", xreg = predict(density_logis))
plot(density_logisdec, stack = FALSE, resid = FALSE, col = c(1, 5),
xlab = "Stations", ylab = "Densité [g/L]",
main = "Tendance logistique à 4 paramètres")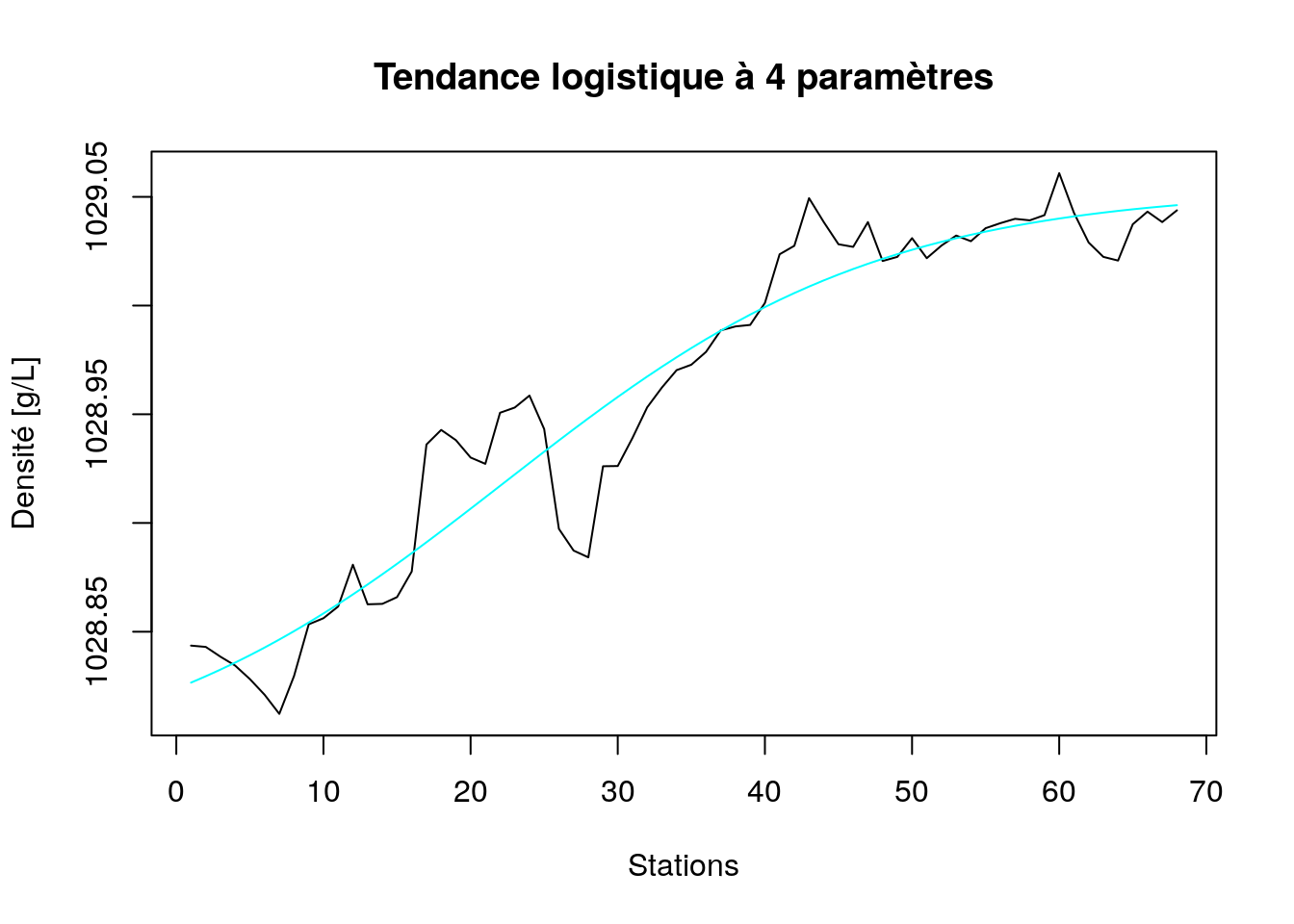
Ce dernier modèle est particulièrement intéressant parce qu’il exprime un changement de densité progressif entre la densité côtière vers Nice plus basse et celle plus élevée rencontrée en Corse. Les paramètres A et B sont les estimations de ces deux densités. Nous avons donc ici choisi un modèle qui exprime aussi un phénomène physique bien réel au travers de l’équation du modèle. C’est évidemment un gros plus. D’autant plus que ce modèle s’ajuste très bien dans les données !
Nous pouvons à présent extraire la composante résiduelle pour observer les anomalies de densité par rapport à cette tendance générale :
density_ano <- extract(density_logisdec, components = "residuals")
plot(density_ano, xlab = "Stations", ylab = "Anomalies de densité [g/L]")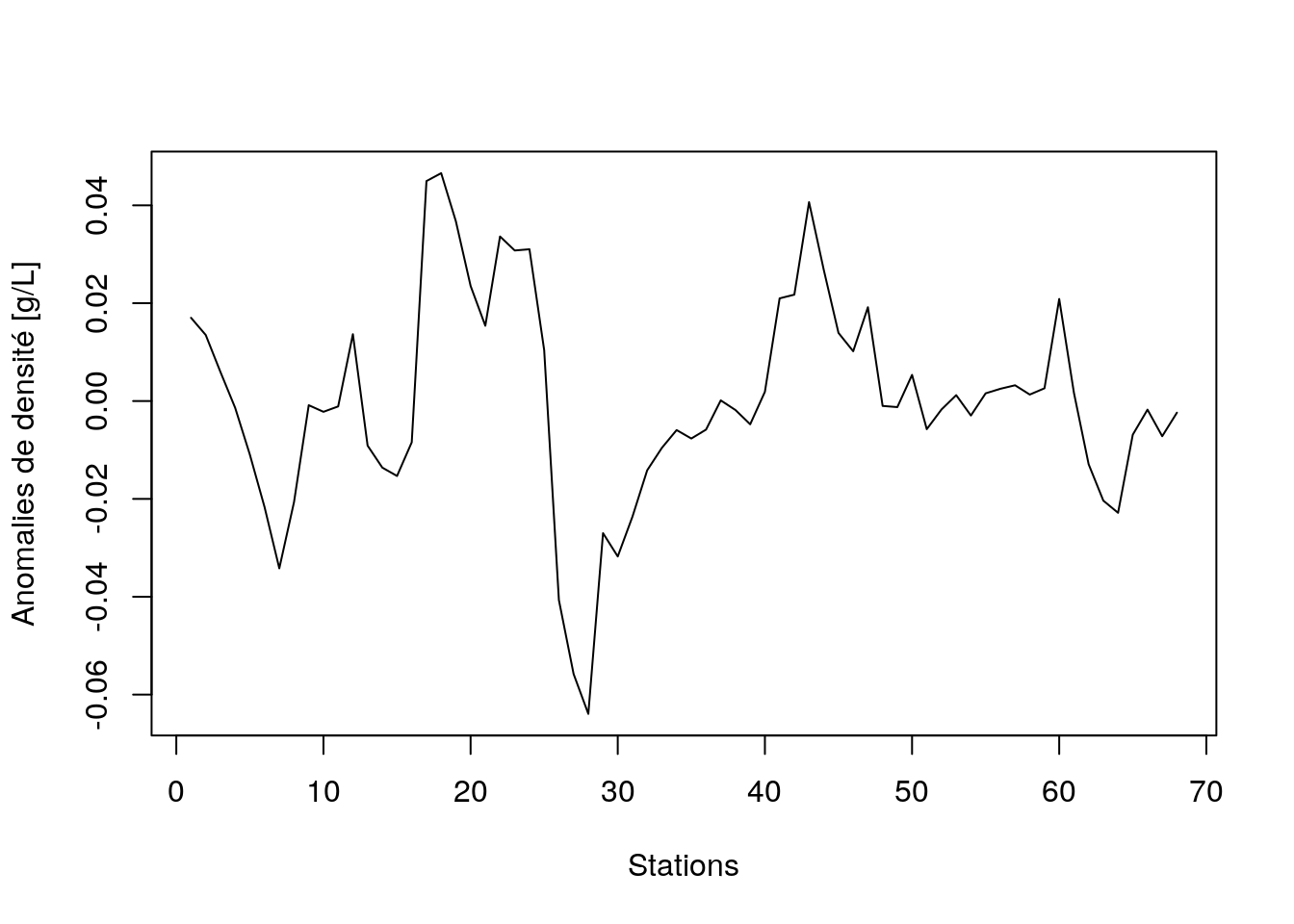
A partir de là, nous pouvons analyser classiquement cette nouvelle série. Notez la diminution importante de densité au niveau du front vers la station 28 qui est clairement mise en évidence maintenant.
5.3.1.2 Tendance cyclique
La tendance générale est parfois liée à l’évidence à un cycle (annuel, lunaire, etc.). La régression sinusoïdale permet de tester statistiquement, et de définir un modèle de variation rigoureusement périodique. Naturellement, ce modèle doit être utilisé avec discernement. Ainsi, même si la variabilité saisonnière existe pour des abondances d’espèces, elle ne s’ajuste pas forcément à une sinusoïde si les amplitudes maximums sont décalées d’une année à l’autre, d’un mois ou plus. Et si alors on étudie les écarts entre les valeurs observés et le modèle, ceux-ci ne correspondent plus à une variabilité indépendante de la variation saisonnière. Ils ne représentent que l’inadéquation du modèle choisi, qui lui, est strictement périodique.
Grâce à une astuce, nous pouvons ajuster un modèle sinusoïdal à l’aide de la fonction lm() dans R. Il suffit de rendre l’équation linéaire par un changement de variables. Rappelez-vous que nous avons vus dans le précédent module qu’une sinusoïde correspond à l’équation suivante :
\[X_t = A \cdot \cos(2 \pi \omega t + \phi)\]
avec \(\omega\) la fréquence du signal, \(\phi\) son déphasage et \(A\) son amplitude. Mais nous avons aussi vu qu’il est possible de reparamétrer cette forme en une somme de sinus et cosinus :
\[A \cdot \cos(2 \pi \omega t + \phi) = \beta_1 \cdot \cos(2 \pi \omega t) + \beta_2 \cdot \sin(2 \pi \omega t)\]
Dès lors, et à condition de cibler une fréquence particulière \(\omega\) connue à l’avance pour le cycle (par exemple, pour un cycle saisonnier on sait d’avance que la fréquence est d’exactement un an), nous pouvons calculer deux variables issues de \(t\) : \(T_1 = \cos(2 \pi \omega t)\) et \(T_2 = \sin(2 \pi \omega t)\). Ainsi, nous obtenons l’équation suivante :
\[\beta_1 \cdot T_1 + \beta_2 \cdot T_2\]
Cette dernière forme est assimilable à une régression multiple sur deux variables indépendantes \(T_1\) et \(T_2\) dont l’ordonnée à l’origine vaut zéro, et que nous pouvons ajuster facilement à l’aide de la fonction lm().
Exemple
Nous avons déjà ajusté un tel modèle dans le jeu de données co2 plus haut, mais sans l’expliquer complètement. A présent que nous avons vu l’astuce de la substitution de variable dans la forme sinus/cosinus de l’équation de la courbe sinusoïdale, nous comprenons mieux comment nous avons procédé. Utilisons maintenant un modèle sinusoïdal pour estimer la variation de la température au château de Nottingham pendant 20 ans au 20èmesiècle. Comme les températures sont enregistrées en °F, nous nous empressons de les convertir en °C (°C = (°F - 32) / 1.8).
data("nottem", package = "datasets")
nottem <- (nottem - 32) / 1.8 # °F -> °C
tsp(nottem) # Données mensuelles, unité: 1 an# [1] 1920.000 1939.917 12.000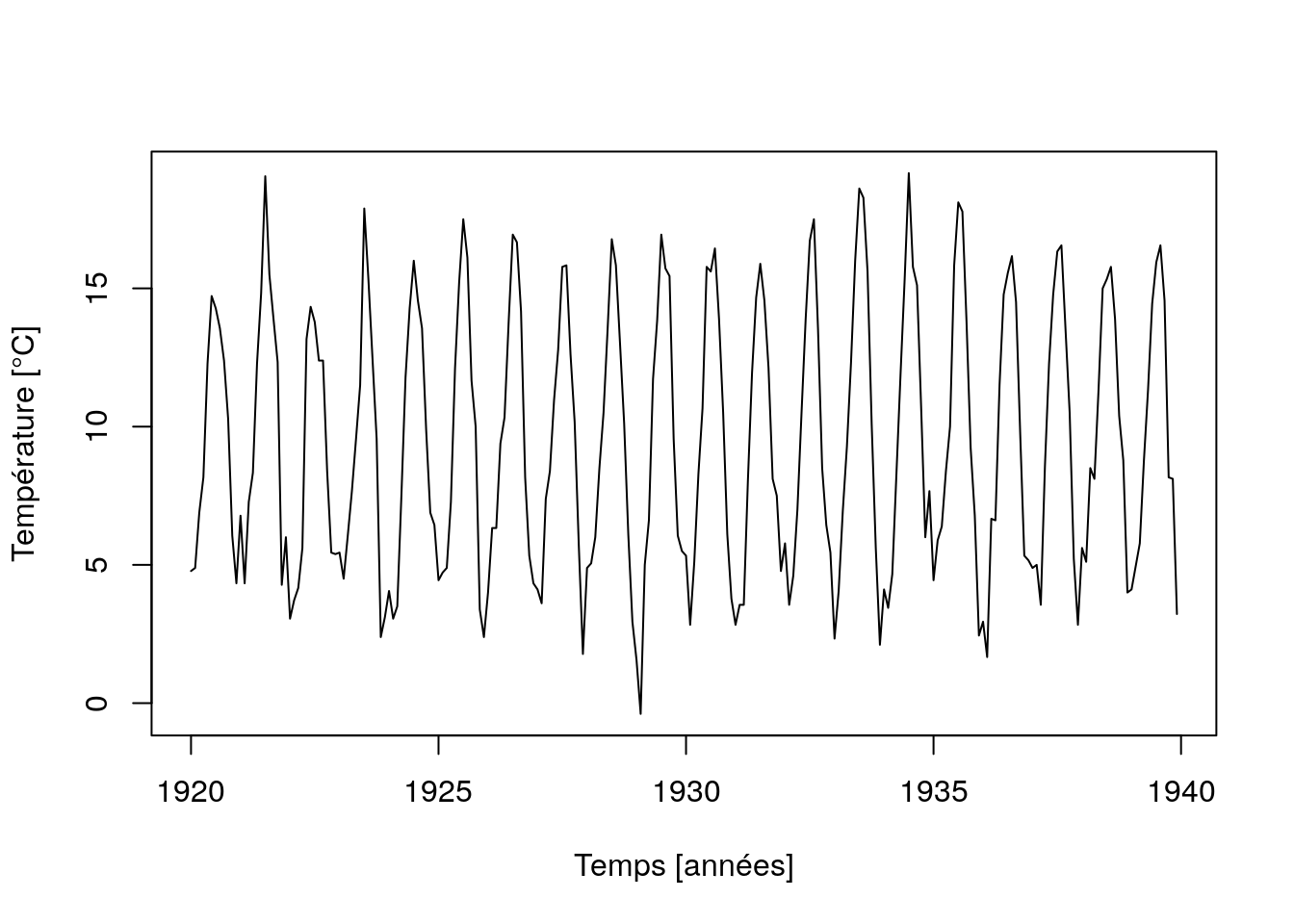
Comme l’unité de temps choisie ici est l’année, et que cela correspond à la la fréquence du signal voulu, nous avons donc \(\omega = 1\).
t <- time(nottem)
omega <- 1 # Fréquence fixée à 1 an pour le signal sinusoïdal
nottem_sin <- lm(nottem ~ I(cos(2*pi*omega*t)) + I(sin(2*pi*omega*t)))
coef(nottem_sin)# (Intercept) I(cos(2 * pi * omega * t))
# 9.4664352 -6.3740696
# I(sin(2 * pi * omega * t))
# -0.7725222nottem_sindec <- tsd( nottem, method = "reg", xreg = predict(nottem_sin))
plot(nottem_sindec, stack = FALSE, resid = FALSE, col = 1:2,
xlab = "Temps [années]", ylab = "Température [°C]",
main = "Variations saisonnière sinusoïdales")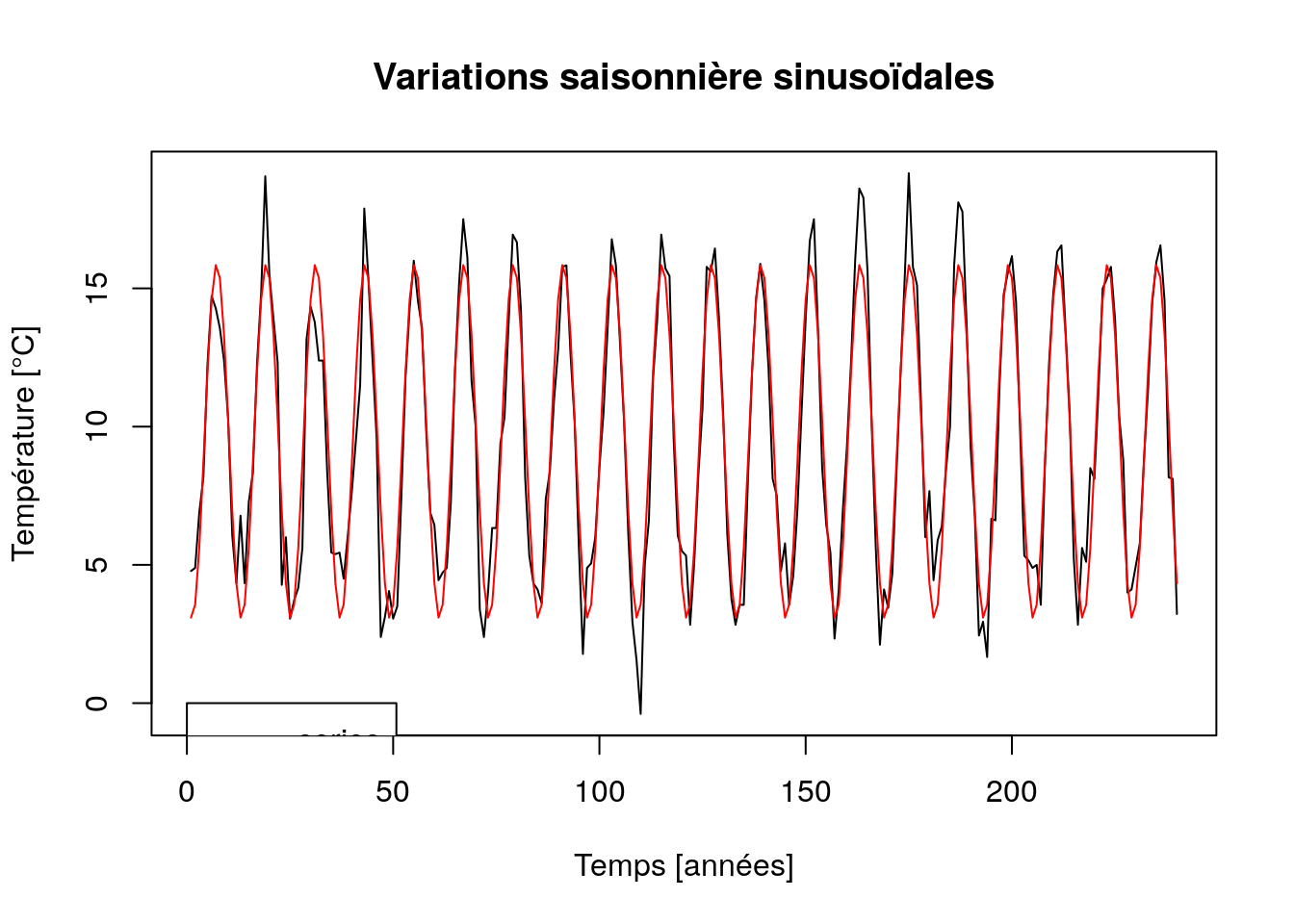
Notre modèle sinusoïdal semble s’adapter relativement bien pour représenter les températures. Nous voyons immédiatement où se situent les années à étés plus chauds, et les hivers plus ou moins rigoureux. Nous pouvons naturellement extraire les composantes et les analyser plus avant (nous vous laissons cela comme exercice). Les résidus ici sont appelés anomalies de température par rapport au modèle choisi. Mais les météorologues préfèrent généralement utiliser dans ce cas les moyennes mensuelles des températures sur une longue période, par exemple 10 ans, ou même un siècle.