2.5 Partitionnement récursif
Le partitionnement récursif est un algorithme de classification supervisée qui créé un arbre dichotomique où, à chaque nœud, une variable permet de déterminer si le parcours de l’arbre doit être poursuivi vers la gauche du nœud (lorsque la valeur de la variable est inférieure à un seuil fixé), ou vers sa droite (si la valeur est supérieure ou égale à ce seuil). Le choix de la variable utilisée à chaque nœud, ainsi que la valeur du seuil, sont déterminés par l’algorithme de façon à maximiser la séparation entre les deux sous-entités ainsi obtenus, qui doivent discriminer au mieux entre les différentes groupes à identifier. Le traitement est poursuivi tout au long de l’arbre de manière récursive jusqu’à aboutir à une extrémité, nommée “feuille”, et qui représente une classe donnée. Notez qu’il peut très bien y avoir plusieurs feuilles qui représentent une même classe. La classe attribuée à un individu est donc celle à laquelle on abouti après avoir parcouru l’arbre de la base jusqu’aux feuilles.
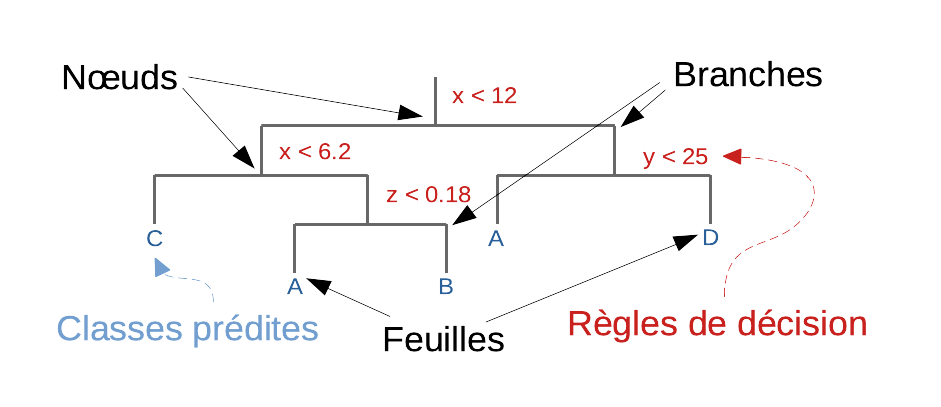
Schéma du principe d’un arbre de classification en 4 classes, A, B, C et D en utilisant les attributs x, y et z. A chaque nœud un attribut et un seuil sont choisis afin d’établir une règle de décision (en rouge). Pour un individu dont il faut prédire la classe, nous parcourons l’arbre de branche en branche depuis tout en haut et bifurquons à gauche ou à droite selon la comparaison à la règle à chaque nœud : vers la gauche si la variable est inférieure au seuil, vers la droite si elle est supérieure ou égale. Les feuilles représentent chacune une classe (en bleu, duplications possibles). Arrivé à une feuille, nous obtenons donc la classe prédite pour cet individu.
Vous pouvez aussi visionner une magnifique présentation animée de ce qu’est un arbre de partitionnement ou décisionnel (pensez bien à sélectionner le français en tout début de document et faites défiler jusqu’à la fin de l’histoire). Dans cette présentation, la notion de suréchantillonnage (oversampling en anglais) est abordé. C’est un problème qui se rencontre souvent en classification supervisée, tout comme en régression. Dans le cas de l’arbre de partitionnement, la solution consiste à élaguer les branches de moindre importance de l’arbre. Cette page explique de manière très claire de quoi il s’agit.
2.5.1 Pima avec rpart
Afin de rendre ceci plus concret, calculons l’arbre de partitionnement récursif pour pima1. Le package {mlearning} ne proposant pas cette fonction, nous utiliserons rpart() du package du même nom avec les différents arguments par défaut. Les méthodes plot() et text() permettent de tracer l’arbre décisionnel calculé. Nous aurons aussi besoin plus tard du package {ipred} pour réaliser la validation croisée.
library(rpart)
library(ipred)
pima1_rpart <- rpart(data = pima1, diabetes ~ .)
# Visualisation et annotation de l'arbre
# Les différents arguments qui contrôlent l'apparence
# du graphiques sont expliqués dans ?plot.rpart
plot(pima1_rpart, margin = 0.03, uniform = TRUE)
text(pima1_rpart, use.n = FALSE)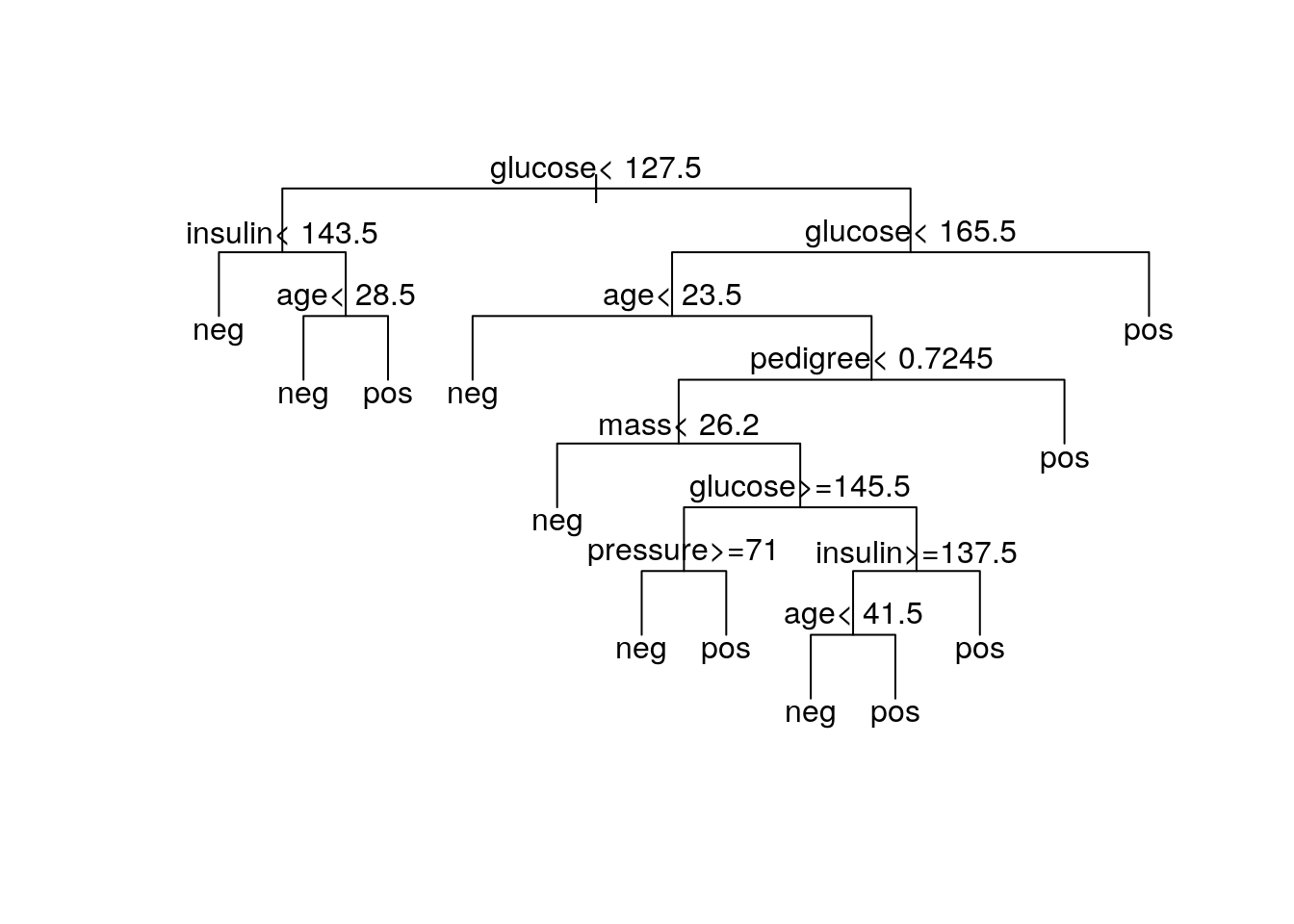
Comment lire cet arbre ? Nous partons de tout en haut, et à chaque nœud correspond une variable et un seuil. Si la variable est inférieur au seuil, nous parcourons l’arbre vers la gauche. Si au contraire, la variable est supérieure ou égale au seuil, nous nous dirigeons vers la droite. Nous réitérons l’opération à chaque nœud, jusqu’à arriver à une feuille. A ce niveau, nous lisons la classe associée à la feuille que nous attribuons à l’individu. Considérons un femme Pima pour laquelle nous avons enregistré les informations suivantes :
- âge = 34 ans,
- elle a 4 enfants (
pregnant), - son test glucose a donné la valeur de 118 et son insuline a été mesurée à 145 µU/mL,
- sa pression sanguine est de 82 mm Hg (
pressure), - au niveau corpulence, elle a un IMC de 33,2 (
mass) et le pli de peau au niveau de son triceps est de 28 mm, - enfin son indice de susceptibilité au diabète d’après ses antécédents familiaux a été calculé à 0,43.
D’après notre classifieur par arbre de partitionnement, est-elle diabétique ou non ? Pour y répondre, nous devons traverser l’arbre de haut en bas jusqu’à aboutir à une feuille.
La première règle rencontrée est “glucose < 127,5”. Comme la valeur mesurée est de 118, nous continuons vers la gauche,
Seconde règle rencontrée : “insulin < 143,5”. La valeur mesurée est de 145. Cette fois, nous bifurquons à droite,
Nous arrivons à la règle “age < 28,5”. A 33 ans, nous continuons à nouveau vers la droite pour aboutir à une feuille de l’arbre
pos. Ainsi pour cette dame, la prédiction est qu’elle est diabétique.
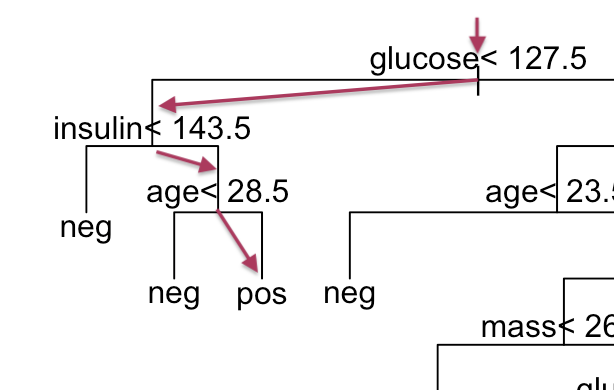
Chemin parcouru dans notre arbre décisionnel pour aboutir à la décision que l’indienne de notre exemple est probablement diabétique.
Notons que toutes les variables n’ont pas été utilisées. glucose et age sont repris trois fois dans l’arbre. Les variables insulin, mass, pressure et pedigree sont également utilisées. Par contre, triceps n’est jamais utilisée, de même que pregnant. C’est une première indication de l’importance des variables dans la discrimination des classes, même si la version à partir de la forêt aléatoire à base de l’indice Gini (voir plus loin) sera plus efficace.
Poursuivons notre étude. Si nous voulons utiliser la validation croisée, nous devons définir la fonction cvpredict_rpart() de manière similaire à ce que nous avions fait pour cvpredict_knn().
cvpredict_rpart <- function(formula, data, cv.k = 10, ...) {
# Forcer predict() à renvoyer les classes automatiquement
predict_class <- function(object, newdata)
predict(object, newdata = newdata, type = "class")
error <- errorest(formula, data = data, model = rpart,
estimator = "cv", predict = predict_class,
est.para = control.errorest(k = cv.k, predictions = TRUE), ...)
# Ce sont les prédictions que nous voulons
error$predictions
}Avec cette fonction cvpredict_rpart() nous ferons le calcul comme suit, en utilisant tous les paramètres par défaut pour rpart() :
set.seed(861)
pima1_rpart_sv <- cvpredict_rpart(data = pima1, diabetes ~ ., cv.k = 10)
pima1_rpart_conf <- confusion(pima1_rpart_sv, pima1$diabetes)
plot(pima1_rpart_conf)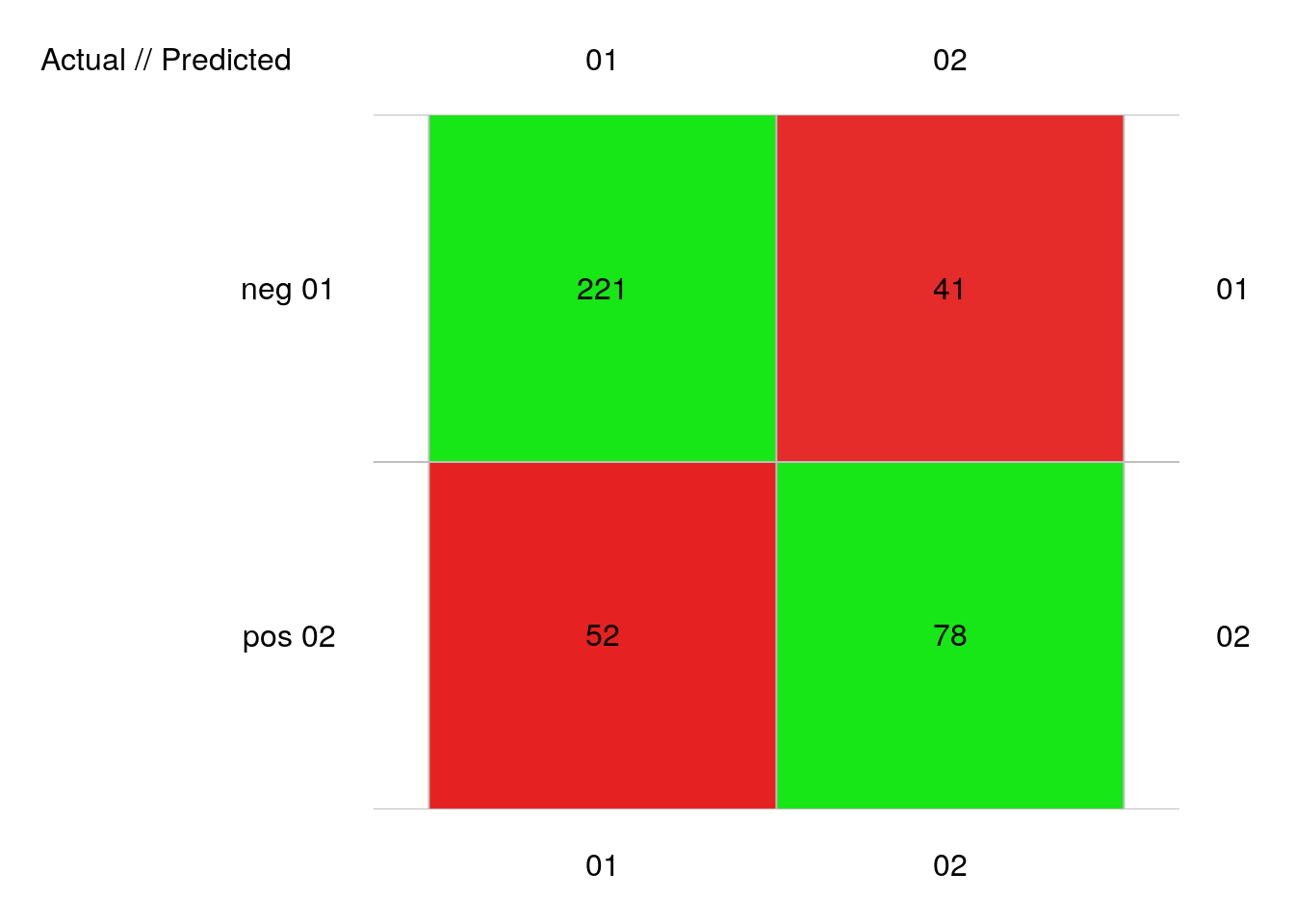
# 392 items classified with 299 true positives (error = 23.7%)
#
# Global statistics on reweighted data:
# Error rate: 23.7%, F(micro-average): 0.727, F(macro-average): 0.726
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8261682 0.8435115 0.8095238 0.6000000 0.6554622 0.4000000 0.1564885
# pos 0.6265060 0.6000000 0.6554622 0.8435115 0.8095238 0.1564885 0.4000000
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.1904762 0.3445378 2.108779 0.2608142 2.349593 0.2905983 0.7217557
# pos 0.3445378 0.1904762 3.834146 0.4742081 3.441176 0.4256055 0.7217557
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.4541218 80.84083 0.01403061 273 262 11 221 52 41 78
# pos 0.4541218 80.84083 0.01403061 119 130 -11 78 41 52 221Nous obtenons un peu moins de 24% d’erreur, ce qui se situe dans une bonne moyenne par rapport aux autres algorithmes déjà étudiés.
set.seed(8435)
pima2_rpart_cv <- cvpredict_rpart(data = pima2, diabetes ~ ., cv.k = 10)
pima2_rpart_conf <- confusion(pima2_rpart_cv, pima2$diabetes)
plot(pima2_rpart_conf)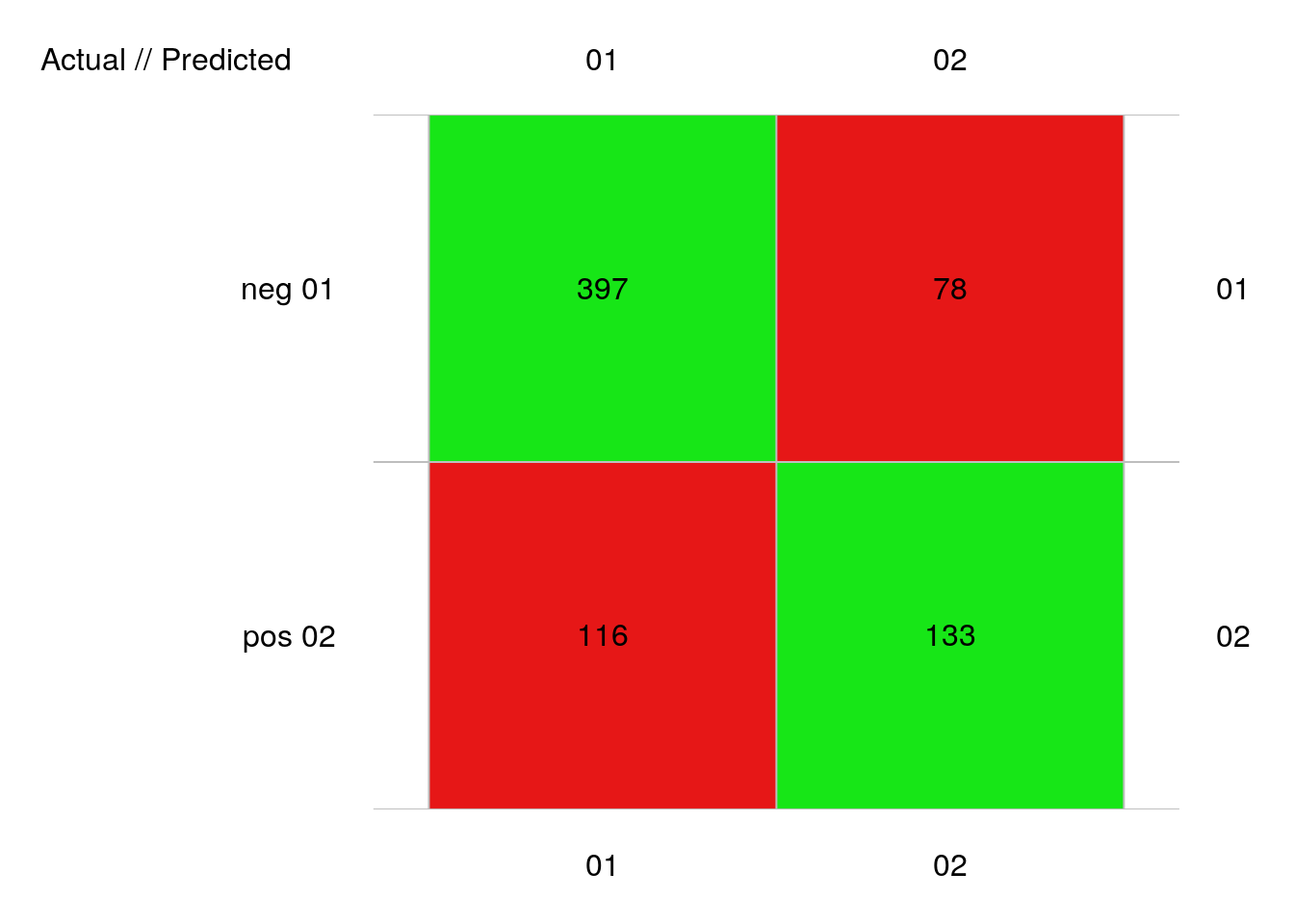
# 724 items classified with 530 true positives (error = 26.8%)
#
# Global statistics on reweighted data:
# Error rate: 26.8%, F(micro-average): 0.693, F(macro-average): 0.691
#
# Fscore Recall Precision Specificity NPV FPR FNR
# neg 0.8036437 0.8357895 0.7738791 0.5341365 0.6303318 0.4658635 0.1642105
# pos 0.5782609 0.5341365 0.6303318 0.8357895 0.7738791 0.1642105 0.4658635
# FDR FOR LRPT LRNT LRPS LRNS BalAcc
# neg 0.2261209 0.3696682 1.794065 0.3074317 2.093442 0.3587331 0.684963
# pos 0.3696682 0.2261209 3.252755 0.5573933 2.787588 0.4776821 0.684963
# MCC Chisq Bray Auto Manu A_M TP FP FN TN
# neg 0.3866887 108.2584 0.02624309 513 475 38 397 116 78 133
# pos 0.3866887 108.2584 0.02624309 211 249 -38 133 78 116 397Ah ? Ici, nous nous approchons de 27%, notre variable insulin de pima1 semble être plus utile à cette méthode qu’un nombre plus grand d’individus dans pima2.
Pour en savoir plus
- Explication sur la façon dans les règles sont établies dans l’arbre ici.