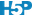4.1 Observations dépendantes du temps
Démarrons tout de suite notre étude des séries chronologiques par plusieurs exemples concrets qui vont nous emmener dans les plaines enneigées du grand Nord Canadien, au sommet d’un volcan à Hawaï, dans le cerveau d’un patient épileptique ou au large de la Mer Méditerranée.
4.1.1 Lynx
Vous vous intéressez au Lynx du Canada (Lynx canadensis) du point de vue de la dynamique de population à long terme de l’espèce. Afin de réaliser une étude rétrospective, vous recherchez la meilleure façon de déterminer la variation inter-annuelle de cette espèce à l’époque où elle était encore abondante (au 19ème siècle et au début du 20ème siècle).

Lynx du Canada par Eric Kilby
Il apparaît que le nombre de lynx capturés par les trappeurs de l’époque est la meilleure information que vous puissiez obtenir (observations indirectes, ou “proxy” dans le jargon statisticien). La compilation de données de captures entre 1821 et 1934 en nombre d’individus donne ceci1 :
Nous sommes tout de suite surpris par la variation importante dans les captures d’une année à l’autre. Il semble que les années de captures abondantes reviennent à intervalle régulier. Mais comment analyser plus à fond ces données ? Notons d’emblée que l’unité d’échantillonnage (territoire Canadien) est la même pour chaque mesure. Donc, il n’y a pas indépendance des observations les unes par rapport aux autres. Intuitivement nous pouvons d’ailleurs facilement imaginer cela. Connaissant les captures à une année, nous pouvons considérer que celles l’année d’avant ou l’année d’après ne sont pas complètement indépendantes, puisqu’il s’agit de la même population de lynx qui est échantillonnée. D’ailleurs, le graphique proposé par défaut par la fonction plot(), et qui présente le temps sur l’axe X et la variable mesurée sur l’axe Y relie les points les uns aux autres en une ligne unique qui varie dans le temps. C’est la représentation standard d’une série chronologique. Le fait de relier les points indique à la fois qu’il y a variation continue et aussi qu’il y a probablement un certain degré de dépendance entre les observations.
4.1.2 CO2 à Hawaï
Nous sommes en période de grands changements climatiques et de réchauffement planétaire, ce n’est plus un secret pour personne. Une des causes identifiées de ces changements est l’augmentation du CO2 dans l’atmosphère suite à la combustion massive de combustible fossile (charbon, gaz et pétrole). Ces changements ont des effets bien visibles sur le vivant. En biologie, nous devons souvent confronter nos observations par rapport aux changements du milieux, et donc, nous manipulons fréquemment des séries chronologiques de données physico-chimiques. Le CO2 (en ppm ou parties par million) a été mesuré dans l’atmosphère au laboratoire NOAA situé en haut du volcan Mauna Loa à Hawaï.

L’observatoire situé en plein milieu de l’Océan Pacifique et à 3400m d’altitude sur le Mauna Loa à Hawaï d’où provient la série co2.
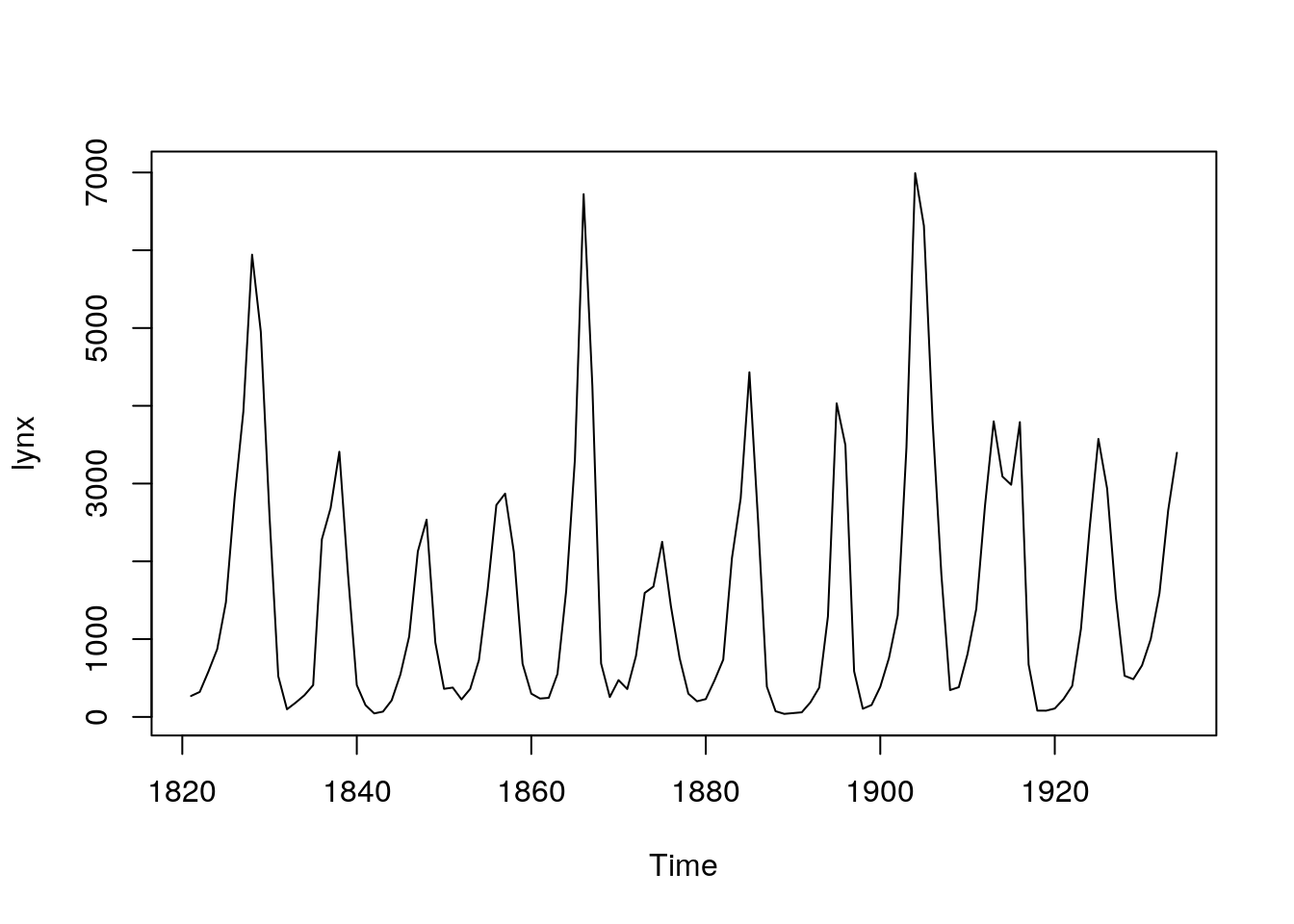
Cet observatoire est situé dans une zone suffisamment éloignée des principales sources industrielles de production de CO2, en plein milieu de l’Océan Pacifique, pour que les mesures n’en soient pas affectées. Les données suivantes présente l’évolution du CO2 atmosphérique entre 1959 et 1998 :
Ici aussi, nous observons très clairement des variations qui se répètent à intervalle régulier, probablement des variations saisonnières. Mais par dessus ces fluctuations, une augmentation à plus long terme est effectivement particulièrement visible. Une fois de plus, les différentes observations ont toutes été réalisées au même endroit et une forte interdépendance est à suspecter.
4.1.3 EEG
L’électro-encéphalogramme consiste à mesurer des manière non invasive l’activité électrique de notre cerveau. L’épilepsie est un dérèglement majeur du fonctionnement cérébral qui se marque particulièrement bien au niveau de l’EEG.
EEG en cours de mesure par Baburov.
Le graphique suivant montre à quoi ressemble un signal enregistré par un EEG pendant une crise d’épilepsie (sachant qu’il y a autant de signaux différents que d’électrodes utilisées) :
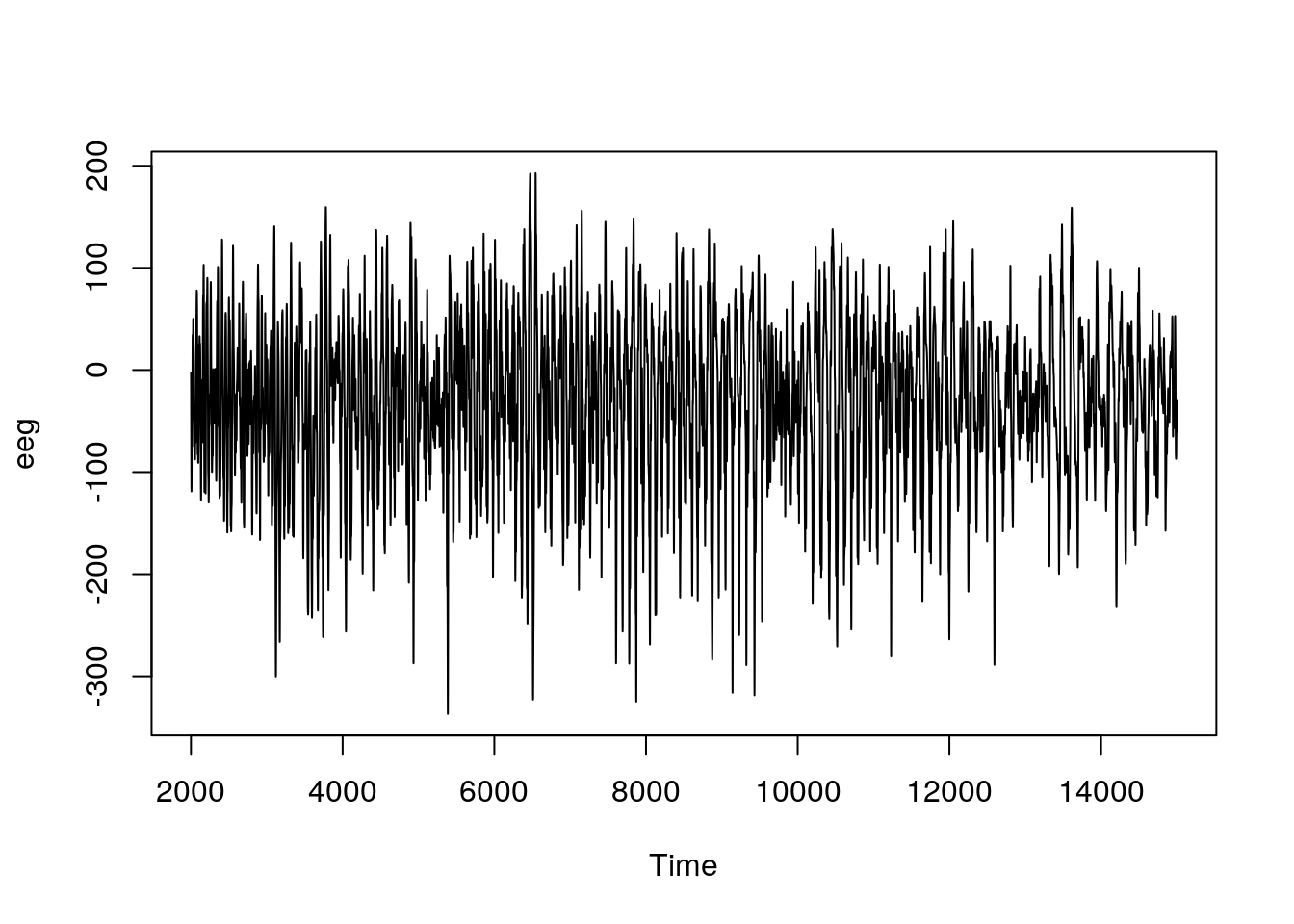
Ici, la série chronologique est comptabilisée sur l’axe du temps simplement avec le numéro de la mesure commençant par 2001, mais en réalité, 256 mesures sont réalisées par seconde ici. Dans cette série, les fluctuations sont importantes, mais apparaissent difficiles à interpréter sur le graphique brut.
4.1.4 Plancton méditerranéen
Les séries chronologiques sont aussi appelées séries spatio-temporelles car sous certaines conditions, elles peuvent aussi servir à représenter des évènements qui varient spatialement, voir dans l’espace et le temps simultanément. Mais attention, quand nous parlons de variation spatiale, il ne peut s’agir que de variation unidimensionnelle, par exemple, le long d’un transect (tracé rectiligne ou non entre deux points et le long duquel les mesures sont réalisées). Un bon exemple d’une telle variation spatio-temporelle est représentée par l’étude du plancton en Mer Méditerranée entre Nice et la Corse.
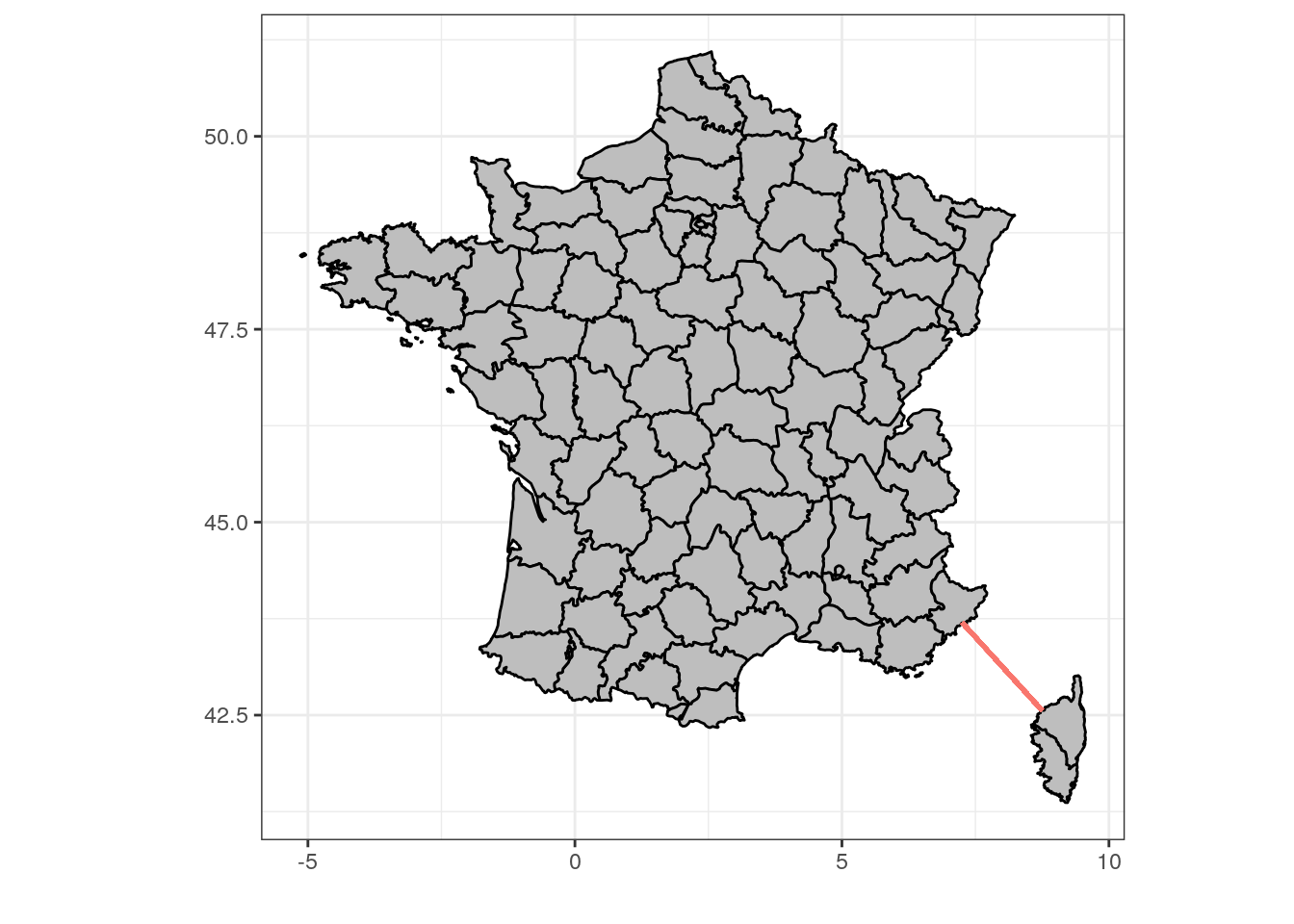
Figure 4.1: Une séries de 68 stations équiréparties le long d’un transect entre Nice et la Corse (trait rouge) sont échantillonnées pour la physico-chimie (marphy) et le plancton (marbio).
Nous avons ici effectivement un axe qui varie spatialement le long du transect, mais en même temps dans le temps car les 68 stations ne sont pas échantillonnées simultanément, mais successivement dans le temps au fur et à mesure que le navire océanographique fait route entre Nice et Calvi en Corse. Nous avons déjà utilisé ces données au cours SDD II pour illustrer les analyses multivariées. Voyons ce que donnent les paramètres physico-chimiques sous forme de séries spatio-temporelles (notez que, comme marphy est un dataframe, nous utilisons la fonction ts() pour le transformer en séries spatio-temporelles, plus de détails sur cette dernière fonction seront donnés plus loin) :
marphy <- ts(read("marphy", package = "pastecs"))
plot(marphy, main = "Masses d'eaux entre Nice et la Corse",
xlab = "Transect Nice - Calvi (stations)")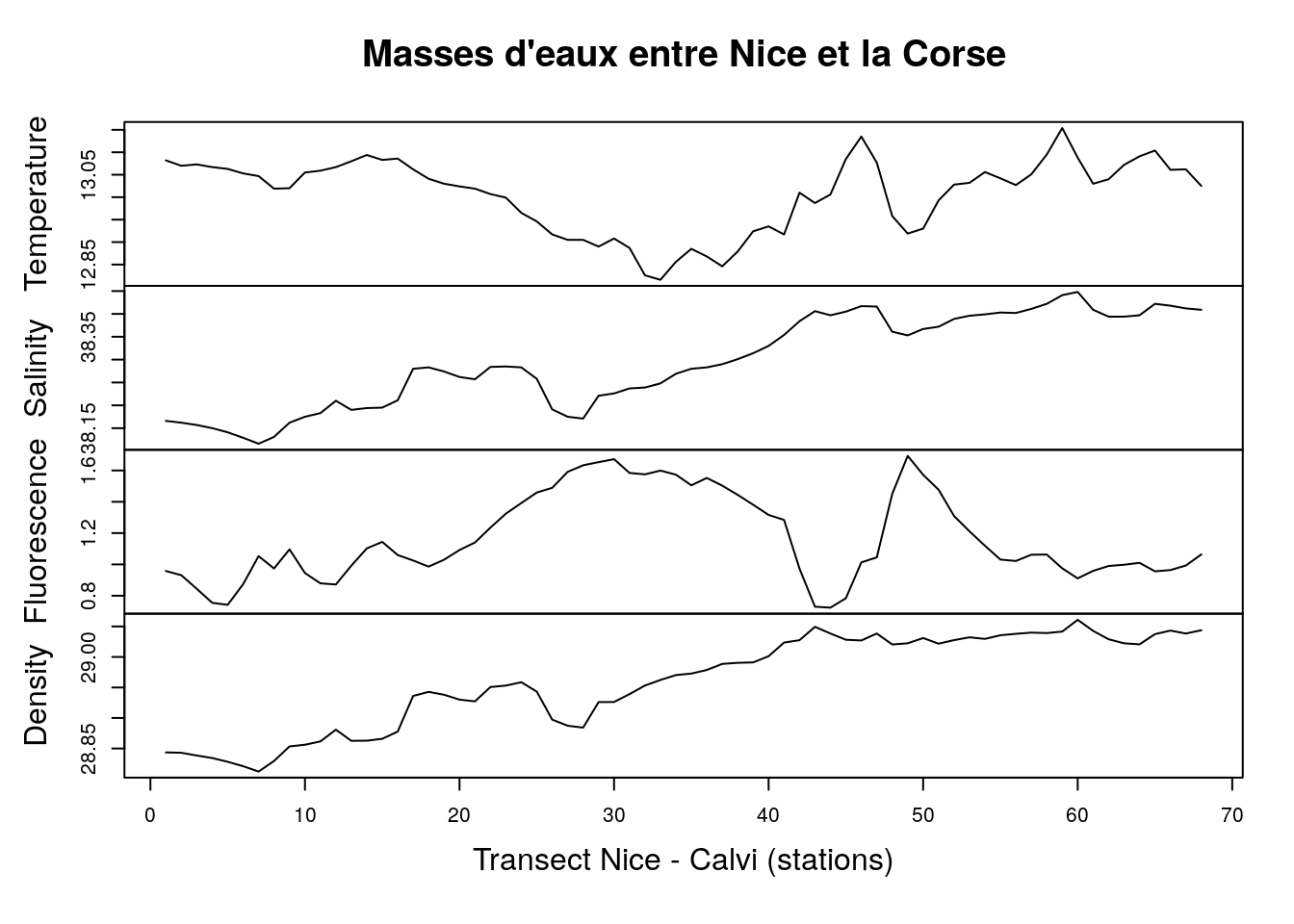
Ici, nous avons pour rappel quatre variables enregistrées : la température (°C), la salinité de l’eau, la fluorescence (de la chlorophylle) qui est une mesure indirecte du contenu en phytoplancton dont l’abondance dépend elle-même du contenu en sels nutritifs (azote, phosphore, silice), et enfin la densité de l’eau en g/L. Nous observons ici des variations importantes et parfois assez abruptes. En fait, le transect croise un front constitué par une remontée d’eaux profondes, froides et riches en nutriments en plein milieu. De même, marbio est un dataframe que nous nous empressons de convertir avec ts(), mais ici nous choisissons trois séries parmi l’ensemble des 24 séries pour la représentation graphique à l’aide de l’opérateur [,] :
marbio <- ts(read("marbio", package = "pastecs"))
colnames(marbio) # Nom des différentes séries dans le jeu de données multivarié# [1] "Acartia" "AdultsOfCalanus" "Copepodits1"
# [4] "Copepodits2" "Copepodits3" "Copepodits4"
# [7] "Copepodits5" "ClausocalanusA" "ClausocalanusB"
# [10] "ClausocalanusC" "AdultsOfCentropages" "JuvenilesOfCentropages"
# [13] "Nauplii" "Oithona" "Acanthaires"
# [16] "Cladocerans" "EchinodermsLarvae" "DecapodsLarvae"
# [19] "GasteropodsLarvae" "EggsOfCrustaceans" "Ostracods"
# [22] "Pteropods" "Siphonophores" "BellsOfCalycophores"plot(marbio[, c("Acartia", "ClausocalanusA", "Pteropods")],
main = "Plancton entre Nice et la Corse",
xlab = "Transect Nice - Calvi (stations)")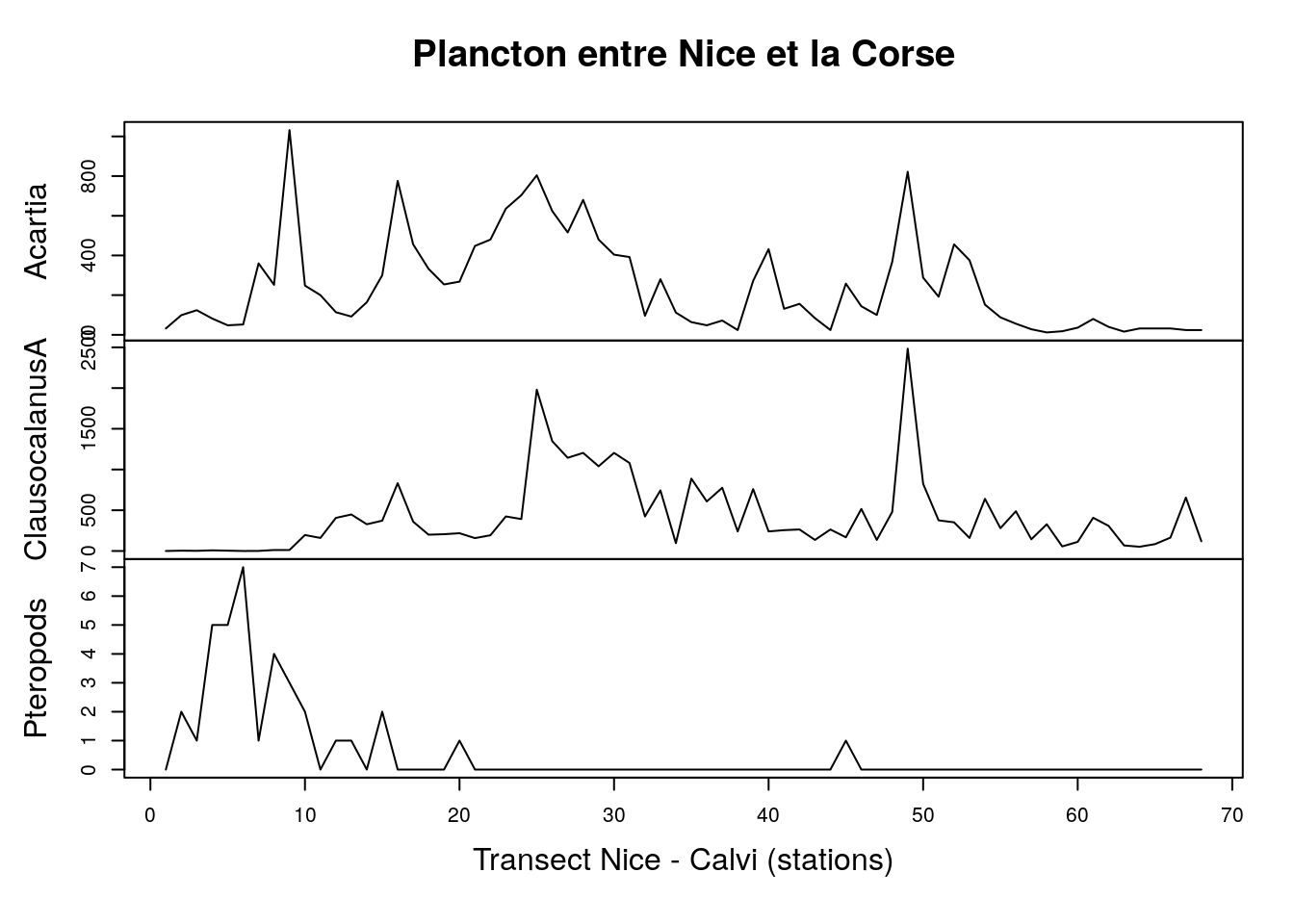
Ici aussi la distribution du plancton le long du transect n’est pas homogène. Alors que les ptéropodes (mollusques planctoniques) se retrouvent essentiellement près de Nice, les crustacés copépodes comme Acartia spp ou Clausocalanus spp se retrouvent plutôt en pleine mer.
Notez que nous n’utilisons pas
read()ici pour lire ces données, maisdata(); En effet,read()convertit les données en data frame, mais nous voulons les conserver dans leur format d’origine sans conversion. De même, nous utilisonsplot()et non paschart()pour réaliser le graphique de base le plus approprié pour cet objet.↩︎