2.3 K plus proches voisins

K plus proches voisins (k-nearest neighbours en anglais ou k-NN en abbrégé) est certainement la technique la plus intuitive en classification supervisée. Malgré sa simplicité inhérente, elle offre de bonnes prestations. La classification supervisée s’effectue par une analyse de la matrice de distances de Mahalanobis (équivalente à la distance Euclidienne ou géométrique appliquée sur des données réduites de variance unitaire) entre un individu d’intérêt à reconnaître et les individus du set d’apprentissage.

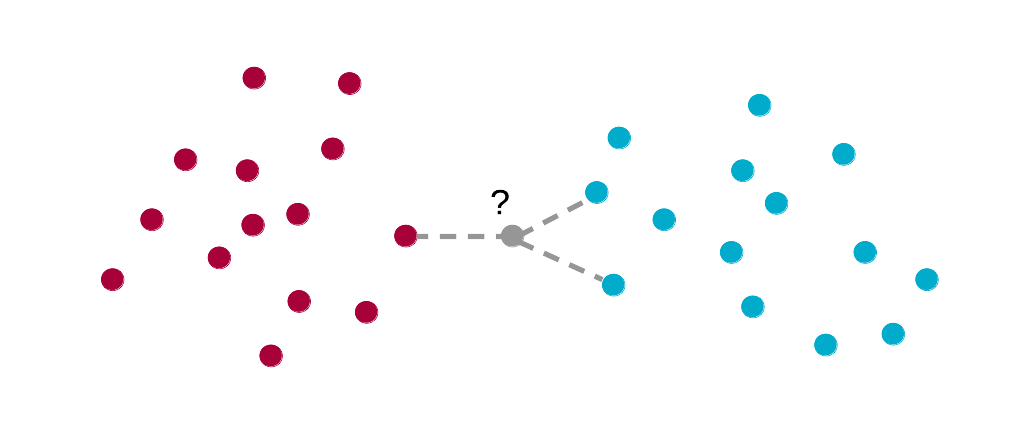
La classification par les k plus proches voisins compare un individu inconnu (en gris) avec les individus de classe connue du set d’apprentissage (bleus et rouges matérialisant deux classes différentes) du point de vue de la distance de Mahalanobis. Ici k = 3, et l’individu inconnu est considéré comme bleu puisqu’il est plus proche de deux bleus contre un seul rouge.

En d’autres termes, il s’agit tout simplement de calculer la distance géométrique qui sépare un individu d’intérêt de tous les individus du set d’apprentissage dans un espace réduit, c’est-à-dire, un espace où chaque variable est mise à l’échelle de telle manière que sa variance soit unitaire. La classe attribuée à l’individu d’intérêt sera la même que celle du, ou des k individus les plus proches (d’où le nom de la méthode). Des variantes utilisent naturellement d’autres calculs de distances : euclidiennes, manhattan, etc.

Un seul paramètre doit donc être définit : k, représentant le nombre d’individus proches considérés. Un vote à la majorité permet de déterminer à quel groupe appartient l’objet testé. En cas d’ex-æquos, la classe de l’individu du set d’apprentissage le plus proche est utilisée. Pour minimiser le risque d’ex-æquos, k est généralement choisi impair. Dans notre schéma, nous utilisons k = 3, valeur qui s’est avérée optimale dans beaucoup de situations. La recherche de la valeur optimale de k dans le cadre de l’application finale sera évidemment possible ultérieurement.

2.3.1 Pima avec k-NN

Le package {mlearning} ne propose pas encore cette méthode, mais nous pouvons utiliser des fonctions des packages {MASS} ou {ipred}.

library(ipred)
# Modèle sur toutes les données avec k = 3
pima1_knn <- ipredknn(data = pima1, diabetes ~ ., k = 3)
# La prédiction des classes se fait en précisant type = "class"
pima1_knn_pred <- predict(pima1_knn, pima1, type = "class")
# Ces prédictions ne sont PAS utilisables pour le test

Cela se complique avec la validation croisée, car la fonction correspondante de {ipred}, errorest() a une syntaxe très différent de ce qu’on trouve dans {mlearning}. nous définissons cvpredict_knn() qui se rapproche le plus possible de cvpredict() de {mlearning} (il n’est pas important d’en comprendre les détails).

# Redéfinir nos fonctions pour se rapprocher d'une syntaxe à la mlearning
# sur base de la fonction errorest() de {ipred}
cvpredict_knn <- function(formula, data, k.nn = 3, cv.k = 10, ...) {
  # Redéfinir knn pour utiliser k.nn
  knn <- function(formula, data, k.nn = 3, ...)
    ipredknn(formula, data = data, k = k.nn, ...)
  # Forcer predict() à renvoyer les classes automatiquement
  predict_class <- function(object, newdata)
    predict(object, newdata = newdata, type = "class")
  error <- errorest(formula, data = data, model = knn, k.nn = k.nn, 
    estimator = "cv", predict = predict_class,
    est.para = control.errorest(k = cv.k, predictions = TRUE), ...)
  # Ce sont les prédictions que nous voulons
  error$predictions
}

Avec cette fonction cvpredict_knn() nous ferons le calcul comme suit :

set.seed(3675)
pima1_knn_sv <- cvpredict_knn(data = pima1, diabetes ~ ., k.nn = 3, cv.k = 10)
pima1_knn_conf <- confusion(pima1_knn_sv, pima1$diabetes)
plot(pima1_knn_conf)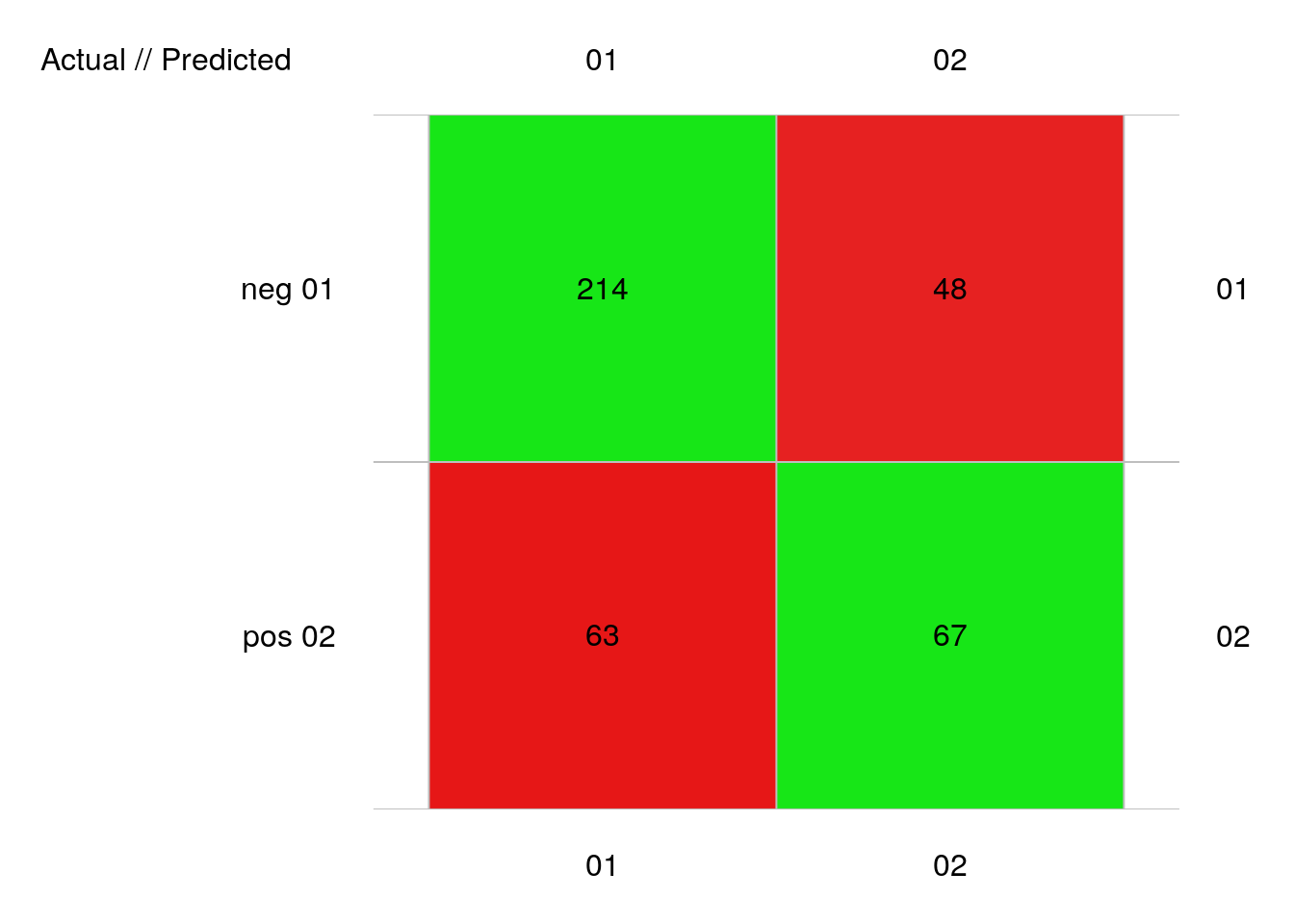

summary(pima1_knn_conf)

# 392 items classified with 281 true positives (error = 28.3%)
# 
# Global statistics on reweighted data:
# Error rate: 28.3%, F(micro-average): 0.672, F(macro-average): 0.671
# 
#        Fscore    Recall Precision Specificity       NPV       FPR       FNR
# neg 0.7940631 0.8167939 0.7725632   0.5153846 0.5826087 0.4846154 0.1832061
# pos 0.5469388 0.5153846 0.5826087   0.8167939 0.7725632 0.1832061 0.4846154
#           FDR       FOR     LRPT      LRNT     LRPS      LRNS    BalAcc
# neg 0.2274368 0.4173913 1.685448 0.3554745 1.850933 0.3903766 0.6660893
# pos 0.4173913 0.2274368 2.813141 0.5933142 2.561629 0.5402682 0.6660893
#           MCC    Chisq       Bray Auto Manu A_M  TP FP FN  TN
# neg 0.3434828 46.24834 0.01913265  277  262  15 214 63 48  67
# pos 0.3434828 46.24834 0.01913265  115  130 -15  67 48 63 214

Ici, nous avons 28% d’erreur, soit plus qu’avec l’ADL. Mais la valeur k.nn = 3 n’est pas le meilleur choix ici. Expérimentez par vous-même pour découvrir combien de plus proches voisins nous devons considérer pour minimiser l’erreur.

Pour pima2, nous obtenons :

set.seed(127)
pima2_knn_sv <- cvpredict_knn(data = pima2, diabetes ~ ., k.nn = 3, cv.k = 10)
pima2_knn_conf <- confusion(pima2_knn_sv, pima2$diabetes)
plot(pima2_knn_conf)

summary(pima2_knn_conf)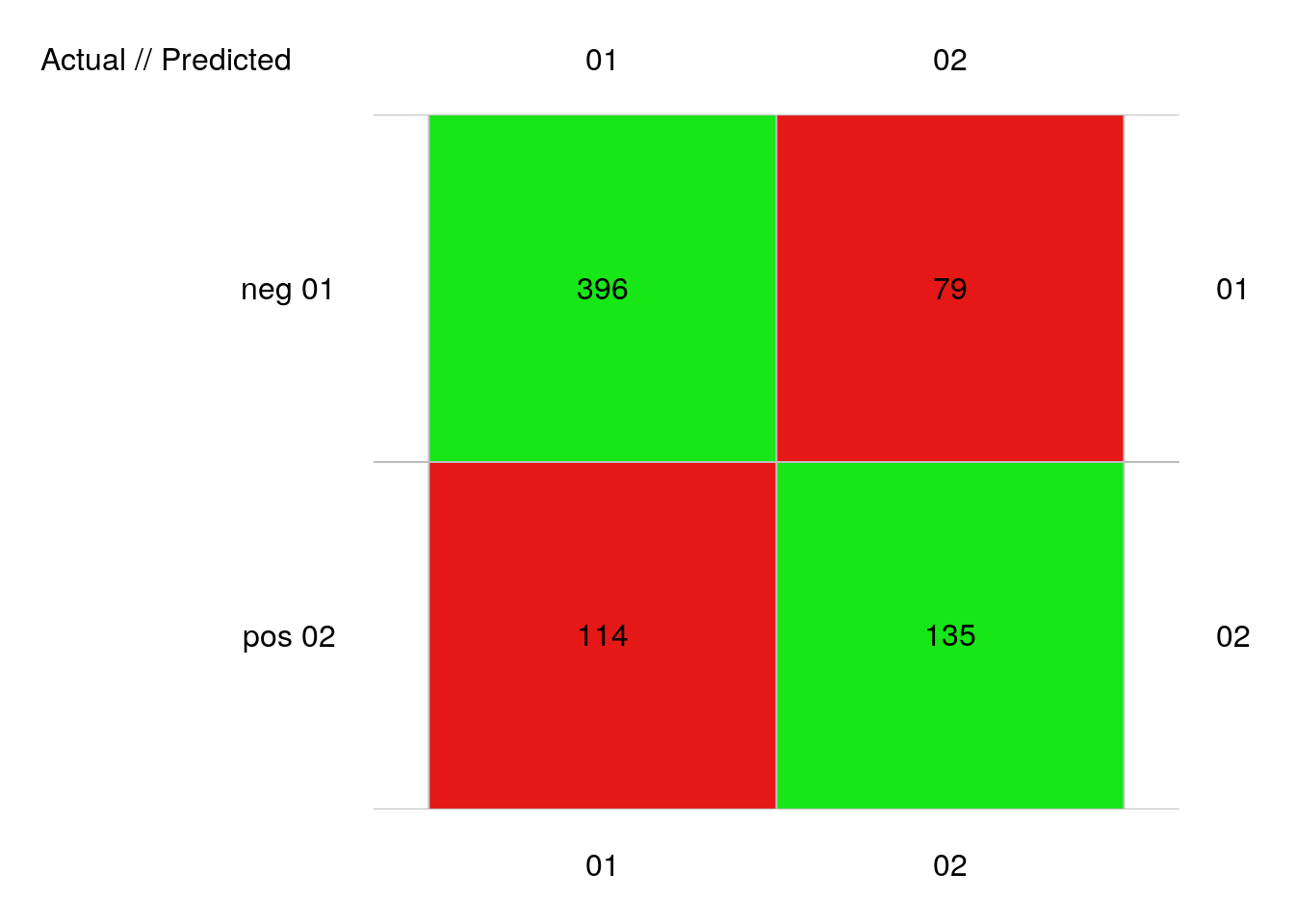

# 724 items classified with 531 true positives (error = 26.7%)
# 
# Global statistics on reweighted data:
# Error rate: 26.7%, F(micro-average): 0.696, F(macro-average): 0.694
# 
#        Fscore    Recall Precision Specificity       NPV       FPR       FNR
# neg 0.8040609 0.8336842 0.7764706   0.5421687 0.6308411 0.4578313 0.1663158
# pos 0.5831533 0.5421687 0.6308411   0.8336842 0.7764706 0.1663158 0.4578313
#           FDR       FOR     LRPT      LRNT     LRPS      LRNS    BalAcc
# neg 0.2235294 0.3691589 1.820942 0.3067602 2.103351 0.3543355 0.6879264
# pos 0.3691589 0.2235294 3.259875 0.5491664 2.822184 0.4754319 0.6879264
#           MCC    Chisq       Bray Auto Manu A_M  TP  FP  FN  TN
# neg 0.3912663 110.8366 0.02417127  510  475  35 396 114  79 135
# pos 0.3912663 110.8366 0.02417127  214  249 -35 135  79 114 396

Avec 27% d’erreur, nous avons un résultat similaire encore une fois, mais toujours légèrement moins bon que l’ADL.