1.3 Analyse discriminante linéaire
Il existe de très nombreux algorithmes de classification supervisée. Nous allons commencer la découverte des principaux algorithmes avec l’analyse discriminante linéaire. Cette analyse recherche la meilleure discrimination possible des groupes par rotation des axes, en diagonalisant la matrice variance-covariance inter-groupes, ce qui revient à calculer les combinaisons linéaires des variables initiales qui séparent le mieux ces groupes.
Il n’est pas utile ici de rentrer dans les détails mathématiques. Comme vous connaissez déjà les variances inter/intra-groupes (cf. ANOVA) d’une part, et le principe de rotation des axes de l’ACP d’autre part, vous êtes à même de comprendre le principe de l’ADL en combinant ces deux notions. Pour quantifier la séparation des différents classes ou groupes, nous allons donc réutiliser encore une fois la bonne vieille séparation de la variance totale en variance inter-groupe et variance intra-groupe que nous avons déjà employée, par exemple, dans l’ANOVA. Sauf qu’ici, nous travaillons en multivarié avec des matrices ayant potentiellement un grand nombre de dimensions. Du point de vue purement mathématique, cela ne change rien, car la partition de la variable s’applique tout aussi bien à N > 2 dimensions. Ensuite, nous nous intéressons aux distances inter-groupes. Notez que, plus ces distances sont importantes, mieux nous séparons les groupes (ou si vous préférez, les classes de notre classifieur).
Pour rappel, l’ACP est une technique qui effectue la diagonalisation d’un matrice (matrice variance-covariance, ou matrice de corrélation des données). D’un point de vue géométrique, nous avons vu que diagonaliser une matrice revient en fait à effectuer une rotation du système d’axes représenté par cette matrice, de sorte que les nouveaux axes ainsi obtenus correspondent à une maximisation de la variance sur les nouveaux axes. En ACP, on cherchait à “étaler” les données le plus possible sur les deux ou trois premiers axes afin de visualiser comment les points (les individus) se répartissent.
En ADL, on réutilise le même principe, mais nous substituons la matrice inter-groupes à la matrice variance-covariance pour effectuer cette ACP. Le résultat est une autre rotation des axes qui va maximiser, cette fois-ci, les distances inter-groupes… et donc, étaler au mieux les différentes classes de notre classifieur selon des axes qui les séparent le mieux possible linéairement (entendez par là, par une division à l’aide d’hyperplans qui sont les équivalents à N dimension de droites de séparation dans un plan à deux dimensions, voir schéma ci-dessous). Les hyperplans de séparations sont déterminés par rapport aux barycentres des différentes classes. En d’autres termes, ils sont placés à égale distance des centres de gravité des différents nuages de points dans la représentation en composantes principales de l’ADL.
À partir de là, l’espace est divisé en plusieurs régions dont les frontières son linéaires. Chaque région correspond à une classe. Il suffit alors de projeter des nouveaux individus dans cet espace (recalcul des coordonnées selon la rotation du système d’axes et représentation de ces coordonnées dans l’espace des individus de l’ADL). Nous regardons alors dans quelle sous-région nos points ont été se placer pour en déterminer la classe à laquelle ils appartiennent. Pour une autre explication, voyez ici.
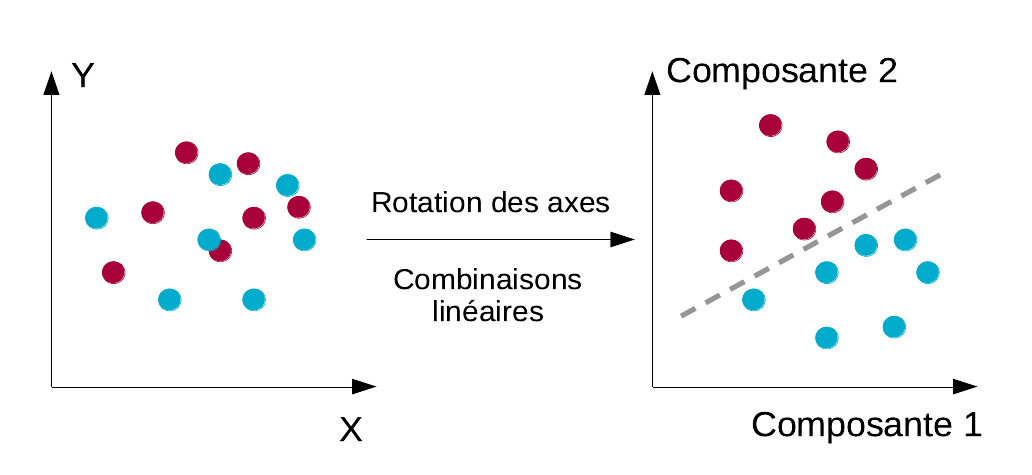
Schéma de principe de rotation du système d’axes de l’ADL afin de maximiser la variance inter-groupe, et donc, de séparer au mieux ces groupes dans le nouveau système d’axe. La séparation du plan à l’aide d’une droite à égale distance des barycentres des groupes définit des sous-régions qui correspondent à chacune des classes.
Cet algorithme présente l’avantage d’être simple et rapide à calculer. Par contre, l’ADL n’est généralement pas la méthode la plus performante en classification supervisée, et elle impose que les différents groupes soient décrits par des sous-espaces uniques et délimités par des hyperplans dans l’hyperespace des p variables initiales, soit, une hypothèse de départ très forte. Il est possible de restreindre l’outil de reconnaissance à q < p composantes discriminantes principales, afin de simplifier et d’accélérer le calcul, si cela s’avère nécessaire (les détails sortent du cadre de ce cours).
1.3.1 Manchots antarctiques
Partons d’un exemple pratique sur trois populations de manchots adultes proches de la station de recherche PALMER en Antarctique.
La fonction skim() nous donne un aperçu du contenu de ce jeu de données. Si vous voulez des informations supplémentaires, consultez la page d’aide du jeu de données ou palmerpenguins.
| Name | penguins |
| Number of rows | 344 |
| Number of columns | 8 |
| _______________________ | |
| Column type frequency: | |
| factor | 3 |
| numeric | 5 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| species | 0 | 1.00 | FALSE | 3 | Ade: 152, Gen: 124, Chi: 68 |
| island | 0 | 1.00 | FALSE | 3 | Bis: 168, Dre: 124, Tor: 52 |
| sex | 11 | 0.97 | FALSE | 2 | mal: 168, fem: 165 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| bill_length_mm | 2 | 0.99 | 43.92 | 5.46 | 32.1 | 39.23 | 44.45 | 48.5 | 59.6 | ▃▇▇▆▁ |
| bill_depth_mm | 2 | 0.99 | 17.15 | 1.97 | 13.1 | 15.60 | 17.30 | 18.7 | 21.5 | ▅▅▇▇▂ |
| flipper_length_mm | 2 | 0.99 | 200.92 | 14.06 | 172.0 | 190.00 | 197.00 | 213.0 | 231.0 | ▂▇▃▅▂ |
| body_mass_g | 2 | 0.99 | 4201.75 | 801.95 | 2700.0 | 3550.00 | 4050.00 | 4750.0 | 6300.0 | ▃▇▆▃▂ |
| year | 0 | 1.00 | 2008.03 | 0.82 | 2007.0 | 2007.00 | 2008.00 | 2009.0 | 2009.0 | ▇▁▇▁▇ |
Ce jeu de données comprend 8 variables et 344 individus. La variable que nous cherchons à prédire ici est species (variable réponse). Trois espèces de manchots sont étudiées :
- Adelie (152 individus)
- Gentoo (124 individus)
- Chinstrap (68 individus)
Bien que nous n’ayons pas un plan balancé (même nombre d’items pour chaque niveau de notre variable réponse), les différences restent encore acceptables, soit un peu plus du simple au double entre Chinstrap et Adelie. Nous pourrions sous-échantillonner les espèces les plus abondantes mais nous diminuons alors la taille de notre jeu de données. Des techniques existent pour balancer le nombre d’items, dont la plus en vogue : SMOTE (“Synthetic Minority Over-sampling”). Elle peut s’avérer utile ici, mais nous poursuivrons sans modifier artificiellement le nombre d’items dans notre jeu de données.
En quoi un nombre différent d’items dans chaque classe peut-il poser problème en classification supervisée ? En fait comme la plupart des critères sont basés sur la fraction correcte prédite pour l’ensemble des données, en cas de différences extrêmes nous pourrions arriver à des situations paradoxales. Imaginez par exemple une maladie très rare. Nous avons un échantillon important de patients sains, mais forcément très peu de cas positifs. Par exemple, 1,5% de notre set d’apprentissage est constitué de patients malades. Dans ce cas, un classifieur trivial qui classerait tout le monde comme sain ferait globalement 98,5% de prédictions correctes. C’est difficile à battre, et en même temps pas très utile. Donc, deux points à retenir de ce cas fictif :
Toujours essayer de balancer les items dans les classes, mais sans exagaration (une différence du simple au double est encore gérable, pour fixer les idées),
Le point de référence pour définir si un classifieur est efficace dépend de la classe la plus abondante. Avec un plan balancé à deux classes, un classiifieur qui classe correctement 70% des items fait 20% mieux que le classement au hasard. Par contre, si la classe la plus abondante représente 75% du set, il fera moins bien de 5% qu’un classement purement au hasard (sic !)
On observe la présence de quelques données manquantes que nous supprimerons plus loin avant de faire notre analyse. Nous allons également renommer et donner un labels à nos variables quantitatives (nos attributs).
penguins <- rename(
penguins, bill_length = bill_length_mm, bill_depth = bill_depth_mm,
flipper_length = flipper_length_mm, body_mass = body_mass_g)
penguins <- labelise(penguins,
label = list(
species = "Espèce", island = "Île", bill_length = "Longueur du bec",
bill_depth = "Épaisseur du bec", flipper_length = "Longueur des nageoires",
body_mass = "Masse", sex = "Sexe", year = "Année de la mesure"),
units = list(
bill_length = "mm", bill_depth = "mm", flipper_length = "mm",
body_mass = "g"))Nous nous intéressons uniquement pour l’instant aux variables explicatives numériques, et nous éliminons également les lignes du tableau qui contiennent des valeurs manquantes.
drop_na() est bien pratique pour obtenir un tableau de données propre sans aucunes valeurs manquantes. Cependant, elle est assez impitoyable : toute ligne du tableau qui contient au moins une valeur manquante est éliminée. Toujours sélectionner les valeurs que l’on veut retenir dans le modèle avant de l’appliquer, sinon, on retirera aussi des lignes pour lesquelles les variables qui ne nous intéressent pas ont aussi des valeurs manquantes (ici, le sexe).
Le graphique ci-dessous propose un nuage de points pour différencier ces trois espèces selon seulement deux variables. On observe une répartition assez bonne entre nos trois espèces pour les deux variables représentées. Ce graphique nous laisse penser que l’algorithme de classification a de grandes chances d’être efficace pour séparer ces trois espèces, car le jeu de donnée montre une tendance claire. N’oublions pas que nous avons au total quatre attributs à disposition.
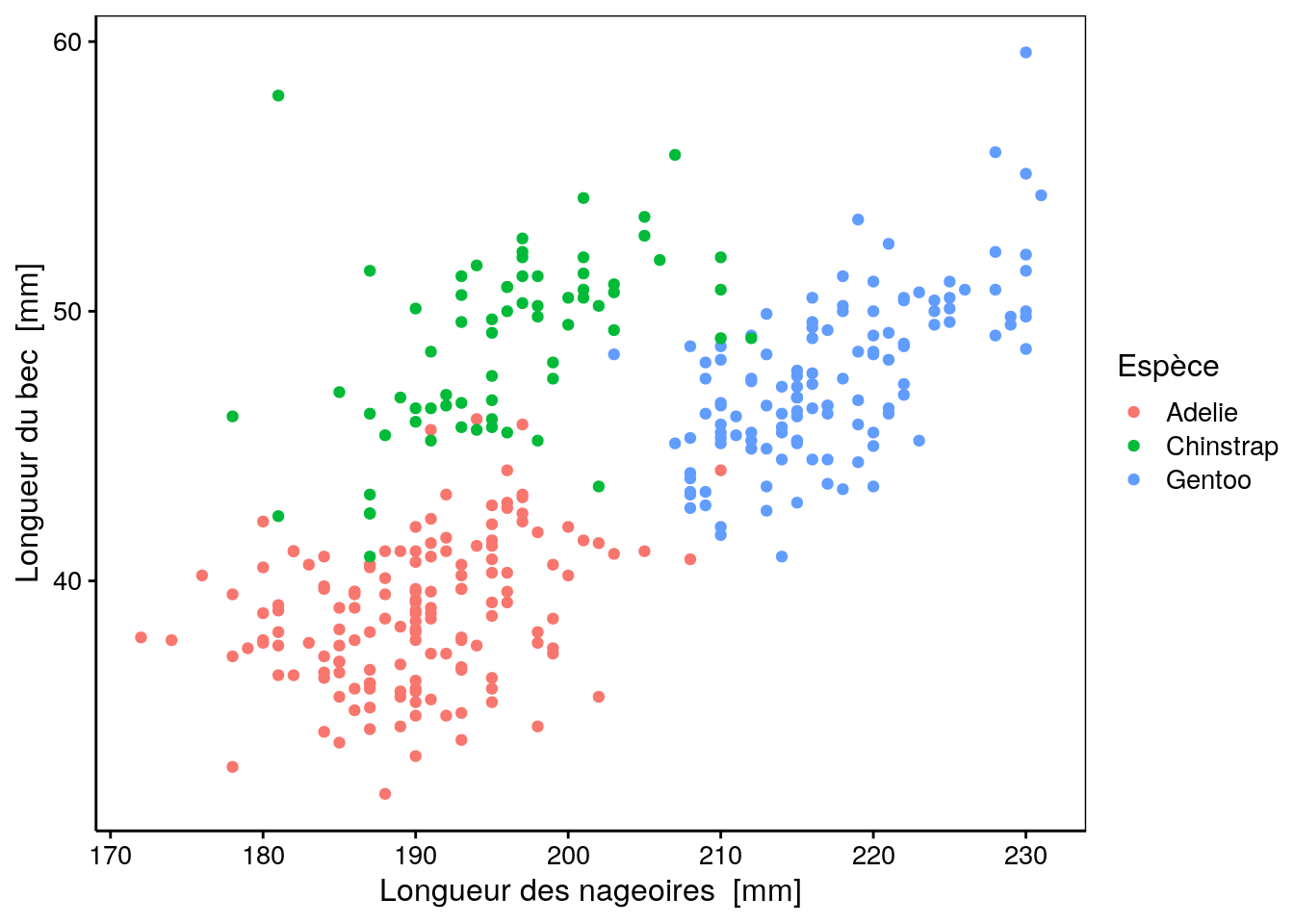
N’hésitez pas à explorer par vous-même ce jeu de données : il y a en effet pas mal de graphiques intéressants à réaliser avant de se lancer dans une analyse plus approfondie… qui a dit “boites à moustaches” ? J’ai entendu “matrice de corrélation” là-bas au fond ? …
Le jeu de données est découpé en un set d’apprentissage et un set de test. On décide de garder 2/3 des observations pour le set d’apprentissage.
# [1] 228Nous séparons nos observations en deux sets indépendants. Nouys utilisons cependant la fonction set.seed() afin de fixer le début du générateur de nombres pseudo-aléatoires, ce qui donne une série de nombres qui ont les mêmes propriétés que des nombres tirés au sort, mais ce tirage au sort est reproductible d’une fois à l’autre.
set.seed(324)
# Récupération de n_learning items parmi les numéros de lignes de 1 à n
learning <- sample(1:n, n_learning)
# Sous-tableau correspondant à ces lignes -> apprentissage
penguins_learn <- penguins[learning, ]
# Sous-tableau ne correspondant pas à ces lignes -> test
penguins_test <- penguins[-learning, ]Le set d’apprentissage comprend 228 items et le set de test comprend 114 individus.
1.3.1.1 Apprentissage avec ADL
Nous utilisons le package {mlearning} pour réaliser notre analyse ici. La fonction mlLda() propose une structure que nous avons déjà employée à de nombreuses reprises. Il faut fournir le set d’apprentissage (data =) et la formule. Dans notre cas, nous souhaitons prédire l’espèce à l’aide de plusieurs attributs.
library(mlearning)
penguins_lda <- mlLda(data = penguins_learn,
species ~ bill_length + bill_depth + flipper_length + body_mass)Cependant dans le cas particulier où toutes les variables du tableau sont utilisées pour l’analyse, comme c’est le cas ici, la formule peut être abrégée en class ~ ., ce qui signifie que la variable dépendante qualitative class est étudiée en fonction de toutes les autres variables du tableau, considérées toutes comme des attributs. En fait, ce n’est pas tout-à-fait synonyme car dans ce dernier cas, les fonction du package {mlearning} utilisent des astuces de programmation pour optimiser les calculs (autant en vitesse qu’en utilisation de la mémoire vive). Il est donc très fortement conseillé d’utiliser cette forme.
# Utilisation de la forme condensée de notre formule
penguins_lda <- mlLda(data = penguins_learn, species ~ .)
penguins_lda# A mlearning object of class mlLda (linear discriminant analysis):
# Call: mlLda.formula(formula = species ~ ., data = penguins_learn)
# Trained using 228 cases:
# Adelie Chinstrap Gentoo
# 102 42 84Nous pouvons visualiser nos données selon les deux premiers axes discriminants (notés LD1 et LD2) à l’aide du graphique suivant :
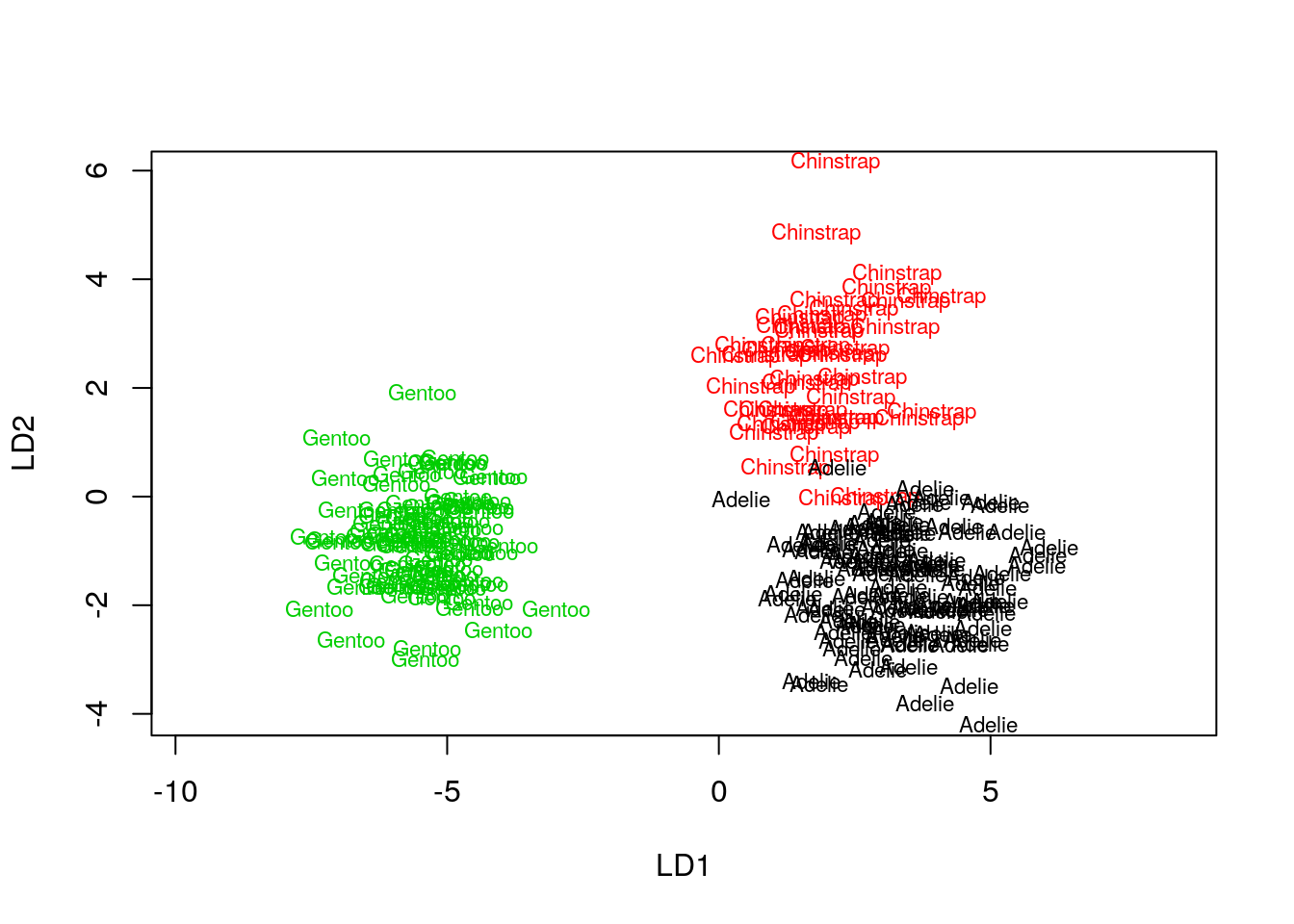
Nous voyons bien que la séparation est très bonne. Gentoo est très clairement séparé des deux autres, tandis que la frontière entre Chnistrap et Adelie est un peu moins nette, mais toutefois clairement visible.
Visualisation des sous-régions correspondant aux trois espèces dans un plan.
Bien que {mlearning} ne propose aucune fonction pour visualiser le découpage que réalise l’ADL pour décider à quelle classe un point appartient, nous pouvons la créer avec un peu de code en R (les détails de cette fonction vont au delà de ce cours, mais si vous êtes curieux, vous pouvez inspecter le code pour comprendre comment elle fonctionne).
Pour visualiser ce qui se passe dans un plan à deux dimensions, nous allons refaire une prédiction à l’aide de deux variables seulement :
penguins_learn %>.%
select(., flipper_length, bill_length, species) -> penguins_learn2
penguins_lda2 <- mlLda(data = penguins_learn2, species ~ .)
summary(penguins_lda2)# A mlearning object of class mlLda (linear discriminant analysis):
# Initial call: mlLda.formula(formula = species ~ ., data = penguins_learn2)
# Call:
# lda(sapply(train, as.numeric), grouping = response, .args. = ..1)
#
# Prior probabilities of groups:
# Adelie Chinstrap Gentoo
# 0.4473684 0.1842105 0.3684211
#
# Group means:
# flipper_length bill_length
# Adelie 190.5784 38.68235
# Chinstrap 197.3810 49.15714
# Gentoo 217.0357 47.32381
#
# Coefficients of linear discriminants:
# LD1 LD2
# flipper_length 0.1095092 0.1208877
# bill_length 0.1390529 -0.3486817
#
# Proportion of trace:
# LD1 LD2
# 0.7268 0.2732Nous voyons que 70% de la variance inter-classe est sur LD1 et 30% sur LD2. Un partitionnement dans le plan des variables de départ est obtenu comme suit :
# predplot() function inspired from MASS, chap. 12, p. 340
predplot <- function(object, main = "", len = 100, ...) {
pen_data <- as.data.frame(penguins_learn2)
plot(pen_data[, 1], pen_data[, 2], type = "n", #log = "xy",
xlab = "longueur des nageoires [mm]", ylab = "longueur du bec [mm]", main = main)
for (il in 1:3) {
set <- pen_data$species == levels(pen_data$species)[il]
text(pen_data[set, 1], pen_data[set, 2],
labels = substr(as.character(pen_data$species[set]), 1, 3), col = 1 + il)
}
xp <- seq(170, 235, length = len)
yp <- seq(30, 60, length = len)
penT <- expand.grid(flipper_length = xp, bill_length = yp)
Z <- predict(object, penT, type = "both",...)
zp <- as.numeric(Z$class)
zp <- Z$membership[, 3] - pmax(Z$membership[, 2], Z$membership[, 1])
contour(xp, yp, matrix(zp, len), add = TRUE, levels = 0, labex = 0)
zp <- Z$membership[, 1] - pmax(Z$membership[, 2], Z$membership[, 3])
contour(xp, yp, matrix(zp, len), add = TRUE, levels = 0, labex = 0)
invisible()
}
predplot(penguins_lda2)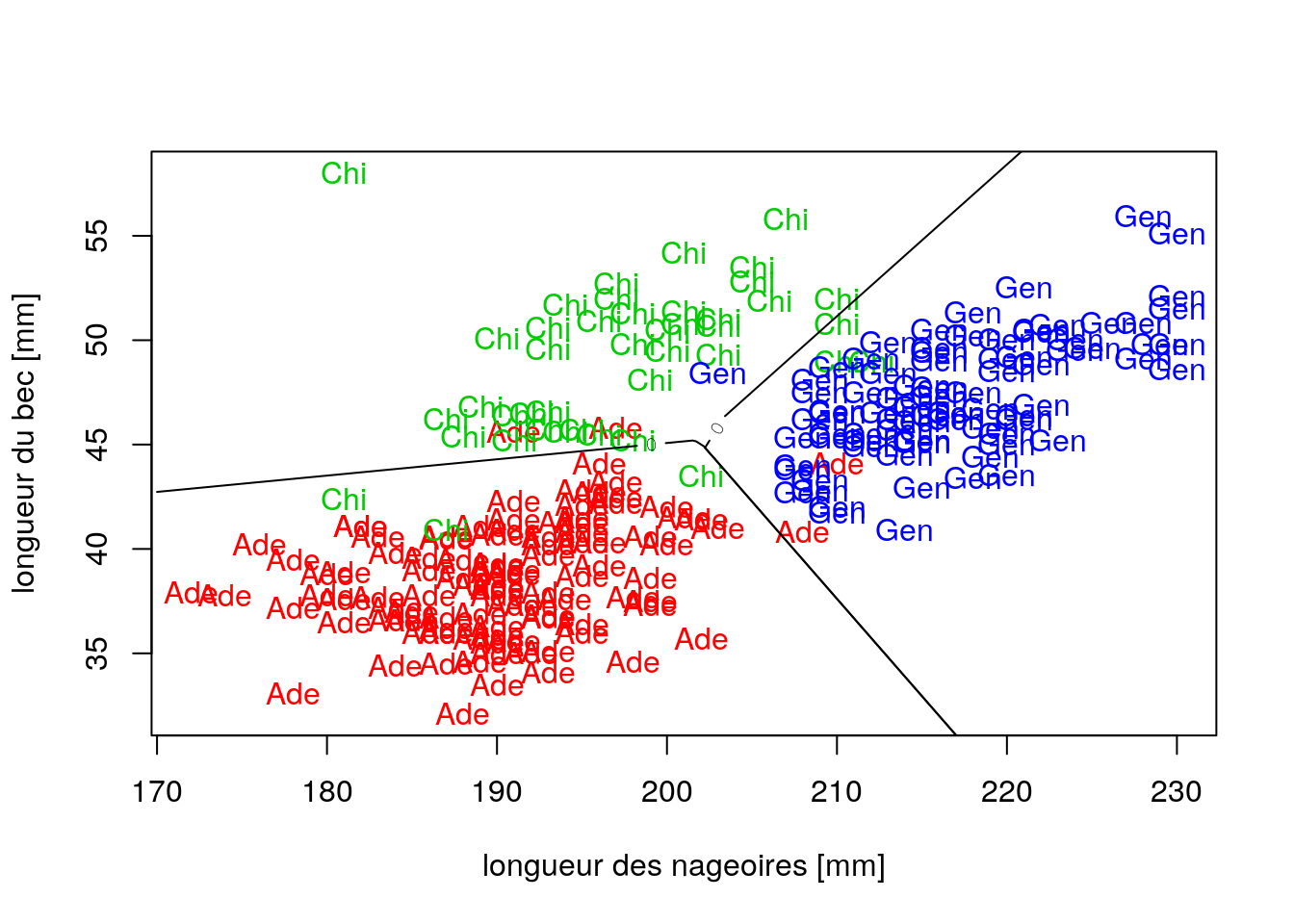
Effectivement, nous distinguons clairement que le plan a été divisé en 3 parties séparées par des segments de droites pour en délimiter les fromtières.
1.3.1.2 Phase de test
Nous allons maintenant vérifier les performances de ce classifieur à l’aide de la matrice de confusion et des métriques que nous pouvons en dériver. Nous commençons par prédire les classes de notre set de test avec notre objet penguins_lda (fonction predict() tout simplement). Si elle est appliquée sur l’objet classifieur sans aucun autre argument, ce sont les items du set d’apprentissage qui sont classés, sinon, on rajoute comme second argument le nom du tableau (de test par exemple).
# [1] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [8] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [15] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [22] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [29] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [36] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [43] Adelie Adelie Adelie Adelie Adelie Adelie Adelie
# [50] Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo
# [57] Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo
# [64] Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo
# [71] Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo
# [78] Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo Gentoo
# [85] Gentoo Gentoo Gentoo Gentoo Chinstrap Chinstrap Chinstrap
# [92] Chinstrap Chinstrap Chinstrap Chinstrap Chinstrap Chinstrap Chinstrap
# [99] Chinstrap Chinstrap Chinstrap Chinstrap Chinstrap Adelie Chinstrap
# [106] Chinstrap Chinstrap Chinstrap Chinstrap Chinstrap Adelie Chinstrap
# [113] Chinstrap Chinstrap
# Levels: Adelie Chinstrap GentooCet object contient donc les 114 prédictions réalisées par notre classifieur. Nous réalisons un tableau de contingence à double entrée en croisant ces données avec les espèces déterminées par les spécialistes qui se trouvent dans la variables species de notre set de test (que la classifieur n’a, bien entendu pas utilisé pour faire ses prédictions). Dans le langage de la classification supervisée, ce tableau de contingence à double entrée s’appelle une matrice de confusion donc, et c’est un excellent outil pour étudier les performances de notre classifieur.
# Argument 1: prédictions, argument 2: valeurs connues pour `species`
penguins_conf <- confusion(penguins_pred, penguins_test$species)
penguins_conf# 114 items classified with 112 true positives (error rate = 1.8%)
# Predicted
# Actual 01 02 03 (sum) (FNR%)
# 01 Gentoo 39 0 0 39 0
# 02 Adelie 0 49 0 49 0
# 03 Chinstrap 0 2 24 26 8
# (sum) 39 51 24 114 2La fonction plot() appliquée à notre objet penguins_conf de classe confusion nous donne une présentation visuelle colorée plus facile à lire que le tableau textuel brut (pensez à des cas plus complexes avec beaucoup plus de classes).
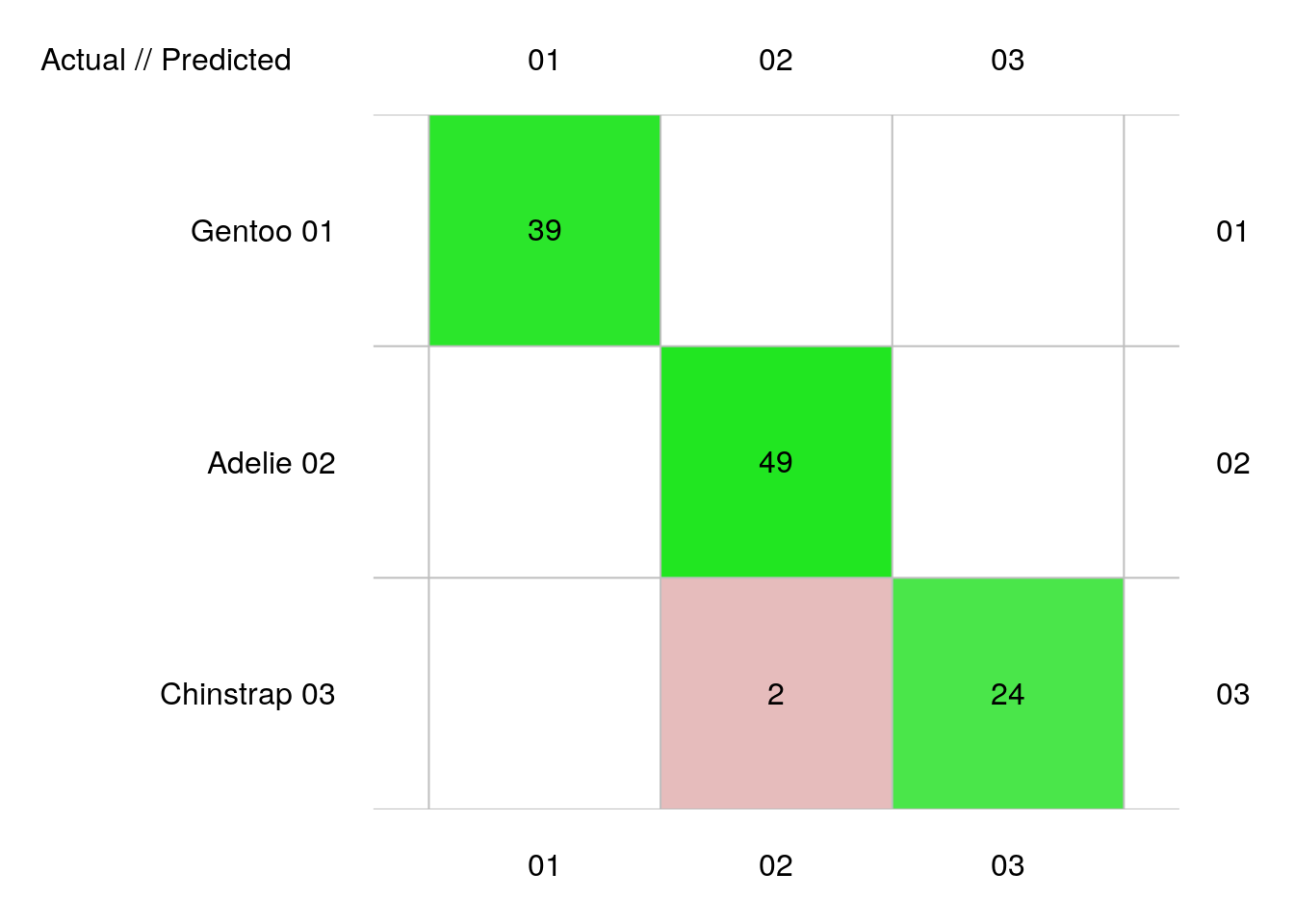
Notre classifieur a commis deux erreurs sur les données du set de test. Il semble que Gentoo puisse s’identifier sans erreurs par rapport aux deux autres espèces, alors qu’une erreur (faible) subsiste dans la discrimination entre Adelie et Chinstrap. On obtient tout le détail des métriques que nous avons vu précédemment en faisant appel à la fonction summary().
# 114 items classified with 112 true positives (error = 1.8%)
#
# Global statistics on reweighted data:
# Error rate: 1.8%, F(micro-average): 0.981, F(macro-average): 0.98
#
# Fscore Recall Precision Specificity NPV FPR
# Gentoo 1.00 1.0000000 1.0000000 1.0000000 1.0000000 0.00000000
# Adelie 0.98 1.0000000 0.9607843 0.9692308 1.0000000 0.03076923
# Chinstrap 0.96 0.9230769 1.0000000 1.0000000 0.9777778 0.00000000
# FNR FDR FOR LRPT LRNT LRPS LRNS
# Gentoo 0.00000000 0.00000000 0.00000000 Inf 0.00000000 Inf 0.00000000
# Adelie 0.00000000 0.03921569 0.00000000 32.5 0.00000000 Inf 0.03921569
# Chinstrap 0.07692308 0.00000000 0.02222222 Inf 0.07692308 45 0.00000000
# BalAcc MCC Chisq Bray Auto Manu A_M TP FP FN TN
# Gentoo 1.0000000 1.0000000 114.0000 0.00000000 39 39 0 39 0 0 75
# Adelie 0.9846154 0.9649983 106.1593 0.00877193 51 49 2 49 2 0 63
# Chinstrap 0.9615385 0.9500337 102.8923 0.00877193 24 26 -2 24 0 2 88À vous de jouer !
Effectuez maintenant les exercices du tutoriel C01Lb_lda (Analyse discriminante linéaire).
BioDataScience3::run("C01Lb_lda")Pièges et astuces
Tout comme cela avait déjà été expliqué lors de la présentation de l’ ACP, il est crucial de bien nettoyer son jeu de données avant de réaliser une ADL. Il est également très important de vérifier que les relations entre les variables prédictives (les attributs) sont linéaires dans le cas de l’analyse disciminante linéaire. Sinon il faut transformer les données de manière appropriée. Rappelez-vous que l’ADL s’intéresse aux corrélations linéaires entre vos variables.
1.3.1.3 Déploiement
Notre jeu de données ne reprenait que les données du set d’apprentissage et du set de test. Néanmoins, les scientifiques qui ont utilisé ces données pourraient légitimement considérer que le classifieur est suffisamment fiable pour pouvoir classer les trois espèces de manchots sur base des quatre mesures effectuées sur n’importe quel individu. Ainsi, s’ils possèdent par ailleurs des données biométriques sur les manchots de la région pour lesquelles il manque l’identification de l’espèce, ils pourraient utiliser leur classifieur pour les prédire. Si le jeu de donnée biométrique s’appelle par exemple palmer2data, ils feront tout simplement predict(penguins_lda, palmer2data) pour obtenir une prédiction des espèces de manchots pour les individus repris dans palmer2data.
À vous de jouer !
Réalisez l’assignation C01Ga_ml1, partie I.
Si vous êtes un utilisateur non enregistré ou que vous travaillez en dehors d’un cours, faites un “fork” de ce dépôt.
Voyez les explications dans le fichier README.md, partie I.