1.2 Régression linéaire simple
Nous allons découvrir les bases de la régression linéaire de façon intuitive. Nous utilisons le jeu de données trees qui rassemble la mesure du diamètre, de la hauteur et du volume de bois de cerisiers noirs.
# importation des données
trees <- read("trees", package = "datasets", lang = "fr")Rapellons-nous que dans le chapitre 12 du livre science des données 1, nous avons étudié l’association de deux variables quantitatives (ou numériques). Nous utilisons donc une matrice de corrélation afin de mettre en évidence la corrélation entre nos trois variables qui composent le jeu de donnée trees.
La fonction correlation() nous renvoie un tableau de la matrice de correlation avec l’indice de Pearson (corrélation linéaire) par défaut. C’est précisement ce coefficient qui nous intéresse dans le cadre d’une régression linéaire comme description préalable des données autant que pour nous guider dans le choix de nos variables.
(trees_corr <- correlation(trees))# Matrix of Pearson's product-moment correlation:
# (calculation uses everything)
# diameter height volume
# diameter 1.000 0.519 0.967
# height 0.519 1.000 0.597
# volume 0.967 0.597 1.000Nous pouvons également observer cette matrice sous la forme d’un graphique plus convivial.
plot(trees_corr, type = "lower")
Cependant, n’oubliez pas qu’il est indispensable de visualiser les nuages de points pour ne pas tomber dans le piège mis en avant par le jeu de données artificiel appelé “quartet d’Anscombe” qui montre très bien comment des données très différentes peuvent avoir même moyenne, même variance et même coefficient de corrélation. Un graphique de type matrice de nuages de points est tout indiqué ici.
GGally::ggscatmat(as.data.frame(trees), 1:3)
Nous observons une plus forte corrélation linéaire entre le volume et le diamètre. Intéressons nous à cette association.
chart(trees, volume ~ diameter) +
geom_point()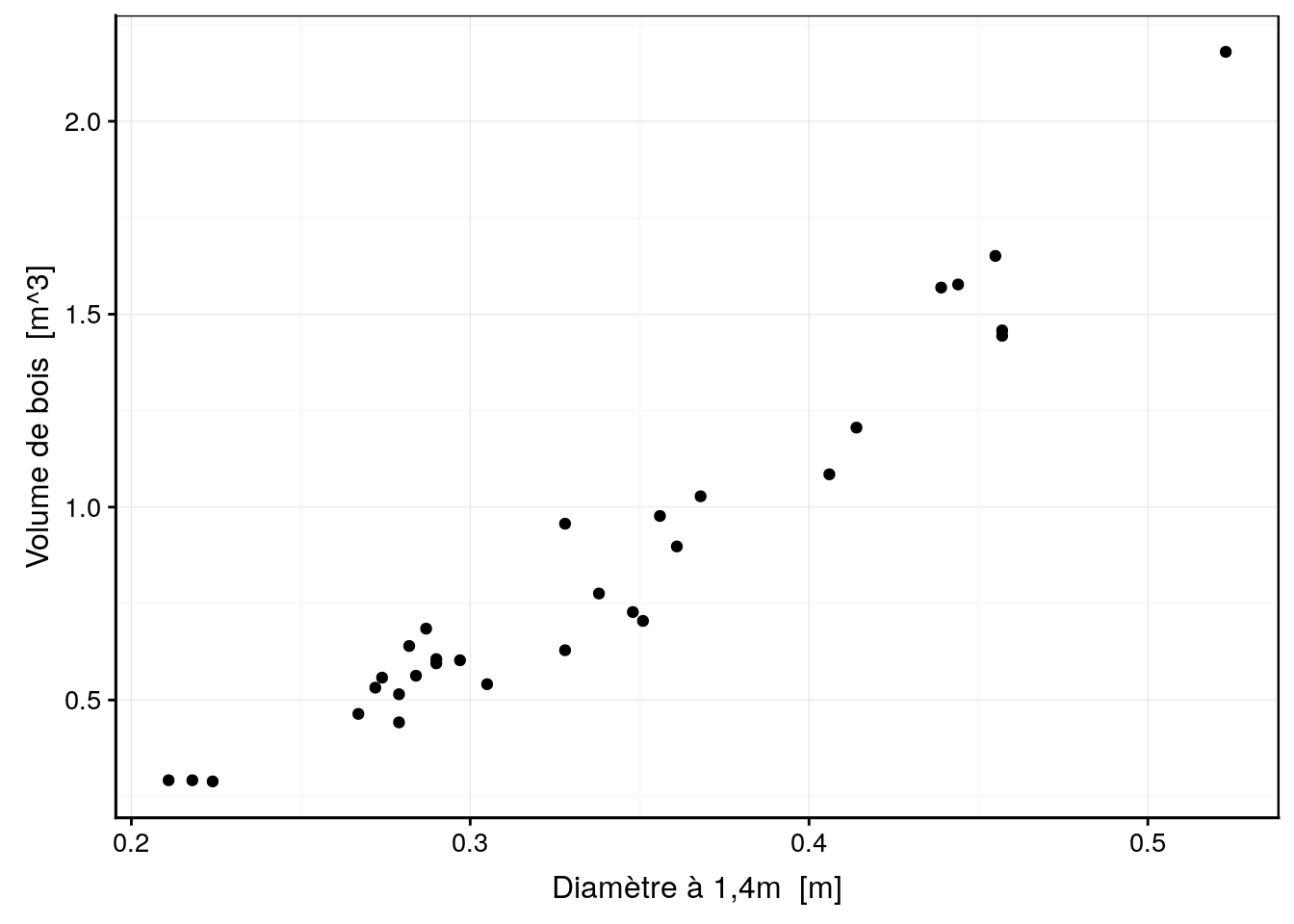
Si vous deviez ajouter une droite permettant de représenter au mieux les données, où est ce que vous la placeriez ?
Pour rappel, une droite respecte l’équation mathématique suivante :
\[y = a \ x + b\]
dont a est la pente (slope en anglais) et b est l’ordonnée à l’origine (intercept en anglais).
# Sélection de pentes et d'ordonnées à l'origine
models <- tibble(
model = paste("model", 1:4, sep = "-"),
slope = c(5, 5.5, 6, 0),
intercept = c(-0.5, -0.95, -1.5, 0.85)
)
chart(trees, volume ~ diameter) +
geom_point() +
geom_abline(data = models,
aes(slope = slope, intercept = intercept, color = model)) +
labs( color = "Modèle")
Nous avons quatre droites candidates pour représenter au mieux les observations. Quel est la meilleure d’entre elles selon vous ?
1.2.1 Quantifier l’ajustement d’un modèle
Nous voulons identifier la meilleure régression, c’est-à-dire la régression le plus proche de nos données. Nous avons besoin d’une règle qui va nous permettre de quantifier la distance de nos observations à notre modèle afin d’obtenir la régression avec la plus faible distance possible de l’ensemble de nos observations.
Décomposons le problème étape par étape et intéressons nous au model-1 (droite en rouge sur le graphique précédent).
- Calculer les valeurs de \(y_i\) prédites par le modèle que nous noterons par convention \(\hat y_i\) (prononcez “y chapeau” ou “y hat” en anglais) pour chaque observation \(i\).
# Calculer la valeur de y pour chaque valeur de x suivant le model souhaité
# Création de notre fonction
model <- function(slope, intercept, x) {
prediction <- intercept + slope * x
attributes(prediction) <- NULL
prediction
}
# Application de notre fonction
yhat <- model(slope = 5, intercept = -0.5, x = trees$diameter)
# Affichage des résultats
yhat# [1] 0.555 0.590 0.620 0.835 0.860 0.870 0.895 0.895 0.910 0.920 0.935
# [12] 0.950 0.950 0.985 1.025 1.140 1.140 1.190 1.240 1.255 1.280 1.305
# [23] 1.340 1.530 1.570 1.695 1.720 1.775 1.785 1.785 2.115- Calculer la distance entre les observations \(y_i\) et les prédictions par notre modèle \(\hat y_i\), soit \(y_i - \hat y_i\)
Les distances que nous souhaitons calculer, sont appelées les résidus du modèle et sont notés \(\epsilon_i\) (epsilon). Nous pouvons premièrement visualiser ces résidus graphiquement (ici en rouge par rapport à model-1) :

Nous pouvons ensuite facilement calculer leurs valeurs comme ci-dessous :
# Calculer la distance entre y et y barre
# Création de notre fonction de calcul des résidus
distance <- function(observations, predictions) {
residus <- observations - predictions
attributes(residus) <- NULL
residus
}
# Utilisation de la fonction
resid <- distance(observations = trees$volume, predictions = yhat)
# Impression des résultats
resid# [1] -0.263 -0.298 -0.331 -0.371 -0.328 -0.312 -0.453 -0.380 -0.270 -0.357
# [11] -0.250 -0.355 -0.344 -0.382 -0.484 -0.511 -0.183 -0.414 -0.512 -0.550
# [21] -0.303 -0.407 -0.312 -0.445 -0.364 -0.126 -0.143 -0.124 -0.327 -0.341
# [31] 0.065- Définir une règle pour obtenir une valeur unique qui résume l’ensemble des distances de nos observations par rapport aux prédictions du modèle. Une première idée serait de sommer l’ensemble de nos résidus comme ci-dessous :
sum(resid)# [1] -10.175Appliquons ces calculs sur nos quatre modèles afin de les comparer… Le modèle pour lequel notree critère serait le plus proche de zéro serait alors considéré comme le meilleur.
| model-1 | model-2 | model-3 | model-4 |
|---|---|---|---|
| -10.175 | -1.441 | 10.393 | 0.135 |
Selon notre méthode, il en ressort que le modèle 4 est le plus approprié pour représenter au mieux nos données. Qu’en pensez vous ?

Intuitivement, nous nous aperçevons que le modèle 4 est loin d’être le meilleur. Nous pouvons en déduire que la somme des résidus n’est pas un bon critère pour ajuster un modèle linéaire.
Le problème lorsque nous sommons des résidus, est la présence de résidus positifs et de résidus négatifs (ici par rapport à model-4).

Ainsi avec notre première méthode naïve de somme des résidus, il suffit d’avoir autant de résidus positifs que négatifs pour avoir un résultat proche de zéro. Mais cela n’implique pas que les observations soient prochent de la droite pour autant. Avez-vous une autre idée que de sommer les résidus ?
- Sommer le carré des résidus aurait des propriétés intéressantes car d’une part les carrés de nombres positifs et négatifs sont tous positifs, et d’autre part, plus une observation est éloignée plus sa distance au carré pèse fortement dans la somme2.
Nous obtenons les résultats suivants :
| model-1 | model-2 | model-3 | model-4 |
|---|---|---|---|
| 3.842211 | 0.4931095 | 3.929195 | 6.498511 |
- Sommer les valeurs absolues des résidus mène également à des contributions toutes positives, mais sans pénaliser outre mesure les observations les plus éloignées.
Nous obtenons les résultats suivants :
| model-1 | model-2 | model-3 | model-4 |
|---|---|---|---|
| 10.305 | 3.186 | 10.393 | 11.525 |
Nous avons trouvé deux solutions intéressantes pour quantifier la distance de notre droite par rapport à nos observations. En effet, dans les deux cas, la valeur minimale est obtenue pour le model-2 (en vert sur le graphique) qui est visuellement le meilleur des quatre.
La méthode utilisant les carrés des résidus s’appelle une régression par les moindres carrés. Notre objectif est donc de trouver les meilleures valeurs des paramètres \(a\) et \(b\) de la droite pour minimiser ce critère. Il en résulte une fonction dite objective qui dépend de \(x\) et de nos paramètres \(a\) et \(b\) à minimiser. Cette approche s’appelle la régression par les moindres carrés et elle est la plus utilisée.
L’approche utilisant la somme de la valeur absolue des résidus est également utilisable (et elle est d’ailleurs préférable en présence de valeurs extrêmes potentiellement suspectes). Elle s’apppelle régression par la médiane, un cas particulier de la régression quantile, une approche intéressante dans le cas de non normalité des résidus et/ou de présence de valeurs extrêmes suspectes.1.2.2 Trouver la meilleure droite
Essayez de trouver le meilleur modèle par vous-même dans une application interactive “shiny”. Démarrez la SciViews Box et RStudio. Dans la fenêtre Console de RStudio, entrez l’instruction suivante suivie de la touche Entrée pour ouvrir l’application :
BioDataScience2::app("01a_lin_mod") # TODOMéthode alternative :
shiny::runApp(system.file("shiny/01a_lin_mod", package = "BioDataScience2"))ESC pour reprendre la main dans R lorsque vous aurez fini avec l’application shiny.
Nous pouvons nous demander si notre modèle 2 qui est la meilleure droite de nos quatre modèles est le meilleur modèle possible dans l’absolu. Pour se faire nous allons devoir définir unez technique d’optimisation qui nous permet de déterminer quelle est la droite qui minimise notre fonction objective. Dans la suite, nous garderonsq le critère des moindres carrés (des résidus).
Imaginons que nous n’avons pas quatre mais 5000 modèles linéaires avec des pentes et des ordonnées à l’origine différentes. Quelle est la meilleure droite ?
set.seed(34643)
models1 <- tibble(
intercept = runif(5000, -5, 4),
slope = runif(5000, -5, 15))
chart(trees, volume ~ diameter) +
geom_point() +
geom_abline(aes(intercept = intercept, slope = slope),
data = models1, alpha = 1/6) 
Nous voyons sur le graphique qu’un grand nombre de droites différentes sont testées, mais nous ne distinguons pas grand chose de plus. Cependant, sur ces 5000 modèles, nous pouvons maintenant calculer la somme des carrés des résidus et ensuite déterminer quel est le meilleur d’entre eux.
# Fonction de calcul de la somme des carrés des résidus
measure_distance <- function(slope, intercept, x, y) {
ybar <- x * slope + intercept
resid <- y - ybar
sum(resid^2)
}
# Test de la fonction
#measure_distance(slope = 0, intercept = 0.85, x = trees$diameter, y = trees$volume)
# Fonction adaptée pour être employé avec purrr:map() pour distribuer le calcul
trees_dist <- function(intercept, slope) {
measure_distance(slope = slope, intercept = intercept,
x = trees$diameter, y = trees$volume)
}
models1 <- models1 %>%
mutate(dist = purrr::map2_dbl(intercept, slope, trees_dist))Si nous réalisons un graphique de valeurs de pentes, d’ordonnées à l’origine et de la valeur de la fonction objective (distance) en couleur, nous obtenons le graphique ci-dessous.
plot <- chart(models1, slope ~ intercept %col=% dist) +
geom_point() +
geom_point(data = filter(models1, rank(dist) <= 10),
shape = 1, color = 'red', size = 3) +
labs( y = "Pente", x = "Ordonnée à l'origine", color = "Distance") +
scale_color_viridis_c(direction = -1)
plotly::ggplotly(plot)Les 10 valeurs les plus faibles sont mises en évidence sur le graphique par des cercles rouges. Le modèle optimal que nous recherchons se trouve dans cette région.
best_models <- models1 %>.%
filter(., rank(dist) <= 10)Nous pouvons afficher les 10 meilleurs modèles sur notre graphique :
chart(trees, volume ~ diameter) +
geom_abline(data = best_models,
aes(slope = slope, intercept = intercept, color = dist), alpha = 3/4) +
geom_point() +
labs(color = "Distance") +
scale_color_viridis_c(direction = -1)
En résumé, nous avons besoin d’une fonction qui calcule la distance d’un modèle par rapport à nos observations et d’un algorithme pour la minimiser.
Il n’est cependant pas nécessaire de chercher pendant des heures la meilleure fonction et le meilleur algorithme. Il existe dans R, un outil spécifiquement conçu pour adapter des modèles linéaires sur des observations, la fonction lm(). Dans le cas particulier de la régression par les moindres carrés, la solution s’obtient très facilement par un simple calcul :
\[a = \frac{cov_{x, y}}{var_x} \ \ \ \textrm{et} \ \ \ b = \bar y - a \ \bar x\]
où \(\bar x\) et \(\bar y\) sont les moyennes pour les deux variables, \(cov\) est la covariance et \(var\) est la variance.
..., ensuite choisissez models, ensuite models : linear et choisissez le snippet qui vous convient dans la liste.
(lm. <- lm(data = trees, volume ~ diameter))#
# Call:
# lm(formula = volume ~ diameter, data = trees)
#
# Coefficients:
# (Intercept) diameter
# -1.047 5.652Nous pouvons reporter ces valeurs sur notre graphique afin d’observer ce résultat par rapport à nos modèles aléatoires. nous avons en rouge la droite calculée par la fonction lm().
chart(trees, volume ~ diameter) +
geom_abline(data = best_models,
aes(slope = slope, intercept = intercept, color = dist), alpha = 3/4) +
geom_point() +
geom_abline(
aes(intercept = lm.$coefficients[1], slope = lm.$coefficients[2]),
color = "red", size = 1.5) +
labs( color = "Distance") +
scale_color_viridis_c(direction = -1)
1.2.3 La fonction lm()
Suite à notre découverte de manière intuitive de la régression linéaire simple, nous pouvons récapituler quelques points clés :
- Une droite suit l’équation mathématique suivante :
\[y = a \ x + b\] dont \(a\) est la pente (slope en anglais) et \(b\) est l’ordonnée à l’origine (intercept en anglais), tous deux les paramètres du modèle, alors que \(x\) et \(y\) en sont les variables.
- La distance entre une valeur observée \(y_i\) et une valeur prédite \(\hat y_i\) se nomme le résidu (\(\epsilon_i\)) et se mesure toujours parallèlement à l’axe \(y\). Cela revient à considérer que toute l’erreur du modèle se situe sur \(y\) et non sur \(x\). Cela donne l’équation complète de notre modèle statistique :
\[y_i = a \ x_i + b + \epsilon_i\]
avec \(y_i\) est la valeur mesurée pour le point i sur l’axe y, \(a\) est la pente, \(x_i\) est la valeur mesurée pour le point i sur l’axe x, b est l’ordonnée à l’origine et \(\epsilon_i\) les résidus. On peut montrer (nous ne le ferons pas ici pour limiter les développements mathématiques) que le choix des moindres carrés des résidus comme fonction objective revient à considérer que nos résidus suivent une distribution normale centrée autour de zéro et avec un écart type \(\sigma\) constant/ :
\[\epsilon_i \approx N(0, \sigma)\]
Dans le cas de la régression linéaire simple, la meilleure droite s’obtient très facilement par la minimisation de la somme des carrés des résidus. En effet, la pente \(a = \frac{cov_{x, y}}{var_x}\) et l’ordonnée à l’origine \(b = \bar y - a \ \bar x\).
La fonction
lm()permet de faire ce calcul très facilement dans R.
# Régression linéaire
lm. <- lm(data = trees, volume ~ diameter)
# Graphique de nos observations et de la droite obtenue avec la fonction lm()
chart(trees, volume ~ diameter) +
geom_point() +
geom_abline(
aes(intercept = lm.$coefficients[1], slope = lm.$coefficients[2]),
color = "red", size = 1.5) +
labs( color = "Modèle") +
scale_color_viridis_c(direction = -1)
La fonction lm() crée un objet spécifique qui contient de nombreuses informations pour pouvoir ensuite analyser notre modèle linéaire. La fonction class() permet de mettre en avant la classe de notre objet.
class(lm.)# [1] "lm"1.2.4 Résumé avec summary()
Avec la fonction summary() nous obtenons un résumé condensé des informations les plus utiles pour interpréter notre régression linéaire.
summary(lm.)#
# Call:
# lm(formula = volume ~ diameter, data = trees)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.231211 -0.087021 0.003533 0.100594 0.271725
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -1.04748 0.09553 -10.96 7.85e-12 ***
# diameter 5.65154 0.27649 20.44 < 2e-16 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.1206 on 29 degrees of freedom
# Multiple R-squared: 0.9351, Adjusted R-squared: 0.9329
# F-statistic: 417.8 on 1 and 29 DF, p-value: < 2.2e-16- Call :
Il s’agit de la formule employée dans la fonction lm(). C’est à dire le volume en fonction du diamètre du jeu de données trees.
- Residuals :
La tableau nous fournit un résumé via les 5 nombres de l’ensemble des résidus (que vous pouvez récupérer à partir de lm.$residuals).
fivenum(lm.$residuals)# 20 7 12 9 31
# -0.231210947 -0.087020695 0.003532709 0.100594122 0.271724973- Coefficients :
Il s’agit des résultats associés à la pente et à l’ordonnée à l’origine dont les valeurs estimées des paramètres (Estimate). Les mêmes valeurs peuvent être obtenues à partir de lm.$coefficients :
lm.$coefficients# (Intercept) diameter
# -1.047478 5.651535On retrouve également les écart-types calculés sur ces valeurs (Std.Error) qui donnent une indication de la précision de leur estimation, les valeurs des distibutions de Student sur les valeurs estimées (t value) et enfin les valeurs p (PR(>|t|)) liées à un test de Student pour déterminer si le paramètre p correspondant est significativement différent de zéro (avec \(H_0: p = 0\) et \(H_a: p \neq 0\)).
Pour l’instant, nous nous contenterons d’interpréter et d’utiliser les informations issues de summary() dans sa partie supérieure. Le contenu des trois dernières lignes sera détaillé dans le module suivant.
A partir des données de ce résumé, nous pouvons maintenant paramétrer l’équation de notre modèle :
\[y = ax + b\]
devient3 :
\[volume \ de \ bois = 5.65 \ diamètre \ à \ 1.4 \ m - 1.05 \]
Utiliser le carré des résidus a aussi d’autres propriétés statistiques intéressantes qui rapprochent ce calcul de la variance (qui vaut la somme de la distance au carré à la moyenne pour une seule variables numérique).↩
Lors de la paramétrisation du modèle, pensez à arrondir la valeur des paramètres à un nombre de chiffres significatifs raisonnables. Inutile de garder 5, ou même 3 chiffres derrière la virgule si vous n’avez que quelques dizaines d’obserrvations pour ajuster votre modèle.↩