3.5 Modèle linéaire généralisé
Le modèle linéaire nous a permis de combiner différent types de variables indépendantes ou explicatives dans un même modèle. Cependant la variable dépendante ou réponse à la gauche de l’équation doit absolument être numérique et une distribution normale est exigée pour la composante statistique du modèle exprimée dans les résidus \(\epsilon\). Donc, si nous voulons modéliser une variable dépendante qui ne répond pas à ces caractéristiques, nous sommes dans l’impasse avec la fonction lm(). Dans certains cas, une transformation des données peut résoudre le problème. Par exemple, prendre le logarithme d’une variable qui a une distribution log-normale. Dans d’autres cas, il semble qu’il n’y ait pas de solution… C’est ici que la modèle linéaire généralisé vient nous sauver la mise.
Le modèle linéaire généralisé se représente comme suit :
\[ f(y) = \beta_1 + \beta_2 I_2 + \beta_3 I_3 + ... + \beta_k I_k + \beta_l x_1 + \beta_m x_2 + ... + \epsilon \]
La différence par rapport au modèle linéaire, c’est que notre variable dépendante \(y\) est transformée à l’aide d’une fonction \(f(y)\) que l’on appelle fonction de lien. Cette fonction de lien est choisie soigneusement pour transformer une variable qui a une distribution non-normale vers une distribution normale ou quasi-normale. Du coup, il ne faut rien changer à la droite du signe égal par rapport au modèle linéaire, et les outils existants peuvent être réemployés.
Toute la difficulté ici tient donc à la définition des fonctions de liens pertinentes par rapport à la distribution de \(y\). Le tableau suivant reprend les principales situations prises en compte par la fonction glm() dans R qui calcule le modèle linéaire généralisé.
| Distribution de Y | Fonction de lien | Code R |
|---|---|---|
| Gaussienne (Normale) | identité (pas de transfo.) | glm(..., family = gaussian(link = "identity")) |
| Log-Normale | log | glm(..., family = gaussian(link = "log")) |
| Binomiale | logit | glm(..., family = binomial(link = logit)) |
| Binomiale | probit (alternative) | glm(..., family = binomial(link = probit)) |
| Poisson | log | glm(..., family = poisson(link = log)) |
Il en existe bien d’autres. Voyez l’aide de ?family pour plus de détails. Par exemple, pour une variable réponse binaire acceptant seulement deux valeurs possibles et ayant une distribution binomiale, avec une réponse de type logistique (une variation croissante d’une ou plusieurs variables indépendantes fait passer la proportion des individus appartenant au second état selon une courbe logistique en S), une fonction de type logit est à utiliser.
\[ y = 1/(1 + e^{- \beta x}) \]
La transformation logit calcule alors : \(\ln(y / (1 - y)) = \beta x\). Les situations correspondant à ce cas de figure concernent par exemple des variables de type (vivant versus mort) par rapport à une situation potentiellement léthale, ou alors, le développement d’une maladie lors d’une épidémie (sain versus malade).
3.5.1 Exemple
Continuons à analyser nos données concernant les bébés à la naissance. Un bébé prématuré est un bébé qui nait avant 37 semaines de grossesse. Dans notre jeu de données Babies, nous pouvons déterminer si un enfant est prématuré ou non (variable binaire) à partir de la variable gestation(en jours). Transformons nos données pour obtenir les variables d’intérêt.
SciViews::R
babies <- read("babies", package = "UsingR")
babies %>.% select(., gestation, smoke, wt1, ht, race, age) %>.%
# Eliminer les valeurs manquantes
filter(., gestation < 999, smoke < 9, wt1 < 999, ht < 999, race < 99, age < 99) %>.%
# Transformer wt1 en kg et ht en cm
mutate(., wt1 = wt1 * 0.4536) %>.%
mutate(., ht = ht / 39.37) %>.%
# Transformer smoke en variable facteur
mutate(., smoke = as.factor(smoke)) %>.%
# Idem pour race
mutate(., race = as.factor(race)) %>.%
# Déterminer si un bébé est prématuré ou non (en variable facteur)
mutate(., premat = as.factor(as.numeric(gestation < 7*37))) %>.%
# Calculer le BMI comme meilleur index d'embonpoint des mères que leur masse
mutate(., bmi = wt1 / ht^2) ->
Babies_premComment se répartissent les enfants entre prématurés et nés à terme ?
table(Babies_prem$premat)#
# 0 1
# 1080 96Nous avons un nombre relativement faible de prématurés dans l’ensemble. C’était à prévoir. Attention à un plan très mal balancé ici : c’est défavorable à une bonne analyse, mais pas rédhibitoire. Décrivons ces données.
Babies_table <- table(Babies_prem$premat, Babies_prem$smoke)
knitr::kable(addmargins(Babies_table))| 0 | 1 | 2 | 3 | Sum | |
|---|---|---|---|---|---|
| 0 | 486 | 420 | 83 | 91 | 1080 |
| 1 | 39 | 40 | 9 | 8 | 96 |
| Sum | 525 | 460 | 92 | 99 | 1176 |
Ce tableau de contingence ne nous donne pas encore l’idée de la répartition de prématurés en fonction de statut de fumeuse de la mère, mais le graphique suivant nous le montre.
chart(data = Babies_prem, ~smoke %fill=% premat) +
geom_bar(position = "fill")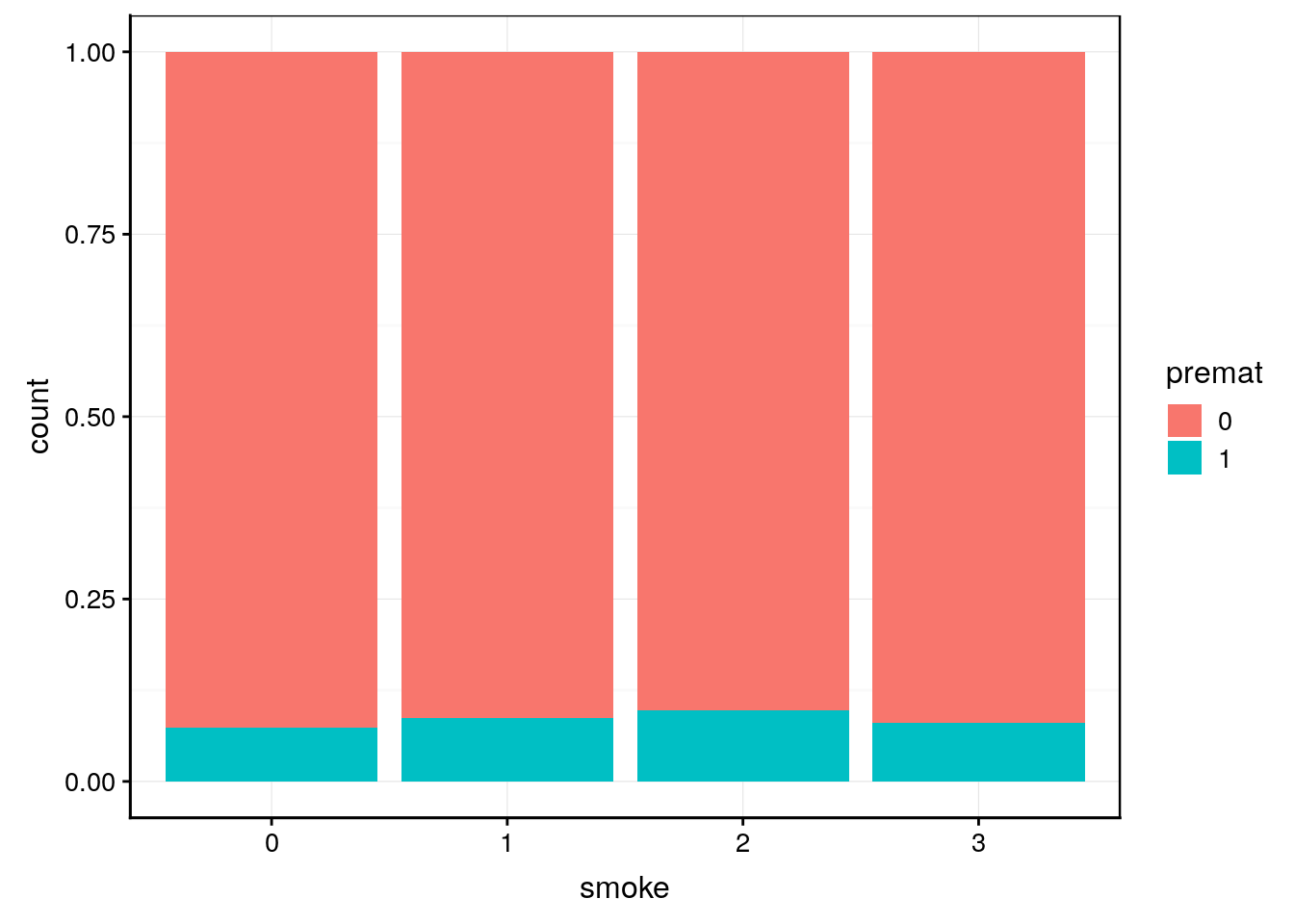
Il ne semble pas y avoir un effet flagrant, même si le niveau smoke == 2 semble contenir une plus forte proportion de prématurés. Qu’en est-il en fonction de l’éthnicité (voir help(babies, packahge = "UsingR") pour le détail sur les variétés éthniques considérées) de la mère (variable race) ?
Babies_table <- table(Babies_prem$premat, Babies_prem$race)
knitr::kable(addmargins(Babies_table))| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Sum | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 491 | 42 | 22 | 58 | 50 | 124 | 31 | 192 | 34 | 24 | 12 | 1080 |
| 1 | 24 | 2 | 5 | 1 | 6 | 8 | 3 | 41 | 5 | 1 | 0 | 96 |
| Sum | 515 | 44 | 27 | 59 | 56 | 132 | 34 | 233 | 39 | 25 | 12 | 1176 |
chart(data = Babies_prem, ~race %fill=% premat) +
geom_bar(position = "fill")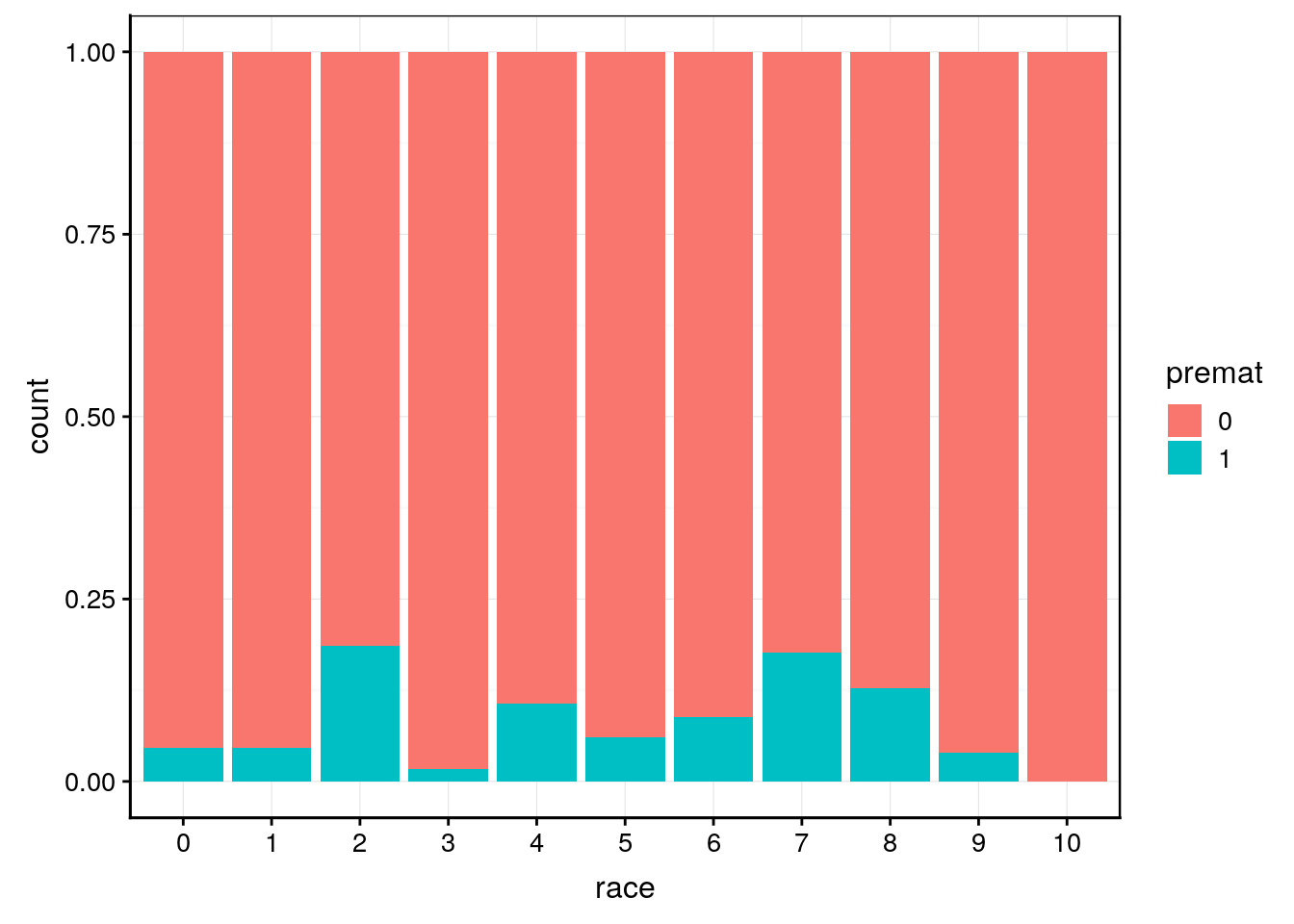
Ici, nous voyons déjà un effet semble-t-il plus marqué. Qu’en est-il du BMI ?
chart(data = Babies_prem, bmi ~ premat) +
geom_boxplot() +
ylab("BMI de la mère")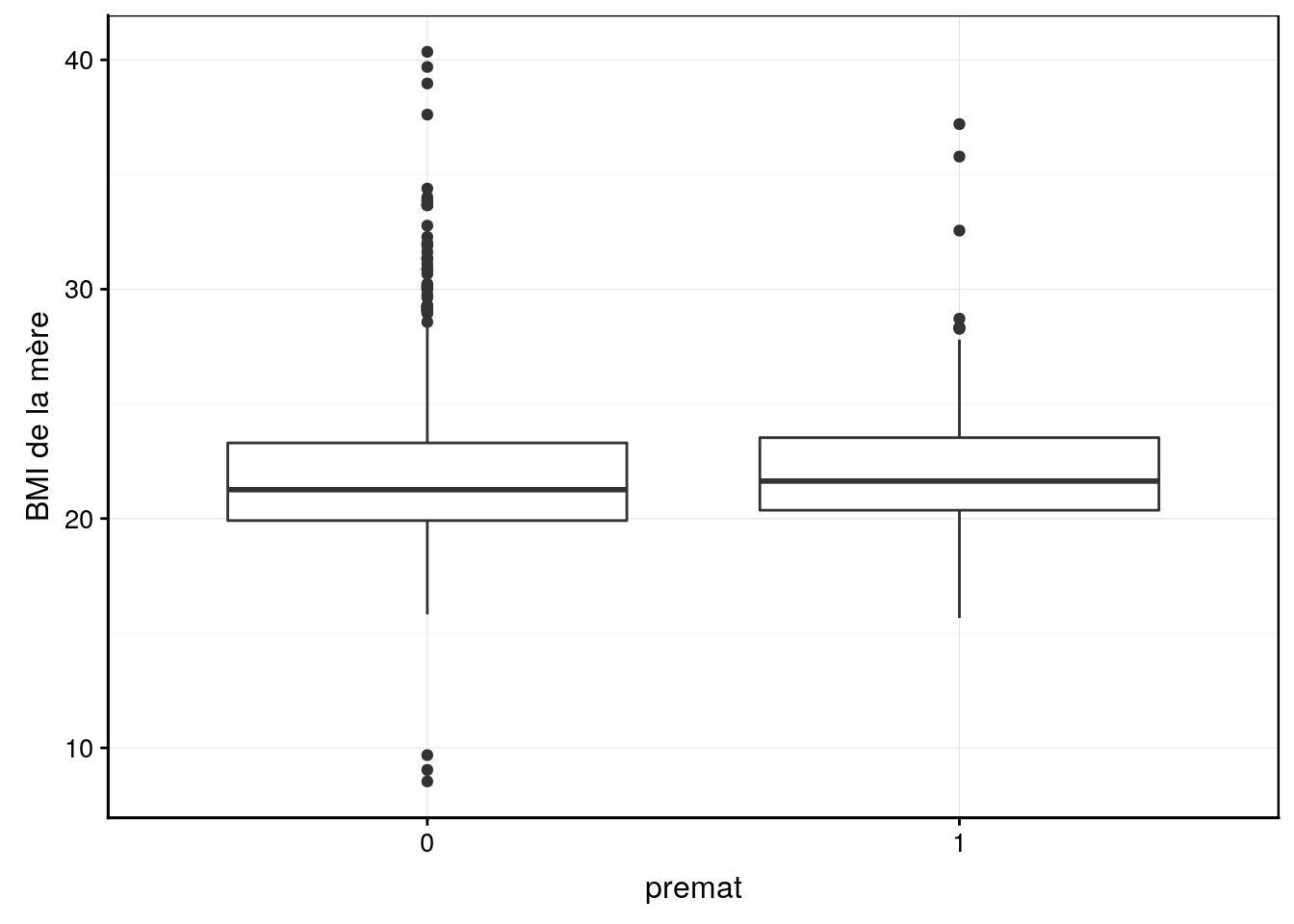
Sur ce graphique, il ne semble pas y avoir d’influence du BMI sur le fait d’avoir un enfant prématuré ou non. Enfin, l’âge de la mère influence-t-il également ?
chart(data = Babies_prem, age ~ premat) +
geom_boxplot() +
ylab("Age de la mère (an)")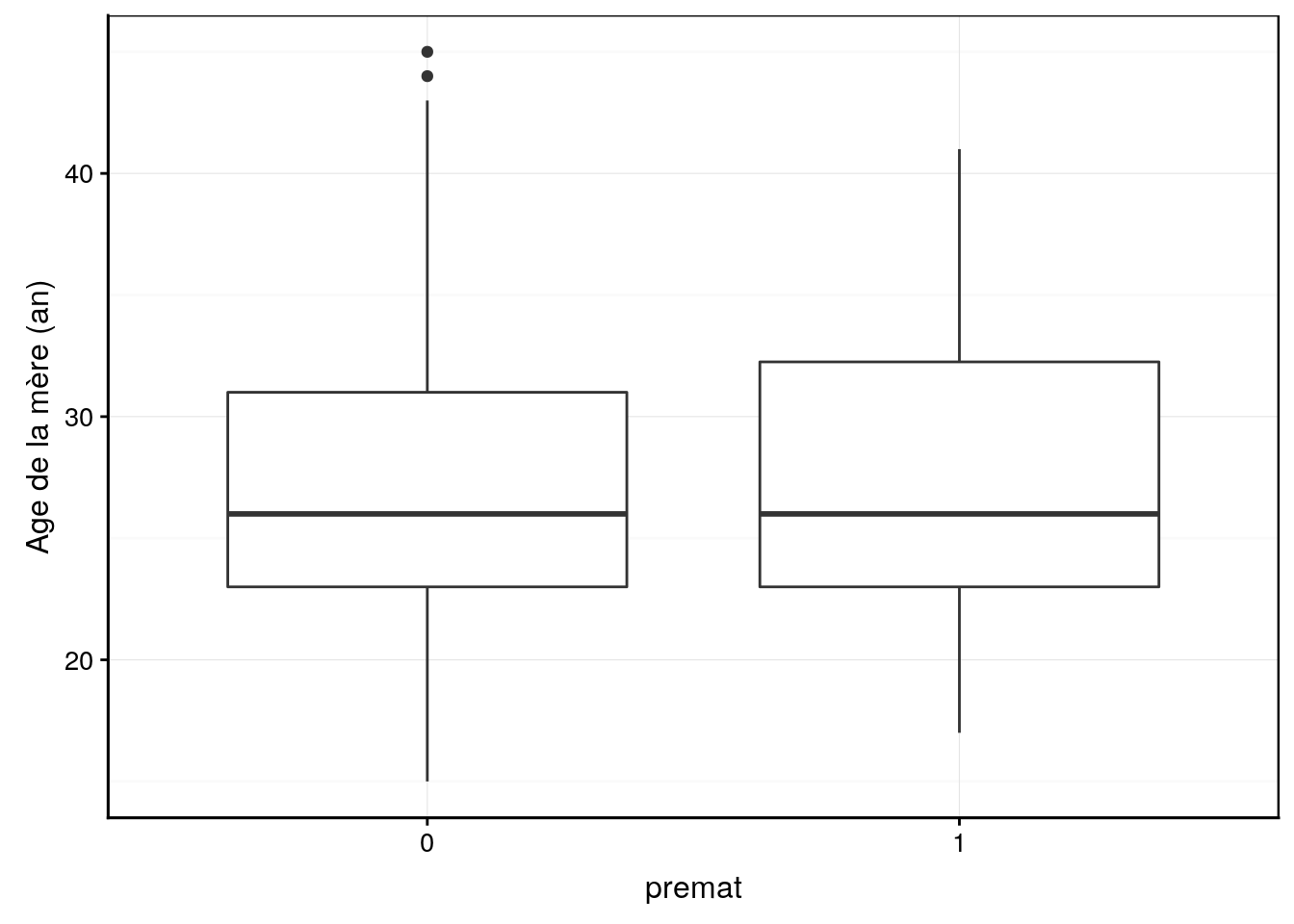
Il ne sembnle pas y avoir un effet flagrant. Voyons ce que donne le modèle (nous ne considérons pas les interactions possibles ici, mais cela doit être fait dans le cas de plusieurs effets significatifs au moins). Avec 4 variables explicatives, le modèle est déjà très complexe sans interactions. Nous serions trop ambitieux de vouloir ici ajuster un modèle complet !
# Modèle linéaire généralisé avec fonction de lien de type logit
Babies_glm <- glm(data = Babies_prem, premat ~ smoke + race + bmi + age,
family = binomial(link = logit))
summary(Babies_glm)#
# Call:
# glm(formula = premat ~ smoke + race + bmi + age, family = binomial(link = logit),
# data = Babies_prem)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -0.6875 -0.4559 -0.3228 -0.2857 2.8199
#
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -3.349082 0.860945 -3.890 0.00010 ***
# smoke1 0.247161 0.244442 1.011 0.31196
# smoke2 0.247474 0.401007 0.617 0.53715
# smoke3 0.245883 0.417970 0.588 0.55634
# race1 -0.037501 0.754621 -0.050 0.96037
# race2 1.510254 0.539895 2.797 0.00515 **
# race3 -1.017780 1.030541 -0.988 0.32334
# race4 0.891191 0.481411 1.851 0.06414 .
# race5 0.303990 0.421363 0.721 0.47064
# race6 0.750868 0.644376 1.165 0.24391
# race7 1.495166 0.280313 5.334 9.61e-08 ***
# race8 1.155898 0.531592 2.174 0.02967 *
# race9 -0.123997 1.043118 -0.119 0.90538
# race10 -13.513140 691.812473 -0.020 0.98442
# bmi -0.001689 0.032621 -0.052 0.95871
# age 0.007806 0.019119 0.408 0.68307
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 665.00 on 1175 degrees of freedom
# Residual deviance: 618.84 on 1160 degrees of freedom
# AIC: 650.84
#
# Number of Fisher Scoring iterations: 15Nous voyons que le résumé de l’objet glm est très similaire à celui d’un objet lm, notamment avec un tableau des Coefficients identique et qui s’interprète de la même manière. Ici, nous pouvons confirmer que ni le fait de fumer, ni l’âge, ni le BMI de la mère n’a d’incidence sur les bébés prématurés au seuil alpha de 5%. En revanche, certaines éthnies sont significativement plus susceptibles d’accoucher avant terme. Cela suggère soit un facteur génétique, soit un facteur environnmental/culturel lié à ces éthnies. Naturellement, il faudrait ici simplifier le modèle qui se ramène en fin de compte à l’équivalent d’une ANOVA à un facteur, mais en version glm() une fois que les variables non significatives sont éliminées. De même, on pourrait légitimement se demander si la variable premat ne pourrait pas aussi être modélisée avec une autre fonction de lien en considérant une distribution de Poisson par exemple. A vous de voir…
A vous de jouer !
- Réalisez un rapport scientifique sur la maturation d’ovocytes, en définissant un modèle linéaire généralisé le plus pertinent pour ces données.
Vous avez à votre disposition une assignation GitHub Classroom.
Pour l’année académique 2019-2020, les URLs à utiliser pour accéder à votre tâche sont les suivants :
Cours de Sciences des données II à Mons : https://classroom.github.com/a/mXAIu4Ir
Pour les autres utilisateurs de ce livre, veuillez faire un “fork” du dépôt ovocytes. Si vous souhaitez accéder à une version précédente particulière de l’exercice, sélectionnez la release correspondante à l’année que vous recherchez.
Lisez le README afin de prendre connaissance de l’exercice.
- Réalisez un rapport scientifique sur la biométrie humaine
Vous avez à votre disposition une assignation GitHub Classroom.
Pour l’année académique 2019-2020, les URLs à utiliser pour accéder à votre tâche sont les suivants :
Cours de Sciences des données II à Mons : https://classroom.github.com/a/hS069etL
Pour les autres utilisateurs de ce livre, veuillez faire un “fork” du dépôt human. Si vous souhaitez accéder à une version précédente particulière de l’exercice, sélectionnez la release correspondante à l’année que vous recherchez.
Lisez le README afin de prendre connaissance de l’exercice.