7.2 Analyse factorielle des correspondances
Comme l’ACP s’intéresse à des corrélations linéaires entre variables quantitatives, elle n’est absolument pas utilisable pour traiter des variables qualitatives. L’Analyse Factorielle des Correspondances sera utile dans ce dernier cas (AFC, ou en anglais “Correspondence Analysis” ou CA).
7.2.1 AFC dans SciViews::R
L’AFC utilises la fonction ca() du package ca dans SciViews::R, mais au stade actuel, tout le code nécessaire (en particulier pour réaliser les graphiques avec chart()) n’est pas encore complètement intégré dans les packages. Ainsi, vous pouvez copier-coller le code du chunk suivant au début de vos scripts ou dans un chunk de setup dans vos documents R Markdown/Notebook.
SciViews::R()
library(broom)
# Au lieu de MASS::corresp(, nf = 2), nous préférons ca::ca()
ca <- ca::ca
scale_axes <- function(data, aspect.ratio = 1) {
range_x <- range(data[, 1])
span_x <- abs(max(range_x) - min(range_x))
range_y <- range(data[, 2])
span_y <- abs(max(range_y) - min(range_y))
if ((span_y / aspect.ratio) > span_x) {
# Adjust range_x
span_x_2 <- span_y / aspect.ratio / 2
range_x_mid <- sum(range_x) / 2
range_x <- c(range_x_mid - span_x_2, range_x_mid + span_x_2)
} else {
# Adjust range_y
span_y_2 <- span_x * aspect.ratio / 2
range_y_mid <- sum(range_y) / 2
range_y <- c(range_y_mid - span_y_2, range_y_mid + span_y_2)
}
list(x = range_x, y = range_y)
}
plot3d <- rgl::plot3d
plot3d.ca <- ca:::plot3d.ca
autoplot.ca <- function(object, choices = 1L:2L,
type = c("screeplot", "altscreeplot", "biplot"), col = "black", fill = "gray",
aspect.ratio = 1, repel = FALSE, ...) {
type = match.arg(type)
res <- switch(type,
screeplot = object %>.% # Classical screeplot
`[[`(., "sv") %>.%
tibble(Dimension = 1:length(.), sv = .) %>.%
chart(data = ., sv^2 ~ Dimension) +
geom_col(col = col, fill = fill) +
labs(y = "Inertia"),
altscreeplot = object %>.% # screeplot represented by dots and lines
`[[`(., "sv") %>.%
tibble(Dimension = 1:length(.), sv = .) %>.%
chart(data = ., sv^2 ~ Dimension) +
geom_line(col = col) +
geom_point(col = "white", fill = col, size = 2, shape = 21, stroke = 3) +
labs(y = "Inertia"),
biplot = {
# We want to use the function plot.ca(), but without plotting the base plot
# So, we place it in a specific environment where all base plot functions are
# fake and do nothing (we just want to collect points coordinates at the end)
env <- new.env()
env$plot_ca <- ca:::plot.ca
environment(env$plot_ca) <- env
env$plot <- function(...) NULL
env$box <- function(...) NULL
env$abline <- function(...) NULL
env$axis <- function(...) NULL
env$par <- function(...) NULL
env$points <- function(...) NULL
env$lines <- function(...) NULL
env$.arrows <- function(...) NULL
env$text <- function(...) NULL
env$strwidth <- function(...) NULL
env$strheight <- function(...) NULL
contribs <- paste0("Dimension ", 1:length(object$sv), " (",
round(object$sv^2 / sum(object$sv^2) * 100, 1), "%)")[choices]
res <- env$plot_ca(object, dim = choices, ...)
rows <- as.data.frame(res$rows)
rows$Type <- "rows"
rows$Labels <- object$rownames
cols <- as.data.frame(res$cols)
cols$Type <- "cols"
cols$Labels <- object$colnames
res <- bind_rows(rows, cols)
names(res) <- c("x", "y", "type", "labels")
lims <- scale_axes(res, aspect.ratio = aspect.ratio)
nudge <- (lims$x[2] - lims$x[1]) / 100
res <- chart(data = res, y ~ x %col=% type %label=% labels) +
geom_hline(yintercept = 0, col = "gray") +
geom_vline(xintercept = 0, col = "gray") +
coord_fixed(ratio = 1, xlim = lims$x, ylim = lims$y, expand = TRUE) +
theme(legend.position = "none") +
labs(x = contribs[1], y = contribs[2])
if (isTRUE(repel)) {
res <- res + geom_point() + ggrepel::geom_text_repel()
} else {# Use text
res <- res + geom_point() +
geom_text(hjust = 0, vjust = 0, nudge_x = nudge, nudge_y = nudge)
}
res
}
)
res
}
chart.ca <- function(data, choices = 1L:2L, ...,
type = c("screeplot", "altscreeplot", "boiplot"), env = parent.frame())
autoplot.ca(data, choices = choices, ..., type = type, env = env)
class(chart.ca) <- c("function", "subsettable_type")7.2.2 Enquête sur la science
L’idée de départ de l’AFC est de pouvoir travailler sur des données qualitatives en les transformant en variables quantitatives via une astuce de calcul, et ensuite de réaliser une ACP sur ce tableau quantitatif pour en représenter l’information visuellement sur une carte. Les enquêtes (mais pas seulement) génèrent souvent des quantités importantes de variables qualitatives qu’il faut ensuite analyser. En effet, des sondage proposent la plupart du temps d’évaluer une question sur une échelle de plusieurs niveaux du genre “tout-à-fait d’accord”, “d’accord”, “pas d’accord”, “pas du tout d’accord”, ce qui donnerait une variable facteur à quatre niveaux ordonnés.
Une grande enquête mondiale a été réalisée en 1993 pour déterminer (entre autre) ce que la population pense de la science en général. Quatre questions sont posées (section 4 de ce questionnaire, voir aussi ici) :
A. Les gens croient trop souvent à la science, et pas assez aux sentiments et à la foi
B. En général, la science moderne fait plus de mal que de bien
C. Tout changement dans la nature apporté par les êtres humains risque d’empirer les choses
D. La science moderne va résoudre nos problèmes relatifs à l’environement sans faire de grands changements à notre mode de vie
Les réponses possibles sont : 1 = tout-à-fait d’accord à 5 = pas du tout d’accord. Le jeu de données wg93 du package ca reprend les réponses données par les allemands de l’ouest à ces questions. De plus, les caractéristiques suivantes des répondants sont enregistrées :
- le sexe (1 = homme, 2 = femme),
- l’âge (1 = 18-24, 2 = 25-34, 3 = 35-44, 4 = 45-54, 5 = 55-64, 6 = 65+)
- le niveau d’éducation (1 = primaire, 2 = second. partim, 3 = secondaire, 4 = univ. partim, 5 = univ. cycle 1, 6 = univ. cycle 2+)
wg <- read("wg93", package = "ca")
wg# # A tibble: 871 x 7
# A B C D sex age edu
# <fct> <fct> <fct> <fct> <fct> <fct> <fct>
# 1 2 3 4 3 2 2 3
# 2 3 4 2 3 1 3 4
# 3 2 3 2 4 2 3 2
# 4 2 2 2 2 1 2 3
# 5 3 3 3 3 1 5 2
# 6 3 4 4 5 1 3 2
# 7 3 4 2 4 2 5 2
# 8 3 4 4 2 1 3 3
# 9 3 2 2 1 1 3 2
# 10 3 3 2 2 1 3 2
# # … with 861 more rowsCeci est un tableau cas par variables avec sept variables facteurs et 871 cas. Nous commençons par réencoder les niveaux des variables pour plus de clarté :
wg %>.%
mutate(.,
A = recode(A, `1` = "++", `2` = "+", `3` = "0", `4` = "-", `5` = "--"),
B = recode(B, `1` = "++", `2` = "+", `3` = "0", `4` = "-", `5` = "--"),
C = recode(C, `1` = "++", `2` = "+", `3` = "0", `4` = "-", `5` = "--"),
D = recode(D, `1` = "++", `2` = "+", `3` = "0", `4` = "-", `5` = "--"),
sex = recode(sex, `1` = "H", `2`= "F"),
age = recode(age, `1` = "18-24", `2` = "25-34", `3` = "35-44",
`4` = "45-54", `5` = "55-64", `6` = "65+"),
edu = recode(edu, `1` = "primaire", `2` = "sec. part", `3` = "secondaire",
`4` = "univ. part", `5` = "univ. cycle 1", `6` = "univ. cycle 2")
) -> wg
wg# # A tibble: 871 x 7
# A B C D sex age edu
# <fct> <fct> <fct> <fct> <fct> <fct> <fct>
# 1 + 0 - 0 F 25-34 secondaire
# 2 0 - + 0 H 35-44 univ. part
# 3 + 0 + - F 35-44 sec. part
# 4 + + + + H 25-34 secondaire
# 5 0 0 0 0 H 55-64 sec. part
# 6 0 - - -- H 35-44 sec. part
# 7 0 - + - F 55-64 sec. part
# 8 0 - - + H 35-44 secondaire
# 9 0 + + ++ H 35-44 sec. part
# 10 0 0 + + H 35-44 sec. part
# # … with 861 more rowsPar exemple, si nous nous posons la question de l’impact de l’éducation sur l’impression que la science est néfaste (question B), nous pourrons faire l’analyse suivante :
- Étape 1 : calcul du tableau de contingence à double entrée croisant les réponses à la question B avec le niveau d’éducation des répondants :
table(wg$B, wg$edu)#
# primaire sec. part secondaire univ. part univ. cycle 1 univ. cycle 2
# ++ 6 34 19 6 4 2
# + 10 93 47 12 5 7
# 0 11 95 55 18 11 15
# - 7 112 82 37 16 27
# -- 4 44 39 21 13 19- Étape 2 : test de Chi2 d’indépendance, voir section 8.2 du cours de SDD I. L’hypothèse nulle du test est quel les deux variables sont indépendantes l’une de l’autre. L’hypothèse alternative est qu’une dépendance existe. Si la réponse aux questions est indépendante du niveau d’éducation (pas de rejet de H0), notre analyse est terminée. Sinon, il faut approfondir… Choisissons notre seuil \(\alpha\) à 5% avant de réaliser notre test.
chisq.test(wg$B, wg$edu)# Warning in chisq.test(wg$B, wg$edu): Chi-squared approximation may be
# incorrect#
# Pearson's Chi-squared test
#
# data: wg$B and wg$edu
# X-squared = 42.764, df = 20, p-value = 0.002196L’avertissement nous prévient qu’une approximation a du être réalisée, mais le test reste utilisable si la valeur est loin du seuil \(/alpha\). La valeur p de 0,2% est très inférieure à \(\alpha\). Nous rejettons H0. Il y a dépendance entre le niveau d’éducation et la réponse à la question B. OK, mais comment se fait cette dépendance ? C’est ici que l’AFC nous vient en aide.
-Étape 3 : Si l’hypothèse nulle est rejettée, il faut analyser plus en profondeur. L’AFC va présenter la dépendance de manière claire. La fonction ca() accepte un jeu de données dans l’argument data = et une formule qui spécifie dans le terme de droite les deux variables à croiser séparées par un signe + (~ fact1 + fact2). Donc :
wg_b_edu <- ca(data = wg, ~ B + edu)
wg_b_edu#
# Principal inertias (eigenvalues):
# 1 2 3 4
# Value 0.043989 0.004191 0.000914 4e-06
# Percentage 89.59% 8.54% 1.86% 0.01%
#
#
# Rows:
# ++ + 0 - --
# Mass 0.081515 0.199770 0.235362 0.322618 0.160735
# ChiDist 0.286891 0.274685 0.095627 0.141176 0.341388
# Inertia 0.006709 0.015073 0.002152 0.006430 0.018733
# Dim. 1 -1.140162 -1.293374 -0.406059 0.591115 1.593838
# Dim. 2 -2.211930 0.641674 -0.409771 0.976000 -1.034695
#
#
# Columns:
# primaire sec. part secondaire univ. part univ. cycle 1
# Mass 0.043628 0.433984 0.277842 0.107922 0.056257
# ChiDist 0.427367 0.164446 0.036882 0.279471 0.341163
# Inertia 0.007968 0.011736 0.000378 0.008429 0.006548
# Dim. 1 -1.722505 -0.773101 0.115183 1.302120 1.428782
# Dim. 2 -3.523982 0.381160 0.336612 0.235984 -2.516238
# univ. cycle 2
# Mass 0.080367
# ChiDist 0.417941
# Inertia 0.014038
# Dim. 1 1.962905
# Dim. 2 0.135512Nous retrouvons les valeurs propres (eigenvalues) qui représentent l’inertie exprimée sur les différents axes, avec le pourcentage juste en dessous. Les deux tableaux suivants détaillent les calculs. Il n’est pas indispensable de comprendre tout ce qui s’y trouve, mais notez que les composantes du calcul du Chi2 pour chaque niveau des variables sont reprises à la ligne ChiDist. Nous y reviendrons. La méthode summary() ainsi que le graphique des éboulis via chart$scree() nous donnent une information plus claire sur la contribution de la variabilité totale sur les différents axes. Cela nous aide à décider si le plan réduit aux deux premiers axes que nous utiliserons ensuite est adéquat ou non (pourcentage suffisant = données bien représentées dans ce plan).
summary(wg_b_edu, scree = TRUE, rows = FALSE, columns = FALSE)#
# Principal inertias (eigenvalues):
#
# dim value % cum% scree plot
# 1 0.043989 89.6 89.6 **********************
# 2 0.004191 8.5 98.1 **
# 3 0.000914 1.9 100.0
# 4 4e-06000 0.0 100.0
# -------- -----
# Total: 0.049097 100.0chart$scree(wg_b_edu)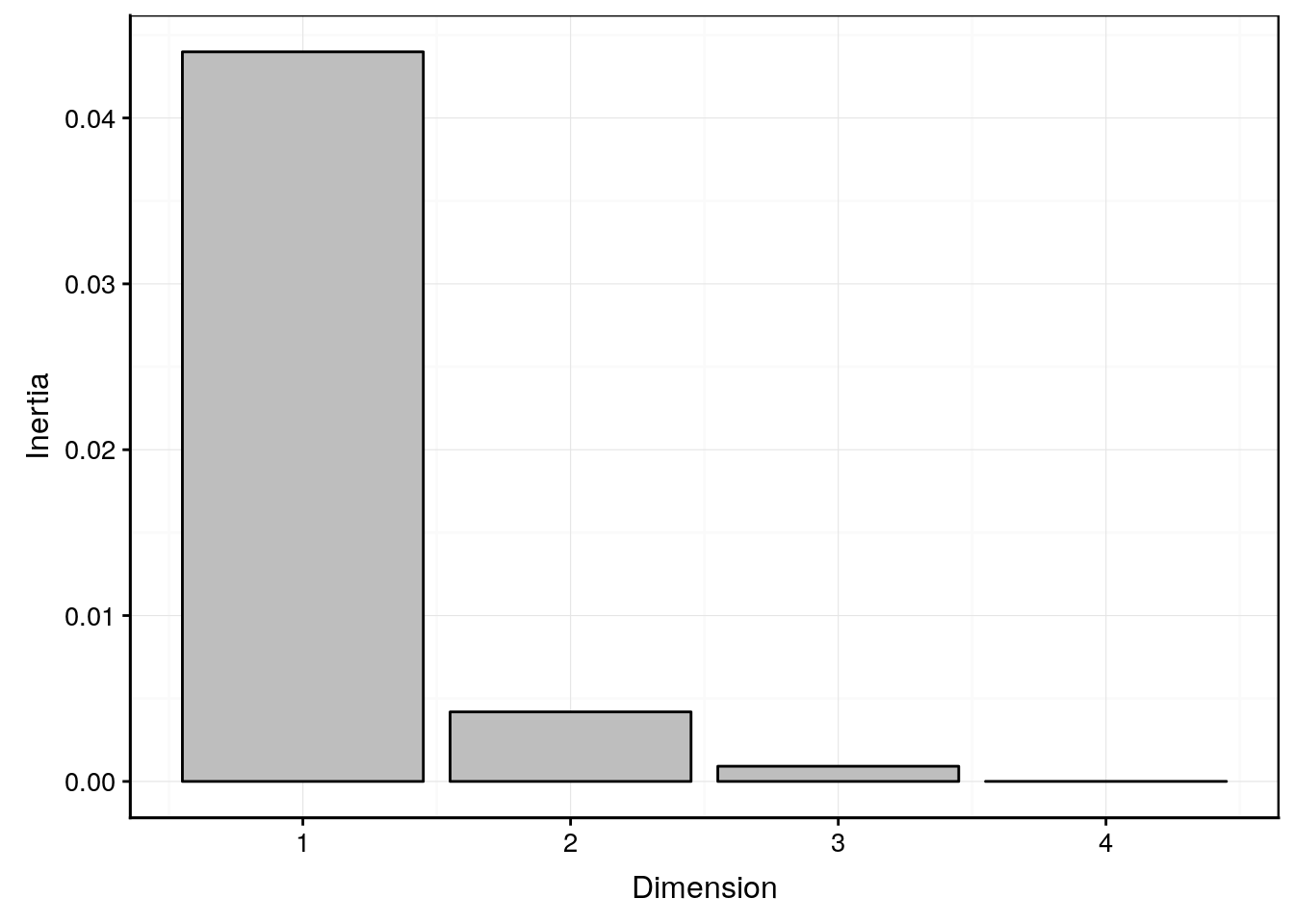
Ici, les deux premiers axes cumulent plus de 98% de la variation totale. Nous pouvons donc continuer en toute confiance. Le biplot va ici projetter les individus sur la carte (les individus étant en fait les différents niveaux des deux variables, obtenus après réalisation de deux ACP, l’une sur les colonnes et l’autre sur les lignes). Les deux groupes sont représentés par des couleurs différentes, mais sur une même carte. C’erst la fonction chart$biplot() qui réalise ce graphique.
chart$biplot(wg_b_edu, choices = c(1, 2))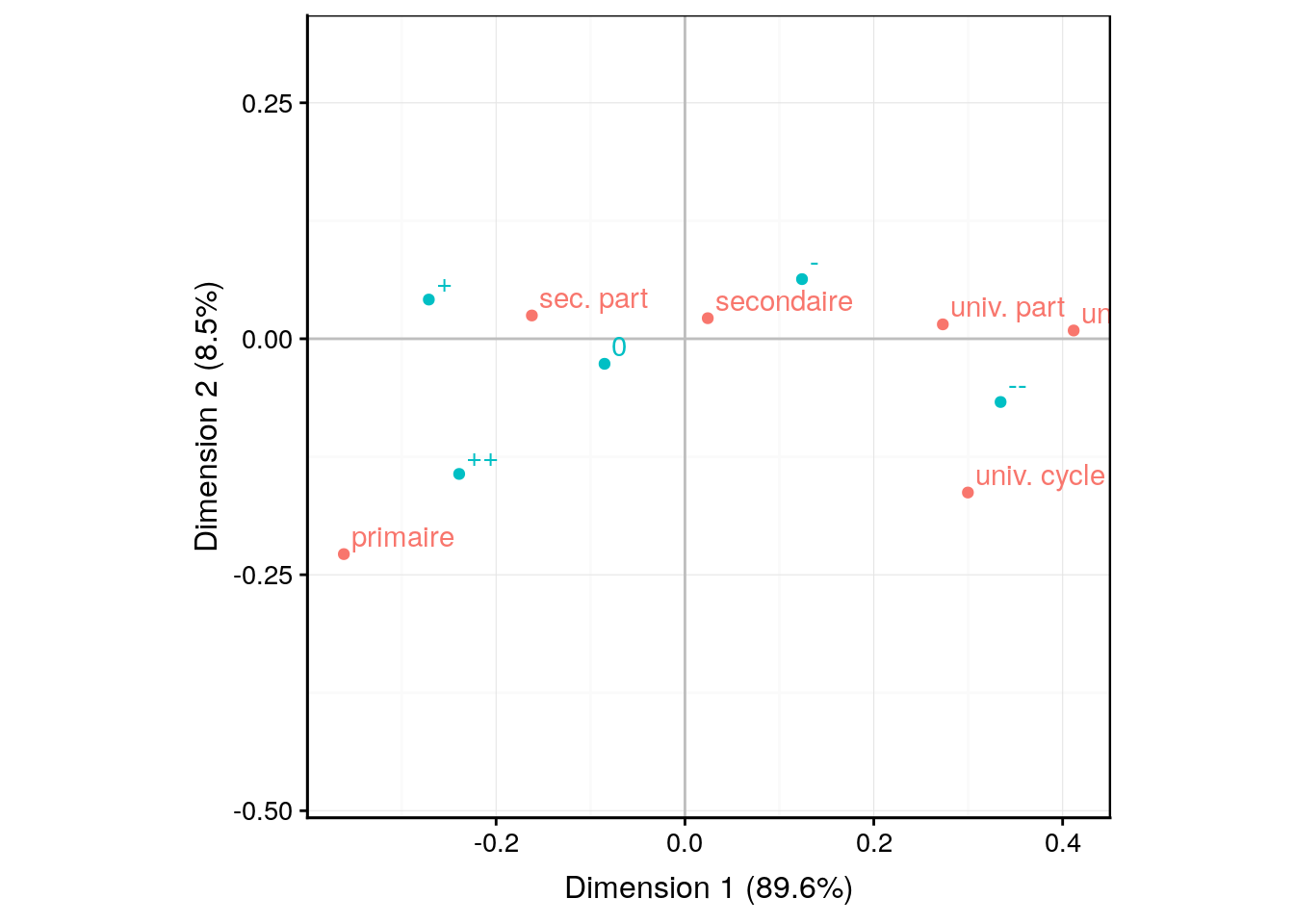
L’interprétation se fait d’abord sur les points d’une couleur (niveau de la première variable), puis sur ceux de l’autre (niveaux de la seconde variable), et enfin, conjointement. Voici ce que cela donne ici :
Les niveaux d’éducation en rouge sont globalement représentés essentiellement de gauche à droite dans un ordre croissant de “études primaires” jusqu’à “études universitaires de 2éme cycle ou plus”.
Les réponses à la question B (en bleu turquoise) sont également rangés globalement de gauche à droite (avec une légère inversion entre
+et++) depuis ceux qui sont tout-à-fait d’accord que la science moderne est néfaste à la gauche jusqu’à ceux qui ne le sont pas du tout à la droite.Conjointement, on va comparer les points rouges et les bleus et regarder ceux qui se situent dans une direction similaire par rapport au centre d’inertie à la coordonnée {0, 0} matérialisée par la croix grise20. Ainsi, nous constatons que ceux qui ont le niveau éducatif le plus faible (niveau primaire) ont globalement plutôt répondu qu’ils sont tout-à-fait d’accord (
++), alors qu’à l’opposé, les universitaires ne sont pas du tous d’accord avec l’affirmation (--).
L’essentiel se lit ici effectivement sur un seul axe (dimension 1) qui capture environ 90% de la variation totale. Le second axe vient moduler légèrement ce classement avec 8,5% de variabilité, mais sans tout bouleverser.
Ici la lecture de la carte générée par l’AFC est limpide… Et manifestement, nous pouvions légitimement conclure à l’époque qu’un effort éducatif et d’information était nécessaire auprès de la population la moins éduquée pour leur faire prendre conscience de l’intérêt de la science moderne (à moins que cette dernière remarque ne soit un parti pris… d’un universtaire :-).
7.2.3 Des acariens sinon rien
Un deuxième exemple illustre une utilisation légèrement différente de l’AFC. Il s’agit des tableaux de type “espèces par stations”. Ces tableaux contiennent différentes espèces ou autres groupes taxonomiques dénombrés dans plusieurs échantillons prélevés à des stations différentes. Le dénombrement des espèces peut être quantitatif (nombre d’individus observés par unité de surface ou de volume), semi-quantitatif (peu, moyen, beaucoup), ou même binaire (présence ou absence de l’espèce). Ces tableaux sont assimilables, en réalité, à des tableaux de contingence à double entrée qui croisent deux variables qualitatives “espèce” et “station”. C’est comme si la première étape avait déjà été réalisée dans l’analyse précédente du jeu de données wg.
Naturellement, comme il ne s’agit pas réellement d’un tableau de contingence, nous ne réaliserons pas le test Chi2 d’indépendance ici, et nous passerons directement à l’étape de l’AFC. L’exemple choisi concerne des populations d’acariens dans de la litière (acarien se dit “mite” en anglais, d’où le nom du jeu de données issu du package vegan).
mite <- read("mite", package = "vegan")
skimr::skim(mite)# Skim summary statistics
# n obs: 70
# n variables: 35
#
# ── Variable type:integer ──────────────────────────────────────────────────────────────────────────────────────────────
# variable missing complete n mean sd p0 p25 p50 p75 p100 hist
# Brachy 0 70 70 8.73 10.08 0 3 4.5 11.75 42 ▇▂▁▂▁▁▁▁
# Ceratoz1 0 70 70 1.29 1.46 0 0 1 2 5 ▇▆▁▃▁▁▁▁
# Ceratoz3 0 70 70 1.3 2.2 0 0 0 2 9 ▇▁▁▁▁▁▁▁
# Eupelops 0 70 70 0.64 0.99 0 0 0 1 4 ▇▃▁▁▁▁▁▁
# FSET 0 70 70 1.86 3.18 0 0 0 2 12 ▇▂▁▁▁▁▁▁
# Galumna1 0 70 70 0.96 1.73 0 0 0 1 8 ▇▁▁▁▁▁▁▁
# HMIN 0 70 70 4.91 8.47 0 0 0 4.75 36 ▇▁▁▁▁▁▁▁
# HMIN2 0 70 70 1.96 3.92 0 0 0 2.75 20 ▇▂▁▁▁▁▁▁
# HPAV 0 70 70 8.51 7.56 0 4 6.5 12 37 ▇▇▃▃▁▁▁▁
# HRUF 0 70 70 0.23 0.62 0 0 0 0 3 ▇▁▁▁▁▁▁▁
# LCIL 0 70 70 35.26 88.85 0 1.25 13 44 723 ▇▁▁▁▁▁▁▁
# Lepidzts 0 70 70 0.17 0.54 0 0 0 0 3 ▇▁▁▁▁▁▁▁
# LRUG 0 70 70 10.43 12.66 0 0 4.5 17.75 57 ▇▂▂▁▁▁▁▁
# MEGR 0 70 70 2.19 3.62 0 0 1 3 17 ▇▂▁▁▁▁▁▁
# Miniglmn 0 70 70 0.24 0.79 0 0 0 0 5 ▇▁▁▁▁▁▁▁
# MPRO 0 70 70 0.16 0.47 0 0 0 0 2 ▇▁▁▁▁▁▁▁
# NCOR 0 70 70 1.13 1.65 0 0 0.5 1.75 7 ▇▃▂▂▁▁▁▁
# NPRA 0 70 70 1.89 2.37 0 0 1 2.75 10 ▇▂▂▁▁▁▁▁
# ONOV 0 70 70 17.27 18.05 0 5 10.5 24.25 73 ▇▃▂▁▁▁▁▁
# Oppiminu 0 70 70 1.11 1.84 0 0 0 1.75 9 ▇▁▁▁▁▁▁▁
# Oribatl1 0 70 70 1.89 3.43 0 0 0 2.75 17 ▇▁▁▁▁▁▁▁
# PHTH 0 70 70 1.27 2.17 0 0 0 2 8 ▇▁▁▁▁▁▁▁
# PLAG2 0 70 70 0.8 1.79 0 0 0 1 9 ▇▁▁▁▁▁▁▁
# PPEL 0 70 70 0.17 0.54 0 0 0 0 3 ▇▁▁▁▁▁▁▁
# Protopl 0 70 70 0.37 1.61 0 0 0 0 13 ▇▁▁▁▁▁▁▁
# PWIL 0 70 70 1.09 1.71 0 0 0 1 8 ▇▁▁▁▁▁▁▁
# RARD 0 70 70 1.21 2.78 0 0 0 1 13 ▇▂▁▁▁▁▁▁
# SLAT 0 70 70 0.4 1.23 0 0 0 0 8 ▇▁▁▁▁▁▁▁
# SSTR 0 70 70 0.31 0.97 0 0 0 0 6 ▇▁▁▁▁▁▁▁
# Stgncrs2 0 70 70 0.73 1.83 0 0 0 0 9 ▇▁▁▁▁▁▁▁
# SUCT 0 70 70 16.96 13.89 0 7.25 13.5 24 63 ▇▇▆▅▂▁▁▁
# Trhypch1 0 70 70 2.61 6.14 0 0 0 2 29 ▇▁▁▁▁▁▁▁
# Trimalc2 0 70 70 2.07 5.79 0 0 0 0 33 ▇▁▁▁▁▁▁▁
# TVEL 0 70 70 9.06 10.93 0 0 3 19 42 ▇▁▁▂▁▁▁▁
# TVIE 0 70 70 0.83 1.47 0 0 0 1 7 ▇▁▁▁▁▁▁▁35 espèces d’acariens sont dénombrés en 70 stations différentes, et il n’y a aucunes valeurs manquantes. Comme il ne peut y avoir aucun total de ligne ou de colonne égal à zéro pour le calcul des Chi2 (sinon, on aurait une division par zéro), nous vérifions cela de la façon suivante :
rowSums(mite)# [1] 140 268 186 286 199 209 162 126 123 166 216 213 177 269 100 97 90
# [18] 118 118 184 117 172 81 80 123 120 173 111 111 96 130 93 136 194
# [35] 111 133 139 189 94 157 81 140 148 60 158 154 121 113 107 148 91
# [52] 112 145 49 58 108 8 121 90 127 42 13 86 88 112 116 781 111
# [69] 184 121colSums(mite)# Brachy PHTH HPAV RARD SSTR Protopl MEGR MPRO
# 611 89 596 85 22 26 153 11
# TVIE HMIN HMIN2 NPRA TVEL ONOV SUCT LCIL
# 58 344 137 132 634 1209 1187 2468
# Oribatl1 Ceratoz1 PWIL Galumna1 Stgncrs2 HRUF Trhypch1 PPEL
# 132 90 76 67 51 16 183 12
# NCOR SLAT FSET Lepidzts Eupelops Miniglmn LRUG PLAG2
# 79 28 130 12 45 17 730 56
# Ceratoz3 Oppiminu Trimalc2
# 91 78 145De plus, l’AFC est très sensible à la présence de valeurs extrêmes. Il faut être particulièrement attentif à ne pas avoir trop de disparité, surtout en présence d’espèces très abondantes versus d’autres très rares. Si quelques échantillons contiennent une quantité particulièrement large d’items, cela peut aussi être problématique. Pour des dénombrements ou du semi-quantitatif à plus d’une dizaine de niveaux, la boite de dispersion parallèle est un bon graphique, mais nous devons tronsformer le tableau de données en format long avec gather() pour pouvoir le faire, et ensuite, nous présentons les espèces sur l’axe des ordonnées avec coord_flip() :
mite %>.%
gather(., key = "species", value = "n") %>.%
chart(., n ~ species) +
geom_boxplot() +
coord_flip()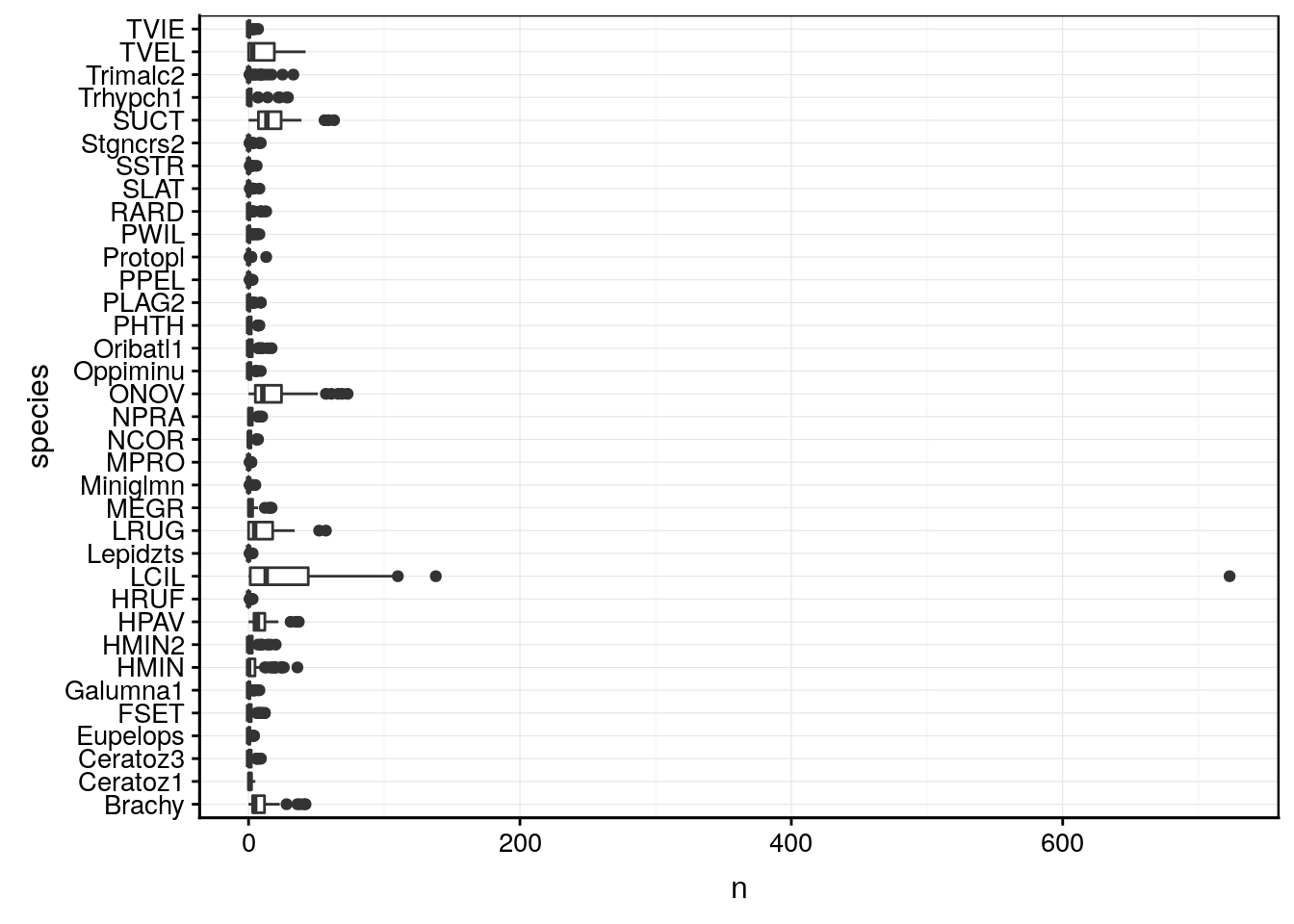
Aïe ! Nous avons ici une magnifique valeur extrême, ainsi que des différences trop nettes entre les espèces les plus abondantes et les plus rares. Nous devons y remédier avant de faire notre AFC. Deux solutions sont possibles :
- Soit nous dégradons l’information vers du semi-quantitatif en définissant des niveaux d’abondance, du genre 0, 1-10, 10-20, 20-30, 31+. Nous pouvons réaliser cela avec la fonction
cut()illustrée ici sur un exemple fictif.
sample <- c(0, 12, 500, 25, 5)
cut(sample, breaks = c(-1, 0, 10, 20, 30, Inf))# [1] (-1,0] (10,20] (30,Inf] (20,30] (0,10]
# Levels: (-1,0] (0,10] (10,20] (20,30] (30,Inf]Nous voyons que cut() a ici remplacé nos données quantitatives dans sample() en une variable qualitative à cinq niveaux clairement libellés. Notez l’astuce du groupe (-1,0] pour capturer les valeurs nulles dans un groupe séparé.
- Autre solution, nous transformons les données pour réduire l’écart entre les extrêmes. Typiquement, une transformation \(log(x + 1)\) est efficace pour cela, et fonctionne bien en présence de valeurs nulles aussi. Nous utiliserons cette dernière technique pour notre jeu de données
mite. Enfin, nous nous assurons que les station sont bien numérotées de 1 à 70 en lignes (rownames()).
mite2 <- log1p(as.data.frame(mite))
# Ajouter le numéro des stations explicitement
rownames(mite2) <- 1:nrow(mite2)Le graphique boite de dispersion parallèle montre plus d’homogénéité maintenant :
mite2 %>.%
gather(., key = "species", value = "log_n_1") %>.%
chart(., log_n_1 ~ species) +
geom_boxplot() + coord_flip()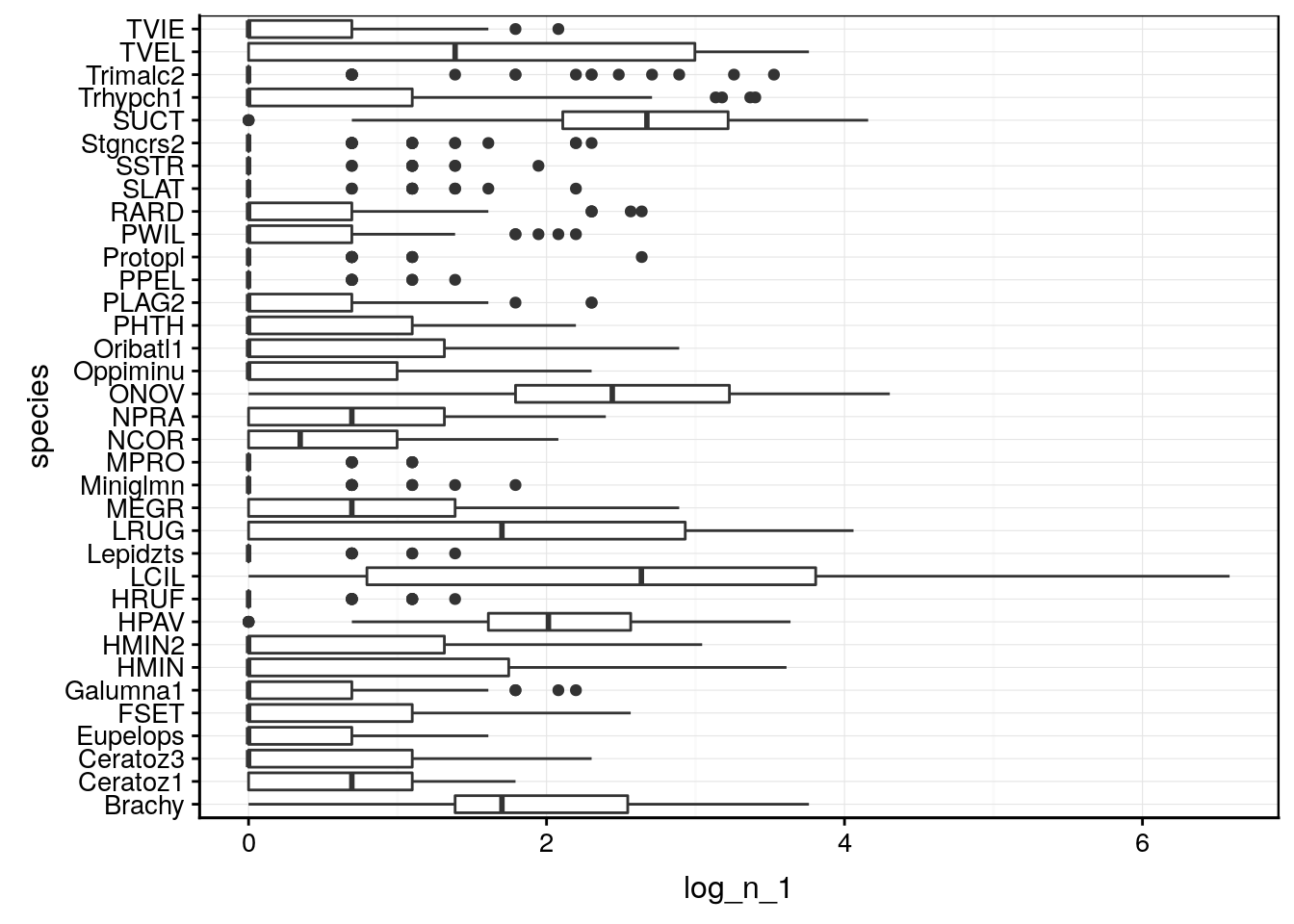
A noter que ce type de graphique ne convient pas pour les données semi-quantitatives ou qualitatives. Nous pouvons réaliser le graphique suivant à la place dans ce cas pour visualiser la distribution des espèces dans les différentes stations (qui fonctionne aussi en quantitatif) :
mite2 %>.%
gather(., key = "species", value = "n") %>.%
mutate(., station = rep(1:nrow(mite), ncol(mite))) %>.%
chart(., species ~ station %fill=% n) +
geom_raster()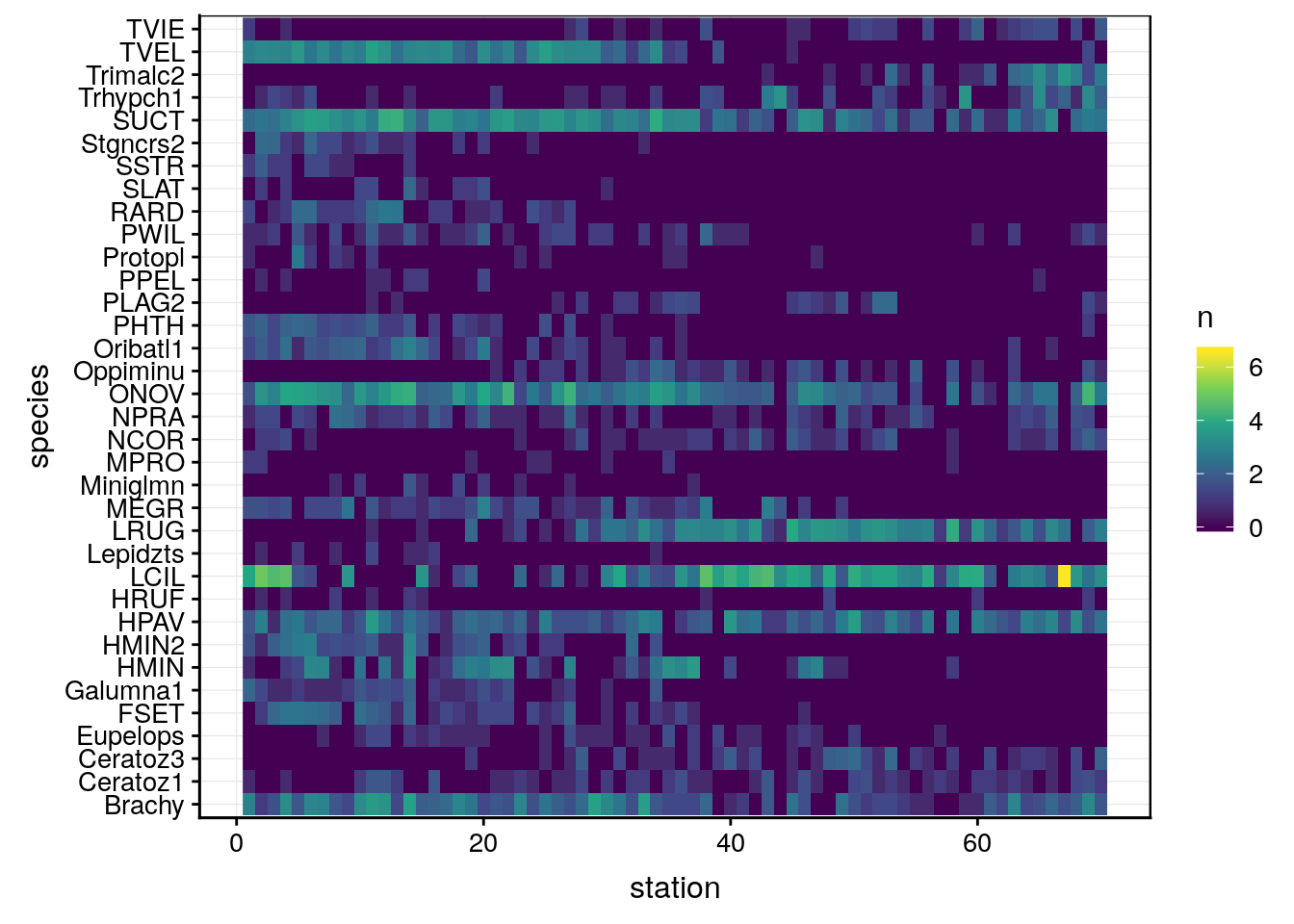
Maintenant que nos données sont vérifiées, nettoyées (phase de préparation), et décrites correctement (phase descriptive), nous pouvons réaliser notre AFC et explorer les particularités de ce jeu de données en vue d’une étude plus approfondie ultérieure (phase exploratoire). L’utilisation de ca() sur un tableau de type contingence à double entrée déjà prêt est ultra-simple. Il suffit de fournir le tableau en question comme seul argument à la fonction.
mite2_ca <- ca(mite2)Examinons la variabilité sur les différents axes, numériquement et à l’aide du graphe des éboulis :
summary(mite2_ca, scree = TRUE, rows = FALSE, columns = FALSE)#
# Principal inertias (eigenvalues):
#
# dim value % cum% scree plot
# 1 0.366209 31.5 31.5 ********
# 2 0.132783 11.4 42.9 ***
# 3 0.072315 6.2 49.1 **
# 4 0.065787 5.7 54.7 *
# 5 0.055872 4.8 59.5 *
# 6 0.048122 4.1 63.7 *
# 7 0.041834 3.6 67.3 *
# 8 0.039072 3.4 70.6 *
# 9 0.032183 2.8 73.4 *
# 10 0.031300 2.7 76.1 *
# 11 0.028809 2.5 78.6 *
# 12 0.026949 2.3 80.9 *
# 13 0.024701 2.1 83.0 *
# 14 0.022729 2.0 84.9
# 15 0.020618 1.8 86.7
# 16 0.018029 1.5 88.3
# 17 0.016836 1.4 89.7
# 18 0.014850 1.3 91.0
# 19 0.014217 1.2 92.2
# 20 0.012553 1.1 93.3
# 21 0.010879 0.9 94.2
# 22 0.010412 0.9 95.1
# 23 0.009703 0.8 96.0
# 24 0.008187 0.7 96.7
# 25 0.007294 0.6 97.3
# 26 0.006689 0.6 97.9
# 27 0.005343 0.5 98.3
# 28 0.004576 0.4 98.7
# 29 0.004020 0.3 99.1
# 30 0.003828 0.3 99.4
# 31 0.002732 0.2 99.6
# 32 0.001955 0.2 99.8
# 33 0.001656 0.1 99.9
# 34 0.000776 0.1 100.0
# -------- -----
# Total: 1.163821 100.0chart$scree(mite2_ca, fill = "cornsilk")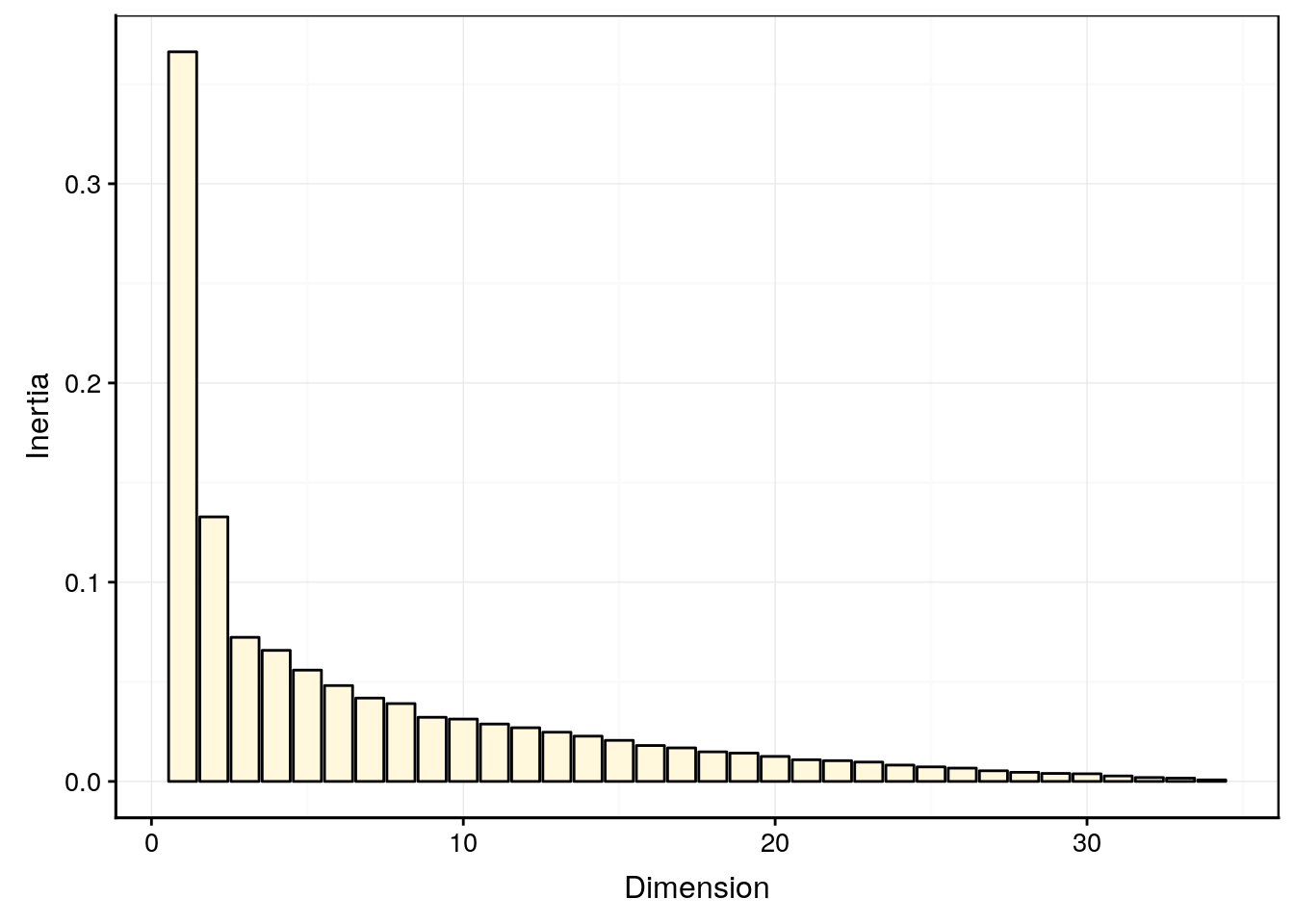
La variabilité décroit rapidement sur les deux premiers axes, et ensuite plus lentement. Les deux premières dimensions ne capturent qu’environ 43% de la variabilité totale. Toutefois, la variation moins brutale par après justifie de ne garder que deux axes. Malgré la représentativité relativement faible dans ce plan, nous verrons que l’AFC reste interprétable et peut fournir des informations utiles, même dans ce cas. Voici la carte (biplot) :
chart$biplot(mite2_ca, choices = c(1, 2))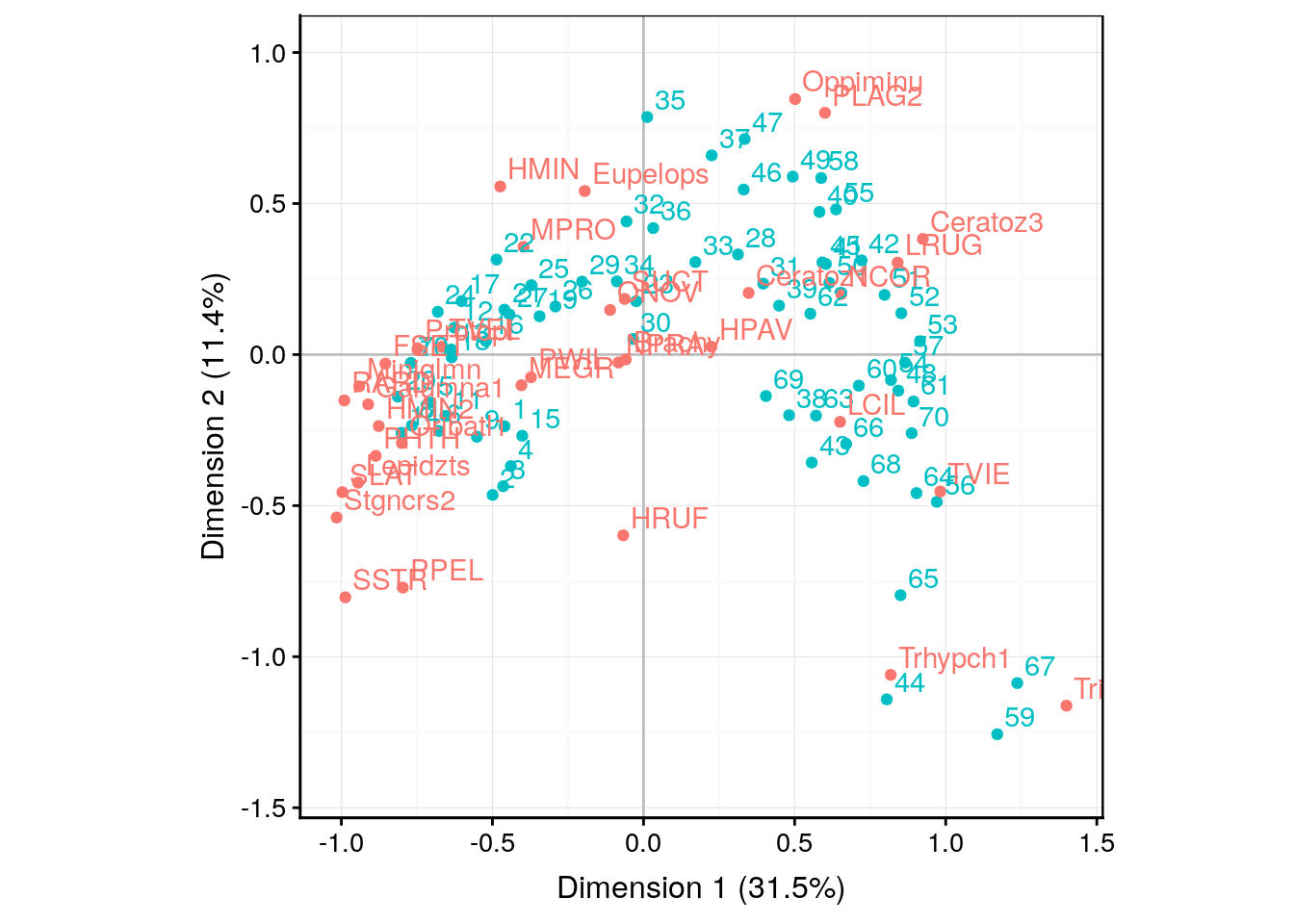
Nous observons une forme en fer à cheval de la distribution des points. Attention ! Ceci est un artéfact lié au fait que la distance du Chi2 a tendance à rapprocher les extrêmes (“qui se ressemblent dans la différence”, en quelque sorte) alors que notre souhait aurait plutôt été de les placer aux extrémités du graphique. Il faut donc analyser les données comme une transition progressive d’un état A vers un état B le long de la forme en fer à cheval.
Lorsqu’il y a beaucoup de points, ce graphique tend à être très encombré et illisible. L’argument repel = TRUE vient parfois aider en allant placer les labels de telle façon qu’ils se chevauchent le moins possible. Par contre, la forme du nuage de point est du coup un peu moins visible.
chart$biplot(mite2_ca, choices = c(1, 2), repel = TRUE)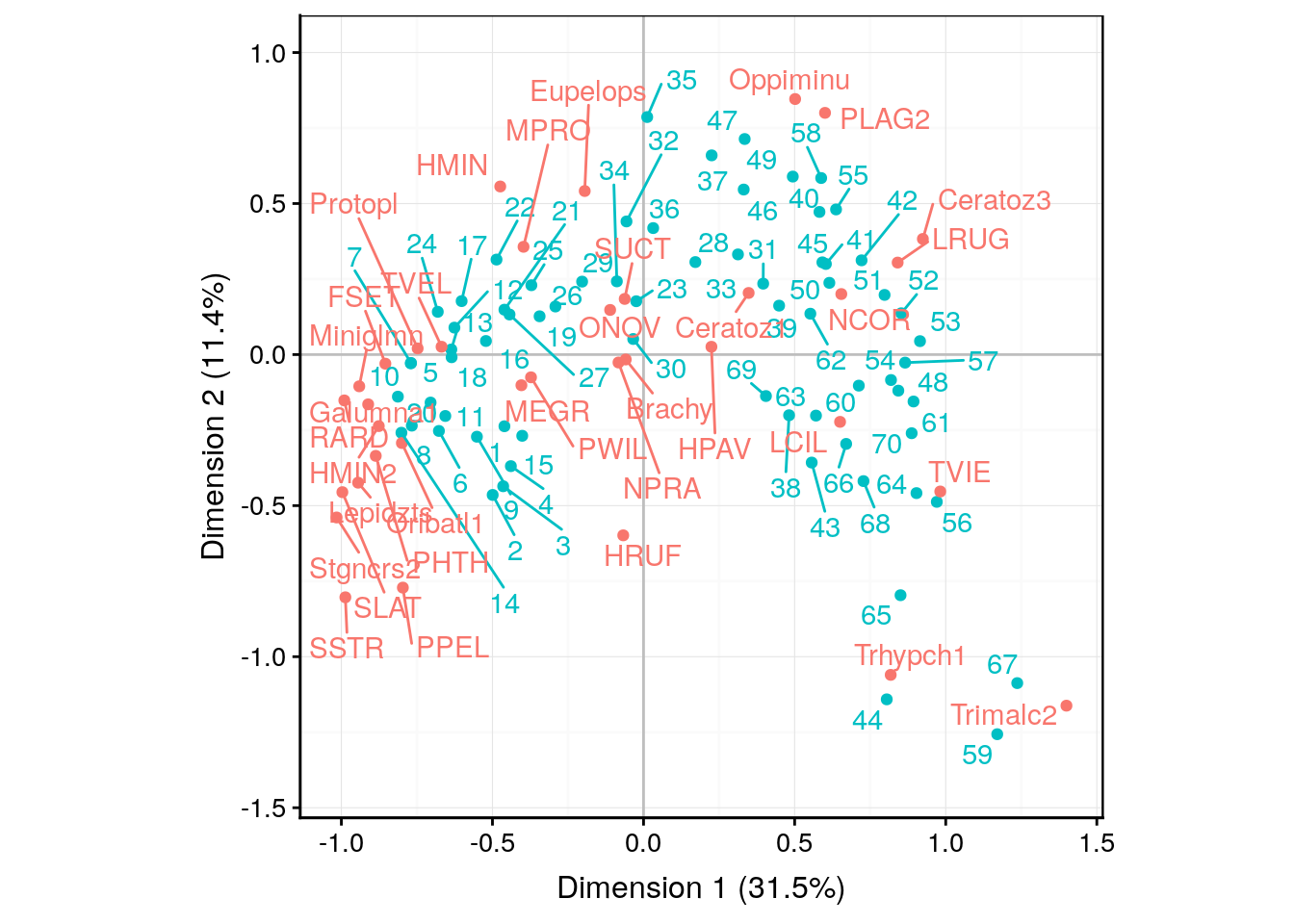
Nous vous laissons le soin d’effectuer l’analyse complète des points bleus (stations) entre eux, ensuite les points rouges (espèces) entre eux et enfin, conjointement. Notez les stations 44, 59, 65 et 67 qui se détachent et qui sont caractérisées par des espèces qu’on trouve préférentiellement là-bas : Trhypch1 et Trimalc2. Les espèces et station proches du centre d’inertie, au contraire, ne montrent aucune particularité.
7.2.4 Principe de l’AFC
Maintenant que nous avons découvert la façon de réaliser et d’interpréter une AFC, il est temps d’en comprendre les rouages. Rappelez-vous que la distance du Chi2 quantifie l’écart entre des effectifs observés \(a_i\) et des effectifs théoriques \(\alpha_i\) comme :
\[\chi^2=\sum{\frac{(a_i - \alpha_i)^2}{\alpha_i}}\]
Il y a un terme par cellule du tableau de contingence (que nous appelerons les contributions au Chi2), et par ailleurs, sous l’hypothèse nulle d’indépendance des variables, les \(\alpha_i\) sont connus et dépendent uniquement des sommes des lignes et des colonnes du tableau. En effet, nous avons :
\[\alpha_i = \frac{\textrm{total ligne} . \textrm{total colonne}}{\textrm{total général}}\]
Donc, lors du calcul du Chi2, nous passons par une étape de transformation du tableau de contingence à double entrée où nous substituons les effectifs observés (des entiers, donc du quantitatif discret) par les contributions respectives au Chi2. Or ces contributions sont des valeurs réelles (continues) nulles ou positives. Nous obtenons donc un tableau contenant des valeurs numériques continues qui peut être traité par une ACP classique.
L’ACP va reprojetter les lignes du tableau (qui, rappelons-le, sont les différents niveaux d’une des deux variables qualitative étudiée) dans un espace réduit. Dans ce contexte, le graphique représentant les variables n’a pas grand intérêt, puique ces variables sont en réalité fictives, ou si vous préférez, “bricolées”. Par contre, la position des individus les uns par rapport aux autres, et par rapport au centre d’inertie du graphique a une signification importante et interprétable.
Enfin, comme il n’y a aucune raison a priori d’utiliser une variable en ligne et l’autre en colonne, nous pouvons également transposer la table de contingence (les lignes deviennent les colonnes et vice versa). Si nous réalisons une nouvelle ACP sur ce tableau transposé, nous allons reprojetter les niveaux de l’autre variable qualitative sur un autre espace réduit.
Si nous prenons le même nombre de composantes principales des deux côtés, nous aurons la même part de variance reprise dans les deux projections. De plus, nous pouvons superposer les deux représentations en faisant coïncider les deux centres d’inertie en {0, 0}. La difficulté, comme pour tout biplot, est d’arriver à mettre à l’échelle les points d’une représentation par rapport à ceux de l’autre. Cette mise à l’échelle permet d’interpréter les points de couleurs différentes conjointement : des points proches sur le biplot dénotent des correspondances entre les niveaux respectifs des deux variables étudiées, d’où le nom de la méthode, analyse factorielle des correspondances.
Au final, l’AFC apparait donc comme une variante de l’ACP qui utilise la distance du Chi2 à la place de la distance euclidienne dans l’ACP classique, et qui reflète la symétrie du tableau de contingence (lignes/colonnes versus colonnes/lignes). Il en résulte la possiblité d’analyser ainsi des données qualitatives pour lesquelles la distance et la statistique du Chi2 ont précisément été inventées.
Pour en savoir plus
Une courte introduction de l’AFC en vidéo avec résolution d’un exemple volontairement simpliste pour faire comprendre la signification du graphique obtenu et la façon de l’interpréter.
Une autre explication qui utilise les packages
FactoMineRetfactoextraet qui va plus loin dans les concepts (notamment la qualité de la représentation des points via leur “cos2”, les différents types de biplots, et l’ajout de données supplémentaires).
A vous de jouer !
- Réalisez le début du projet spécifique lié au module 7. Ce module couvre la matière entière du module 7.
Le lien pour réaliser ce projet se trouve en début du module 7
Ce projet doit être terminé à la fin de ce module- Complétez votre projet sur le transect entre Nice et Calvi débuté lors du module 5. Lisez attentivement le README (Ce dernier a été mis à jour).
Complétez votre projet. Lisez attentivement le README.
La dernière version du README est disponible via le lien suivant :
Le README est un rappel des consignes, il ne s’agit aucunement du lien pour débuter le travailAttention : les valeurs sur les axes ne sont pas à interpréter quantitativement. Elles ne portent pas une information utile ici.↩