3.1 Histogramme

Vous souhaitez visualiser l’étalement de vos données sur un axe (on parle de distribution⁶ en statistique) pour l’une des variables étudiées. L’histogramme est l’un des graphiques qui vous apportent cette information de manière visuelle. Il représente sous forme de barres un découpage en plusieurs classes⁷ d’une variable numérique.

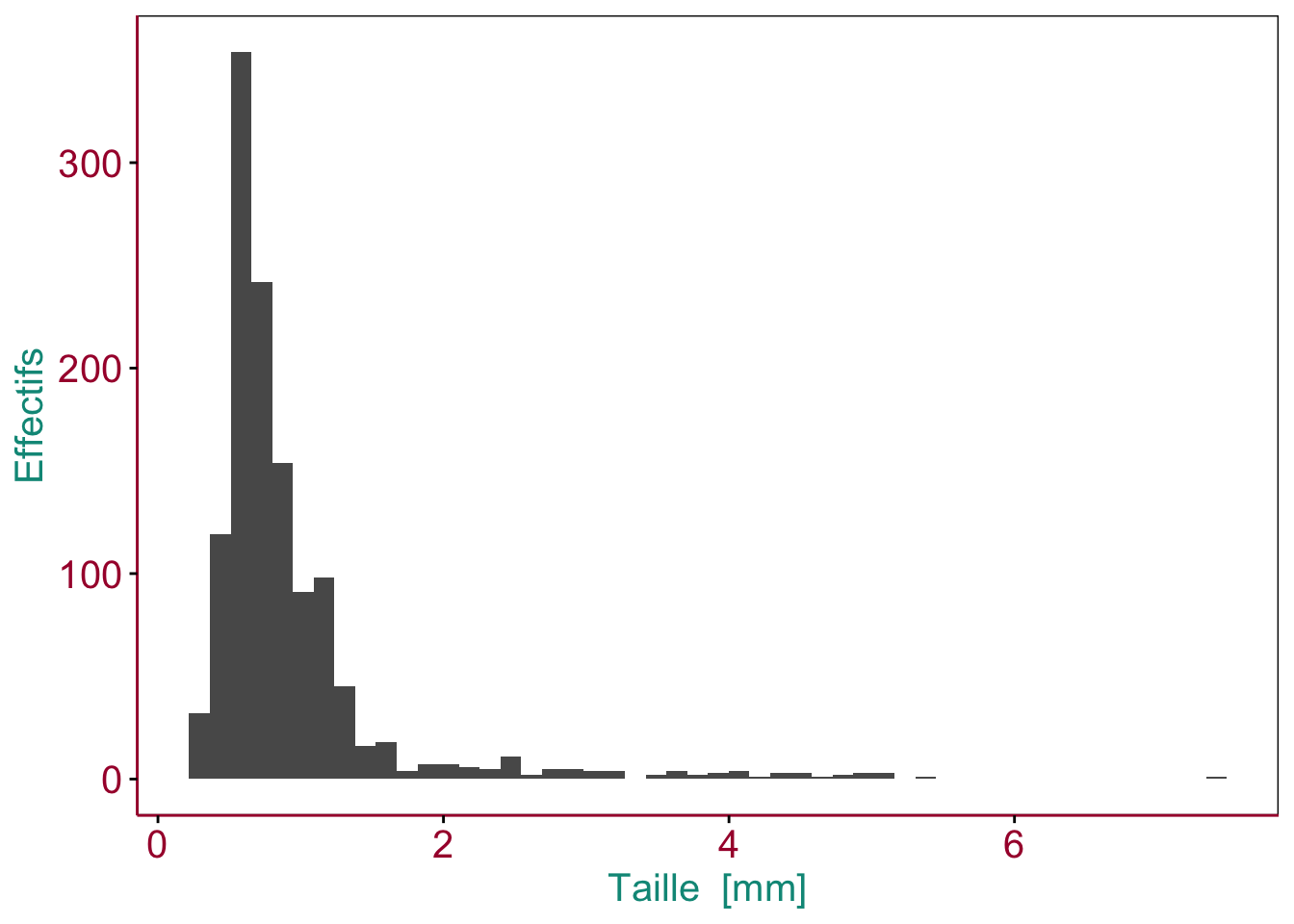
Figure 3.1: Exemple d’histogramme montrant la distribution de la taille dans un échantillon de zooplancton. Des couleurs sont utilisées pour mettre en évidence différentes parties du graphique (en pratique, les axes et leurs labels seront noirs).

Outre l’histogramme lui-même, représenté par des barres noires de hauteur équivalente au nombre d’observations dans les différentes classes, les éléments suivants sont également indispensables à la compréhension du graphique (ici mis en évidence en couleur) :

• Les axes avec les graduations (en rouge). Sur l’axe des abscisses, la variable numérique étudiée (ici la taille en mm), et sur l’axe des ordonnées, les effectifs
• les labels des axes et les unités (pour l’axe des abscisses uniquement ici) (en bleu)

Les instructions dans R pour produire un tel histogramme à l’aide de la fonction chart() sont :

# Importation du jeu de données
zooplankton <- read("zooplankton", package = "data.io", lang = "FR")
tabularise$headtail(zooplankton)

Diamètre circulaire équivalent [mm]	Aire [mm^2]	Périmètre [mm]	Diamètre de Feret [mm]	Axe majeur de l'ellipsoïde [mm]	Axe mineur de l'ellipsoïde [mm]	D.O. moyenne	D.O. plus fréquente	D.O. minimale	D.O. maximale	D.O. écart type	Etendue des D.O.	Taille [mm]	Ratio d'aspect	Elongation	Compacité	Transparence	Circularité	D.O. intégrée	Classe
0.7697829	0.4654	4.4469	1.3168	1.1640	0.5091	0.3631	0.036	0.004	0.908	0.2313	0.904	0.83655	0.4373711	8.504961	3.381259	0.0798124665	0.2958	0.1690	Poecilostomatoïde
0.7004136	0.3853	2.3247	0.7281	0.7128	0.6882	0.3609	0.492	0.024	0.676	0.1831	0.652	0.70050	0.9654882	1.000000	1.116156	0.0001233552	0.8959	0.1390	Oeuf_rond
0.8147804	0.5214	4.1509	1.3267	1.1106	0.5978	0.3082	0.032	0.008	0.696	0.2039	0.688	0.85420	0.5382676	6.097393	2.629685	0.0461479759	0.3803	0.1607	Calanoïde
0.7850146	0.4840	4.4422	1.7845	1.5641	0.3940	0.3317	0.036	0.004	0.728	0.2178	0.724	0.97905	0.2519021	8.068804	3.244449	0.1981874152	0.3082	0.1606	Poecilostomatoïde
0.3614338	0.1026	1.7065	0.7391	0.6940	0.1883	0.1526	0.016	0.008	0.452	0.1099	0.444	0.44115	0.2713256	4.891424	2.258683	0.1807009408	0.4429	0.0157	Harpacticoïde
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
0.5579490	0.2445	4.6214	0.9864	0.7318	0.4254	0.0329	0.012	0.004	0.300	0.0415	0.296	0.57860	0.5813064	19.787231	6.951178	0.0356913516	0.1438	0.0080	Poecilostomatoïde
0.4763311	0.1782	4.2148	0.9864	0.5593	0.4057	0.1474	0.016	0.004	0.508	0.1477	0.504	0.48250	0.7253710	22.878484	7.932980	0.0127853501	0.1261	0.0263	Calanoïde
0.5744769	0.2592	5.4060	0.9302	0.7010	0.4709	0.0374	0.012	0.004	0.304	0.0456	0.300	0.58595	0.6717546	26.149293	8.972371	0.0195803673	0.1115	0.0097	Poecilostomatoïde
0.6375093	0.3192	6.9642	1.6955	0.7468	0.5443	0.1576	0.008	0.004	0.600	0.1903	0.596	0.64555	0.7288431	35.957843	12.091209	0.0124556351	0.0827	0.0503	Calanoïde
0.5817449	0.2658	5.1730	1.0174	0.6401	0.5288	0.1292	0.008	0.004	0.536	0.1273	0.532	0.58445	0.8261209	23.125992	8.011616	0.0046285389	0.1248	0.0344	Calanoïde
Premières et dernières 5 lignes d'un total de 1262

# Réalisation du graphique
chart(data = zooplankton, ~ size) +
  geom_histogram(bins = 50) + # bins= nombre de classes souhaitées
  ylab("Effectifs")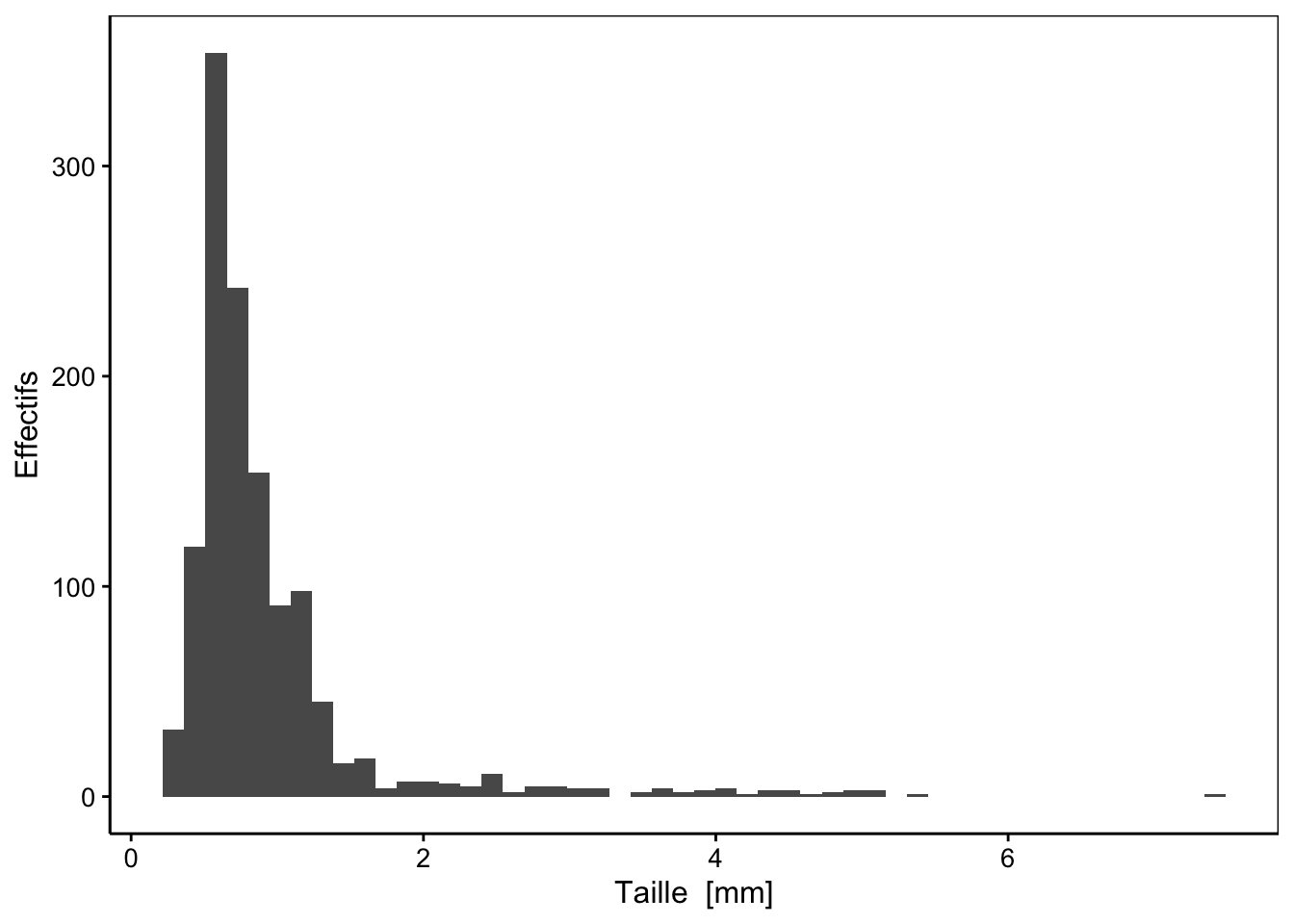

Figure 3.2: Distribution des tailles au sein d’un échantillon de zooplancton

La fonction chart() requiert comme argument le jeu de donnée (data = zooplankton), ainsi que la formule à employer dans laquelle vous avez indiqué le nom de la variable que vous voulez sur l’axe des abscisses à droite de la formule, après le tilde ~. Parmi toutes les variables du jeu de données, nous avons choisi ici de représenter size. Jusqu’ici, nous avons spécifié ce que nous voulons représenter, mais pas encore comment (sous quelle apparence), nous voulons matérialiser cela sur le graphique. Avec les graphiques de type ggplot() que nous réalisons ici à l’aide de chart(), nous ajoutons des couches au graphique à l’aide de l’opérateur +. Pour un histogramme, nous devons ajouter une couche avec la fonction geom_histogram(), tout comme pour le nuage de points, nous utilisions geom_point(). L’argument bins= dans cette fonction permet de préciser le nombre de classes souhaitées. Le découpage en classes de la variable size se fait ici automatiquement.

À vous de jouer !

Vous pouvez interpréter votre histogramme sur base des modes⁸ et de la symétrie⁹ de ces derniers. Un histogramme peut être unimodal (un seul mode), bimodal (deux modes) ou multimodal (plus de deux modes). En général, s’il y a plus d’un mode, nous pouvons suspecter que des sous-populations distinctes existent dans les données (par exemple des différences morphométriques entre mâles et femelles pour une espèce au dimorphisme sexuel marqué).

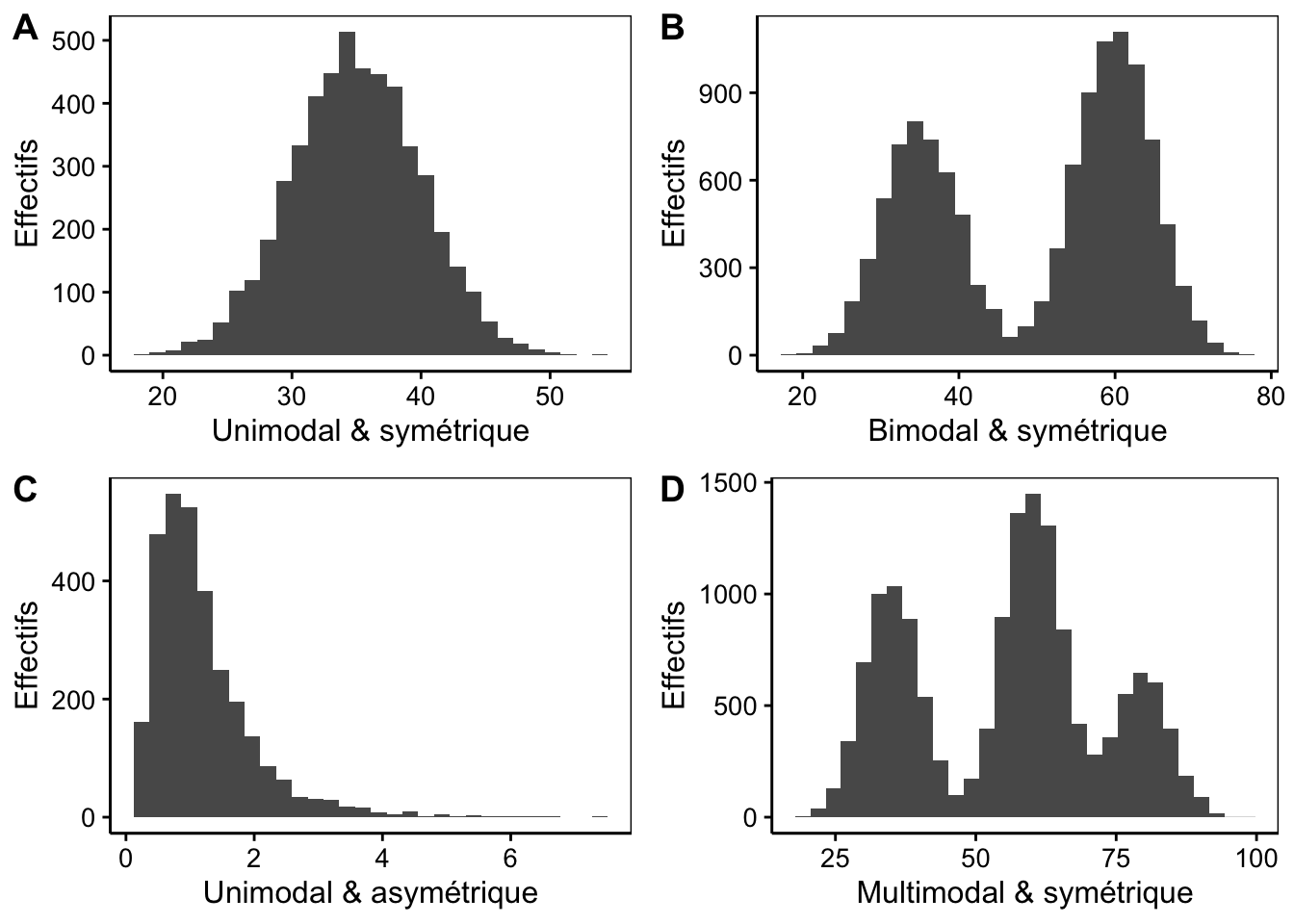
Figure 3.3: Histogrammes montrant les modes et symétries : A. histogramme unimodal et symétrique, B. histogramme bimodal et asymétrique, C. histogramme unimodal et asymétrique, D. histogramme multimodal et symétrique.

À vous de jouer !

3.1.1 Nombre de classes

Vous devez être particulièrement vigilant lors de la réalisation d’un histogramme aux classes définies pour ce dernier.

# Réalisation du graphique précédent
a <- chart(data = zooplankton, ~ size) +
  geom_histogram(bins = 50) +
  ylab("Effectifs")

# Modification du nombre de classes
b <- chart(data = zooplankton, ~ size) +
  geom_histogram(bins = 20) +
  ylab("Effectifs")

c <- chart(data = zooplankton, ~ size) +
  geom_histogram(bins = 10) +
  ylab("Effectifs")

d <- chart(data = zooplankton, ~ size) +
  geom_histogram(bins = 5) +
  ylab("Effectifs")

# Assemblage des graphiques
combine_charts(list(a, b, c, d))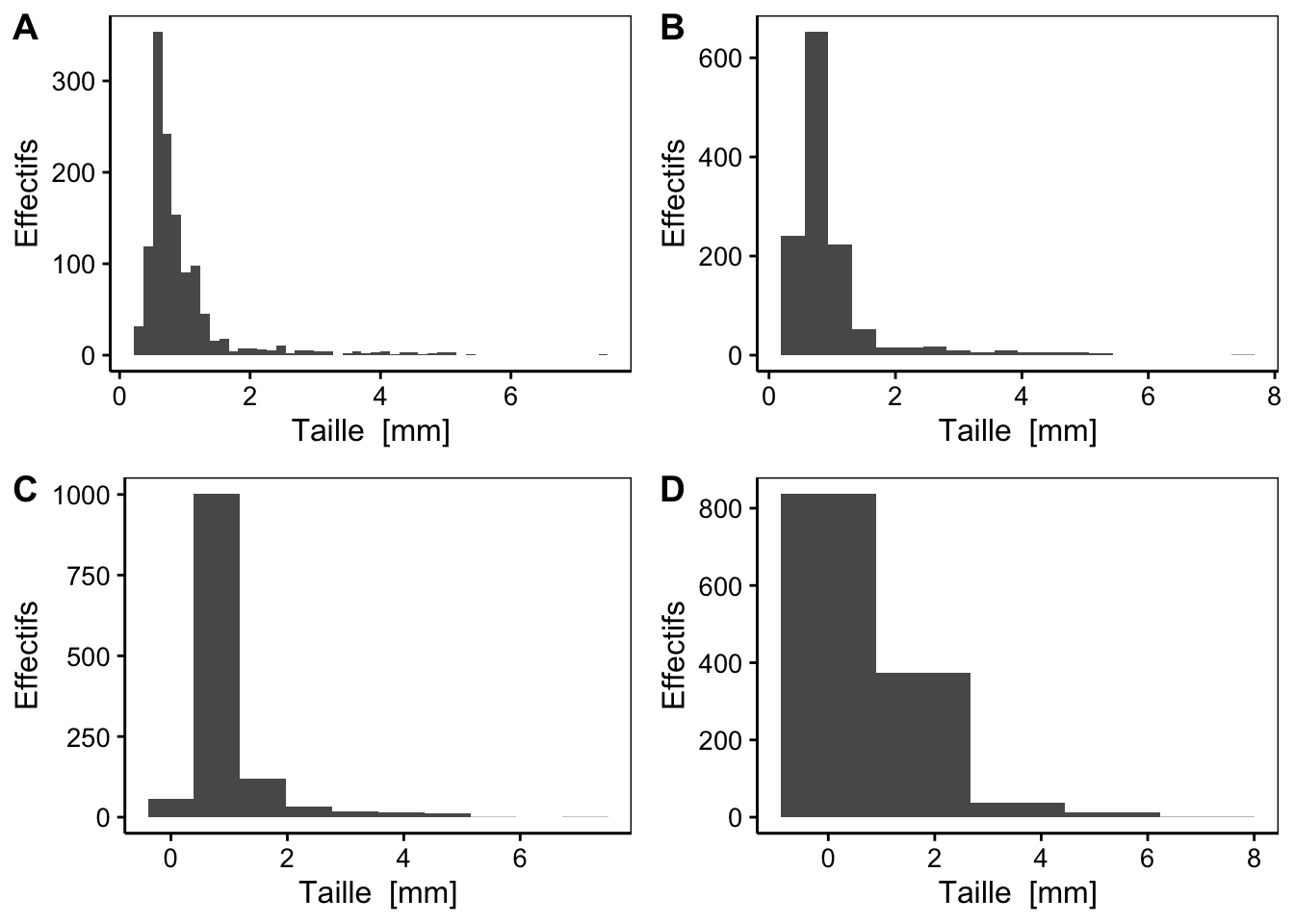

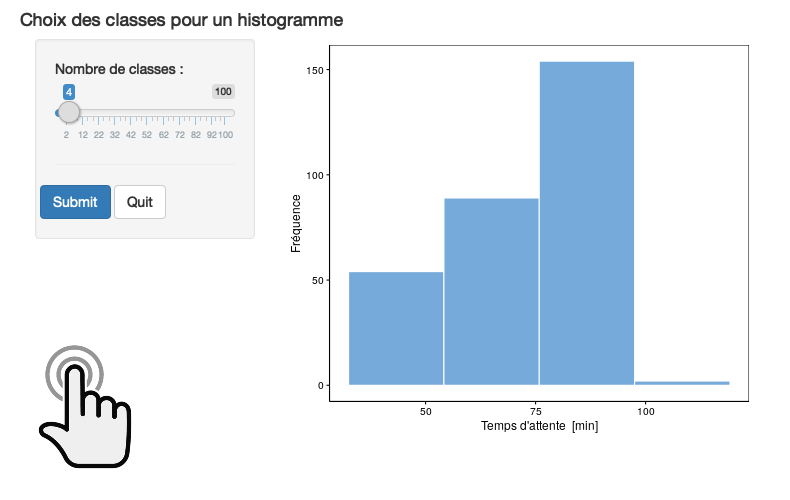
Figure 3.4: Choix des classes. A. histogramme initial montrant la répartition des tailles au sein d’organismes planctoniques. B., C., D. Même histogramme que A, mais en modifiant le nombre de classes.

Comme vous pouvez le voir à la Fig. 3.4, le changement du nombre de classes peut modifier complètement la perception des données au travers de l’histogramme (notez au passage l’utilisation de la fonction combine_charts() pour réaliser une figure composite, nous étudierons cette fonction plus en détail dans le prochain module). Le choix idéal est un compromis entre plus de classes (donc plus de détails), et un découpage raisonnable en fonction de la quantité de données disponibles. Si l’intervalle des classes est trop petit, l’histogramme sera illisible. Si l’intervalle des classes est trop grand, il sera impossible de visualiser correctement les différents modes. Dans la figure en exemple, les variantes A et B sont acceptables, mais les C et D manquent de détails.

À vous de jouer !

Cliquez pour lancer ou exécutez dans RStudio BioDataScience1::run_app("A03Sa_histogram").

Pièges et astuces

La SciViews Box propose un snippet RStudio pour réaliser un histogramme. Il s’appelle .cuhist (pour chart -> univariate -> histogram). Entrez ce code dans une zone d’édition R et appuyez ensuite sur la tabulation, et vous verrez le code remplacé par ceci :

chart(data = DF, ~VARNUM) +
  geom_histogram(binwidth = 30)

L’argument binwidth= permets de préciser la largeur des classes. C’est une autre façon de spécifier le découpage en classes, mais vous pouvez naturellement le remplacer par l’argument bins= comme nous l’avons faqit plus haut, si vous préférez.

Vous avez à votre disposition un ensemble de snippets que vous pouvez retrouver dans l’aide-mémoire sur SciViews. N’oubliez pas que vous avez également à votre disposition l’aide-mémoire sur la visualisation des données (Data Visualization Cheat Sheet), via la fonction ggplot() à laquelle vous pouvez simplement substituer chart().

3.1.2 Histogramme par facteur

Lors de l’analyse de jeux de données, vous serez amené à réaliser un histogramme par facteur (c’est-à-dire, en fonction de différents niveaux d’une variable qualitative qui divise le jeu de données en sous-groupes).

Une variable qualitative ou variable facteur est une variable qui représente des catégories. Par exemple, une couleur, le genre, une classe taxonomique… Les différentes catégories possibles pour la variable sont appelées niveaux ou modalités (levels en anglais). Pour le genre, par exemple, nous aurons deux niveaux (principaux) : “homme” ou “femme”.

Les variables facteurs peuvent aussi représenter un petit nombre de classes différentes. Une variable sera considérée comme qualitative ou facteur si elle possède moins d’une dizaine de niveaux pour fixer les idées, mais il n’existe pas de limite stricte entre une variable numérique quantitative et facteur qualitative, en réalité. C’est à votre appréciation, mais aussi en fonction du contexte. Une telle variable s’obtient par découpage d’une variable numérique. Par exemple, si au lieu de reprendre la taille d’un animal, nous nous contentons de déterminer s’il est “petit”, “moyen” ou “grand”. Dans ce cas, il existe un ordre logique entre les niveaux : petit < moyen < grand. La variable sera alors dite “qualitative ordonnée” et sera représentée par un objet ordered dans R. Sinon, la variable sera qualitative non ordonnée et sera un objet factor dans R.

Les variables numériques sont représentées par des nombres, donc numeric (des nombre décimaux à virgule flottante) ou integer (des entiers) dans R.

Attention que les variables facteur peuvent très bien être importées comme chaînes de caractères (objet character), et il faudra peut-être les convertir à l’aide des fonctions factor() ou ordered() avant de les utiliser.

Par exemple, dans un jeu de données sur des fleurs d’iris, la variable species¹⁰ représente l’espèce d’iris étudiée (trois espèces différentes : I. setosa, I. versicolor et I. virginica).

# Importation du jeu de données
iris <- read("iris", package = "datasets", lang = "fr")
tabularise$headtail(iris)

Longueur des sépales [cm]	Largeur des sépales [cm]	Longueur des pétales [cm]	Largeur des pétales [cm]	Espèces d'Iris
5.1	3.5	1.4	0.2	setosa
4.9	3.0	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
4.6	3.1	1.5	0.2	setosa
5.0	3.6	1.4	0.2	setosa
...	...	...	...	...
6.7	3.0	5.2	2.3	virginica
6.3	2.5	5.0	1.9	virginica
6.5	3.0	5.2	2.0	virginica
6.2	3.4	5.4	2.3	virginica
5.9	3.0	5.1	1.8	virginica
Premières et dernières 5 lignes d'un total de 150

# Réalisation de l'histogramme par facteur
chart(data = iris, ~ sepal_length %fill=% species) +
  geom_histogram(bins = 25) +
  ylab("Effectifs") +
  scale_fill_viridis_d() # palette de couleur harmonieuse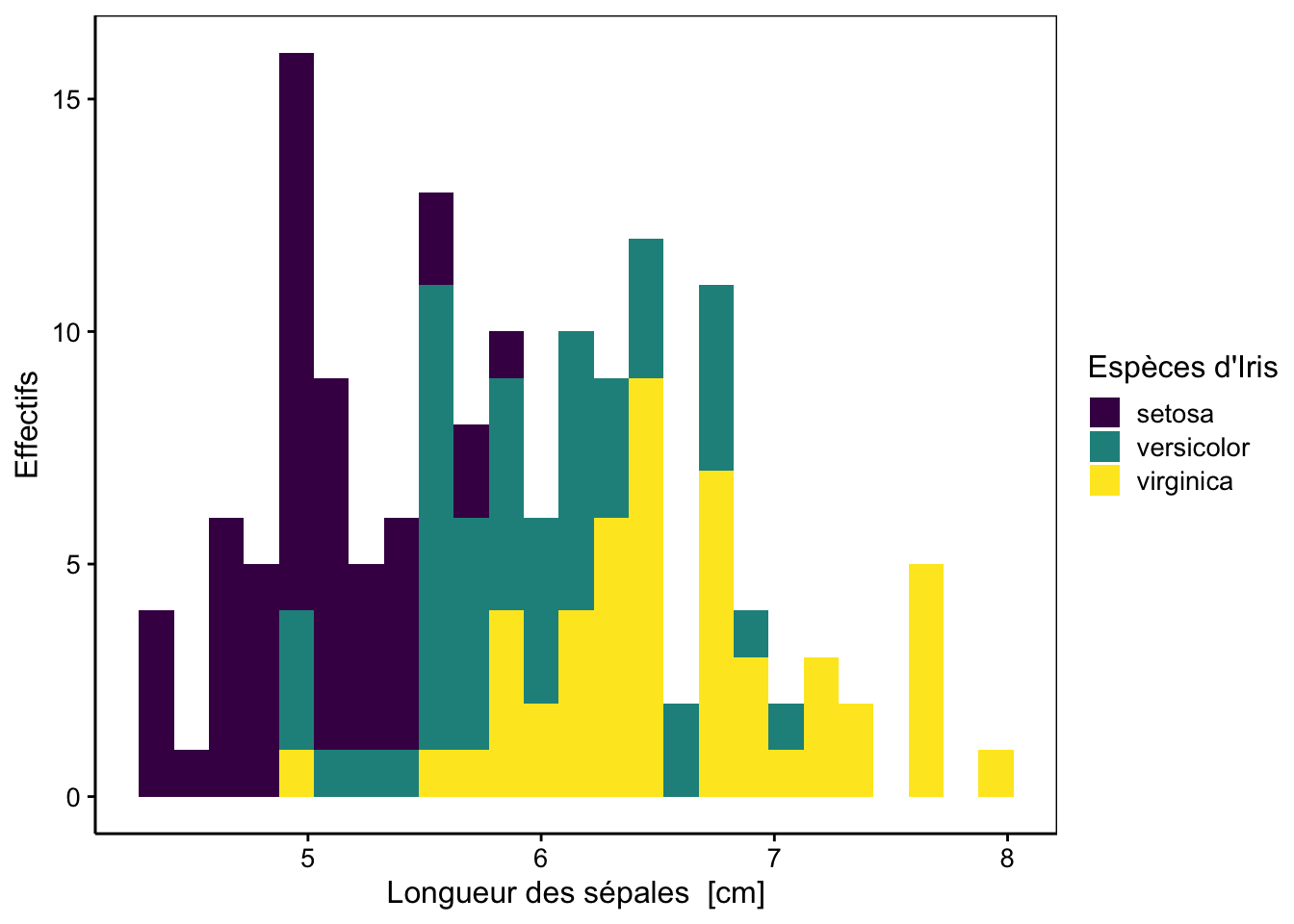

Figure 2.2: Distribution de la longueur des sépales de trois espèces d’iris.

Ici, nous avons tracé un histogramme unique, mais en prenant soin de colorier les barres en fonction de l’espèce. La formule fait toujours intervenir la variable numérique à découper en classes à la droite du tilde ~, ici sepal_length, mais nous y avons ajouté une directive supplémentaire pour indiquer que le remplissage des barres (%fill=%) doit se faire en fonction du contenu de la variable species.

Nous avons ici un bon exemple d’histogramme multimodal lié à la présence de trois sous-populations (les trois espèces différentes) au sein d’un jeu de données unique. Le rendu du graphique n’est pas optimal. Voici deux astuces pour l’améliorer. La première consiste à représenter trois histogrammes séparés, mais rassemblés dans une même figure. Pour cela, nous utilisons des facettes (facets) au lieu de l’argument %fill=%. Dans chart(), les facettes peuvent être spécifiées en utilisant l’opérateur | dans la formule.

iris <- read("iris", package = "datasets")
chart(data = iris, ~ sepal_length | species) +
  geom_histogram(bins = 25) +
  ylab("Effectifs")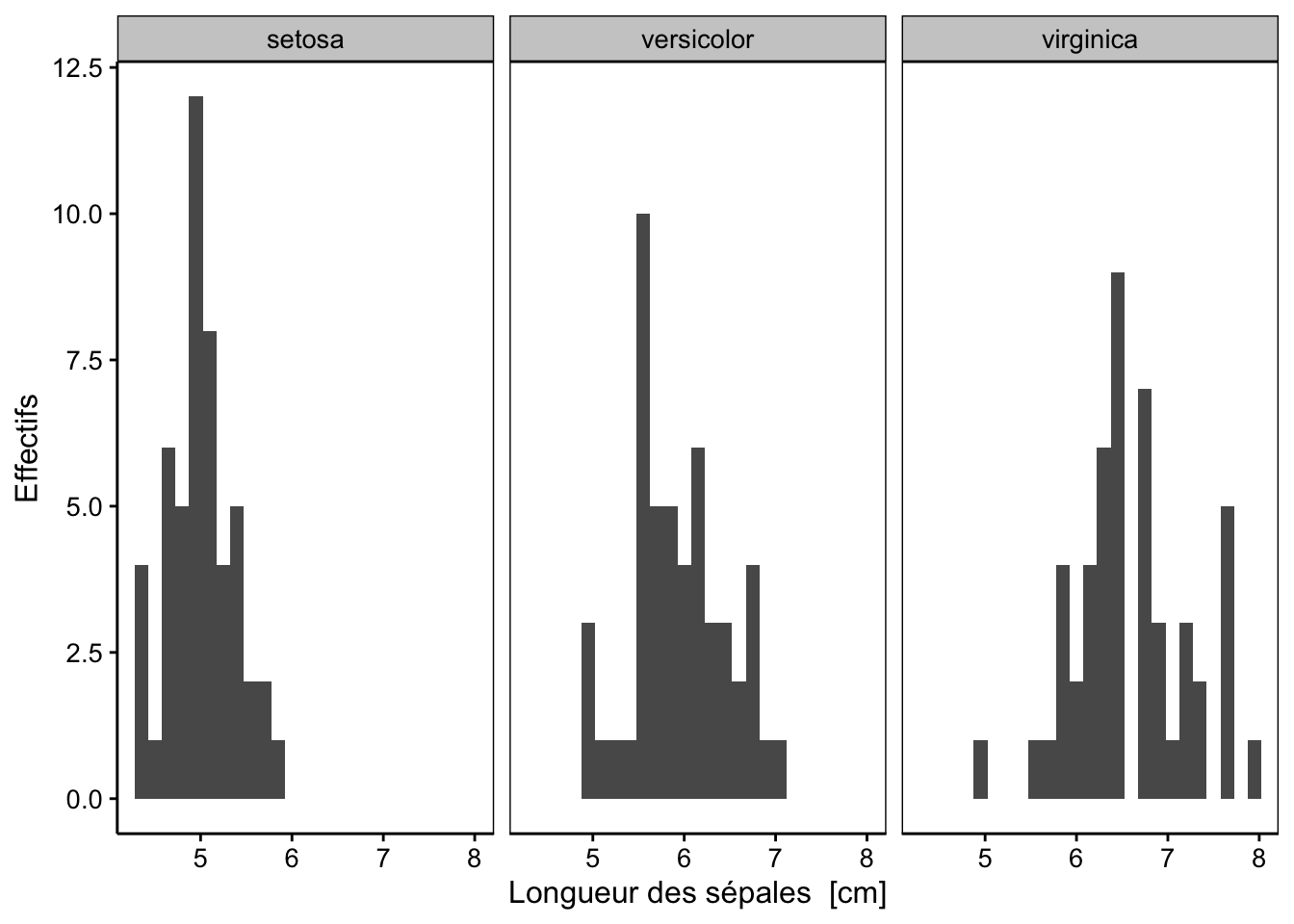

Figure 3.5: Distribution de la longueur des sépales de trois espèces d’iris (en employant les facettes pour séparer les espèces).

L’histogramme est maintenant séparé en trois en fonction des niveaux de la variable facteur species. Cela rend la lecture plus aisée. Une seconde solution combine les facettes avec | et l’argument %fill=%¹¹. Il faut ensuite ajouter par derrière un histogramme grisé de l’ensemble des données.

nbins <- 25
chart(data = iris, ~ sepal_length %fill=% species | species) +
  # histogramme d'arrière-plan en gris de toutes les données
  geom_histogram(data = sselect(iris, -species),
    fill = "grey", bins = nbins) + 
  # histogrammes par espèce
  geom_histogram(show.legend = FALSE, bins = nbins) +
  ylab("Effectifs") +
  scale_fill_viridis_d()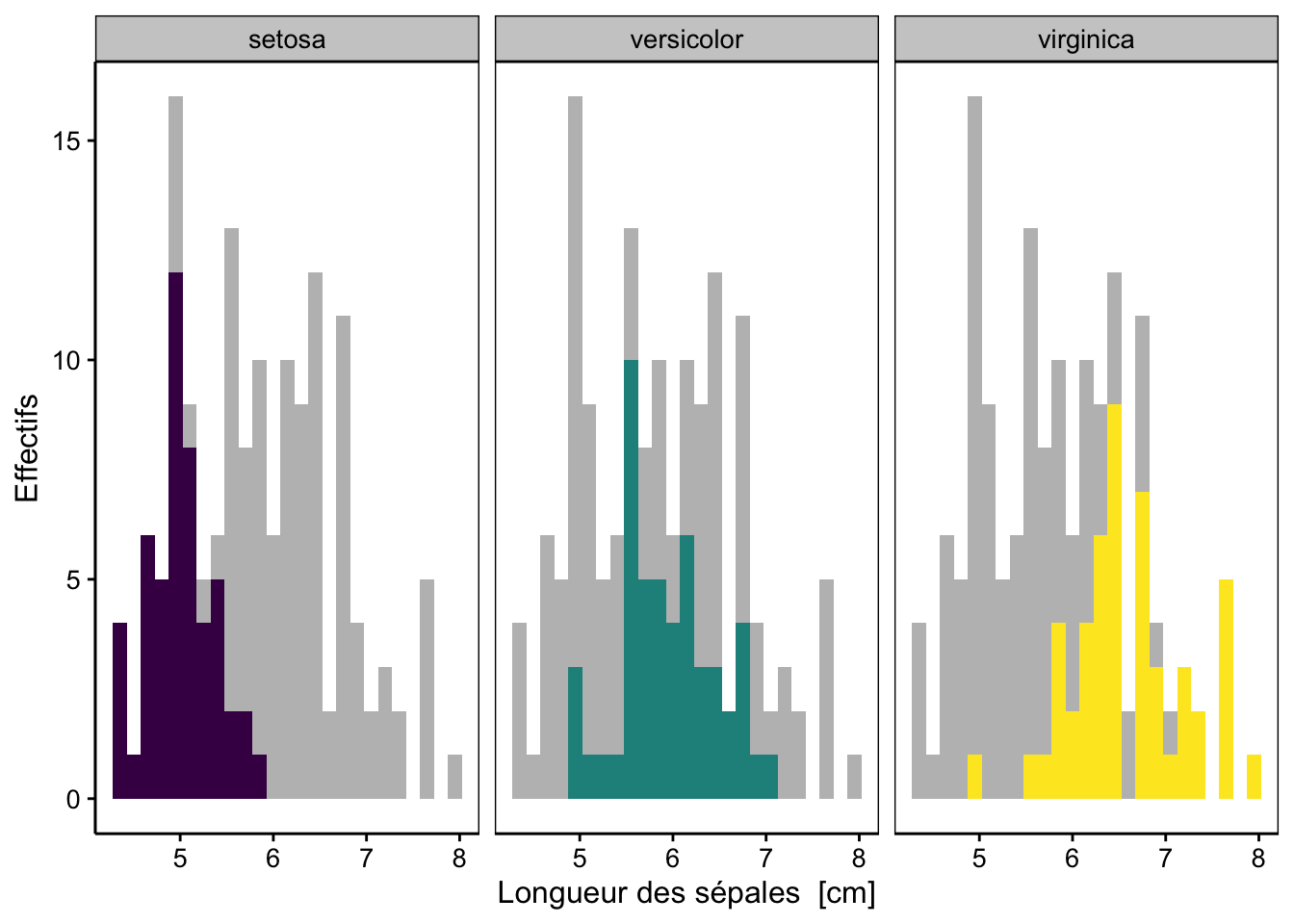

Figure 3.6: Distribution des longueurs de sépales de trois espèces d’iris (avec facettes et histogrammes complets grisés en arrière-plans).

Vous découvrez sans doute que les graphiques réalisables avec R sont modulables à souhait en ajoutant une série d’instructions successives qui créent autant de couches superposées dans le graphique. Cette approche permet de réaliser quasiment une infinité de graphiques différents en combinant quelques dizaines d’instructions. Pour s’y retrouver, les fonctions qui ajoutent des couches commencent toutes par geom_, et celles qui manipulent les couleurs par scale_, par exemple. Vous découvrirez encore d’autres fonctions graphiques plus loin.

À vous de jouer !

Effectuez maintenant les exercices du tutoriel A03La_univariate (Graphiques univariés).

BioDataScience1::run("A03La_univariate")

Note : Ce tutoriel couvre l’ensemble de la matière de ce module. N’hésitez pas à le réaliser en parallèle de votre lecture.

---

6. La distribution des données en statistique se réfère à la fréquence avec laquelle les différentes valeurs d’une variable s’observent.↩︎

7. Une variable numérique est découpée en classes en spécifiant différents intervalles, et ensuite en dénombrant le nombre de fois que les observations rentrent dans ces intervalles.↩︎

8. Les modes d’un histogramme correspondent à des classes plus abondantes localement, c’est-à-dire que les classes à gauche et à droite du mode comptent moins d’occurrences que lui.↩︎

9. Un histogramme est dit symétrique lorsque son profil à gauche est identique ou très similaire à son profil à droite autour d’un mode.↩︎

10. Attention : le jeu de donnée iris est un grand classique dans R, mais lorsqu’il est chargé à l’aide de la fonction read() du package {data.io}, le nom de ses variables est modifié pour suivre la convention “snake_case” qui veut que seules des lettres minuscules soient utilisées et que les mots soient séparés par un trait souligné _. Ainsi, dans le jeu de données d’origine, les variables sont nommées Petal.Length ou Species. Ici, ces mêmes variables se nomment petal_length et species.↩︎

11. Astuce proposée ici.↩︎