7.4 Distribution binomiale
Partons d’un exemple pratique pour découvrir la distribution binomiale. La mucoviscidose est, dans la population européenne, la plus fréquente des maladies génétiques héréditaires. Elle se caractérise par un mucus dans les voies respiratoires anormalement épais qui est à l’origine de diverses complications. L’altération d’une protéine CFTR est à l’origine de cette maladie. Comme le gène qui code pour cette protéine est récessif, il faut que les deux allèles soient porteurs simultanément de la mutation pour que la maladie apparaisse. Parmi des familles de six enfants dont le père et la mère normaux sont tous deux porteurs hétérozygotes du gène altéré, quelle est la probabilité d’obtenir 0, 1, 2, …, 6 enfants atteints de mucoviscidose ?
7.4.1 Épreuve de Bernoulli
La distribution binomiale est une loi de distribution discrète qui répond à ce genre de question. Ses conditions d’applications sont :
- résultats binaires (deux évènements disjoints possibles uniquement ; l’un sera nommé “succès” et l’autre “échec” par convention),
- essais indépendants (les probabilités ne changent pas d’un essai à l’autre),
- n, le nombre d’essais totaux, est fixé à l’avance,
- probabilité du “succès” p constante (probabilité de l’“échec” = 1 - p).
Les conditions particulières de cette situation sont appelées épreuve de Bernoulli. Mathématiquement, nous l’écrirons comme suit. Soit une variable aléatoire \(Y\) qui comptabilise le nombre de succès, la probabilité d’obtenir \(j\) succès parmi \(n\) essais est :
\[P(Y=j)= C^j_n \times p^j \times (1-p)^{n-j}\]
Le coefficient binomial \(C^j_n\) vaut33 : \[C^j_n = \frac{n!}{j!(n-j)!}\]
\(C^j_n\) représente le nombre de combinaisons possibles pour obtenir \(j\) succès parmi \(n\) essais réalisés dans un ordre quelconque. Nous pourrons aussi écrire :
\[Y \sim B(n,p)\]
Notre exemple de la mucoviscidose au sein d’une famille dont les parents sont tous deux hétérozygotes rentre parfaitement dans le cadre de l’épreuve de Bernoulli avec n = 6 et p, la probabilité du succès, c’est-à-dire, d’avoir un enfant qui ne développe pas la maladie, de 3/4 ou 0.75 : \(Y \sim B(6, 0.75)\).
7.4.2 Calculs et graphiques
Les calculs sur base d’une distribution binomiale sont assez similaires à ceux de la distribution uniforme dans R, en remplaçant unif par binom dans le nom des fonctions p/q/r/d. Sinon, la fonction dist_binomial(size = 6, prob = 0.75) la crée. Puisqu’il s’agit d’une distribution discrète, un petit nombre d’évènements possibles existent. Il est assez facile de créer une table qui reprend l’ensemble des probabilités possibles :
# succès probabilité
# 1: 0 0.0002441406
# 2: 1 0.0043945312
# 3: 2 0.0329589844
# 4: 3 0.1318359375
# 5: 4 0.2966308594
# 6: 5 0.3559570312
# 7: 6 0.1779785156La représentation graphique donne la Fig. 7.6.
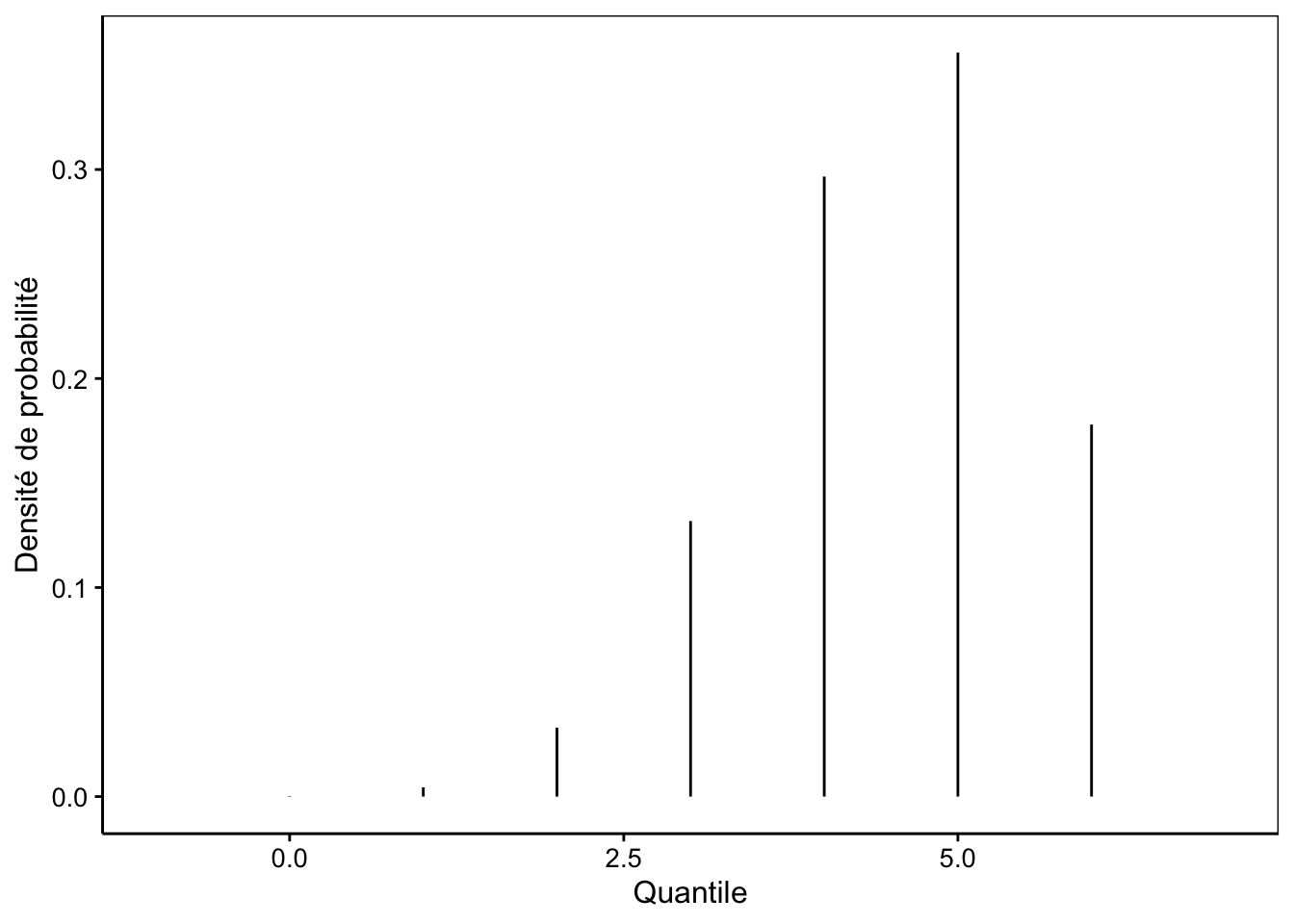
Figure 7.6: Probabilité d’avoir j enfants sains parmi 6 dans des familles dont les deux parents sont porteurs hétérozygotes du gène de la mucoviscidose.
La situation la plus probable est donc d’avoir cinq enfants sains sur six. Nous pouvons aussi observer que, lorsque \(p\) s’éloigne de 0.5, les probabilités à l’extrême opposé tendent assez rapidement vers zéro (ici, la probabilité de n’avoir qu’un seul, ou aucun enfant sain). La distribution binomiale trouve de très nombreuses applications en biologie, en écologie, en génétique et dans d’autres disciplines. Elle permet même de représenter vos chances de réussite à l’examen de science des données biologiques ! Voici, pour finir, l’allure d’une distribution binomiale pour laquelle la probabilité du succès est égale à la probabilité d’échec (0.5). Cette distribution est symétrique.
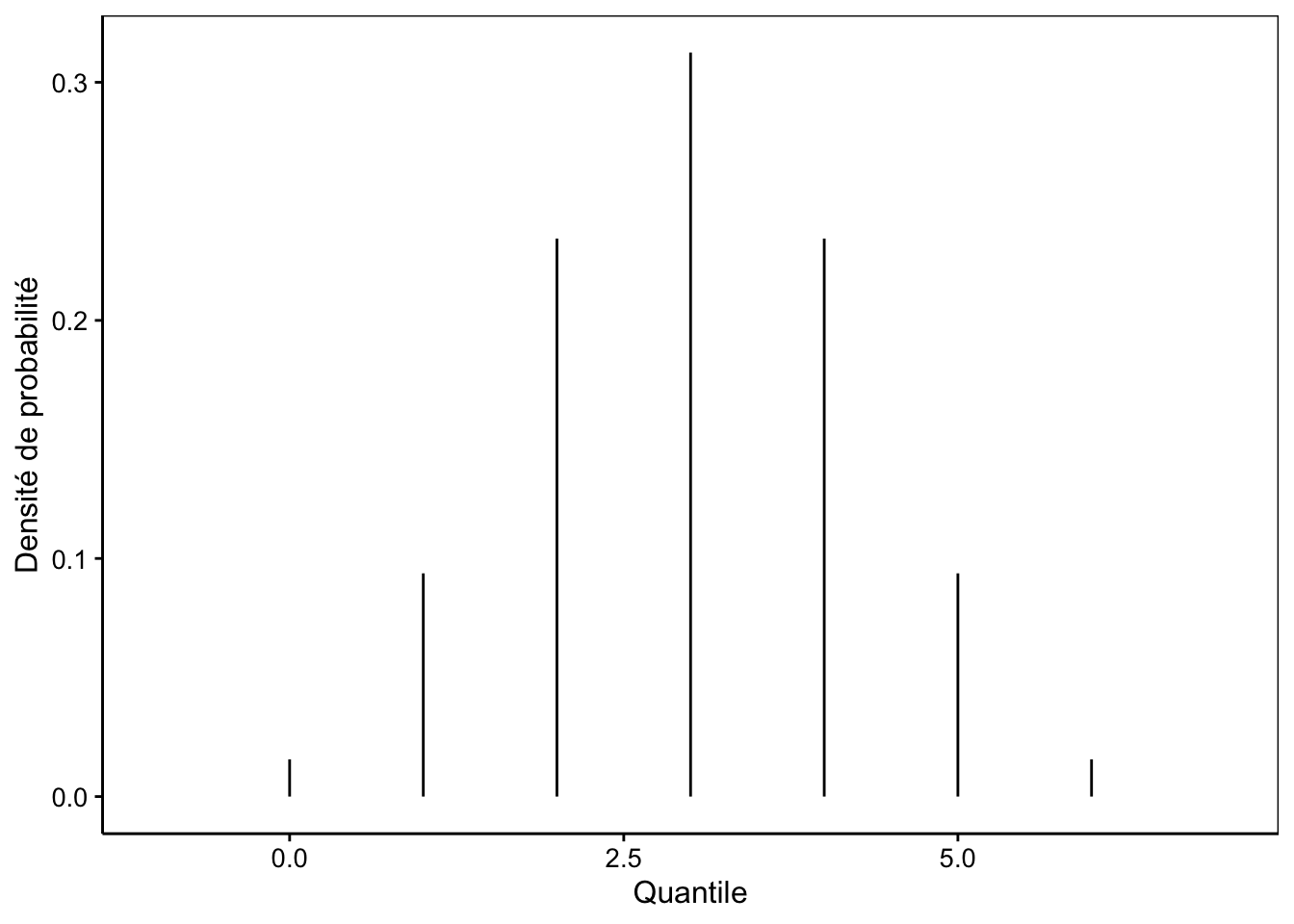
Figure 7.7: Probabilité d’avoir des garçons parmi une fratrie de 6 enfants (si le sexe ratio de 1:1).
Le factoriel d’un nombre \(n\), noté \(n!\) est \(1 \times 2 \times 3 \times ... \times n\), avec \(0! = 1\).↩︎