7.6 Distribution normale
La vidéo suivante vous permettra de récapituler certaines notions étudiées jusqu’ici concernant les types de variables et vous introduira la loi de distribution normale ou distribution de Gauss ou encore, gaussienne.
7.6.1 Une “courbe en cloche”
La distribution normale est la distribution la plus utilisée en statistique. Elle se rencontre très souvent en biologie comme dans bien d’autres domaines, à chaque fois qu’une variable continue définie sur tout le domaine des réels est issue d’un nombre important de composantes indépendantes dont les effets sont additifs. La forme de sa densité de probabilité est caractéristique et dite “en cloche” (Fig. 7.9).
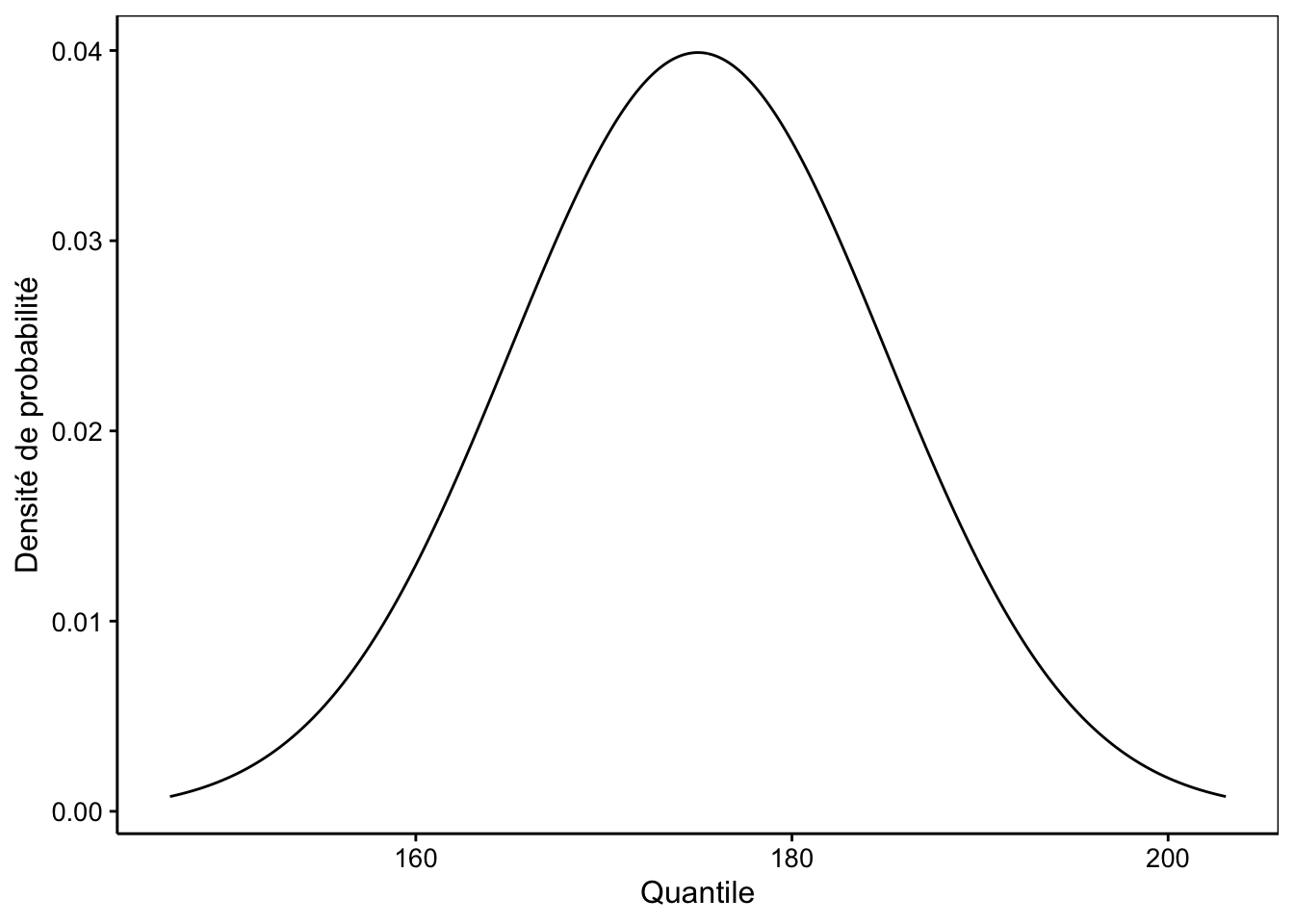
Figure 7.9: Un exemple de distribution normale.
Il s’agit d’une densité de probabilité symétrique et asymptotique à ses deux extrémités en \(+\infty\) et \(-\infty\). La distribution normale a deux paramètres : la moyenne \(\mu\) et l’écart type \(\sigma\). Sa densité de probabilité est représentée par l’équation suivante :
\[\Phi(Y) = \frac{1}{ \sigma \sqrt{2 \pi}} e^{-\frac{1}{2} \left( \frac{Y - \mu}{\sigma} \right)^2}\]
Pour une variable aléatoire \(Y\) qui suit une distribution normale avec une moyenne \(\mu\) et un écart type \(\sigma\), nous considérons généralement le carré de l’écart type qui est la variance, notée \(\sigma^2\) :
\[Y \sim N(\mu, \sigma^2)\]
À noter que l’on rencontre aussi profois la notation utilisant l’écart type ou lieu de la variance, donc \(Y \sim N(\mu, \sigma)\).
7.6.2 Loi normale réduite
Parmi toutes les distributions normales possibles, l’une d’entre elles est particulière : la distribution normale réduite qui a toujours une moyenne nulle et une variance, et donc un écart type unitaire.
\[N(0, 1)\]
Elle représente la distribution des valeurs pour une variable qui a été standardisée, c’est-à-dire, à laquelle on a soustrait la moyenne et que l’on a divisée par son écart type.
\[Z = \frac{Y - \mu}{\sigma}\]
Sa formulation est nettement simplifiée par rapport à la distribution normale :
\[\Phi(Z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{Z^2}{2}}\]
La probabilité qu’une observation soit dans un intervalle de \(\pm 1 \sigma\) autour de la moyenne est de 2/3 environ. De même, un intervalle de \(\pm 2 \sigma\) définit une aire de 95%, et celle-ci devient supérieure à 99% pour des observations qui se situent dans l’intervalle \(\pm 3 \sigma\) (Fig. 7.10).
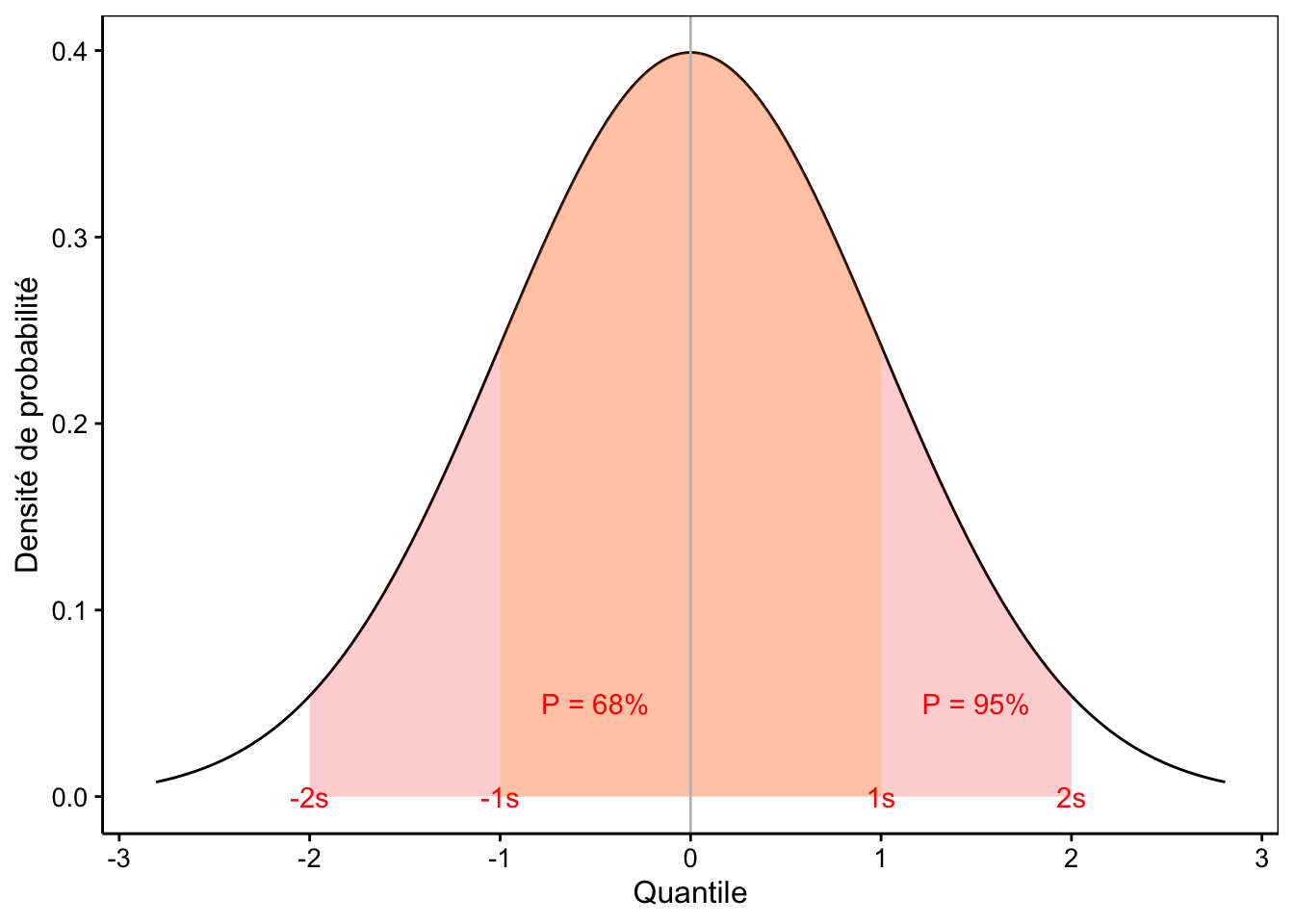
Figure 7.10: La distribution normale réduite avec les aires centrales autour de 1 et 2 écarts types mises en évidence.
7.6.3 Fonctions dans R pour la normale
Les fonctions p/q/r/d relatives à la distribution normale dans R sont composées du suffixe norm. Le calcul de probabilités se fait à l’aide de pnorm(), de quantiles à partir de qnorm(). Un échantillon pseudo-aléatoire s’obtient à partir de rnorm(). L’objet distribution s’obtient avec dist_normal(mu =..., sigma = ...). Faites bien attention que les arguments équivalents dans les fonctions p/q/r/d sont mean = et sd =. Dans les deux cas, il s’agit de la moyenne et de l’écart type de la distribution qui sont ses deux paramètres. De plus, le nom formaté de la distribution reprend la variance à la place de l’écart type (variance = écart type2). Cela donne donc :
N1 <- dist_normal(mu = 12, sigma = 1.5) # Arguments mu =, sigma =
N1 # Attention: N(mu, variance) 1.5^2 = 2.2# <distribution[1]>
# [1] N(12, 2.2)# [1] 14.46728# [1] 14.467287.6.4 Théorème central limite
Une des raisons pour lesquelles la distribution normale est très répandue est liée au fait que beaucoup d’autres distributions tendent vers elle de manière asymptotique. Par exemple, une distribution binomiale symétrique (avec \(p = 0.5\)) et pour un \(n\) croissant ressemblera de plus en plus à une distribution normale. Le théorème central limite démontre cela, quelle que soit la distribution de départ. En pratique, la distribution normale est souvent une bonne approximation d’autres distributions pour des tailles d’échantillons déjà à partir de quelques dizaines d’individus.