4.1 Graphique en barres
Le graphique en barres (on dit aussi graphique en bâtons) compare les effectifs pour différents niveaux (ou modalités) d’une variable qualitative ou facteur. La différence avec l’histogramme est donc subtile et tient au fait que, pour l’histogramme, nous partons d’une variable quantitative qui est découpée en classes.
4.1.1 Effectifs par facteur
La question du nombre et/ou de l’intervalle des classes ne se pose pas dans le cas du graphique en barres. Par défaut, les barres seront séparées les unes des autres par un petit espace vide pour bien indiquer visuellement qu’il n’y a pas continuité entre les classes (dans l’histogramme, les barres sont accolées les unes aux autres pour matérialiser justement cette continuité).
La formule que vous utiliserez, ici encore, ne fait appel qu’à une seule variable et s’écrira donc :
\[\sim variable \ facteur\]
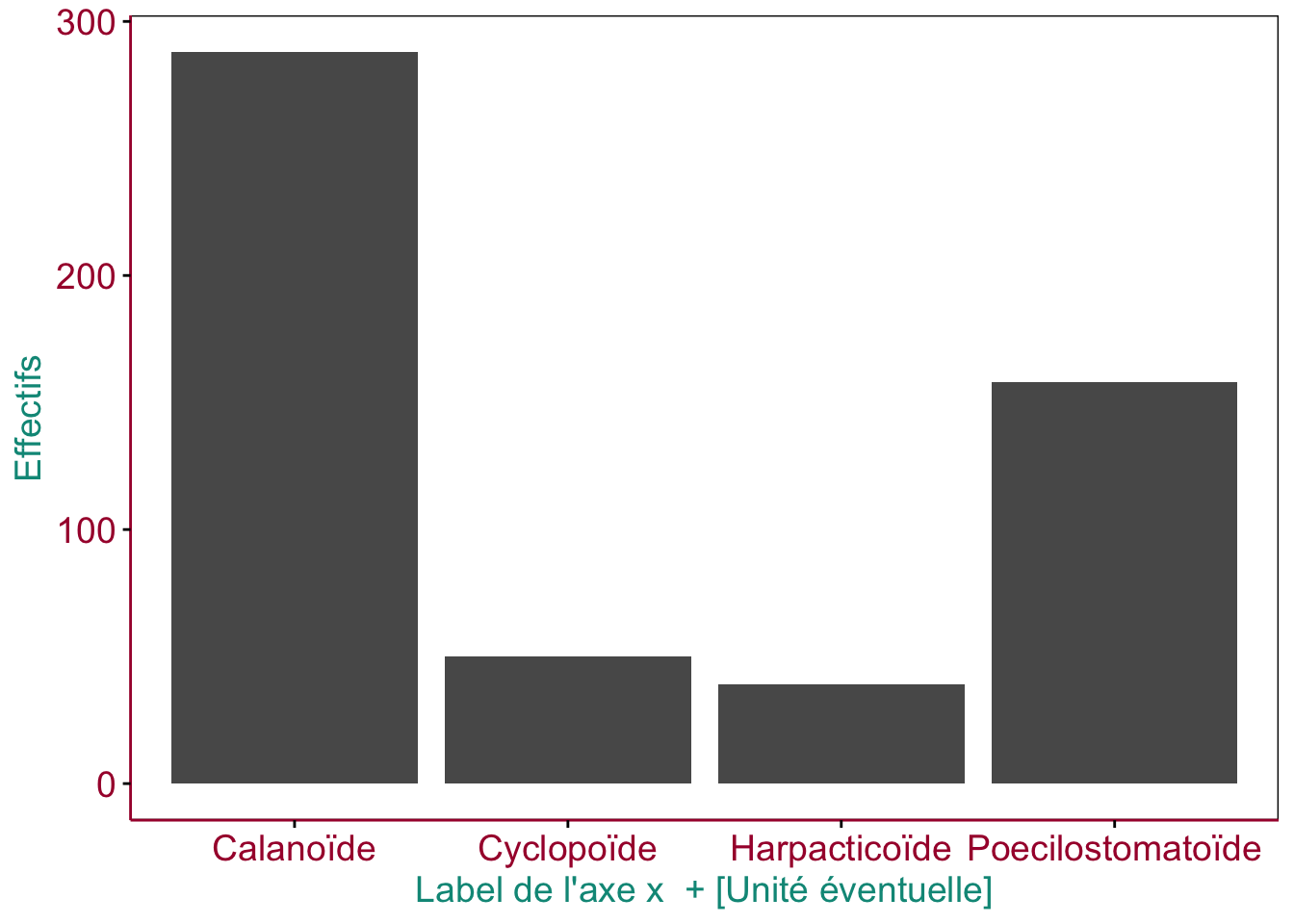
Figure 4.1: Exemple d’un graphique en barres montrant le dénombrement des niveaux d’une variable facteur, avec les éléments importants du graphique mis en évidence en couleurs.
Outre les barres elles-mêmes, prêtez toujours attention aux éléments suivants du graphique (ici mis en évidence en couleurs) :
- les axes avec les graduations (en rouge)
- les niveaux de la variable facteur (en rouge également)
- le label des axes (en bleu)
Les instructions dans R pour produire un graphique en barres à l’aide de la fonction chart() sont les suivantes. Nous partons d’un jeu de données zooplankton que nous importons et dont nous extrayons un sous-ensemble à l’aide de la fonction sfilter() (vous étudierez en détail les fonctions de remaniement de tableaux dans les deux prochains modules) avant de réaliser notre graphique à l’aide de chart() :
# Importation du jeu de données
(zooplankton <- read("zooplankton", package = "data.io", lang = "FR"))# ecd area perimeter feret major minor mean mode min max
# 1: 0.7697829 0.4654 4.4469 1.3168 1.1640 0.5091 0.3631 0.036 0.004 0.908
# 2: 0.7004136 0.3853 2.3247 0.7281 0.7128 0.6882 0.3609 0.492 0.024 0.676
# 3: 0.8147804 0.5214 4.1509 1.3267 1.1106 0.5978 0.3082 0.032 0.008 0.696
# 4: 0.7850146 0.4840 4.4422 1.7845 1.5641 0.3940 0.3317 0.036 0.004 0.728
# 5: 0.3614338 0.1026 1.7065 0.7391 0.6940 0.1883 0.1526 0.016 0.008 0.452
# ---
# 1258: 0.5579490 0.2445 4.6214 0.9864 0.7318 0.4254 0.0329 0.012 0.004 0.300
# 1259: 0.4763311 0.1782 4.2148 0.9864 0.5593 0.4057 0.1474 0.016 0.004 0.508
# 1260: 0.5744769 0.2592 5.4060 0.9302 0.7010 0.4709 0.0374 0.012 0.004 0.304
# 1261: 0.6375093 0.3192 6.9642 1.6955 0.7468 0.5443 0.1576 0.008 0.004 0.600
# 1262: 0.5817449 0.2658 5.1730 1.0174 0.6401 0.5288 0.1292 0.008 0.004 0.536
# std_dev range size aspect elongation compactness transparency
# 1: 0.2313 0.904 0.83655 0.4373711 8.504961 3.381259 0.0798124665
# 2: 0.1831 0.652 0.70050 0.9654882 1.000000 1.116156 0.0001233552
# 3: 0.2039 0.688 0.85420 0.5382676 6.097393 2.629685 0.0461479759
# 4: 0.2178 0.724 0.97905 0.2519021 8.068804 3.244449 0.1981874152
# 5: 0.1099 0.444 0.44115 0.2713256 4.891424 2.258683 0.1807009408
# ---
# 1258: 0.0415 0.296 0.57860 0.5813064 19.787231 6.951178 0.0356913516
# 1259: 0.1477 0.504 0.48250 0.7253710 22.878484 7.932980 0.0127853501
# 1260: 0.0456 0.300 0.58595 0.6717546 26.149293 8.972371 0.0195803673
# 1261: 0.1903 0.596 0.64555 0.7288431 35.957843 12.091209 0.0124556351
# 1262: 0.1273 0.532 0.58445 0.8261209 23.125992 8.011616 0.0046285389
# circularity density class
# 1: 0.2958 0.1690 Poecilostomatoïde
# 2: 0.8959 0.1390 Oeuf_rond
# 3: 0.3803 0.1607 Calanoïde
# 4: 0.3082 0.1606 Poecilostomatoïde
# 5: 0.4429 0.0157 Harpacticoïde
# ---
# 1258: 0.1438 0.0080 Poecilostomatoïde
# 1259: 0.1261 0.0263 Calanoïde
# 1260: 0.1115 0.0097 Poecilostomatoïde
# 1261: 0.0827 0.0503 Calanoïde
# 1262: 0.1248 0.0344 Calanoïde# Réduction du jeu de données à quatre classes seulement
(copepoda <- sfilter(zooplankton, class %in% c("Calanoïde", "Cyclopoïde",
"Harpacticoïde", "Poecilostomatoïde")))# ecd area perimeter feret major minor mean mode min max
# 1: 0.7697829 0.4654 4.4469 1.3168 1.1640 0.5091 0.3631 0.036 0.004 0.908
# 2: 0.8147804 0.5214 4.1509 1.3267 1.1106 0.5978 0.3082 0.032 0.008 0.696
# 3: 0.7850146 0.4840 4.4422 1.7845 1.5641 0.3940 0.3317 0.036 0.004 0.728
# 4: 0.3614338 0.1026 1.7065 0.7391 0.6940 0.1883 0.1526 0.016 0.008 0.452
# 5: 0.8324043 0.5442 5.2658 1.6554 1.3564 0.5109 0.3711 0.020 0.004 0.844
# ---
# 531: 0.5579490 0.2445 4.6214 0.9864 0.7318 0.4254 0.0329 0.012 0.004 0.300
# 532: 0.4763311 0.1782 4.2148 0.9864 0.5593 0.4057 0.1474 0.016 0.004 0.508
# 533: 0.5744769 0.2592 5.4060 0.9302 0.7010 0.4709 0.0374 0.012 0.004 0.304
# 534: 0.6375093 0.3192 6.9642 1.6955 0.7468 0.5443 0.1576 0.008 0.004 0.600
# 535: 0.5817449 0.2658 5.1730 1.0174 0.6401 0.5288 0.1292 0.008 0.004 0.536
# std_dev range size aspect elongation compactness transparency
# 1: 0.2313 0.904 0.83655 0.4373711 8.504961 3.381259 0.079812466
# 2: 0.2039 0.688 0.85420 0.5382676 6.097393 2.629685 0.046147976
# 3: 0.2178 0.724 0.97905 0.2519021 8.068804 3.244449 0.198187415
# 4: 0.1099 0.444 0.44115 0.2713256 4.891424 2.258683 0.180700941
# 5: 0.2682 0.840 0.93365 0.3766588 10.644316 4.054715 0.108440717
# ---
# 531: 0.0415 0.296 0.57860 0.5813064 19.787231 6.951178 0.035691352
# 532: 0.1477 0.504 0.48250 0.7253710 22.878484 7.932980 0.012785350
# 533: 0.0456 0.300 0.58595 0.6717546 26.149293 8.972371 0.019580367
# 534: 0.1903 0.596 0.64555 0.7288431 35.957843 12.091209 0.012455635
# 535: 0.1273 0.532 0.58445 0.8261209 23.125992 8.011616 0.004628539
# circularity density class
# 1: 0.2958 0.1690 Poecilostomatoïde
# 2: 0.3803 0.1607 Calanoïde
# 3: 0.3082 0.1606 Poecilostomatoïde
# 4: 0.4429 0.0157 Harpacticoïde
# 5: 0.2466 0.2020 Poecilostomatoïde
# ---
# 531: 0.1438 0.0080 Poecilostomatoïde
# 532: 0.1261 0.0263 Calanoïde
# 533: 0.1115 0.0097 Poecilostomatoïde
# 534: 0.0827 0.0503 Calanoïde
# 535: 0.1248 0.0344 Calanoïde# Réalisation du graphique
chart(data = copepoda, ~ class) +
geom_bar() +
xlab("Classe") +
ylab("Effectifs")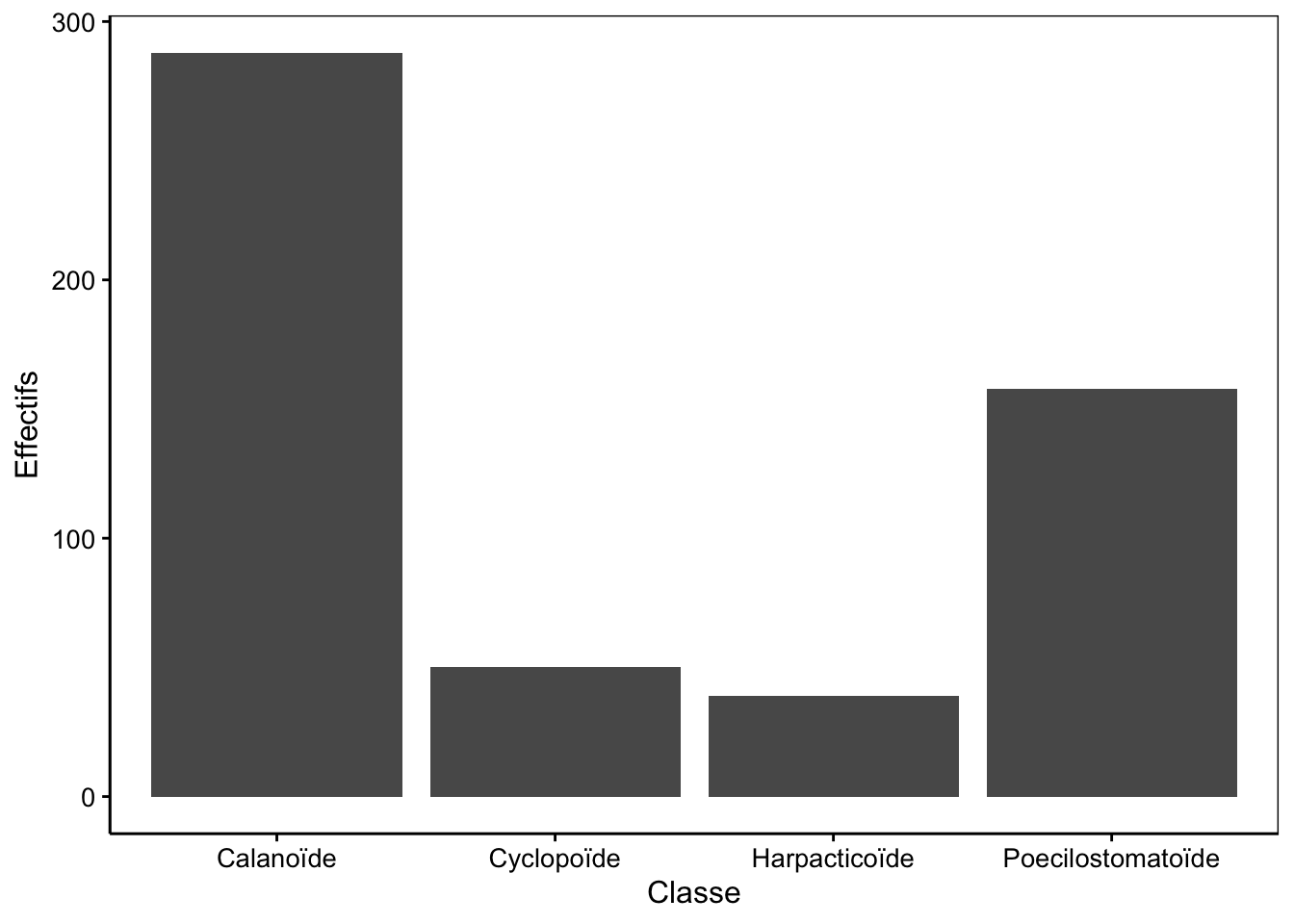
Figure 4.2: Abondances de quatres types de copépodes dans un échantillon de zooplancton.
La fonction geom_bar() se charge d’ajouter les barres verticales dans le graphique. La hauteur de ces barres correspond au nombre d’observations rencontrées dans le jeu de données pour chaque niveau (ou classe, ou groupe) de la variable facteur représentée.
4.1.2 Effectifs par deux facteurs
Reprenons maintenant le jeu de données biometry.
# Importation des données `biometry`
(biometry <- read("biometry", package = "BioDataScience", lang = "FR"))# gender day_birth weight height wrist year_measure age
# 1: H 1995-03-11 69.0 182 15.0 2013 18
# 2: H 1998-04-03 74.0 190 16.0 2013 15
# 3: H 1967-04-04 83.0 185 17.5 2013 46
# 4: H 1994-02-10 60.0 175 15.0 2013 19
# 5: F 1990-12-02 48.0 167 14.0 2013 23
# ---
# 391: H 1998-08-12 80.0 177 18.0 2017 19
# 392: F 1999-08-12 67.3 173 15.0 2017 18
# 393: H 1968-08-18 84.0 187 18.0 2017 49
# 394: F 1971-08-18 64.9 166 15.0 2017 46
# 395: H 1999-08-12 68.7 182 15.0 2017 18Nous voulons représenter des barres pour les effectifs d’hommes et de femmes dans ce jeu de données (variable gender), mais en les séparant par année (variable year_measure). C’est faisable, mais notez que, si gender est déjà une variable facteur <fct>, year_measure est encodé comme variable quantitative numérique (c’est un “double” indiqué <dbl>, c’est-à-dire un nombre décimal par opposition à entier <int>). Or nous devons absolument utiliser des variables facteur ici. Nous allons donc effectuer la conversion avec la fonction as.factor() avant de réaliser notre graphique en barres. Nous en profitons pour indiquer un label() en français pour cette variable.
# Conversion de la variable year_measure de numérique à facteur
biometry$year_measure <- as.factor(biometry$year_measure)
label(biometry$year_measure) <- "Année de la mesure"Notez bien comment on se réfère à la variable year_measure à l’intérieur du jeu de données biometry avec biometry$year_measure. Et cette notation peut aussi bien être utilisée pour récupérer la colonne year_measure dans un argument d’une fonction (à droite), que comme résultat de l’assignation (à gauche de l’opérateur d’assignation <-). Ainsi l’instruction qui transforme en facteur remplace la version dans le jeu de données biometry. Maintenant, considérons que nous nous intéressons aux mesures antérieures à 2017 (cela nous permettra d’illustrer des points importants relatifs à l’utilisation de variables facteurs).
Les variables facteurs sont encodées dans R comme des entiers 1, 2,
3, … pour les différents niveaux avec en plus, un attribut
levels qui y associe une description textuelle à chacun des
niveaux. Cela peut être perturbant quand la description textuelle est
constituée d’un nombre comme ici pour year_measure. Mais
les calculs sont prohibés sur les variables facteurs.
# Année de la mesure
# [1] 2017 2017 2017 2017 2017 2017
# Levels: 2013 2014 2016 2017Nous utilisons head() et tail() pour extraire les quelques lignes de début ou de fin d’un tableau. C’est utile pour en réduire la taille à l’impression. Faites très attention : lorsque vous imprimez le contenu d’une variable facteur, R substitue automatiquement les niveaux 1, 2, 3 … par le contenu textuel comme indiqué dans la dernière ligne Levels: ..., et l’imprime sans mettre le texte entre guillemets. Cela peut renforcer la fausse impression que c’est bien des valeurs numériques.
Vous commencez à comprendre que si vous effectuez maintenant la comparaison year_measure < 2017 lorsque cette variable est encodée comme facteur, cela ne fonctionnera pas comme vous le souhaitez ! Si on est chanceux, un message d’erreur ou d’avis (“warning”) est imprimé.
# Warning in Ops.factor(year_measure, 2017): '<' not meaningful for factorsNotez au passage que sfilter() n’utilise pas la notation biometry$year_measure, mais prend un premier argument qui est le jeu de données biometry, et la suite se réfère aux variables de ce jeu de données telles que year_measure en priorité aux autres variables disponibles dans l’environnement utilisateur de R. Aussi sfilter() renvoie tout le tableau remanié. Donc, nous devons l’affecter simplement à une variable qui contient ce tableau (biometry2 ici). Vous pouvez aussi utiliser la fonction filter() qui s’emploie de manière similaire.
Mais revenons à notre variable facteur. Dans d’autres cas, le résultat peut être dramatique, car le calcul est appliqué à l’encodage des niveaux de la variable facteur. Or, avec quatre niveaux, les encodages sont 1, 2, 3 et 4, … et ils sont bien évidemment tous inférieurs à 2017 (pour rappel, “2013”, “2014”, “2016” et “2017” sont les libellés textuels des niveaux de la variable facteur) !
De manière générale, n’effectuez jamais de calcul
sur des variables facteurs. Tranformez-les toujours avant. Si les
libellés contiennent des valeurs numériques sur lesquelles vous voulez
faire des calculs, utilisez
as.numeric(as.character(VARFACT)), et une fois le calcul
réalisé, retransformez en facteur avec as.factor().
Le calcul explicite et sûr est donc le suivant :
# Transforme de manière sûre factor -> numeric (double)
biometry$year_measure <- as.numeric(as.character(biometry$year_measure))
# Filtre les données sur une copie du tableau
biometry2 <- sfilter(biometry, year_measure < 2017)
# Retransforme en variable factor
biometry2$year_measure <- as.factor(biometry2$year_measure)
# Vérification
tail(biometry2)$year_measure# [1] 2016 2016 2016 2016 2016 2016
# Levels: 2013 2014 2016Naturellement ici, la bonne stratégie est d’effectuer le calcul sur le tableau de départ avant de transformer en facteur, mais nous sommes partis de la variable facteur à titre d’illustration d’un cas qui peut se rencontrer en pratique. À présent que nous avons notre jeu de données sans les individus de 2017, et les variables correctement encodées, nous pouvons aborder différentes représentations pour observer des dénombrements tenant compte de plusieurs variables facteurs. Par défaut, l’argument position = a pour valeur "stack" (donc, lorsque cet argument n’est pas précisé dans geom_bar(), les barres sont empilées par rapport à la seconde variable facteur).
a <- chart(data = biometry2, ~ gender) +
geom_bar() +
ylab("Effectifs")
b <- chart(data = biometry2, ~ gender %fill=% year_measure) +
geom_bar() +
ylab("Effectifs") +
scale_fill_viridis_d()
combine_charts(list(a, b), common.legend = TRUE)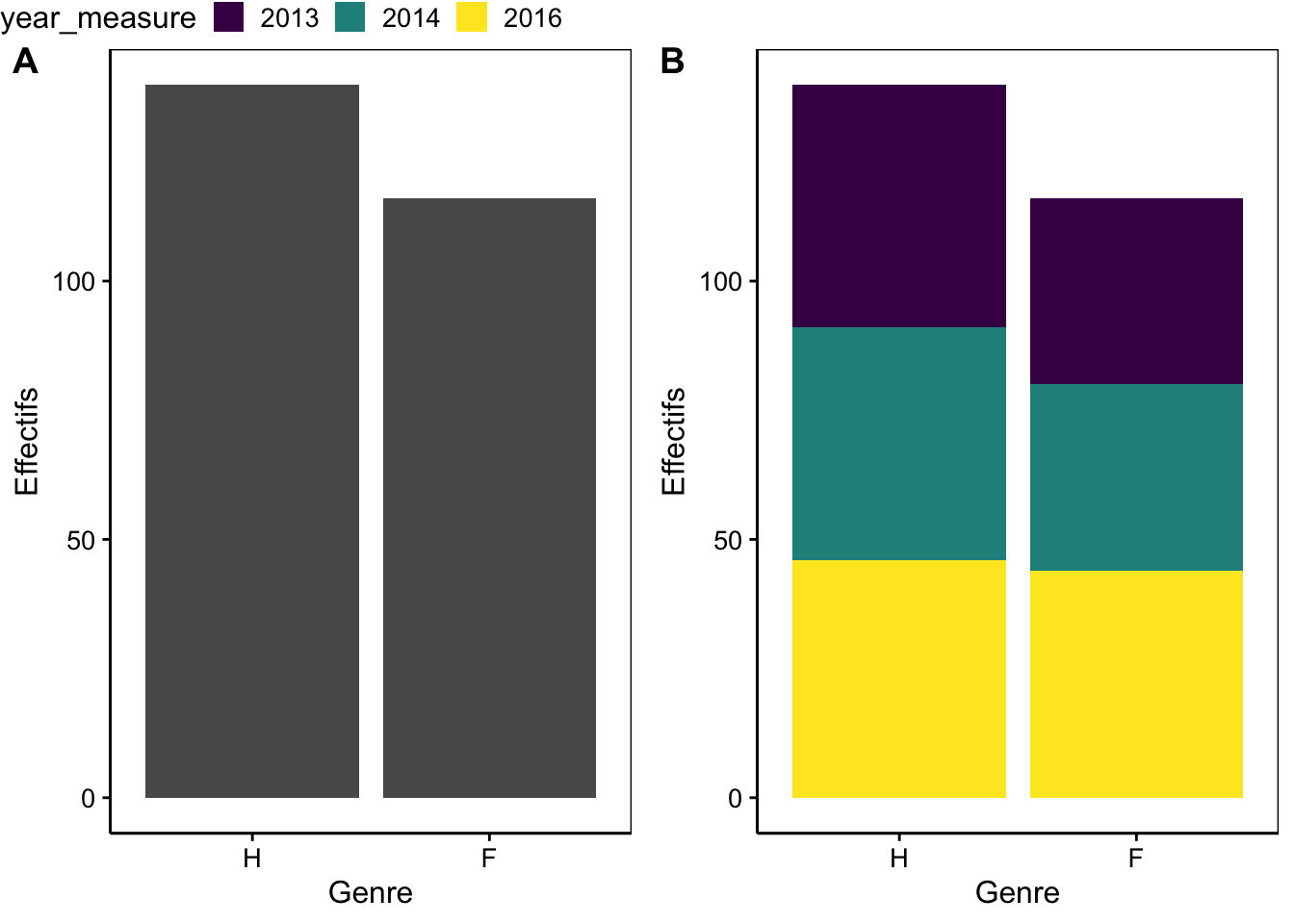
Figure 4.3: Dénombrement des hommes (H) et des femmes (F) dans l’étude sur l’obésité en Hainaut, (A) graphique utilisant un seul facteur. (B) graphique prenant en compte les années de mesure.
Il existe d’autres options en utilisant les valeurs "dodge" ou "fill" pour l’argument position =.
a <- chart(data = biometry2, ~ gender %fill=% year_measure) +
geom_bar(position = "stack") +
ylab("Effectifs") +
scale_fill_viridis_d()
b <- chart(data = biometry2, ~ gender %fill=% year_measure) +
geom_bar(position = "dodge") +
ylab("Effectifs") +
scale_fill_viridis_d()
c <- chart(data = biometry2, ~ gender %fill=% year_measure) +
geom_bar(position = "fill") +
ylab("Fractions") +
scale_fill_viridis_d()
combine_charts(list(a, b, c), common.legend = TRUE)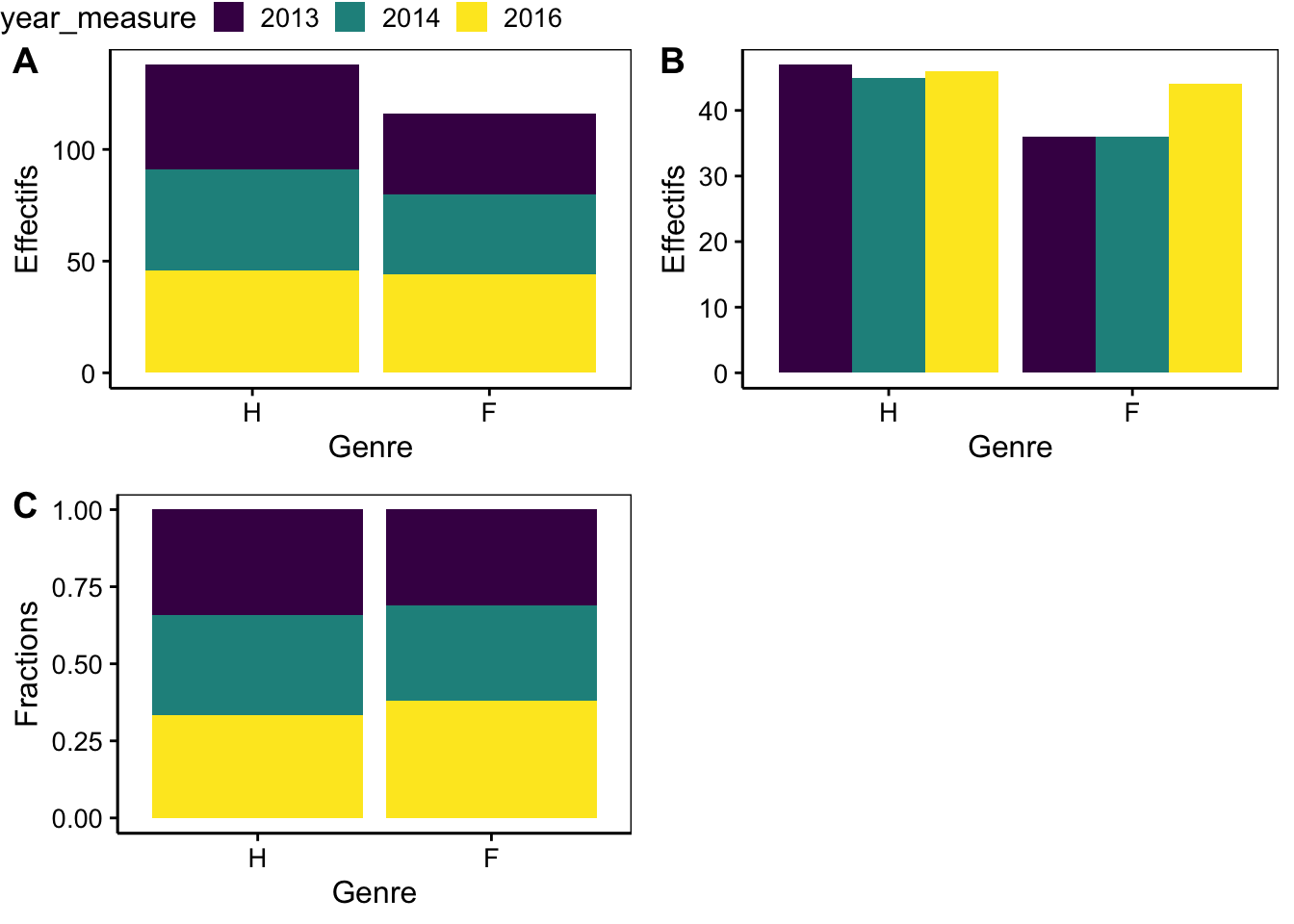
Figure 4.4: Dénombrement des hommes (H) et des femmes (F) dans l’étude sur l’obésité en Hainaut en tenant compte des années de mesure (différentes présentations).
Soyez vigilant à la différence entre l’argument position = "stack" (figure A) et position = "fill" (Figure C) qui malgré un rendu semblable ont l’axe des ordonnées qui diffèrent (dans le cas de "fill", il s’agit de la fraction par rapport au total qui est représentée, et non pas des effectifs absolus dénombrés).
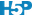
Pièges et astuces
Réordonner la variable facteur par fréquence
Vous pouvez avoir le souhait d’ordonner votre variable facteur afin d’améliorer le rendu visuel de votre graphique. Pour cela, vous pouvez employer la fonction fct_infreq().
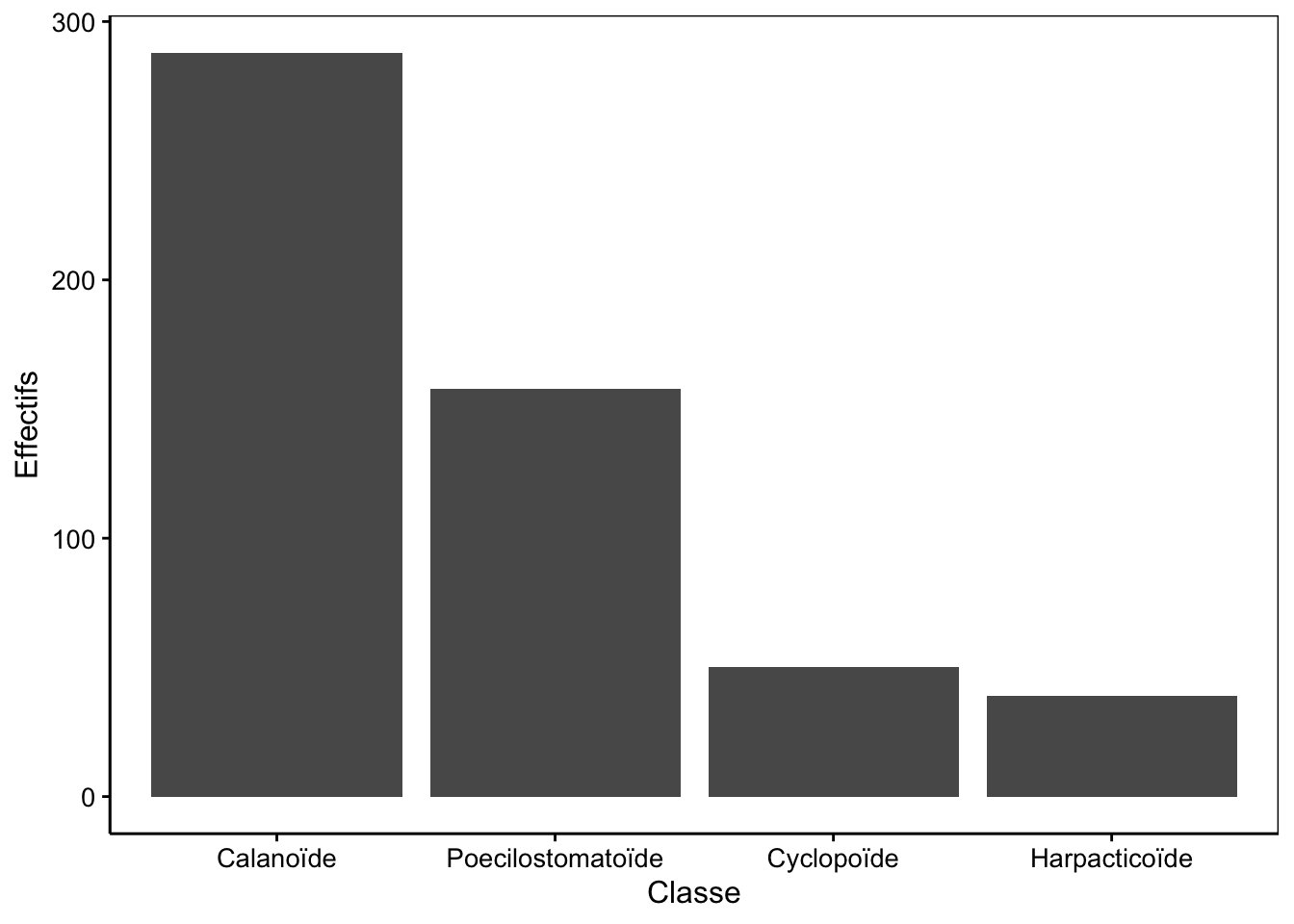
Figure 4.5: Dénombrement des classes de copépodes du jeu de données zooplankton.
Rotation des axes du graphique en barres
Lorsque les niveaux dans la variable étudiée sont trop nombreux, les légendes en abscisse risquent de se chevaucher, comme dans la Fig. 4.6
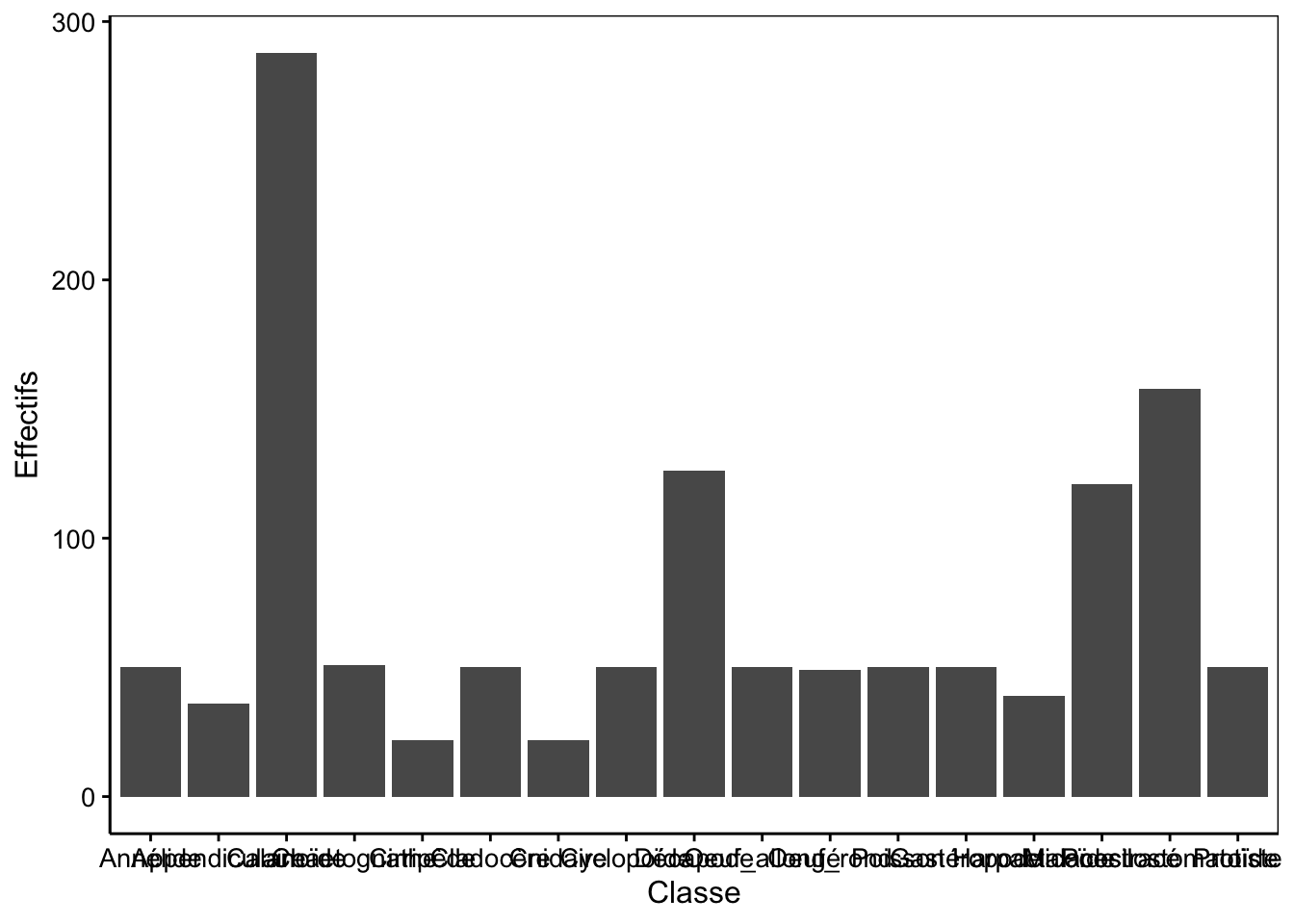
Figure 4.6: Dénombrement des classes du jeu de données zooplankton.
Dans ce cas, il est possible de réaliser un graphique en barres horizontales qui laisse plus de place pour le libellé sur l’axe. Il existe deux manières de le faire : préférentiellement en utilisant l’argument orientation = "y" de geom_bar() (mais alors il faut utiliser aes(y = ...) à la place de la formule). Une seconde option consiste à réaliser le graphique en barres verticales (tout le code reste identique), mais de rajouter coord_flip() tout à la fin. Utilisons successivement ces deux approches.
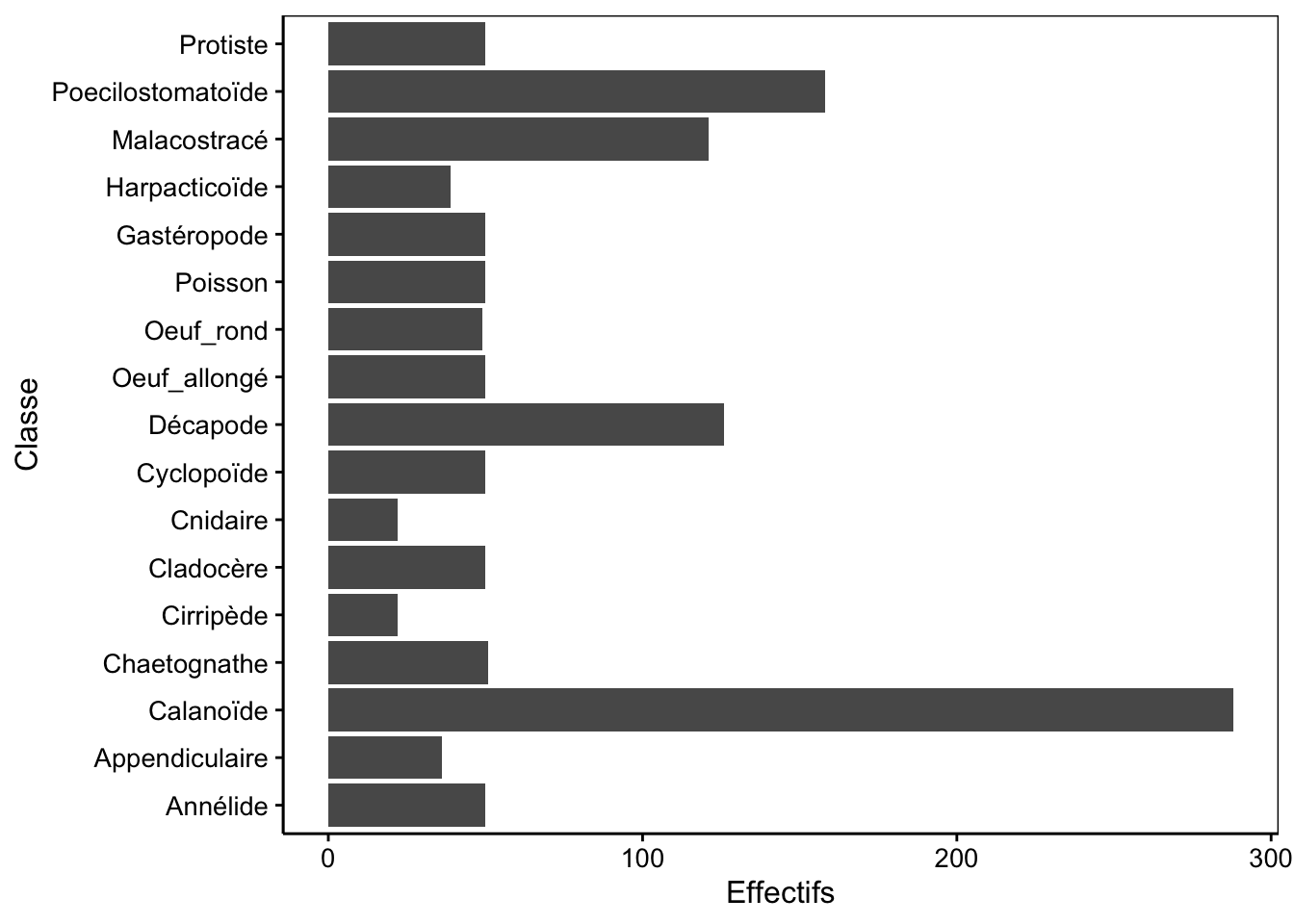
Figure 4.7: Dénombrement des classes du jeu de données zooplankton (version avec barres horizontales en utilisant orientation = "y").
Pourquoi ne peut-on pas utiliser de formule dans ce cas ? En fait, il faudrait écrire class ~, … seulement voilà, une formule ne peut pas avoir un membre de droite vide. Donc, on est dans une impasse et on doit utiliser la forme explicite aes() pour “aesthetics” en anglais qui indique quelle variable est utilisée pour quoi dans le graphique en indiquant y =.
Avec la fonction coord_flip() ajoutée à votre graphique, vous pouvez effectuer une rotation des axes (l’axe X devient Y et inversement) pour obtenir un graphique en barres horizontales. De plus, l’œil humain perçoit plus distinctement les différences de longueurs horizontales que verticales. Donc, de ce point de vue, le graphe en barres horizontales est considéré comme meilleur que le graphe en barres verticales.
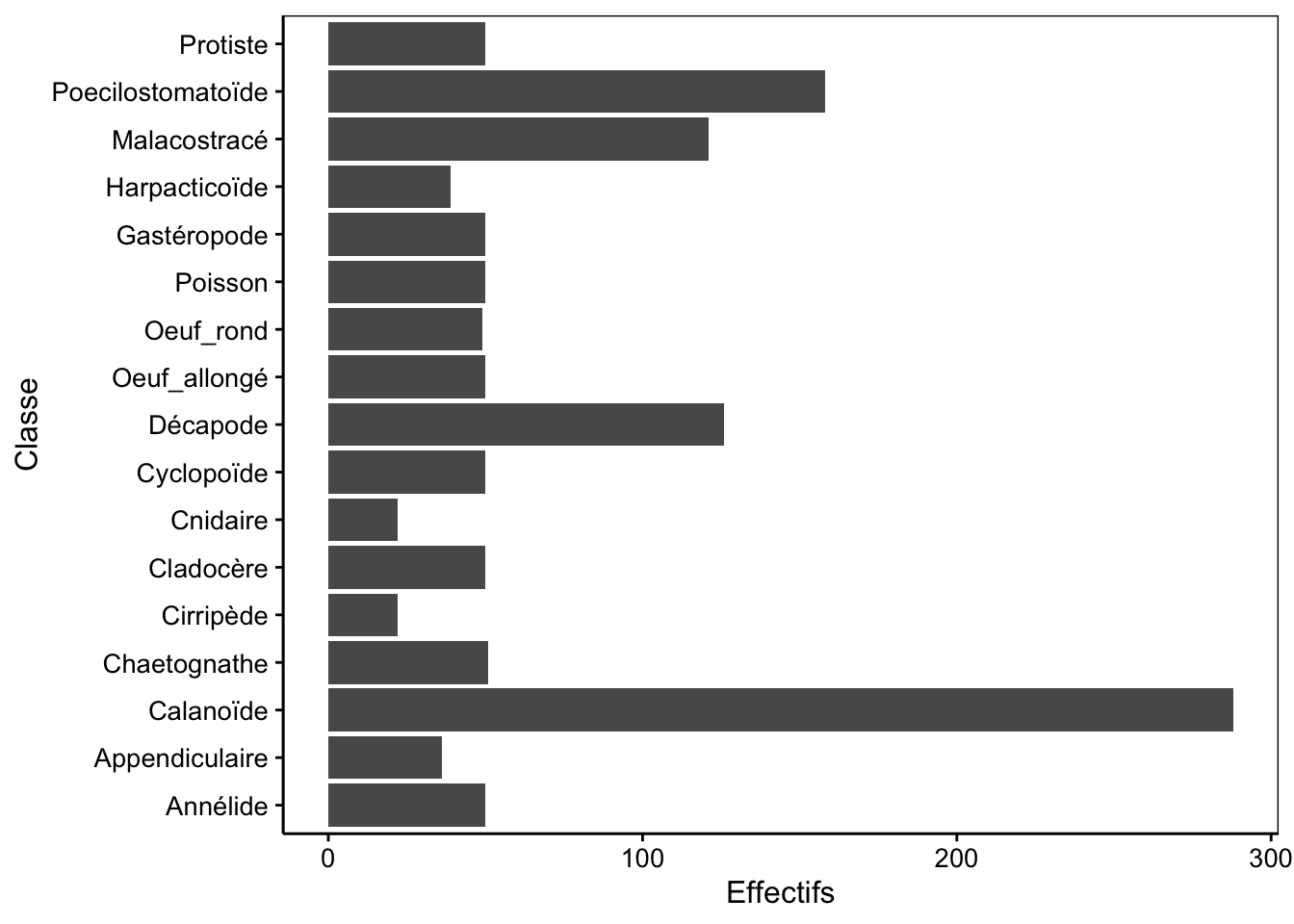
Figure 4.8: Dénombrement des classes du jeu de données zooplankton (version avec barres horizontales en utilisant coord_flip()).
Avec coord_flip(), gardez toujours à l’esprit que vos
axes finaux X et Y sont inversés avant l’utilisation de cette
instruction. Ainsi, si vous voulez changer le libellé de l’axes X sur le
graphique final, mais avant d’avoir indiqué
coord_flip(), c’est en fait le libellé de l’axe Y que vous
devez indiquer avec, par exemple ylab() comme c’est le cas
dans la figure précédente pour le libellé “Effectifs”.
Pour en savoir plus
Graphes en barres à l’aide de ggplot2. Un tutoriel en anglais utilisant la fonction
ggplot().Page d’aide de la fonction
geom_bar()en anglais.Une page qui présente l’utilisation de geom_col(), une autre fonction qui réalise des graphiques en bâtonnets, en français.
4.1.3 Valeurs moyennes
Le graphique en barres peut être aussi employé pour résumer des données numériques via la moyenne. Il ne s’agit plus de dénombrer les effectifs d’une variable facteur, mais de résumer des données numériques en fonction d’une variable facteur. On peut exprimer cette relation dans R sous la forme de :
\[y \sim x\]
que l’on peut lire :
\[y \ en \ fonction \ de \ x\]
Avec y une variable numérique et x une variable facteur. Considérez l’échantillon suivant :
1, 71, 55, 68, 78, 60, 83, 120, 82 ,53, 26Calculez la moyenne sur base de la formule de la moyenne
\[\overline{y} = \sum_{i = 1}^n \frac{y_i}{n}\]
# Création du vecteur
x <- c(1, 71, 55, 68, 78, 60, 83, 120, 82, 53, 26)
# Calcul de la moyenne
mean(x)# [1] 63.36364Les instructions pour produire ce graphe en barres à l’aide de chart() sont :
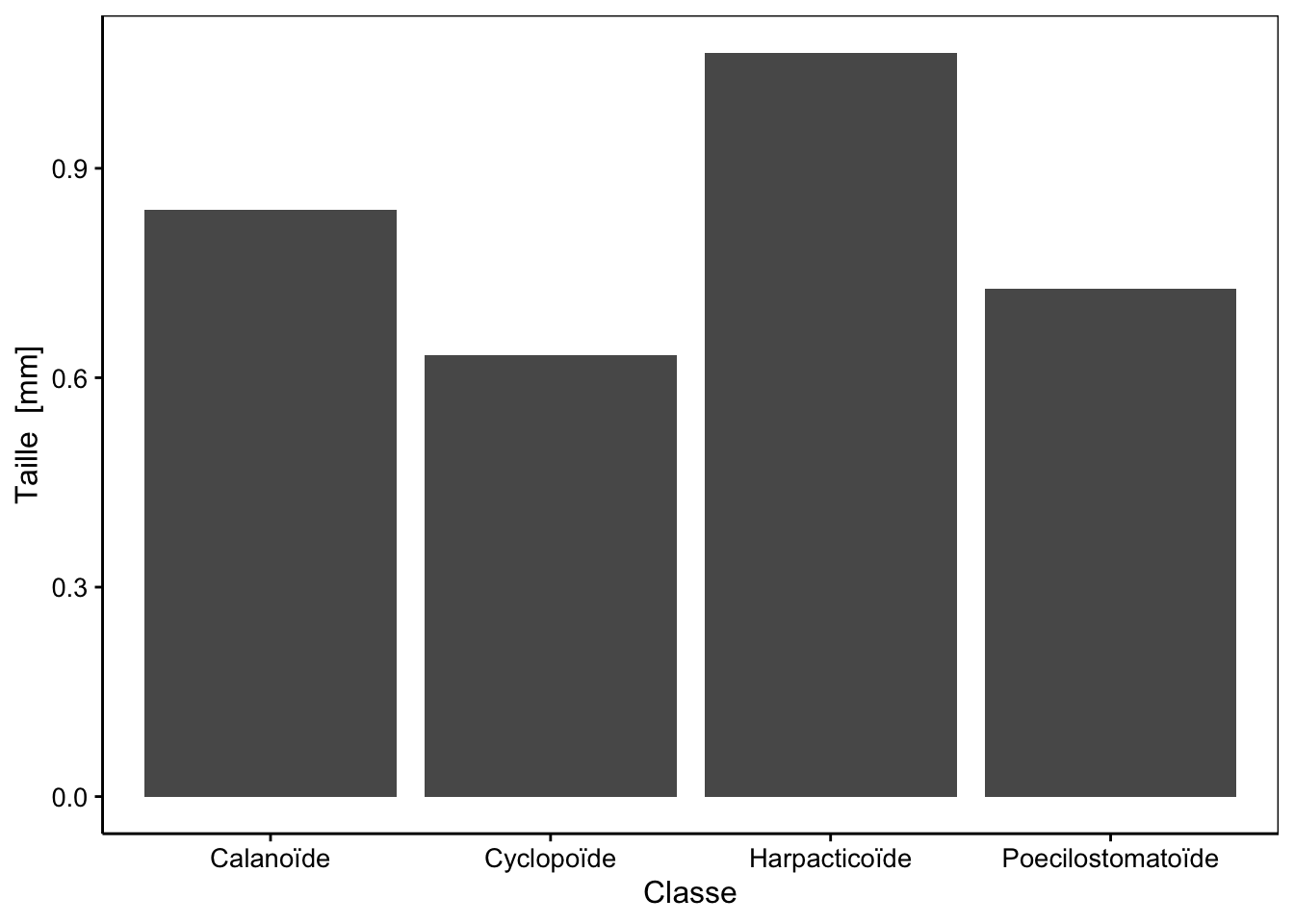
Figure 4.9: Exemple de graphique en barres représentant les moyennes de tailles par groupe zooplanctonique.
Ici, nous faisons appel à une autre famille de fonctions : celles qui effectuent des calculs sur les données avant de les représenter graphiquement. Leurs noms commencent toujours par stat_.
Le graphe en barres pour représenter les moyennes est très répandu dans le domaine scientifique malgré le grand nombre d’arguments en sa défaveur et que vous pouvez lire dans la section pour en savoir plus ci-dessous. L’un des arguments le plus important est la faible information qu’il véhicule puisque l’ensemble des données n’est plus représenté que par une valeur (la moyenne) pour chaque niveau de la variable facteur. Pour un petit nombre d’observations, il vaut mieux toutes les représenter à l’aide d’un nuage de points. Si le nombre d’observations devient très grand (dizaines ou plus), le graphique en boites de dispersion est plus indiqué (voir plus loin dans ce module). Le graphique en violon (cf. module précédent) est également utilisable s’il y a encore plus de données.
Pour en savoir plus
Beware of dynamite. Démonstration de l’impact d’un graphe en barres pour représenter la moyenne (et l’écart type) = graphique en “dynamite”.
Dynamite plots: unmitigated evil? Une autre comparaison du graphe en dynamite avec des représentations alternatives qui montre que le premier peut avoir quand même quelques avantages dans des situations particulières.