8.2 Test d’hypothèse

Le test d’hypothèse ou test statistique est l’outil le plus simple pour répondre à une question via l’inférence. Il s’agit ici de réduire la question à sa plus simple expression en la réduisant à deux hypothèses contradictoires (en gros, la réponse à la question est soit “oui”, soit “non” et rien d’autre).

L’hypothèse nulle, notée \(H_0\) est l’affirmation de base ou de référence que l’on cherchera à réfuter,
L’hypothèse alternative, notée \(H_1\) ou \(H_a\) représente une autre affirmation qui doit nécessairement être vraie si \(H_0\) est fausse.

Les deux hypothèses ne sont pas symétriques. Notre intention est de rejeter \(H_0\). Dans ce cas, nous pourrons considérer que \(H_1\) est vraie, avec un certain degré de certitude que nous pourrons également quantifier. Si nous n’y arrivons pas, nous dirons que nous ne pouvons pas rejeter \(H_0\), mais nous ne pourrons jamais dire que nous l’acceptons, car dans ce cas, deux explications resteront possibles : (1) \(H_0\) est effectivement vraie, ou (2) \(H_0\) est fausse mais nous n’avons pas assez de données à disposition pour le démontrer avec le niveau de certitude recherché.

À vous de jouer !

8.2.1 Becs croisés des sapins

Tout cela reste très abstrait. Prenons un exemple concret simple. Le bec-croisé des sapins Loxia curvirostra Linné 1758 est un passereau qui a la particularité d’avoir un bec dont les deux parties se croisent, ce qui donne un outil particulièrement adapté pour extraire les graines de conifères dont il se nourrit.

Bec-croisés des sapins mâles montrant les deux variétés (bec croisé à gauche ou à droite). Photo : Elaine R. Wilson (license CC BY-SA 3.0).

Comme des individus à bec croisé à gauche et d’autres à bec croisé à droite se rencontrent dans la même population, Groth (1992) a comptabilisé les deux types dans un échantillon aléatoire et représentatif de plus de 3000 oiseaux. Il a obtenu le tableau suivant :

(crossbill <- dtx(cb = c(rep("left", 1895), rep("right", 1752))))

# # A data.table: 3647 x 1
#    cb   
#    <chr>
#  1 left 
#  2 left 
#  3 left 
#  4 left 
#  5 left 
#  6 left 
#  7 left 
#  8 left 
#  9 left 
# 10 left 
# # … with 3,637 more rows

Ce tableau peut être résumé sous la forme d’un tableau de contingence :

(crossbill_tab <- table(crossbill$cb))

# 
#  left right 
#  1895  1752

Les scientifiques pensent que les variétés gauches et droites se rencontrent avec un ratio 1:1 dans la population étudiée suite à une sélection présumée basée sur le rapport des deux variétés. La question se traduit sous forme d’un test d’hypothèse comme ceci (retenez la notation particulière utilisée pour spécifier les hypothèses) :

\(H_0: \mathrm{P}(left) = \frac{1}{2}\ \mathrm{et}\ \mathrm{P}(right) = \frac{1}{2}\)
\(H_1: \mathrm{P}(left) \neq \frac{1}{2}\ \mathrm{ou}\ \mathrm{P}(right) \neq \frac{1}{2}\)

Pouvons-nous rejeter \(H_0\) ici ?

8.2.2 Test Chi² univarié

Le test Chi² (ou \(\chi^2\)) de Pearson est un test d’hypothèse qui permet de comparer des effectifs observés notés \(a_i\) à des effectifs théoriques \(\alpha_i\) sous l’hypothèse nulle pour les différents niveaux \(i\) allant de 1 à \(n\) d’une variable qualitative (version dite univariée du test). A noter que par rapport à la définition des hypothèses ci-dessus, ce ne sont pas les probabilités qui sont testées, mais les effectifs.

Conditions d’application

Tout test d’hypothèse impose des conditions d’application qu’il faudra vérifier avant d’effectuer le test. Pour le test \(\chi^2\), ce sont :

échantillonnage aléatoire et observations indépendantes,
aucun effectif théorique (ou probabilité) sous \(H_0\) nul,
aucun effectif observé, si possible, inférieur à 5 (ceci n’est pas une condition stricte ; le test sera “approximativement” bon dans le cas contraire).

Ces conditions d’application sont bien rencontrées ici.

Réalisation du test Chi² dans R

Dans R, le test du \(\chi^2\) est réalisé facilement à l’aide de la fonction chisq.test(). Voici ce que cela donne et comment on l’interprète :

chisq.test(crossbill_tab, p = c(left = 1/2, right = 1/2), rescale.p = FALSE)

# 
#   Chi-squared test for given probabilities
# 
# data:  crossbill_tab
# X-squared = 5.6071, df = 1, p-value = 0.01789

Le premier argument donné à chisq.test() est le tableau de contingence à une entrée indiquant les effectifs observés, ici crossbill_tab. L’argument p = est la liste des probabilités attendues sous \(H_0\) et dont la somme vaut un (il est également préférable de nommer les valeurs par rapport aux niveaux correspondants dans le tableau, ici left = et right =). On peut aussi donner les effectifs attendus, mais il faut alors préciser rescale.p = TRUE.

L’exécution de ce code nous donne un court rapport avec :

Un titre qui précise le test d’hypothèse effectué (test \(\chi^2\) avec des probabilités sous \(H_0\) fournies via l’argument p =)
Un rappel du tableau de contingence traité (crossbill_tab ici)
La dernière ligne qui indique le résultat du test. Les détails et explications concernant cette ligne sont développés ci-dessous. L’interprétation se fait en fonction de la valeur P (p-value = 0.01789). En fonction d’un seuil choisi avant de faire le test, et appelé seuil \(\alpha\). La décision est prise comme suit :
- Si la valeur P est inférieure à \(\alpha\), nous rejetons l’hypothèse \(H_0\), considérée comme trop peu probable,
- Si la valeur P est supérieure ou égale à \(\alpha\), nous ne rejetons pas \(H_0\), et considérons que notre échantillon ne nous permet pas de considérer cette hypothèse nulle comme suffisamment improbable (soit elle est effectivement correcte, soit l’effectif \(n\) de notre échantillon est insuffisant pour démontrer qu’elle ne l’est pas au seuil \(\alpha\) choisi).

Souvent en biologie, on choisi \(\alpha\) = 5%, mais dans les cas où nous souhaitons avoir plus de “certitude” dans notre réponse, nous pouvons aussi choisir un seuil plus restrictif de 1%, voire de 0,1%. Encore une fois, les explications sont détaillées ci-dessous.

Explications détaillées

Voici comment ce test se construit. Notre tableau de contingence à simple entrée crossbill_tab contient nos \(a_i\). Nous devons donc calculer quels sont les effectifs théoriques \(\alpha_i\). Le nombre total d’oiseaux observés est :

sum(crossbill_tab)

# [1] 3647

… et les effectifs attendus sous \(H_0\) sont :

(alpha_i <- c(left = sum(crossbill_tab)/2, right = sum(crossbill_tab)/2))

#   left  right 
# 1823.5 1823.5

Les hypothèses du test \(\chi^2\) univarié se définissent comme ceci :

\(H_0: a_i = \alpha_i\) pour tout \(i\)
\(H_1: a_i \neq \alpha_i\) pour au moins un \(i\)

Le principe de la statistique \(\chi^2\) consiste à sommer les écarts au carré par rapport aux \(\alpha_i\) de référence divisés par ces mêmes \(\alpha_i\) pour quantifier l’écart entre les valeurs observées et les valeurs théoriques. Donc :

\[\chi^2_\mathrm{obs} = \sum_{i=1}^n\frac{(a_i - \alpha_i)^2}{\alpha_i}\]

Notez que cette statistique prend la valeur nulle lorsque tous les \(a_i\) sont strictement égaux aux \(\alpha_i\). Dans tous les autres cas, des termes positifs (le carré de différences est toujours une valeur positive) apparaissent. Donc la statistique \(\chi^2\) est d’autant plus grande que les observations s’éloignent de la théorie.

Calculons \(\chi^2_\mathrm{obs}\) dans notre cas³² :

(chi2_obs <- sum((crossbill_tab - alpha_i)^2 / alpha_i))

# [1] 5.607074

Pour répondre à la question, il nous faut une loi de distribution statistique qui permette d’associer une probabilité au quantile \(\chi^2_\mathrm{obs}\) sous \(H_0\). C’est là que le statisticien Karl Pearson vient à notre secours. Il a, en effet, modélisé la distribution statistique du \(\chi^2\). La loi du même nom admet un seul paramètre, les degrés de liberté (ddl) qui sont égaux au nombre de niveaux de la variable facteur étudiée \(n\) moins un. Ici, ddl = 2 - 1 = 1. La Fig. 8.1 représente la densité de probabilité d’une loi \(\chi^2\) typique³³. C’est une distribution qui démarre à zéro, passe par un maximum et est asymptotique horizontale à \(+\infty\).

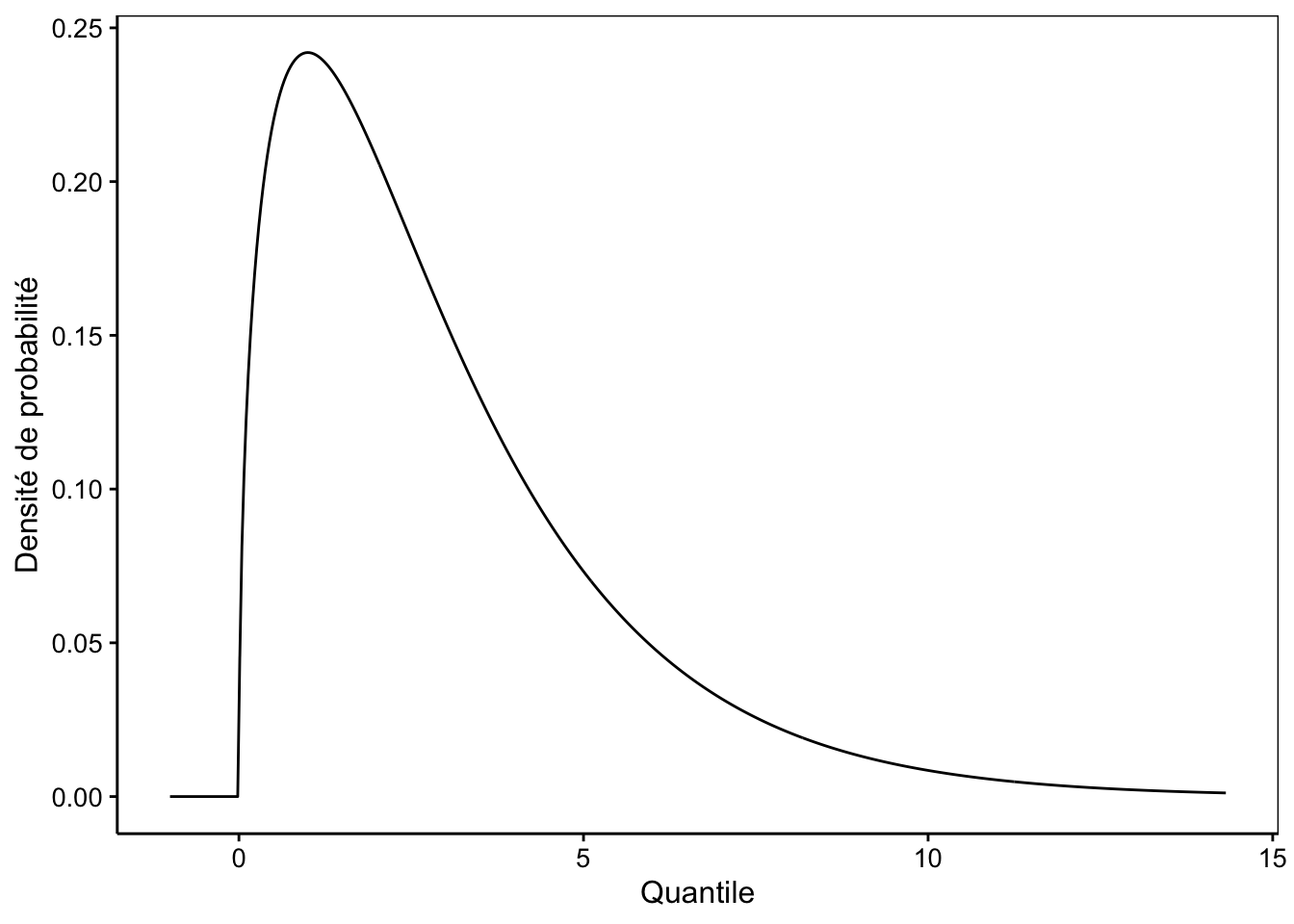
Allure typique de la densité de probabilité de la distribution Chi^2^ (ici ddl = 3).

Figure 8.1: Allure typique de la densité de probabilité de la distribution Chi² (ici ddl = 3).

8.2.3 Seuil α du test

Le raisonnement du test d’hypothèse pour répondre à notre question est le suivant. Connaissant la densité de probabilité théorique sous \(H_0\), nous savons que, plus le \(\chi^2_\mathrm{obs}\) est grand, moins il est plausible, car la densité de probabilité diminue. Nous devons décider d’une limite à partir de laquelle nous considérerons que la valeur observée est suffisamment grande pour que \(H_0\) devienne trop peu plausible et nous pourrons alors la rejeter. Cette limite se définit sous la forme d’une probabilité correspondant à une zone ou aire de rejet définie dans la distribution théorique de référence sous \(H_0\). Cette limite s’appelle le seuil \(\alpha\) du test.

Choix du seuil \(\alpha\) d’un test d’hypothèse. Le seuil \(\alpha\) est choisi avant de réaliser le test. Il est un savant compromis entre le risque de se tromper qui diminue plus \(\alpha\) est petit, et la possibilité d’obtenir le rejet de \(H_0\) lorsqu’elle est fausse qui augmentera avec \(\alpha\). Si on veut être absolument certain du résultat, on prend \(\alpha = 0\), mais dans ce cas on ne rejette jamais \(H_0\) et on ne tire donc jamais aucune conclusion utile. Donc, nous devons assouplir les règles et accepter un petit risque de se tromper. Généralement, les statisticiens choisissent \(\alpha\) = 5% dans les cas courants, et prennent 1%, ou même 0,1% dans les cas où il faut être plus strict (par exemple, si des vies dépendent du résultat). Nous pouvons nous baser sur ces références, même si nous verrons plus loin que cette pratique est de plus en plus remise en cause dans la littérature scientifique.

Poursuivons. Nous choisissons notre seuil \(\alpha\) = 5%. Cela définit l’aire la plus extrême de 5% à droite de la distribution \(\chi^2\) à 1 ddl comme zone de rejet (remplie en rouge sur la Fig. 8.2). Il nous suffit maintenant de voir où se place notre \(\chi^2_\mathrm{obs}\). S’il se situe dans la zone en rouge, nous rejetterons \(H_0\), sinon, nous ne la rejetterons pas.

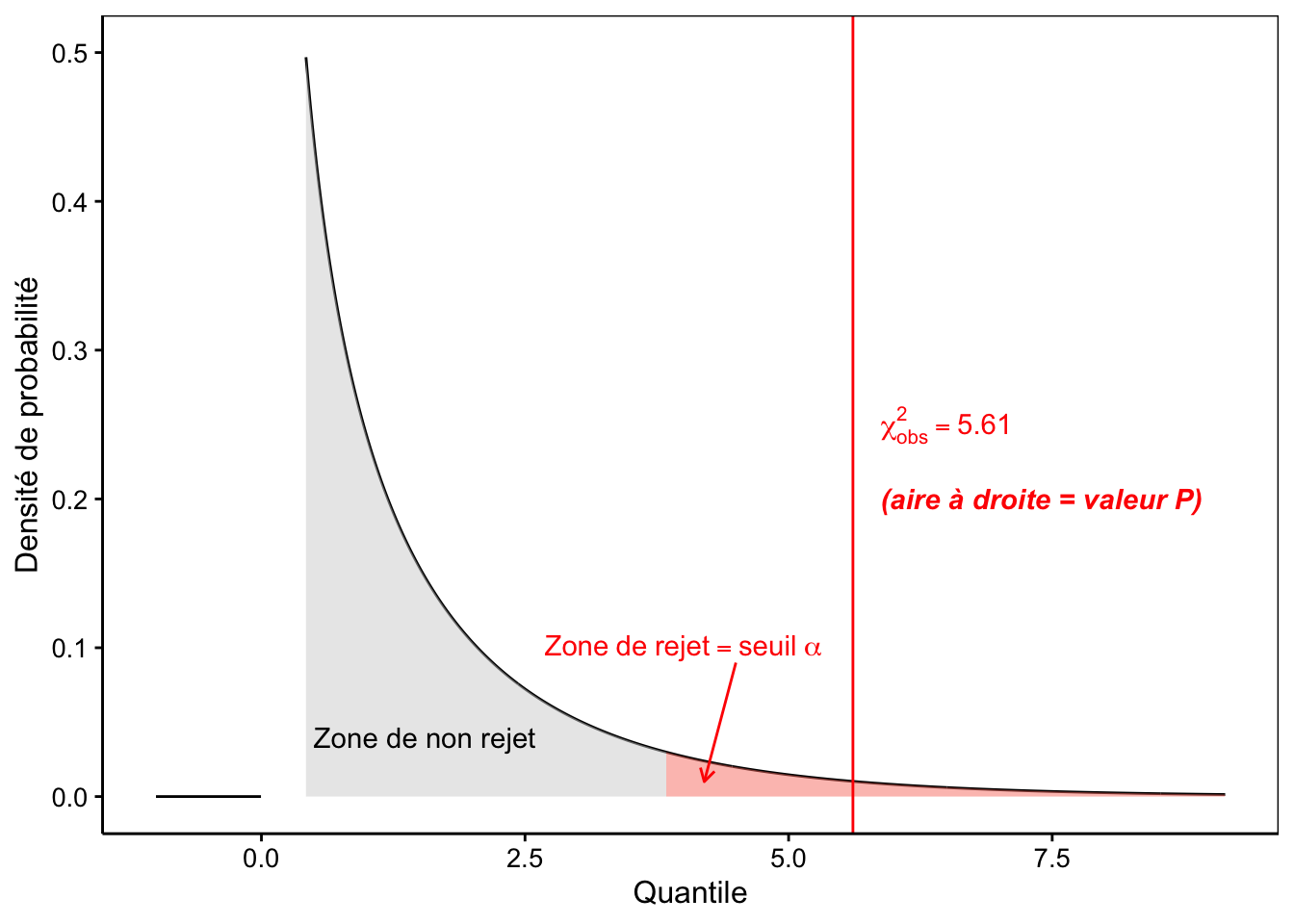
Densité de probabilité sous *H*~0~ (distribution Chi^2^ à 1 ddl), zone de rejet de 5% en rouge et position de la valeur observée (trait vertical rouge).

Figure 8.2: Densité de probabilité sous H₀ (distribution Chi² à 1 ddl), zone de rejet de 5% en rouge et position de la valeur observée (trait vertical rouge).

Où se situe la limite ? Nous pouvons facilement la calculer :

qchisq(0.05, df = 1, lower.tail = FALSE)

# [1] 3.841459

Notre \(\chi^2_\mathrm{obs}\) = 5,61 est plus grand que cette limite à 3,84 et se situe donc dans la zone de rejet de \(H_0\) du test. Nous rejetons donc \(H_0\) ici. Nous dirons que les becs-croisés à gauche sont significativement plus nombreux que ceux à droite au seuil \(\alpha\) de 5% (test \(\chi^2\) = 5,61, ddl = 1, valeur P = 0,018). Notez bien la façon particulière de reporter les résultats d’un test d’hypothèse !

Il nous manque encore juste un élément… qu’est-ce que cette “valeur P” de 0,018 reportée dans le résultat ? En fait, c’est la valeur de probabilité associée au test et correspond ici à l’aire à droite définie depuis le \(\chi^2_\mathrm{obs}\). Calculons-la :

pchisq(5.61, df = 1, lower.tail = FALSE)

# [1] 0.01785826

Le test d’hypothèse reporte la valeur P afin qu’un lecteur qui aurait choisi un autre seuil \(\alpha\) pourrait effectuer immédiatement sa propre comparaison sans devoir refaire les calculs. La règle est simple :

valeur P < seuil \(\alpha\), \(=> \mathrm{R}H_0\) (on rejette \(H_0\)),
valeur P ≥ seuil \(\alpha\), \(=> \rlap{\mathrm{R}} \diagup H_0\) (on ne rejette pas \(H_0\)).

À vous de jouer !

8.2.4 Effet de l’effectif étudié

En inférence, la qualité des données (échantillons représentatifs) est importante, mais la quantité aussi. Plus vous pourrez mesurer d’individus, mieux c’est. Par contre, dès que la taille de l’échantillon (ici, l’effectif total mesuré) est suffisante pour rejeter \(H_0\), vous n’avez plus besoin d’augmenter la taille de votre échantillon³⁴. Voyons l’effet de la taille de l’échantillon sur l’étude des becs-croisés des sapins. Nous n’avons pas besoin d’un effectif plus grand que celui mesuré, car nous rejetons \(H_0\) ici. Qu’aurait donné notre test \(\chi^2\), par contre, si l’auteur avait mesuré disons 10 fois moins d’oiseaux, les proportions restant par ailleurs identiques entre becs-croisés à gauche et à droite ?

# Proportions équivalentes, mais échantillon 10x plus petit
(crossbill_tab2 <- as.table(c(left = 190, right = 175)))

#  left right 
#   190   175

chisq.test(crossbill_tab2, p = c(left = 1/2, right = 1/2), rescale.p = FALSE)

# 
#   Chi-squared test for given probabilities
# 
# data:  crossbill_tab2
# X-squared = 0.61644, df = 1, p-value = 0.4324

Nous constatons que la valeur du \(\chi^2_{obs}\) dépend de l’effectif. Sa valeur est plus petite ici. Par conséquent, la valeur P a également changé et elle vaut à présent 43%. Cette valeur est supérieure maintenant à notre seuil \(\alpha\) de 5%. Donc, nous ne pouvons pas rejeter \(H_0\). Dans un pareil cas, nous conclurons que les becs-croisés à gauche ne sont pas significativement plus nombreux que ceux à droite au seuil \(\alpha\) de 5% (test \(\chi^2\) = 0,62, ddl = 1, valeur P = 0,43). Notez, c’est important, que nous n’avons pas écrit “ne sont pas”, mais nous avons précisé “ne sont pas significativement” plus nombreux. C’est un détail très important. En effet, cela veut dire que l’on ne peut pas conclure qu’il y ait des différences sur base de l’échantillon utilisé, mais il se peut aussi que l’échantillon ne soit pas suffisamment grand pour mettre en évidence une différence. Or, nous avons analysé en réalité un plus grand échantillon (crossbill), et nous savons bien que c’est effectivement le cas. Est-ce que vous saisissez bien ce que le mot significativement veut dire, et la subtilité qui apparaît lorsqu’un test d’hypothèse ne rejette pas \(H_0\) ? Les conclusions tirées avec crossbill et crossbill2 et le même test d’hypothèse sont diamétralement opposées, car l’une rejette et l’autre ne rejette pas \(H_0\). Pourtant ces deux analyses ne se contredisent pas ! Les deux interprétations sont simultanément correctes. C’est l’interprétation asymétrique du test qui permet cela, et l’adverbe significativement est indispensable pour introduire cette nuance dans le texte !

À vous de jouer !

Effectuez maintenant les exercices du tutoriel A08La_chi2 (Loi de distribution du Chi2 et test univarié).

BioDataScience1::run("A08La_chi2")

Réalisez le travail A08Ia_pea.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques I : inférence à l’UMONS à terminer avant le 2023-03-06 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md.

8.2.5 Test Chi² d’indépendance

Dans le cas d’un tableau de contingence à double entrée, qui croise les niveaux de deux variables qualitatives, nous pouvons effectuer également un test \(\chi^2\). Celui-ci sera calculé légèrement différemment et surtout, les hypothèses testées sont différentes.

Conditions d’application

Comme toujours, le test \(\chi^2\) d’indépendance est assortis de conditions d’application que nous devons vérifier avant de considérer d’utiliser ce test :

échantillon représentatif (échantillonnage aléatoire et individus indépendants les uns des autres),
attribution des traitements aux individus de manière aléatoire,
aucun effectif théorique nul,
Si possible, aucun effectif observé inférieur à 5 (pas règle stricte, mais voir à utiliser un test exact de Fisher ci-dessous dans la section “pour en savoir plus” en base de page dans ce cas).

Exemple et résolution dans R

Prenons le jeu de données concernant le test d’une molécule potentiellement anticancéreuse, le timolol :

(timolol <- dtx(
  traitement = c(
    rep("timolol", 160), rep("placebo", 147)),
  patient = c(
    rep("sain", 44), rep("malade", 116), 
    rep("sain", 19), rep("malade", 128))
  ))

# # A data.table: 307 x 2
#    traitement patient
#    <chr>      <chr>  
#  1 timolol    sain   
#  2 timolol    sain   
#  3 timolol    sain   
#  4 timolol    sain   
#  5 timolol    sain   
#  6 timolol    sain   
#  7 timolol    sain   
#  8 timolol    sain   
#  9 timolol    sain   
# 10 timolol    sain   
# # … with 297 more rows

Nous pouvons résumer ce tableau cas par variable en un tableau de contingence à double entrée :

(timolol_table <- table(timolol$traitement, timolol$patient))

#          
#           malade sain
#   placebo    128   19
#   timolol    116   44

Nous avons ici un tableau de contingence à double entrée qui répertorie le nombre de cas attribués aléatoirement au traitement avec placebo (somme de la première ligne, soit 128 + 19 = 147 patients) et le nombre de cas qui ont reçu du timolol sur la seconde ligne (116 + 44 = 160), tout autre traitement étant par ailleurs équivalent. Nous avons donc un total général de 307 patients étudiés. Les conditions d’application du test sont rencontrées ici.

La répartition dans le tableau selon les colonnes est, elle, tributaire des effets respectifs des deux traitements ? La clé ici est de considérer comme \(H_0\) un partitionnement des cas équivalents entre les deux traitements. Ceci revient au même que de dire que l’effet d’une variable (le traitement administré) est indépendant de l’effet de l’autre variable (le fait d’être guéri ou non). C’est pour cette raison qu’on parle de test \(\chi^2\) d’indépendance. Les hypothèses sont :

\(H_0:\) indépendance entre les deux variables
\(H_1:\) dépendance entre les deux variables

Toute la difficulté est de déterminer les \(\alpha_i\), les effectifs qui devraient être observés sous \(H_0\). Si le partitionnement était identique selon tous les niveaux des deux variables, nous aurions autant de cas dans chaque cellule du tableau, soit 307/4 = 76,75. Mais n’oublions pas que nous avons attribué plus de patients au traitement timolol qu’au traitement placebo. De même, nous ne contrôlons pas le taux de guérison de la maladie qui n’est d’ailleurs généralement pas d’un patient sur 2. Il faut donc pondérer les effectifs dans les lignes et les colonnes par rapport aux totaux dans les différents niveaux des variables (en ligne pour la variable traitement, en colonne pour la variable patient). Donc, si nous indiçons les lignes avec \(i = 1 ..m\) et les colonnes avec \(j = 1..n\), nos effectifs théoriques \(\alpha_{i,j}\) sous hypothèse d’indépendance entre les deux variables sont :

\[\alpha_{i, j} =\frac{total\ ligne_i \times total\ colonne_j}{total\ général}\]

Nous pouvons dès lors calculer le \(\chi^2_{obs}\) pratiquement comme d’habitude via :

\[\chi^2_{obs} = \sum_{i=1}^m{\sum_{j=1}^n{\frac{(a_{i,j} - \alpha_{i,j})^2}{\alpha_{i,j}}}}\]

Enfin, nous comparons cette valeur à la distribution théorique de \(\chi^2\) à \((m - 1) \times (n - 1)\) degrés de liberté. Dans le cas d’un tableau 2 par 2, nous avons \((2-1) \times (2-1) = 1\) degré de liberté. Voici le test effectué à l’aide de la fonction chisq.test() suivi de l’affichage des effectifs théoriques. Mais avant toute chose, nous devons choisir le seuil \(\alpha\) avant de réaliser le test. Nous prendrons ici, par exemple 1% puisque l’analyse est effectuée dans un contexte critique (maladie mortelle).

(chi2. <- chisq.test(timolol_table)); cat("Expected frequencies:\n"); chi2.[["expected"]]

# 
#   Pearson's Chi-squared test with Yates' continuity correction
# 
# data:  timolol_table
# X-squared = 9.1046, df = 1, p-value = 0.00255

# Expected frequencies:

#          
#             malade     sain
#   placebo 116.8339 30.16612
#   timolol 127.1661 32.83388

Interprétation

La valeur P de 0,0026 est inférieure au seuil \(\alpha\) choisi de 0,01. Donc, nous rejetons \(H_0\). Il n’y a pas indépendance entre les deux variables. Pour voir quels sont les effets de la dépendance entre les variables, nous devons comparer les effectifs théoriques affichés ci-dessus avec les effectifs observés. Dans le cas du placebo, sous \(H_0\), nous aurions du obtenir 117 malades contre 30 patients guéris. Or, nous en avons 128 malades et seulement 19 guéris. D’un autre côté, sous \(H_0\) nous aurions du observer 127 patients malades et 33 sains avec le timolol. Or, nous en observons 116 malades et 44 sains. Donc, les valeurs observées sont en faveur d’un meilleur effet avec le timolol. Nous pourrons dire : le timolol a un effet positif significatif sur la guérison de la maladie au seuil \(\alpha\) de 1% (\(\chi^2\) d’indépendance = 9,10, ddl = 1, valeur P = 0,0026).

Correction de Yates

Si nous calculons le \(\chi^2_{obs}\) à la main, nous obtenons :

alpha_ij <- chi2.[["expected"]]
# Les a_i,j sont dans timolol_table
sum((timolol_table - alpha_ij)^2 / alpha_ij)

# [1] 9.978202

Cela donne 9,98. Or notre test renvoie la valeur de 9,10. A quoi est due cette différence ? Lisez bien l’intitulé du test réalisé. Il s’agit de “Pearson’s Chi-squared test with Yates’ continuity correction”. Il s’agit d’une correction introduite par R dans le cas d’un tableau 2 par 2 uniquement et qui tient compte de ce que la distribution sous \(H_0\) est estimée à partir des mêmes données que celles utilisées pour le test, ce qui introduit un biais ainsi corrigé. Il est donc déconseillé de désactiver cette correction, même si nous pouvons le faire en indiquant correct = FALSE (ci-dessous, juste pour vérifier notre calcul du \(\chi^2_{obs}\) qui est maintenant identique, 9,98).

# Test d'indépendance sans correction de Yates
chisq.test(timolol_table, correct = FALSE)

# 
#   Pearson's Chi-squared test
# 
# data:  timolol_table
# X-squared = 9.9782, df = 1, p-value = 0.001584

À vous de jouer !

Effectuez maintenant les exercices du tutoriel A08Lb_chi2b (Test Chi2 d’indépendance).

BioDataScience1::run("A08Lb_chi2b")

8.2.6 Autres tests Chi²

Le test du \(\chi^2\) est également utilisé, dans sa forme univariée, pour comparer les effectifs observés par rapport à des effectifs théoriques suivant une loi de distribution discrète. Ce test s’appelle un test de qualité d’ajustement (“goodness-of-fit test” en anglais). Dans ce cas, le nombre de degrés de liberté est le nombre de catégories moins le nombre de paramètres de la distribution moins un.

Pour l’ajustement à une loi de distribution continue, il est possible de découper les données en classes et d’appliquer un test \(\chi^2\) dessus ensuite. Il existe cependant d’autres tests considérés comme plus efficaces dans ce cas, comme le test de Komogorov-Smirnov, notamment avec les corrections introduites par Lillefors. Pour l’ajustement à une distribution normale, des tests spécialisés existent comme le test de Shapiro-Wilk.

Gardez toujours à l’esprit que, quelle que soit la qualité d’un test d’ajustement, vous n’aurez jamais qu’une réponse binaire (oui ou non l’échantillon s’ajuste à telle distribution théorique). Les causes de dérive sont innombrables et seules des bonnes représentations graphiques (histogramme, graphe en violon, et surtout, graphique quantile-quantile) sont suffisamment riche en information pour explorer pourquoi et comment la distribution diffère d’une distribution théorique.

Pour en savoir plus

Le test de Chi2 avec R,
Le test G est considéré comme une bonne alternative dans certains cas (voir aussi Chi-square vs. G-test).
Le test exact de Fisher comme test alternatif, en particulier lorsque les effectifs sont faibles.

Faites également le calcul manuellement à la calculatrice pour vérifier que vous avez bien compris.↩︎
Les fonctions qui permettent les calculs relatifs à la distribution \(\chi^2\) dans R sont <x>chisq(). Leur utilisation est similaire à celle des distributions vues au module 7.↩︎
Attention ! Vous devez fixer la taille de l’échantillon dès le départ a priori. Vous ne pouvez pas accumuler des données jusqu’à obtenir un rejet de \(H_0\), sans quoi votre analyse sera biaisée.↩︎