6.2 Population et échantillonnage
Nos analyses statistiques seraient bien évidemment beaucoup plus simples si nous pouvions toujours mesurer tous les individus concernés par nos études. En fait, c’est presque toujours impossible, car les populations concernées sont souvent très larges, voire infinies. Nous devons donc mesurer un petit sous-ensemble de la population, ce que nous appelons un échantillon (sample en anglais) de taille finie déterminée (on parle de la taille de l’échantillon ou sample size en anglais). Le processus qui mène à la sélection des individus dans l’échantillon s’appelle l’échantillonnage (sampling en anglais). De cet échantillon, nous souhaitons malgré tout retirer un maximum d’information concernant la population d’origine. Cela s’appelle faire de l’inférence sur la population à partir de l’échantillon (to infer en anglais).
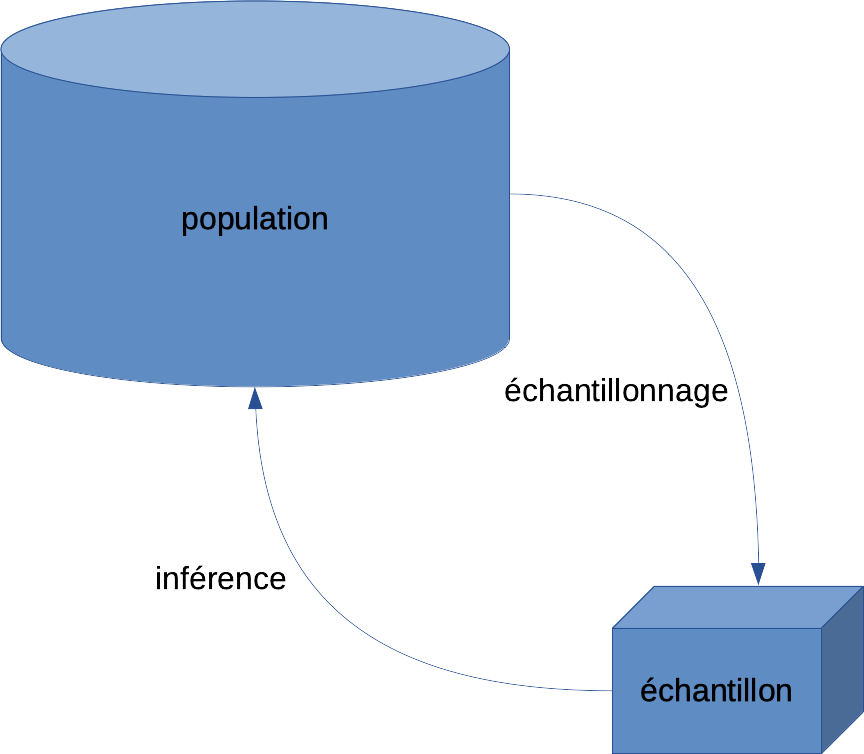
Faites attention à la signification des termes selon les disciplines. Par exemple, le terme population ne signifie pas la même chose pour un biologiste (ensemble des individus d’une même espèce pouvant se reproduire entre eux) et pour un statisticien (ensemble des valeurs que peut prendre une variable). Ainsi, la définition statistique du terme se réfère à un bien plus grand sous-ensemble en général. Par exemple, si nous étudions la souris Mus musculus, nous considérerons bien évidemment une population (ou une souche donnée pour les souris de laboratoire) en qualité de biologistes. Les statisticiens considéreront l’ensemble des souris qui existent, ont existé et existeront à l’avenir comme la population de souris.
De même, un individu statistique est une entité sur laquelle nous effectuons nos mesures (ce qui donne lieu à une observation pour chaque variable). Ainsi, un individu statistique peut correspondre ou non à un individu biologique selon ce que l’on considère. Par exemple, une section dans un organe peut constituer un individu statistique lors de l’étude de l’hétérogénéité à l’intérieur de cet organe. Nous aurons donc autant d’individus statistiques que de sites de prélèvement sur l’organe, … même si ce dernier provient au final du même individu biologique (même animal ou végétal) !
La variabilité tant au niveau de la population que de l’échantillon provient essentiellement de deux facteurs :
La variabilité individuelle inhérente (nous n’avons pas tous la même taille ni la même masse, par exemple),
Les erreurs de mesure.
Ces deux facteurs se cumulent pour contribuer à disperser les valeurs d’un individu à l’autre. Nous n’avons que peu de prise sur la variabilité individuelle, mais nous pouvons parfois réduire les erreurs de mesure si cela s’avère souhaitable en utilisant un appareil de mesure plus précis, par exemple. Quoi qu’il en soit, plus la variabilité est importante, plus la taille de l’échantillon devra également être grande pour conserver une bonne “représentativité” de la population.
Du point de vue de la notation mathématique, nous utiliserons une lettre latine majuscule en italique pour représenter une variable, par exemple, X. La taille de l’échantillon est souvent notée n. Les observations individuelles de la variable x pour les n individus de l’échantillon seront alors notées avec une lettre minuscule en italique assortie d’un indice compris entre 1 et n, donc, xi de manière générale avec l’indice i variant de 1 à n. Ainsi, x5 représente la cinquième observation pour la variable X dans notre échantillon, et xn est la dernière observation.
6.2.1 Échantillonnage aléatoire
La démarche du statisticien et du scientifique des données est de retirer un maximum d’information d’un échantillon afin de faire des inférences fiables sur la population tout entière (c’est-à-dire, tenter de tirer des conclusions les plus générales possibles à partir de l’étude d’un petit échantillon seulement). Ceci n’est possible que si l’échantillon “est conforme” à la population. En langage statistique on dit que l’échantillon est représentatif.
Un échantillon représentatif n’est pas facile à obtenir et il faut respecter scrupuleusement certaines règles pour l’obtenir. A contrario un échantillon non représentatif s’obtient sans précautions particulières, mais ce dernier est quasi toujours totalement inutile (on ne peut tirer de conclusions que sur cet échantillon particulier). Imaginez un soudage qui ne représente pas la population sondée… quel est son intérêt ? Il est nul !
La meilleure façon d’obtenir un échantillon représentatif est de réaliser un échantillonnage aléatoire. Dans ce cas, chaque individu de la population doit avoir la même chance d’être sélectionné dans l’échantillon. Nous parlons aussi d’échantillonnage au hasard. Vous devez bien réfléchir au processus qui va mener à la sélection des individus dans l’échantillon. Celui-ci doit comporter une étape qui fait intervenir le hasard.
“Choisir au hasard” ses individus en les prélevant au petit bonheur la chance en fonction de son humeur n’est pas une bonne approche. En effet, notre main qui saisira les individus à inclure dans l’échantillon aura tendance à prélever ceux qui sont plus facile à attraper ou plus proches, par exemple. Il peut s’agir d’individus moins vigoureux, moins réactifs, ou au contraire, moins peureux… Du coup, nous n’étudierions qu’une fraction de la population qui correspond à une caractéristique particulière (ceux qui sont faibles et peu réactifs, par exemple)
Une bonne sélection aléatoire doit faire intervenir le hasard (tirage au sort dans une urne, pile ou face, jet de dés, ou génération de nombres dits “pseudo-aléatoires” à l’aide d’un ordinateur). Par exemple, si vous avez un élevage de souris dans votre laboratoire, et que vous considérez cet élevage comme votre population, vous pouvez réaliser deux groupes (témoin et traitement) de cinq souris chacun de plusieurs façons :
-
Prendre dix souris dans les cages “au hasard”, et les répartir toujours “au hasard” entre les deux groupes. Ce type d’échantillonnage est incorrect. En effet, votre choix sera (inconsciemment) conditionné.
-
Donner un identifiant numérique unique à chacune de vos souris. Ensuite tirer deux fois cinq identifiants à partir d’une urne, ou effectuer ce même traitement virtuellement à l’aide d’un ordinateur. Dans ce cas, l’échantillonnage sera réellement aléatoire et correctement réalisé !
En pratique, nous pourrons utiliser la fonction sample() dans R. Elle permet de simuler facilement et rapidement le processus de tirage au hasard depuis une urne. Dans le cas de nos deux groupes de cinq souris à partir d’un élevage qui contient 213 animaux numérotés de 1 à 213 (identifiants uniques), nous ferons :
# [1] 47 201 36 92 212# [1] 137 20 22 103 81Ici, la sélection aléatoire (en réalité, on parle de “pseudo-aléatoire” pour ces nombres générés par un algorithme, mais qui ont des propriétés très similaires au hasard pur) nous indique que nous devrons aller chercher les souris n°15, 12, 102, 136 et 42 dans notre élevage pour notre groupe témoin, et les souris n°187, 108, 211, 68 et 49 pour le groupe traitement.
Dans le cas où un échantillonnage doit se faire avec replacement (l’équivalent de replacer une boule dans l’urne à chaque tirage au sort), nous pouvons indiquer l’argument replace = TRUE dans sample(). Donc, quelque chose comme sample(0:9, size = 50, replace = TRUE) pour échantillon les chiffres 0 à 9 au hasard cinquante fois avec remise (à chaque tirage chaque chiffre a même chance d’être tiré).
L’utilisation de sample() est pratique, mais cela rend le code non reproductible. En effet, à chaque fois, la fonction génère une série différente au hasard (c’est son rôle !) Toutefois, comme la série est pseudo-aléatoire, il est possible de régénérer la même série une seconde fois si on part du même point dans l’algorithme qui la calcule. Cela peut être réalisé à l’aide de set.seed(). Vous devez indiquer comme argument à cette dernière fonction un nombre aléatoire. Ce nombre représentera une position dans la séquence générée par l’algorithme de sorte que la série suivante obtenue à l’aide de sample() sera toujours la même. Voici comment cela fonctionne :
# [1] 9 8 5 1 6 3Naturellement, chaque fois que vous insérez set.seed() dans votre code, vous devez indiquer un nombre différent, lui-même choisi au hasard.
6.2.2 Échantillonnage stratifié
L’échantillonnage aléatoire n’est pas la seule stratégie correcte. L’échantillonnage stratifié consiste à diviser la population en sous-populations identifiables facilement (par exemple, séparer la population en fonction du sexe, ou de l’âge, voire des deux simultanément). Ensuite, un échantillonnage aléatoire est réalisé à l’intérieur de chaque sous-population pour un nombre déterminé d’individus, souvent le même. Cette approche plus complexe est utile si les sous-populations sont très mal balancées (une sous-population possède bien plus d’individus qu’une autre).
Par exemple, vous voulez comparer des prélèvements sanguins faits sur une population d’Européens hospitalisés dans le but de déterminer les critères qui permettent de diagnostiquer une infection nosocomiale24 rare. Les individus sont suivis en hôpital par définition et nous admettrons que l’on sait a priori s’ils sont atteints de la maladie ou non grâce à d’autres tests plus lourds et coûteux. La maladie est rare, heureusement. Sa prévalence n’est que de 1 cas sur 10.000.
Dans ce cas, si vous effectuez un échantillonnage aléatoire de 100 patients ou même de 1.000 patients hospitalisés, vous avez toutes les chances de ne pas inclure même un seul patient atteint de l’infection ! Ici l’échantillonnage stratifié est utile. Il consiste à séparer les patients en deux sous-populations : ceux qui sont atteints et les autres. Ensuite, vous décidez, par exemple, d’analyser 50 prélèvements sanguins dans chacune des deux sous-populations. Vous échantillonnez alors 50 patients aléatoirement comme nous l’avons fait plus haut pour nos souris, mais à l’intérieur de chaque sous-population. Au final, votre échantillon contiendra alors 50 patients infectés et 50 autres qui ne le sont pas. Cet échantillon est également représentatif (sauf, bien sûr, concernant la prévalence de l’infection).
Une infection nosocomiale est une infection contractée dans un hôpital.↩︎